Effect of particle size on the sorption of lead from water by different species of sawdust: Equilibrium and kinetic study

Abstract

Full Article

Effect of Particle Size on the Sorption of Lead from Water by Different Species of Sawdust: Equilibrium and Kinetic Study 

Chidozie Charles Nnaji * and Stephen Chinwike Emefu 

Both the effect of particle size and initial concentration on the adsorption of lead by sawdust of two timber species were investigated using batch experimental equilibrium and kinetic studies. A 100% lead removal efficiency was recorded for the optimum particle size of 1.18 mm for Pycnanthus angolensis and 0.85 mm for Khaya ivorensis at an initial lead concentration of 10 mg/L. Freundlich isotherm (0.83 ≤ R² ≤ 0.96 for Khaya ivorensis and 0.94 ≤ R² ≤ 1.0 for Pycnanthus angolensis) performed better than Langmuir and Temkin isotherms. The Dubinin-Radushkevich isotherm was used to ascertain the sorption mechanism. Mean sorption energy (12.48 kJ/mol for Pycnanthus angolensis and 13.42 kJ/mol for Khaya ivorensis) indicated that  adsorption was by ion exchange. The pseudo-first order kinetic model (0.96 ≤ R² ≤ 1.0 for Khaya ivorensis and 0.90 ≤ R² ≤ 1.0 Pycnanthus angolensis) performed better than others with respect to R² values, while the intraparticle diffusion model performed better than the other kinetic models with respect to absolute mean error (AME). 

Keywords: Adsorption; Kinetics; Water; Lead; Sawdust; Adsorbent; Activation

Contact information: Department of Civil Engineering, University of Nigeria, Nsukka, Enugu State, Nigeria; * Corresponding author: chidozie.nnaji@unn.edu.ng

INTRODUCTION

The best waste management practices require the minimization of waste generation, as well as effective and optimal recycling of waste. Sawdust, a by-product of timber sawing, has long been recognized as a suitable, low-cost adsorbent; however, large quantities of sawdust continue to be improperly disposed. In general, an adsorbent can be assumed as “low-cost” if it requires little processing, is abundant in nature, or is a by-product/waste material from industry (Baley et al. 1999). With the increasing quantities of toxic heavy metals in industrial effluents, sawdust can be effectively utilized in reducing the heavy metal concentration of these effluents to tolerable limits before discharge. Adsorption is an excellent and economical process to treat industrial waste effluents, offering significant advantages like low-cost, availability, profitability, ease of operation, and efficiency (Fayemiwo et al. 2013).  As noted by Bailey et al. (1999), abundantly available, low-cost adsorbent can be disposed after the first cycle of use, without need for the expensive process of regeneration. Apart from being in continuous supply and abundantly available, sawdust is a free resource in developing countries where it is constantly disposed along with municipal solid waste. Just like other carbon-based waste products, sawdust is mostly composed of lignin and cellulose as well as other polar poly functional groups like alcohols, aldehydes, ketones, carboxylate, phenols, and ethers that are able to bind heavy metals through the replacement of hydrogen ions with metal ions in solution or by donation of an electron pair to form complexes with the metal ion in solution (Bulut and Tez 2007; Begum and Alhaji 2013). The high lignin content of sawdust makes it an excellent adsorbent for metals (Byrant et al. 1992; Argun et al. 2007). Moreover, sawdust contains different functional groups that take part in and increase adsorption capacity (Gad et al. 2013). Sawdust has optimal adsorption properties and can be employed in large-scale removal of contaminants from water (Mane et al. 2007; Kalavathy et al. 2009; Naiya et al. 2009). The removal of heavy metals by adsorption is preferable to other techniques such as precipitation, ion exchange, adsorption, filtration, electrodeposition, and reverse osmosis both in terms of economy and efficiency. Pal and Kuar (2013) observed that activated carbon made from sawdust of Dalbergia sissoo removed about 85% of hexavalent chromium from water. Gad et al. (2013) recorded up to 78% adsorption of lead by sawdust within 40 min of contact. Raji et al. (1997) employed activated sawdust in the adsorption of Pb (II), Hg (II), and Cd (II) and recorded very high adsorption efficiencies of 98.6%, 97.2%, and 95.1%, respectively. Fayemiwo et al. (2013) observed that activated sawdust performed much better than activated rice husk in the treatment of hospital effluent.

This study ascertained the effects of timber species and particle sizes on the adsorption of lead by activated sawdust. Maharani et al. (2010) reported that mill type and particle size affected the properties of sawdust. Two timber species (Pycanthus angolensis, commonly known as Akwa mmiri, and Khaya ivorensis, commonly known as mahogany) were selected because of their abundance and prevalence of use in woodworks. The timber species have very different characteristics. 

EXPERIMENTAL 

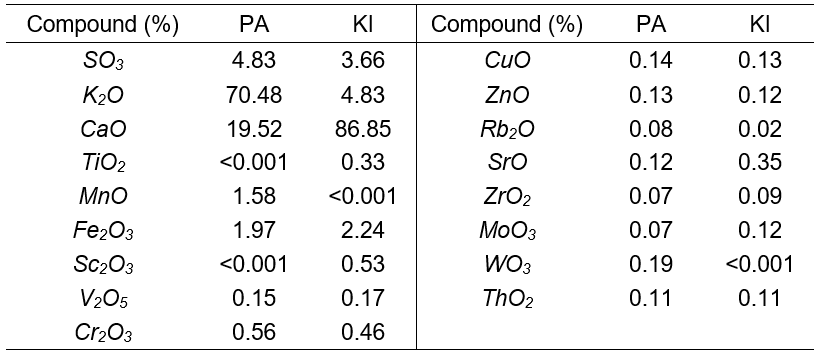
The two sawdust samples were obtained from a timber mill in the Enugu Timber Market. The sawdust samples were sieved into different sizes, and the particle size distributions were obtained. Khaya ivorensis had more fine particles than Pycnanthus angolensis. The sizes of Pycnanthus angolensis sawdust used were 2.36 mm, 2.00 mm, 1.18 mm, 0.71 mm, and 0.60 mm, which were denoted as PA (2.36 mm), PA (2.00 mm), PA (1.18 mm), PA (0.71 mm), and PA (0.60 mm), respectively. The sizes of Khaya Ivorensis sawdust used were 2.00 mm, 1.18 mm, 0.85 mm, 0.60 mm, and 0.30 mm, also denoted as KI (2.00 mm), KI (1.18 mm), KI (0.85 mm), KI (0.60 mm), and KI (0.30 mm), respectively. The pseudonyms were conceived such that the letters corresponded to the first letter of the name of the wood and the accompanying numbers corresponded to the standard BS sieve numbers. The slight variation in particle sizes used was a result of the different ranges of particle sizes between Khaya ivorensis and Pycnanthus angolensis. Table 1 shows the standard sieves used and their corresponding apertures. These samples were carbonized in the oven at a temperature of 250 °C, activated by mixing with 0.5 mol HCl, and soaked for 2 h. The slurry was repeatedly washed with deionized water until neutral pH was reached. It was then oven dried for 3 h at 103 °C to yield dried activated sawdust. Samples of Khaya ivorensis and Pycnanthus angolensis were sent to the Centre for Minerals Research and Development, Kaduna for chemical characterization by X-ray fluorescence examination. The internal structures of the raw and activated sawdust particles were examined using a Phenom Pro X, MVE016477830 scanning electron microscope (SEM) at the National Geosciences Research Laboratory Kaduna, Nigeria. The samples were mounted on sample stub using double adhesive. Samples were then coated with 5 nM of gold and then charged into the SEM column where they were viewed with a NavCam at an accelerating current of 10 kV.

Table 1. Sieve Sizes

Lead solutions of concentrations 130 mg/L, 110 mg/L, 90 mg/L, 70 mg/L, 50 mg/l, 30 mg/L, and 10 mg/L were prepared by adding 13 mL, 11 mL, 9 mL, 7 mL, 5 mL, 3 mL, and 1 mL of stock lead solution (1000 mg/L) into 100 mL of deionized water. A total of 200 mg of adsorbent was added to the lead solution. The mixture was agitated for 3 h. The concentration of lead remaining in solution after 3 h was determined using a UV spectrophotometer (UV-1800 Shimadzu, Tokyo, Japan) at a wavelength of 294 nm. The same procedure was repeated for all particle sizes of the activated sawdust made from the two timber species. The UV spectrophotometer was calibrated by determining the absorbance for predetermined concentrations of lead solution.  All equipment and reagents used were sourced from the National Centre for Energy Research and Development. The quantity of lead adsorbed, q_e, (mg/g), at time (t) was calculated by Eq. 1,

where C₀ and C_e were the initial and final lead concentration (mg/L), respectively. V is the volume of the adsorbate, and m is the mass of the adsorbent. The percentage of the lead ion removed from solution was calculated by Eq. 2. The percentage adsorption data were used to determine the optimum particle sizes for the sawdust from the two timber species. In order to ascertain whether the various particle sizes had significant effect on the sorption of lead by the two sawdust species, analysis of variance (ANOVA) was performed. The effect of initial concentrations of lead on sorption efficiency was also ascertained by ANOVA. The test was conducted at 95% confidence level using Microsoft Excel 2016.

Removal efficiency 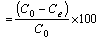                                                              (2)

The particle size with the highest removal efficiency for each of the timber species was selected for batch kinetic experiments. The rate of adsorption of a molecule unto a surface is an essential parameter when designing batch sorption systems; consequently, it is essential to establish the time dependence of such systems under various process conditions.

The sorption kinetics were investigated using various levels of lead concentration: low concentration (10 mg/L), medium concentration (50 and 70 mg/L), and high concentration (130 mg/L). Two hundred mg (0.2 g) of adsorbent was introduced into the lead solution and agitated. Samples of the adsorbate were taken at 1 min, 5 min, 10 min, 20 min, 40 min, 60 min, 180 min, and 240 min for determination of the sorption rate. To determine the sorption rate and appropriate sorption kinetics, five kinetic models were applied to the experimental data.

The performance of the kinetic models was evaluated using R² values and absolute mean error values. 

RESULTS AND DISCUSSION

The particle distributions of Pycnanthus angolensis and Khaya ivorensis are presented in Fig. 1. It can be seen that the curve for Pycnanthus angolensis lies above that of Khaya ivorensis for smaller particle sizes. This implies that Pycnanthus angolensis has a higher proportion of finer grains in this region. On the other hand, the curve of particle size distribution for Khaya ivorensis lies above that of Pycnanthus angolensis for larger particle sizes. Hence, Pycnanthus angolensis had more coarse particles than Khaya ivorensis. The vertical arrowed line demarcates the zone where Pycnanthus angolensis has more particles from the zone where Khaya ivorensis has more particles. Khaya ivorensis is harder and offers more resistance during sawing, thereby producing finer particles. Table 2 gives the chemical composition of the two sawdust species.

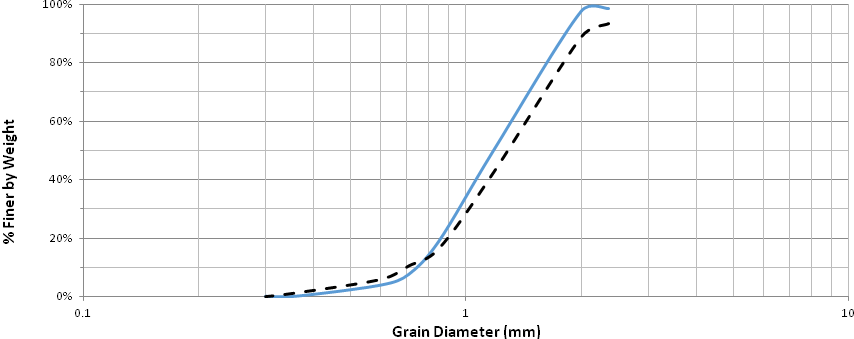
Fig. 1. Particle size analysis for Pycnanthus angolensis and Khaya ivorensis

Table 2. Chemical Composition of Pycnanthus angolensis and Khaya ivorensis sawdust

For Khaya ivorensis, the adsorption efficiency slightly increased as particle size increased from 0.3 mm to 2.0 mm for initial lead concentrations of 50 to 130 mg/L. However, for the low initial concentration of lead (10 to 30 mg/L), the adsorption efficiency increased from 48% for 30 mg/L to 79.4% and 100%, respectively, at an optimum particle size of 0.85 mm (Fig. 2). The trend was slightly different for Pycnanthus angolensis, which had an optimum particle size of 1.18 mm for the entire range of initial lead concentration studied.

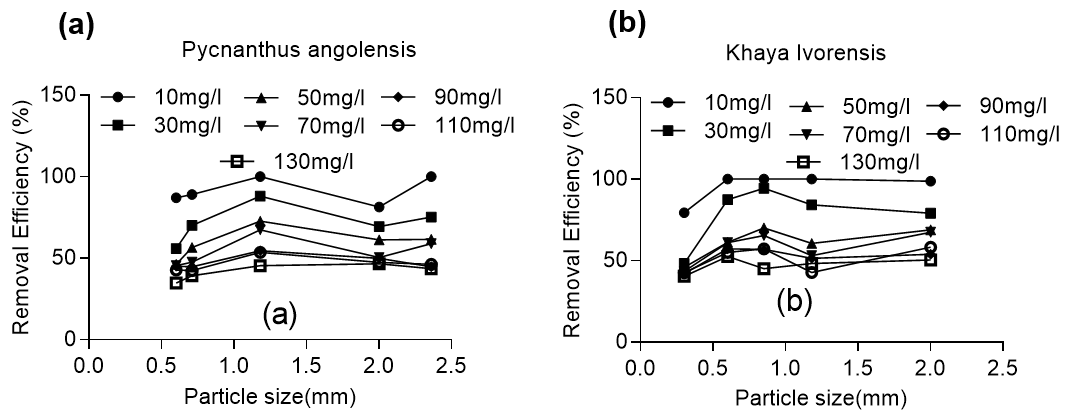
Fig. 2.  Effect of particle size on lead removal by (a) Pycnanthus angolensis and (b) Khaya ivorensis 

The highest adsorption efficiency obtained was 100% at particle sizes of 1.18 mm, 0.85 mm, and 0.6 mm initial lead concentration of 10 mg/L for Khaya ivorensis. An adsorption efficiency of 100% with particle sizes of 2.36 mm and 1.18 mm and a lead concentration of 10 mg/L was also obtained for Pycnanthus angolensis. A pairwise comparison of the removal efficiency based on particle size shows that Khaya ivorensis performed better than Pycnanthus angolensis particles of 2.0 mm and 0.6 mm for all concentrations of lead studied. However, Pycnanthus angolensis performed slightly better than Khaya ivorensis at a particle size of 1.18 mm for lead concentrations ranging from 30 to 130 mg/L (Fig. 3).

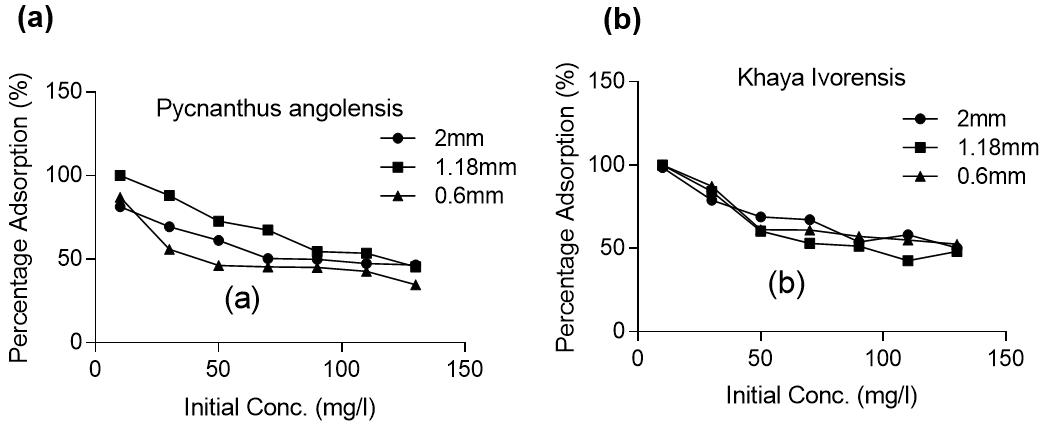
Fig. 3. Effect of initial concentrations on lead removal by (a) Pycnantthus angolensis and (b) Khaya ivorensis

Figure 3 shows that adsorption efficiency was reduced drastically from 10 mg/L to 130 mg/L with decreased initial lead concentration. This reduction in efficiency was attributed to the competition for limited active adsorption sites by numerous metal ions. Increasing the initial lead concentration from 10 mg/L to 130 mg/L approximately halved the efficiency of adsorption. However, it would be incorrect to judge the performance of the adsorbents solely based on removal efficiency because a greater quantity of lead was removed per gram of adsorbent at higher initial concentrations of lead. Further analysis showed that increasing the initial concentration of lead from 10 mg/L to 130 mg/L resulted in an increase of the quantity of lead adsorbed from 2.5 mg/g to 16.74 mg/g for Pycnanthus angolensis and from 2.5 to 15.21 mg/g for Khaya ivorensis. Under the same conditions, the adsorption efficiency was reduced from 100% to 43.5% for Pycnanthus angolensis and from 98.6% to 50.34% for Khaya ivorensis (Fig. 4). Increasing the initial lead concentration from 10 to 130 mg/L halved the removal efficiency but resulted in over a six-fold increase in the quantity of solute removed from the liquid phase (Fig. 4). Therefore, the reduction in adsorption efficiency with increase in the initial concentration of lead does not indicate a reduction in the adsorption potential but saturation and subsequent unavailability of active sites as a result of solute overdose.

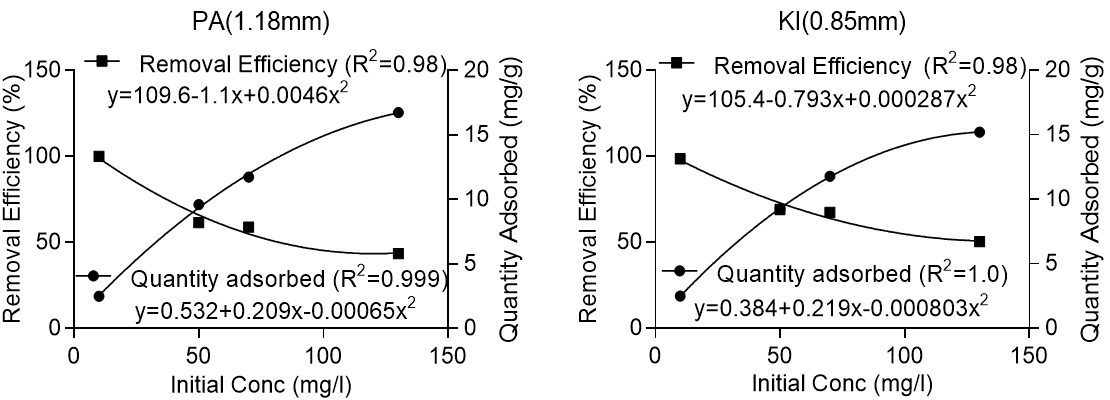
Fig. 4. Variation of removal efficiency and quantity adsorbed with initial concentration

Results of analysis of variance (Tables 3 and 4) show that both particle size and solute concentration had a very significant effect on the lead removal efficiency. However, the effect of the initial solute concentration far outweighed that of particle size. The effect of initial solute concentration was three times that of particle size for Khaya ivorensis and five times for Pycnanthus angolensis. This shows that the effect of initial concentration was more pronounced in Pycnanthus angolensis than in Khaya ivorensis. 

Table 3. Analysis of Variance for Removal Efficiency (Pycanthus angolensis)

Table 4. Analysis of Variance for Removal Efficiency (Khaya ivorensis)

Equilibrium studies that yield the capacity of the adsorbent and equilibrium relationships between adsorbent and adsorbate are described by adsorption isotherms that are usually the ratio between the quantity adsorbed and the remaining amount in solution at a fixed temperature in equilibrium. Adsorption mechanisms are usually described by isotherms that describe how the solute is distributed between the solid and liquid phases. The results of the adsorption experiment were fitted to Langmuir, Freundlich, and Temkin isotherms, in order to determine the adsorption process. The Dubinin-Radushkevich isotherm was also employed to ascertain the nature of the sorption process.

The Langmuir isotherm is used to describe monolayer sorption on the surface of a solid made up of elementary sites, each of which can adsorb one sorbate molecule (Hubbe et al. (2011). The Langmuir isotherm is based on the assumptions that (i) all adsorption sites are equivalent, (ii) a monolayer is formed and adsorbed molecules do not deposit on one another, (iii) sorption is by the same mechanism, and (iv) adsorbed molecules do not interact. The Langmuir isotherm is expressed as Eq. 3 and linearized as given in Eq. 4.

where C is the final concentration (mg/l), q is the amount of solute (lead) adsorbed at equilibrium (mg/g), K_L(L/mg) is the Langmuir constant that represented the affinity of binding sites, and q_max(mg/g) is the maximum monolayer coverage. Figure 5 shows the Langmuir isotherm for the two sawdust species and various particle sizes with R² values ranging from 0.69 to 0.86 for Khaya ivorensis and 0.86 to 0.98 for Pycnanthus angolensis. The Langmuir isotherm performed well on the two sawdust species at their respective optimum particle sizes of 0.85 mm for Khaya ivorensis (R² = 0.97) and 1.18 mm for Pycnanthus angolensis (R² = 0.98). The lowest R² values were obtained for the smallest particle sizes of 0.3 mm for Khaya ivorensis (R² = 0.69) and 0.6 mm for Pycnanthus angolensis (R² = 0.86), which indicated that the accuracy of Langmuir isotherm in describing the sorption of lead to activated sawdust decreased when the particle size was below optimum. However, the Langmuir isotherm generally seemed to fit the experimental data for Pycnanthus angolensis better than Khaya ivorensis. The isotherm parameters q_max and K_L were obtained from the slope and intercept, respectively, of the plot of C/q against C. The maximum monolayer coverage ranged from 14.21 to 18.42 mg/g for Pycnanthus angolensis and 14.60 to 19.61 mg/g for Khaya ivorensis.  The highest maximum monolayer coverage was 19.61 mg/g for the Khaya ivorensis particle size of 0.3 mm, followed by 18.42 mg/g for the Pycnanthus angolensis particle size of 2.0 mm. The optimum particle sizes did not exhibit higher maximum monolayer coverage than other particle sizes. The maximum monolayer coverage for the optimum particle sizes was 15.49 for Khaya ivorensis and 15.43 mg/g for Pycnanthus angolensis. The values of maximum monolayer coverage obtained in this study are comparable to those of Moafi et al. (2016) and Gasemi and Gholami (2014), who obtained values of 6.67 mg/g for chromium and 10 mg/g for lead. However, these values were much lower than those obtained by Gad et al. (2013), who obtained a value of 91.6 mg/g for the adsorption of lead by pine sawdust. In order to gain further insight into the performance of the adsorbents, a comparison with other wood-based adsorbents was made in Table 5. To ascertain the range of conditions over which the adsorption of lead by activated sawdust was favorable, the dimensionless parameter R_L was estimated as follows:

where R_L is the separation factor, K_L is the constant of the Langmuir isotherm, and C₀ is initial concentration. According to Zheng et al. (2009), R_L = 0 suggests that the adsorption process is irreversible; 0 < R_L < 1 denotes a favorable process, R_L = 1 suggests that the process is linear, and R_L > 1 suggests that the adsorption process is unfavorable. Figure 6 clearly shows that the sorption of lead onto activated sawdust of Khaya ivorensis and Pycanthus angolensis was favorable for all experimental conditions and variables investigated. For all the particle sizes studied, the sorption process became more favorable at higher initial concentrations of lead. This can be attributed to the driving force generated by a high concentration gradient between the solid and liquid phase, which helps to overcome mass transfer resistance.

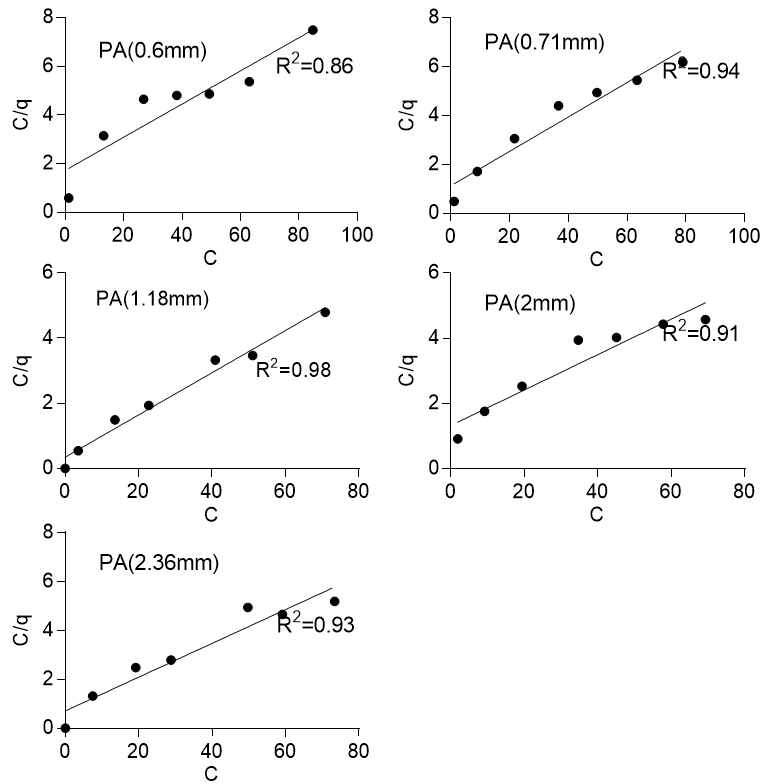
Fig. 5a. Langmuir isotherm for Pycanthus angolensis 

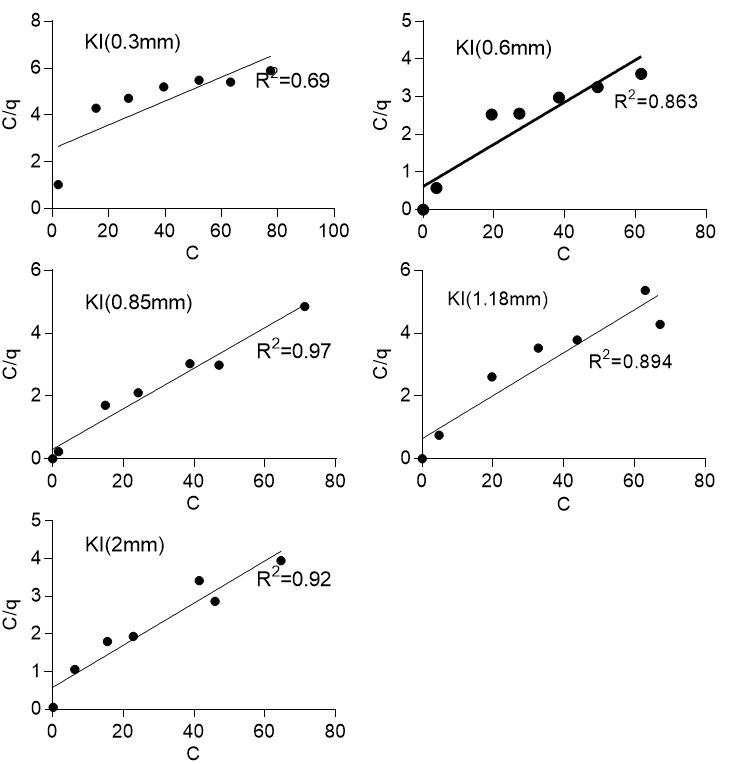
Fig. 5b. Langmuir isotherm for Khaya ivorensis

Table 5. Comparison of Lead Removal Efficiency and Sorption Capacity of Various Wood-based Adsorbents

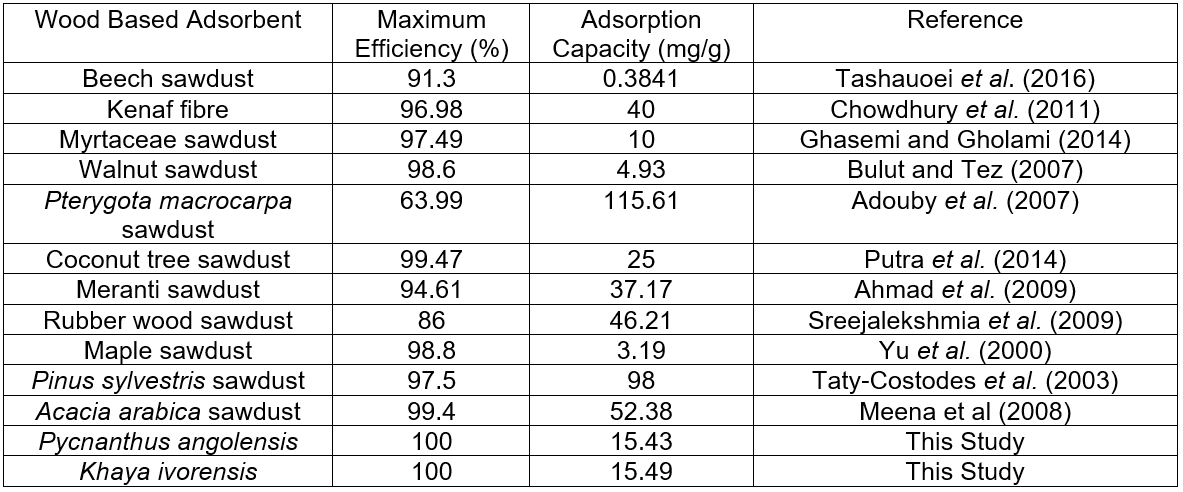
Figure 6 clearly confirms that particle size played a major role in the adsorption of lead by sawdust. However, the effect of particle size on the nature and mechanism of sorption drastically decreases as the initial concentration of lead increases. The most favorable condition occurred at an initial lead concentration of 130 mg/L at a particle size of 0.6 mm and 1.18 mm for Khaya ivorensis (R_L = 0.012) and Pycnanthus angolensis (R_L = 0.039), respectively. However, the most unfavorable sorption conditions corresponded to an initial lead concentration of 10 mg/L at a particle size of 0.3 mm and 0.6 mm for Khaya ivorensis (R_L = 0.83) and Pycnanthus angolensis (R_L = 0.71), respectively.

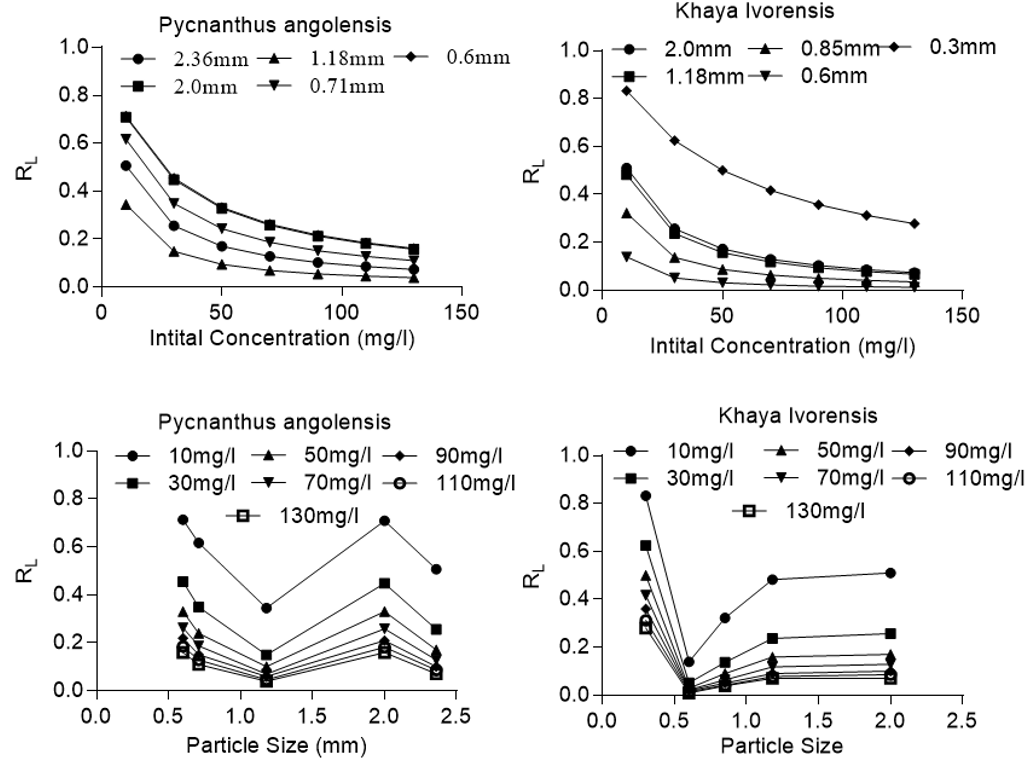
Fig. 6. Plot of equilibrium parameter (R_L) versus particle size

The experimental data were also fitted to the Freundlich isotherm. The Freundlich isotherm is suitable for describing multilayer physical sorption of solute to an adsorbent with a heterogeneous surface. The Freundlich isotherm is expressed as Eq. 6,

where q is the amount adsorbed at equilibrium (mg/g), K_f (mg/g) is the Freundlich constant, C is the concentration of the adsorbate, and n is the Freundlich number that depended on the nature of sorption, as well as the distribution of active sorption sites. Equation 6 was linearized and then applied to the experimental data, which gave an R² value ranging from 0.83 to 0.96 for Khaya ivorensis and from 0.96 to 1.0 for Pycnanthus angolensis (Fig. 7). The Freundlich isotherm gave the best fit of R² = 1.0 for Pycnanthus angolensis of particle size 0.71 mm and R² = 0.96 for Khaya ivorensis of particle size 2.0 mm. Hence, the Freundlich isotherm well described the process of adsorption onto the two types of sawdust. This was confirmed by the further examination of the values of n. The value of n gave the indication of favorability of the sorption process with values of n = 1, which indicated that the partition of solute between the two phases were independent; n > 1 indicated normal adsorption and n < 1 indicated cooperative adsorption (Mohan and Karthikeyan 1997). The sorption of lead onto the two types of sawdust was favorable with  for Pycnanthus angolensis and  for Khaya ivorensis. The n values for the optimum particle sizes were 2.67 for Khaya ivorensis and 2.54 for Pycnanthus angolensis. Desta (2013) observed that values of n > 1 were the most common and can be attributed to a distribution of surface sites or any factor that causes a decrease in adsorbent-adsorbate interaction with increasing surface density.

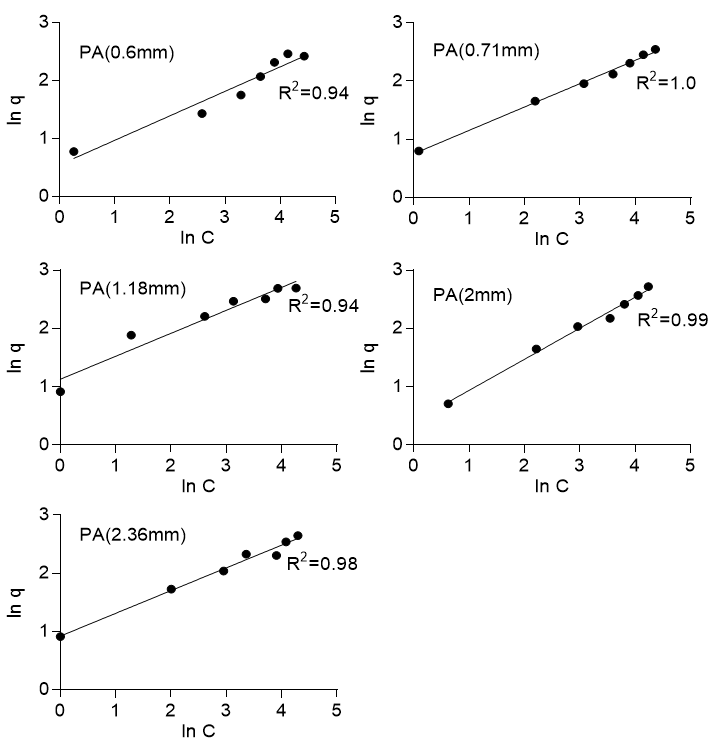
Fig. 7a. Freundlich isotherm for Pycanthus angolensis

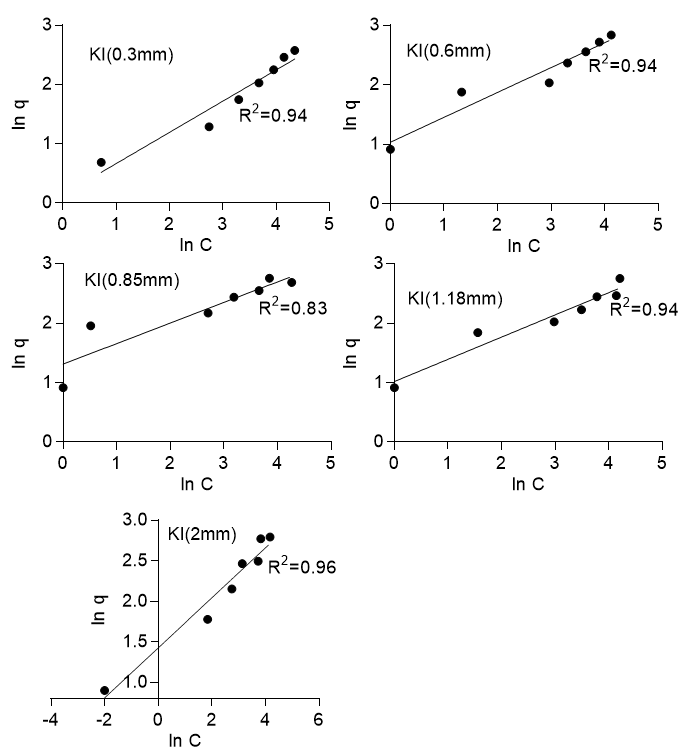
Fig. 7b. Freundlich isotherm for Khaya ivorensis 

The experimental data were also fitted to the Temkin isotherm. The Temkin isotherm considers the effect of indirect adsorbent/adsorbate interaction on the adsorption of solute to an adsorbent. The isotherm assumes that the heat of adsorption of all molecules in the layer would decrease linearly with coverage and that adsorption is characterized by an equal distribution of binding energies up to a maximum binding energy. The Temkin isotherm is expressed in Eq. 7 and linearized as shown in Eq. 8,

where B = , R is the gas constant with a value of 8.314 J/mol K, T is the temperature in Kelvin, b (J/mol) related to the heat of adsorption, and A is the isotherm constant (L/g). Figure 8 shows that the adsorption process did not necessarily conform to the Temkin isotherm, as the plot of q versus LnC was not exactly linear. The R² values ranged from 0.78 to 0.89 for Khaya ivorensis and 0.81 to 0.98 for Pycnanthus angolensis. Foo and Hameed (2010) noted that the Temkin isotherm was excellent for gas phase equilibria but was not efficient at representing liquid-solid adsorption.

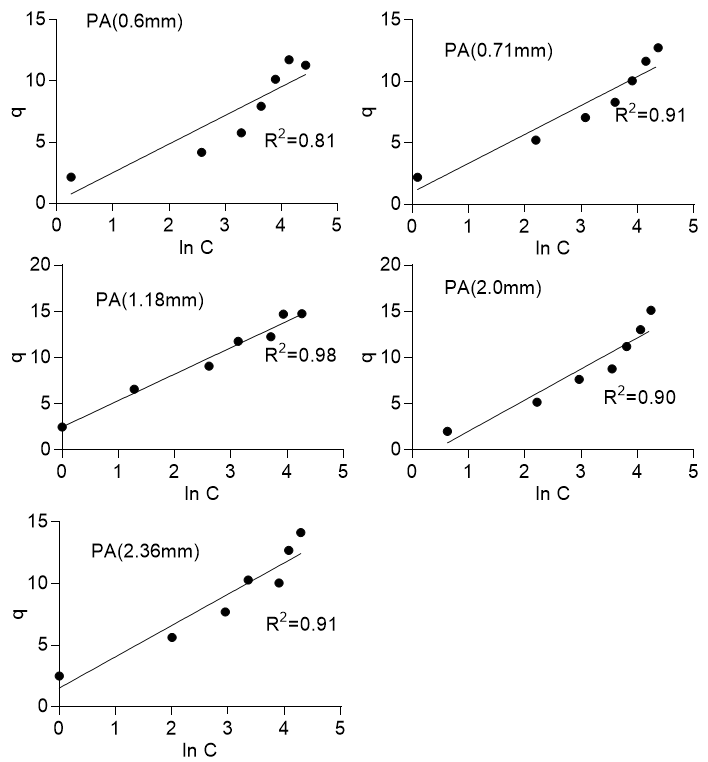
Fig. 8a. Temkin isotherm for Pycanthus angolensis

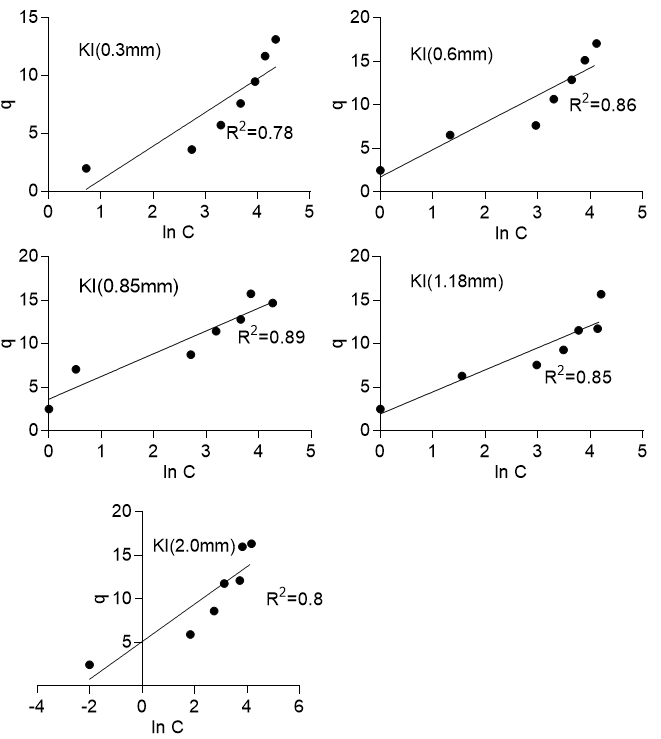
Fig. 8b. Temkin isotherm for Khaya ivorensis

Lastly, the D-R isotherm (plots not shown) was applied to the experimental data to determine the nature of the adsorption process (physical or chemical). The D-R isotherm is given as Eq. 9,

                                                                          (9)

where q (mg/g) is the amount of adsorbate adsorbed at equilibrium, q_m (mg/g) is the theoretical monolayer sorption capacity, β (mol²/J²) is the constant of the sorption energy, R is the gas constant with a value of 8.314 J/mol K, T is the temperature in Kelvin, and C is the amount of solute remaining in solution at equilibrium. The nature of adsorption can be ascertained by computing the mean sorption energy (E) with Eq. 10.

                                                                                                                   (10)

The mean sorption energy is the energy required to transfer one mole of the sorbate from infinity in solution to the surface of solid (Abasi et al. 2011). It is normally used to ascertain the nature of adsorption. The sorption mechanism is physical in nature if , which indicates low adsorption energy as a result of weak Van der Waals forces. Chemisorption processes have relatively high adsorption energies in that the adsorbate adheres to the surface through the formation of a chemical bond. Typical binding energy for the ion-exchange mechanism is in the range of 8 to 16 kJ/mol (Qureshi et al. 2009). The values of E (12.5 kJ/mol and 13.4 kJ/mol for Pycnanthus angolensis and Khaya ivorensis, respectively) obtained for the two species of sawdust indicated that lead molecules were adsorbed to the adsorbents by an ion exchange mechanism. The isotherm parameters are summarized in Table 6. Table 6 in conjunction with Fig. 9 also suggests that lead is more favourably adsorbed by Khaya ivorensis than Pycnanthus angolensis. Figure 9 shows that Khaya ivorensis has larger pores, and these facilitate the transfer of lead into the adsorbent.

Table 6. Isotherm Parameters for Optimum Sawdust Particle Sizes

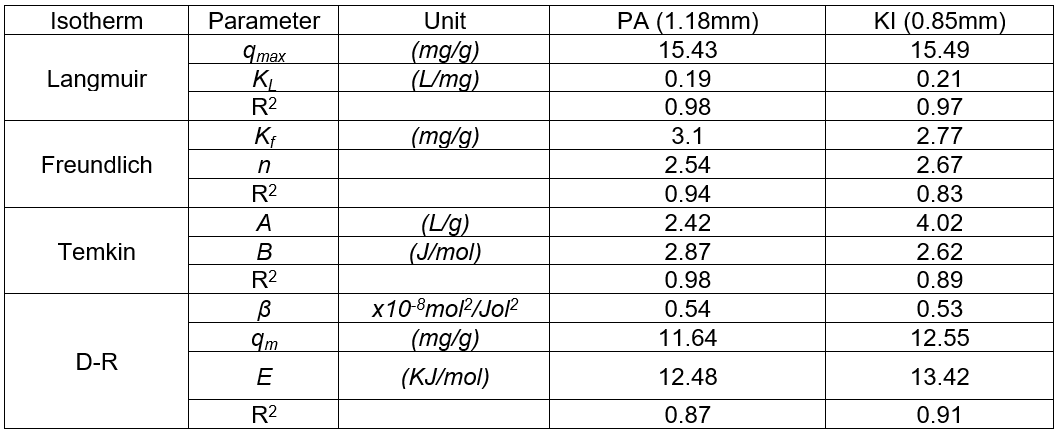
Fig. 9. SEM images of raw and activated adsorbents

The sorption kinetics provide insight into the pathways and the mechanisms of sorption reaction as well as describing the solute uptake rate, which in turn controls the residence time of solute uptake at the solute-solution interface (Ho and McKay 1999). The optimum particle sizes of the two species of sawdust were used for batch kinetic studies. The first order kinetic model (Eq. 11) was based on the assumption that the sorption of lead ions onto the activated sawdust was reversible and followed first order rate kinetics (Vinod and Anirudhan 2002),

                                                                                                    (11)

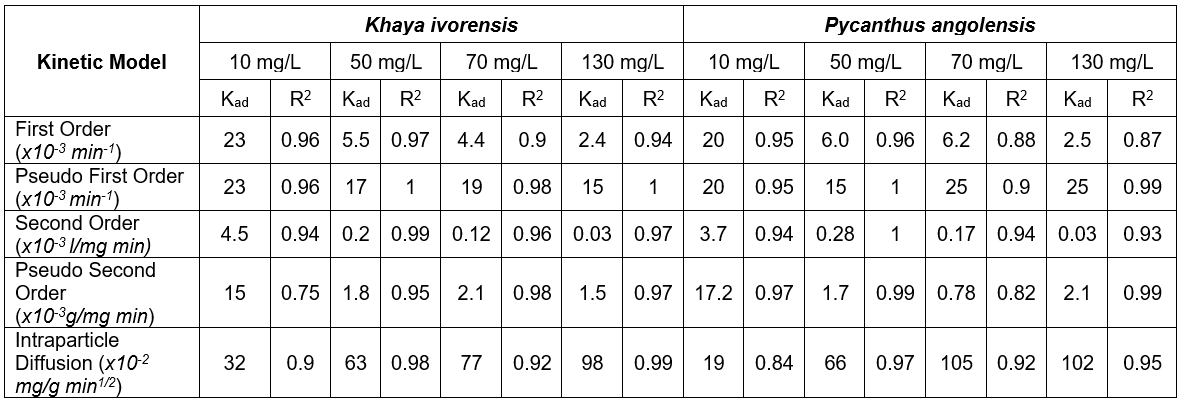
where C is the concentration at time (t), C₀ is the initial concentration, k is the rate of sorption, and t is time. The first order kinetic model described the sorption process fairly well with R² values ranging from 0.9 to 0.97 for Khaya ivorensis and 0.87 to 0.96 for Pycnanthus angolensis. The first order rate constant (k₁) was obtained from the slope of the plot of log C versus t/2.303.  The first order rate constant was reduced from 0.023 to 0.0024 min^-1 for Khaya ivorensis and 0.02 to 0.025 min^-1 as the initial lead concentration increased from 10 mg/L to 130 mg/L (Table 7). 

Table 7. Performance of Kinetic Models

The pseudo-first order kinetic equation is the most widely used rate equation for sorption of a solute from a liquid solution and may have been the first rate equation for the sorption in liquid/solid systems based on solid capacity (Ho et al. 2000). The pseudo first order kinetic model was developed by Lagergren (1898) and is given as Eq. 12 (Ho and McKay 1999),

                                                                                                  (12)

where k₁ is the rate of sorption (g/mg min), q_e the amount of lead adsorbed onto activated carbon at equilibrium (mg/g), and q the amount of lead adsorbed at any time (mg/g). The pseudo-first order rate constant was obtained from the slope of Ln (q_e – q) versus t. The R² values for the pseudo-first order kinetics ranged from 0.96 to 1.0 for Khaya ivorensis and from 0.9 to 1.0 for Pycnanthus angolensis. Accordingly, Ho and McKay (1999) reported that the majority of sorption processes reported in the literature followed the pseudo-first order kinetic mechanism. The pseudo-first order rate constant ranged from 0.023 to 0.015 min^-1 for Khaya ivorensis and from 0.02 to 0.015 min^-1 for Pycnanthus angolensis, as the concentration of lead increased from 10 mg/L to 130 mg/ L. These values are in the range of those obtained by Raji et al. (1997) for the adsorption of Pb, Hg, and Cd by activated sawdust. Figure 10 clearly shows that the pseudo-first order rate constant was less sensitive to solute concentration than other models investigated, as the pseudo-first order model was based on the sorption capacity of the adsorbent rather than the solute concentration in liquid phase.

The experimental data were also fitted to the pseudo-second order kinetic model (Eq. 13),

                                                                                                               (13)

where C is the concentration at time (t), k₂ is the sorption rate, and t is time. The second order rate constant was obtained from the slope of 1/C_t versus t. The second order kinetic model fitted the experimental data well, with ­R² ranging from 0.94 to 0.99 for Khaya ivorensis and from 0.93 to 1.0 for Pycnanthus angolensis. The second order rate constant decreased from 0.0045 to 0.000026 L/mg min for Khaya ivorensis and from 0.0037 to 0.00003 L/mg min for Pycnanthus angolensis. These values suggested that the second order model was extremely sensitive to variation in solute concentration in the liquid phase.

The pseudo second order kinetic is applicable to sorption mechanisms where the rate-limiting step involves the participation of two independently mobile functional groups at the substrate surface, or where remaining sorption sites become increasingly reluctant to fill as a result of charge repulsion, crowding, or saturation (Hubbe et al. (2012). If the rate of sorption depends on a second order equation based on the sorbate uptake, the pseudo-second order chemisorption kinetics may be expressed as Eq. 14 (Ho et al. 2000),

                                                                                                            (14)

where k_2s is the rate of sorption (g/mg min), q_e is the amount of lead adsorbed onto activated sawdust at equilibrium (mg/g), and q is the amount of lead adsorbed at any time (mg/g). A plot of t/q_t against t reveals a linear relationship whose intercept can be used to obtain the pseudo-second order rate constant. The pseudo-second order rate constant was generally lower than those of the first order and pseudo-first order models with R² values ranging from 0.75 to 0.98 for Khaya ivorensis and 0.82 to 0.99 for Pycnanthus angolensis.

The intraparticle diffusion model is applicable in cases where intraparticle diffusion was the rate-limiting step (Attia et al. 2010). If the rate-limiting step is intraparticle diffusion, a plot of solute adsorbed against square root of contact time should yield a straight line passing through the origin (Weber and Morris 1963). The intraparticle diffusion model was given as Eq. 15,

                                                                                                             (15)

where q_t (mg/g) is the amount adsorbed at time t (min), k_d (mg/g/min-0.5) is the intra-particle rate constant, and I_d is the rate of adsorption at time zero. Plots of q_t versus t were linear and nearly passed through the origin with values of I_d ranging from -0.1303 to 0.8625 for Khaya ivorensis and -0.943 to 2.303 for Pycnanthus angolensis. The intraparticle diffusion rate ranged from 0.32 to 0.98 mg/g min^1/2 for Khaya ivorensis and 0.19 to 1.017 mg/g min^1/2 for Pycnanthus angolensis. Zheng et al. (2009) obtained very similar values (0.14 to 0.98 mg/g min^1/2) for the sorption of aniline to bentonite at initial solute concentrations ranging between 20 and 120 mg/L.

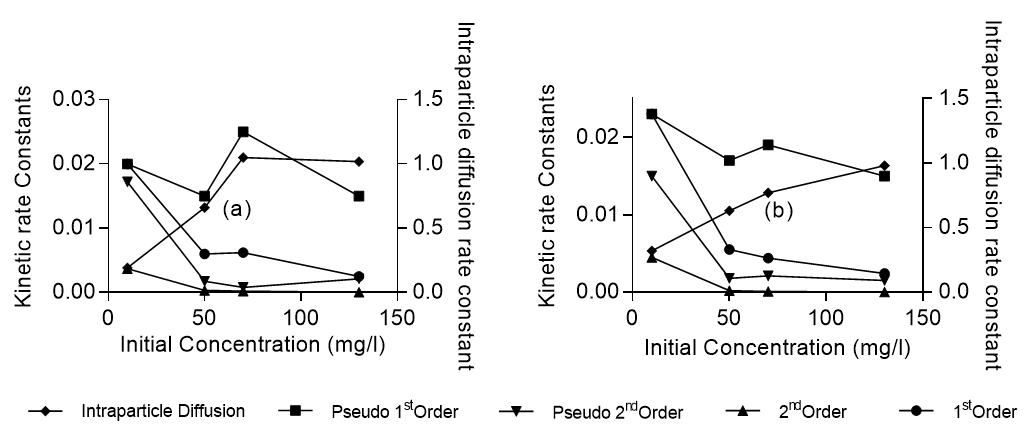
Fig. 10. Variation of rate of sorption rate constants with initial lead concentration

Judging by the R² values, the pseudo first order kinetic model accurately mimicked the adsorption kinetics in all cases with 0.96 ≤ R²≤ 1.0 for Khaya ivorensis and 0.9 ≤ R²≤ 1.0 for Pycnanthus angolensis. The first order kinetic model performed very well at low initial lead concentrations of 10 mg/L for Khaya ivorensis and Pycnanthus angolensis with R² values of 0.96 and 0.95, respectively. In contrast, the intraparticle kinetic model performed well at medium and high concentrations of lead ranging from 50 to 130 mg/L. However, on the basis of absolute mean error (AME), the intraparticle diffusion model outperformed all other models, having the lowest AME of 7.39 and 4.64 for Pycnanthus angolensis and Khaya ivorensis, respectively. It was closely followed by the pseudo first order model with an AME of 11.72 and 11.35 for Pycnanthus angolensis and Khaya ivorensis, respectively. Table 7 shows that the intraparticle diffusion rate constant increased with initial lead concentration. This suggests that intraparticle diffusion is favored at high concentrations of lead. Increasing the lead concentration from 10 mg/L to 130 mg/L resulted in a threefold increase of the intraparticle diffusion rate constant for Khaya ivorensis and a fivefold increase for Pycnanthus angolensis. The pseudo first order model yielded higher rate constants than those of the first order, second order, and pseudo second order kinetic models (Fig. 10). However, the rate constants of the other models decreased as initial concentrations decreased. 

CONCLUSIONS

1. This study showed that sawdust, which is usually discarded as a waste material, could be effectively utilized in water and wastewater treatment.
2. Using a combination of the right particle sizes and initial lead concentration can optimize the sorption process.
3. Though low initial lead concentration yields higher adsorption efficiency, higher initial lead concentration leads to the adsorption of more quantities of solute due to the higher concentration potential.
4. Lead is adsorbed to the sawdust of the two species by ion exchange.
5. The pseudo-first order and the intraparticle diffusion models can be used for the design of sorption reactors.

REFERENCES CITED 

Abasi, C. Y., Abia, A. A. and Igwe, J. C. (2011). “Adsorption of iron (III), lead (II), and cadmium (II) ions by unmodified raphia palm (Raphia hookeri) fruit endocarp,” Environmental Research Journal 5(3), 104-103. DOI: 10.3923/erj.2011.104.113

Adouby, K., Akissi, L. C., Wandan, N., and Yao, B. (2007). “Removal of heavy metal ions (Pb⁺, Cu²⁺) in aqueous solutions by Pterygota macrocarpa sawdust,” Journal of Applied Sciences 7(14), 1864-1872.

Ahmad, A., Rafatullah, M., Sulaiman, O., Ibrahim, H. M., Chii, Y. Y. and Siddique, B. M. (2009). “Removal of Cu (II) and Pb (II) ions from aqueous solutions by adsorption on sawdust of meranti wood,” Desalination 250, 300-310.

Argun, M., Dursun, S., Ozdemir, C. and Karatas, M. (2007). “Heavy metal adsorption by modified oak sawdust: Thermodynamics and kinetics,” Journal of Hazardous Materials 141, 77-85. DOI: 10.1016/j.jhazmat.2006.06.095

Attia, A., Khedr, S. and Elkholy, S. (2010). “Adsorption of chromium ion (VI) by acid activated carbon,” Brazilian Journal of Chemical Engineering 27 (1), 183-193. DOI: 10.1590/S0104-66322010000100016

Bailey, S. E., Olin, T. J., Bricka, R. M., and Adrian, D. D. (1999). “A review of potentially low-cost sorbents for heavy metals,” Water Research 33(11), 2469-2479. DOI: 10.1016/S0043-1354 (98)00475-8

Begum, K., and Alhaji, N. (2013). “Adsorption efficiency of sawdust in activated and surface-modified forms – A comparative study,” Chemical Science Transactions 2(4), 1364-1369. DOI:10.7598/cst2013.689

Byrant, P. S., Petersen, J. N., Lee, J. M., and Brouns, T. M. (1992). “Sorption of heavy metals by untreated red fir sawdust,” Applied Biochemistry and Biotechnology 34-35, 777-788. DOI: 10.1007/BF02920596

Bulut, Y., and Tez, Z. (2007). “Removal of heavy metals from aqueous solution by sawdust adsorption,” Journal of Environmental Sciences 19, 160-166. DOI: http://dx.doi.org/10.1016/S1001-0742(07)60026-6

Chowdhury, Z., Zain, S., Khan, R., and Ashraf, M. (2011). “Preparation, characterization and adsorption performance of the KOH-activated carbons derived from kenaf fiber for lead (II) removal from waste water,” Scientific Research and Essays 6(29), 6185-6196. DOI: 10.5897/SRE11.1436.

Desta, M. B. (2013). “Batch sorption experiment: Langmuir and Freundlich isotherm studies for the adsorption of textile metal ions into teff straw (Eragostis tef) agricultural waste,” Journal of Thermodynamics 375830. DOI: 10.1155/2013/37580

Fayemiwo, K., Awojide, O., and Ganiyu, T. (2013). “Comparative analysis of two low cost metal adsorbents (rice husk and sawdust),” International Journal of Environmental Sciences 5(6), 1245-1248.

Foo, K. Y., and Hameed, B. H. (2010). “Insight into modelling of adsorption systems,” Chemical Engineering Journal 156, 2-10. DOI: 10.1016/j.cej.2009.09.013

Gad, H., Omar, H., and Khadil, M. (2013). “Factors affecting sorption of Pb(II) from aqueous solution using sawdust based activated carbon,” Journal of American Sciences 9(10), 95-106.

Ghasemi, S., and Gholami, R. M. (2014). “Kinetic and isotherm study of lead adsorption from synthetic wastewater by Myrtaceae sawdust,” Bulletin of Environment, Pharmacology, and Life Sciences Bull. Env. Pharmacol. Life Sci., 3(11) 157-165.

Ho, Y. S., and McKay, G. (1999). “Pseudo-second order model for sorption processes,” Process Biochemistry 34, 451-465. DOI: 10.1016/S0032-9592(98)00112-5

Ho, Y. S., Ng, J. C. Y., and McKay, G. (2000). “Kinetics of pollutant sorption by biosorbents: A review,” Separation and Purification Methods 29(2), 189-232. DOI:  10.1081/SPM-100100009

Hubbe, M. A., Hasan, S. H., and Ducoste, J. J. (2011). “Cellulosic substrates for removal of pollutants from aqueous systems: A review. 1. Metals,” BioResources 6(2),       2161-2287.

Hubbe, M. A., Beck, K. R., O’Neal, W. G., and Sharma, Y. C. (2012). “Cellulosic substrates for removal of pollutants from aqueous systems: A review. 2. Dyes,” BioResources 7(2), 2592-2687.

Kalavathy, H. M., Regupathi, I., Pillai, M. G., and Miranda, L. R. (2009). “Modelling, analysis, and optimization of adsorption parameters for H₃PO₄ activated rubber wood sawdust using response surface methodology (RSM),” Colloids and Surfaces B: Biointerfaces 70, 35-45. DOI: 10.1016/j.colsurfb.2008.12.007

Lagergren, S. (1898), “About the theory of so-called adsorption of soluble substances,”    K. Sven. Vetenskapsakad. Handl. 24 (4), 1-39.

Maharani, R., Yutaka, T., Yajima, T., and Minoru, T. (2010). “Scrutiny on physical properties of sawdust from tropical commercial wood species: Effects of different mills and sawdust’s particle size,” Journal of Forestry Research 7(1), 20-32. DOI: 10.20886/ijfr.2010.7.1.20-32

Mane, V. S., and Vijay-Babu, P. V. (2011). “Studies on the adsorption of Brilliant Green dye from aqueous solution onto low-cost NaOH treated sawdust,” Desalination 273, 321-329. DOI: 10.1016/j.desal.2011.01.049

Meena, A., Kadirvelu, K., Mishra, G., Rajagopal, C., and Nagar, P, N. (2008). “Adsorptive removal of heavy metals from aqueous solution by treated sawdust (Acacia arabica),” Journal of Hazardous Materials 150(3), 604-611.

Moafi, H. F., Ansari, R., and Ostovar, F. (2016). “Ag₂O/Sawdust nanocomposite as an efficient adsorbent for removal of hexavalent chromium ions from aqueous solutions,” Journal of Materials and Environmental Science. 7(6), 2051-2068.

Mohan, S., and Karthikeyan, J. (1997), “Removal of lignin and tannin colour from aqueous solution by adsorption on to activated charcoal,” Environmental Pollution. 97, 183 – 187.

Naiya, T., Chowdhury, P., Bhattacharya, A., and Das, S. (2009). “Sawdust and neem bark as low-cost natural biosorbent for adsorptive removal of Zn(II) and Cd(II) ions from aqueous solutions,” Chemical Engineering Journal 148, 68-79. DOI: 10.1016/j.cej.2008.08.002

Pal, J., and Kaur, M. (2013). “Adsorption of hexavalent chromium from textile industry effluent by sawdust of Dalbergia sissoo,” Journal of Environmental Science and Sustainability 1(1), 34-40.

Putra, W.P., Kamari, A., Yusoffi, S. N., Ishak, C. F., Mohamed, A., Hashim, N., and Isa, I. M. (2014). “Biosorption of Cu(II), Pb(II) and Zn(II) ions from aqueous solutions using selected waste materials: Adsorption and characterization studies,” Journal of Encapsulation and Adsorption Sciences 4, 25-35. DOI: 10.4236/jeas.2014.41004

Qureshi, I., Memon, S., and Yilmaz, M. (2009). “Estimation of chromium (VI) sorption efficiency of novel regenerable p-tert-butylcalix [8] areneoctamide impregnated Amberlite resin,” Journal of Hazardous Materials 164, 675-682. DOI: 10.1016/j.jhazmat.2008.08.076

Raji, C., Manju, G., and Anirudhan, T. (1997). “Removal of heavy metal ions from water using sawdust based -activated carbon,” Indian Journal of Engineering and Materials Sciences 4, 254-260.

Sreejalekshmia, K., Anoop Krishnanb, K., and Anirudhana, T. (2009). “Adsorption of Pb(II) and Pb(II)-citric acid on sawdust activated carbon: Kinetic and equilibrium isotherm studies,” Journal of Hazardous Materials 161, 1506-1513.

Tashauoei, H., Hashemi, S., Ardani, R., Yavari, Z. and Asadi–Ghalhari, M. (2016). “Adsorption of lead from aqueous solution by modified beech sawdust,” Journal of Safety, Environment and Health Research 1(1), 11-16, DOI: 10.22053/jsehr.2016.33382.

Taty-Costodes, V., Fauduet, H., Porte, C., and Delacroix, A. (2003). “Removal of Cd (II) and Pb (II) ions, from aqueous solutions, by adsorption onto sawdust of Pinus sylvestris,” Journal of Hazardous Materials 105(1-3), 121-142.

Vinod, V. and Anirudhan, T.  (2002). “Sorption of tannic acid on zirconium pillared clay,” Journal of Chemical Technology and Biotechnology 77(1), 92-101. DOI: 10.1002/jctb.530

Weber, J., and Morris, J. (1963). “Kinetics of adsorption on carbon from solution,” Journal of Sanitary Engineering Division 89(2), 31-60.

Yu, B., Zhang, Y., Shukla, A., Shukla, S. and Dorris, K. (2000). “The removal of heavy metals from aqueous solutions by sawdust adsorption – Removal of lead and comparison of its adsorption with copper,” Journal of Hazardous Materials 80(1-3), 33-42.

Zheng, H., Liu, D., Zheng, Y., Liang, S., and Liu, Z. (2009). “Sorption isotherm and kinetic modeling of aniline on Cr-bentonite,” Journal of Hazardous Materials 167, 141-147. DOI: 10.1016/j.jhazmat.2008.12.093

Article submitted: November 8, 2016; Peer review completed: February 25, 2017; Revised version received and accepted: April 17, 2017; Published:  April 24, 2017.

DOI: 10.15376/biores.12.2.4123-4145