Abstract
Knowledge of the force required to overcome deformation at the proportionality limit, maximum limit, and their ratio, as well as knowledge of the effect of selected factors on the listed characteristics in bending stress, have both scientific and practical significance. They form a foundation for designing tools for bending and determine the stress that products and their parts can be exposed to during use. This study analyzes the effect of selected factors on the force at the proportionality limit (FE), the force at the maximum limit (FP), and the ratio of these two characteristics (FE/FP). This study examined the effect of the wood species (WS) (Fagus sylvatica L. and Populus tremula L.), material thickness (MT) (4 mm, 6 mm, 10 mm, and 18 mm), degree of densification (DOD) (0%, 10%, and 20%), and the number of cycles (NOC) (0 or 10,000), as well as their combined interaction, on the monitored characteristics. The results contribute to the advancement of knowledge necessary for the study and development of new materials with specific properties for their intended use. The results can improve the innovative potential of wood processing companies and increase their performance and competitiveness in the market.
Download PDF
Full Article
Bending Forces at the Proportionality Limit and the Maximum – Technological Innovations for Better Performance in Wood Processing Companies
Tomáš Svoboda,a Zuzana Gaffová,b,* Rastislav Rajnoha,c Anna Šatanová,d and Richard Kminiak a,*
Knowledge of the force required to overcome deformation at the proportionality limit, maximum limit, and their ratio, as well as knowledge of the effect of selected factors on the listed characteristics in bending stress, have both scientific and practical significance. They form a foundation for designing tools for bending and determine the stress that products and their parts can be exposed to during use. This study analyzes the effect of selected factors on the force at the proportionality limit (FE), the force at the maximum limit (FP), and the ratio of these two characteristics (FE/FP). This study examined the effect of the wood species (WS) (Fagus sylvatica L. and Populus tremula L.), material thickness (MT) (4 mm, 6 mm, 10 mm, and 18 mm), degree of densification (DOD) (0%, 10%, and 20%), and the number of cycles (NOC) (0 or 10,000), as well as their combined interaction, on the monitored characteristics. The results contribute to the advancement of knowledge necessary for the study and development of new materials with specific properties for their intended use. The results can improve the innovative potential of wood processing companies and increase their performance and competitiveness in the market.
Keywords: Technological and product innovations; Cyclic loading; Laminated wood; Force at the proportionality limit; Force at the maximum limit; Force ratio; Wood-processing industry performance
Contact information: a: Department of Wood Processing, Czech University of Life Sciences in Prague, Kamýcká 1176, Prague 6 – Suchdol, 16521 Czech Republic; b: Department of Forest and Wood Products Economics, Czech University of Life Sciences in Prague, Kamýcká 1176, Praha 6 – Suchdol, 16521 Czech Republic; c: Faculty of Economics and Business, Рan-European University, Tomášikova 20, Bratislava, 821 02 Slovak Republic; d: College of International Business ISM Slovakia in Prešov, Prešov, Slovakia;
* Corresponding author: risko.kminiak@gmail.com
INTRODUCTION
If a company is interested in sustaining their business for as long as possible, it is necessary to realize that innovations drive business and are regarded as an essential tool to maintain competitiveness. Innovations in relation to the increase of technological process efficiency guarantee the strategic growth of the company and orient management decisions towards knowledge that is represented by innovative technologies or products. Today, companies face high demands that force them to think about how to best optimize technological processes. Improvement and optimization of production and technological processes impinge on the end boards, therefore, it is necessary to find the potential for increasing the efficiency of production processes (Chromjaková and Rajnoha 2009). The recent research results show the overall conclusion that companies in the Slovak Republic wood processing industry that have outstanding performance are strongly focused on technological innovations (Rajnoha and Lorincová 2015). The authors focused on whether the firms permanently engaged in an innovation process, because it is not an event or separate action, and therefore must be controlled systematical. Enterprises cannot afford to upgrade on a random basis. The research conducted by Chromjaková and Rajnoha (2009) and Rajnoha and Lorincová (2015) showed that companies reaching higher performance give focus to strategic indicators as technological innovations.
This article aims to expand the knowledge about the effect of selected factors (wood species, material thickness, and the number of cycles) on the value of forces that lead to deformation (bending) in parts under bending moment stress. When a resultant of internal forces is in the section perpendicular to the longitudinal axis, the authors call this the bending moment and name it Mo.
Fig. 1. Force affecting the beam under bending stress (M0 – bending moment, C- center)
In terms of loading an object with a certain force, F, the deformation may be a desirable (bending) or undesirable (furniture, structural components in frames) effect of loading. It is clear that the amount of force, duration of its effect, type of loaded material, climatic conditions, and other factors affect the amount of strain- deformation of the material’s properties. The words deformation of the material describe a change in the shape and size, and depending on the amount of the applied force and the properties of the material, the change could be temporary (flexible deformation or elastic deformation over time), or permanent (plastic deformation) depending on the internal resistance of the material.
All materials deform via the effect of forces, whether they are a result of applied external stress, internal thermal, or internal moisture stress (Bodig and Jayne 1982; Wiemann 2010; Gaff et al. 2015a, 2016, 2017).
The force at the proportionality limit of wood is characterized by the limit at which the wood begins to develop elastic deformation over time and plastic deformation (Mackes and Lynch 2001). Up to this point, when the wood is loaded by stress that only causes elastic deformation, it is only elastically stressed. This is the force that can be applied to the wood with no apparent permanent deformation of its size or shape. In practical terms, it is the critical force beyond which permanent (desirable or undesirable) changes begin to form in the product parts.
Each change in the beam subjected to bending is a result of the work that is directly dependent on the applied force and the resulting deformation (Wagenfuhrer et al. 2006; Gaff et al. 2015b). In deformation within the maximum limit, the range of external forces performing the work changes. The internal forces caused by the deformation are also moved (Kamke 2006). The potential energy accumulates in an elastically deformed object, which is converted into work that is consumed to return the object to its original state when the object is unloaded (Sandberg and Navi 2007; Gaff et al. 2015c; Igaz et al. 2015; Igaz et al. 2016).
A force beyond the proportionality limit causes the development of elastic deformation over time and plastic deformation. Their development in relation to the stress is not linear. The force beyond the proportionality limit to the maximum limit characterizes the work that is required to mold the object to its breaking point.
The amount of force applied within the elastic and viscoplastic limit reflects the structure of the material, binding energy, water content, temperature, stress state, load speed, thickness of beams, and other factors.
It could be said that the force applied in the viscoplastic area is a measure of the wood’s deformation resistance (Schellberg 2012). If low toughness and good plasticity in wood are able to be achieved, it is easier to deform, bend, and mold it, therefore requiring less energy for the process.
Based on the knowledge of deformation and the behavior of materials under stress, the materials can be divided into the following different groups: flexible material, plastic material, flexible-plastic, fragile, malleable, and tough.
If one wants to describe the mechanical properties of materials, and consider their further use in products based on the acquired knowledge, a stress-strain or force-deformation diagram is required. These diagrams are essentially a material’s “identity card,” that allows a number of important characteristics to be identified. The curves in a stress-strain or force-deformation diagram may vary (Fig. 2). These graphs characterize the course of the stressed material’s resistance to deformation and failure.
The forces and their ratio are also important in describing the material’s properties and in the consideration of their future use.

Fig. 2. Examples of a force-deformation diagram; Figures 2a-e represent fictitious models of stress-strain diagrams; A- fictitious, ideally tough material; B- fictitious, ideally plastic material;
C- linear elastic material; D- linear elastic and ideally plastic behavior without strain hardening; E- material with linear elastic range and linear plastic strain hardening; and F- real diagram
Based on this information, one can use the ratio of the forces required to reach the proportionality limit and the maximum limit to make assumptions about the properties of the materials in their assessment in further processes of the creation of laminated materials (with specific properties for their intended use).
The ratio of forces during bending depends on all of the properties of the material. During bending, the wood is forced to deform in a preselected direction, i.e. the character of the deformation will be forced (Wagenführ 2000; Blomberg et al. 2005; Gaff et al. 2015a, 2016, 2017; Ružiak et al. 2017).
Wood is characterized by the fact that its toughness and plasticity are very much lower than its saturation point (Rajnoha and Lorincová 2015). This means that with a moisture content at the saturation point one expends several times less energy, thus, less force is required for deformation, but one still does not achieve the required malleability. Increased malleability can be achieved by the interaction of water and high temperatures. Either way, different wood species can behave differently. The significance of evaluating material properties based on the ratio of forces is shown in Fig. 3. A synergistic effect of increased moisture and temperature results in a decrease in the forces at the proportionality limit and at the maximum limit, as well as the relative changes between the two forces (Požgaj et al. 1997; Gašparík and Gaff 2015a,b). The wood is less resistant to the effect of the forces, and it becomes more malleable. Its deformation in the plastic range requires a much lower force to achieve greater deformation (Fig. 3c, d, e, f) (Fortino et al. 2013).
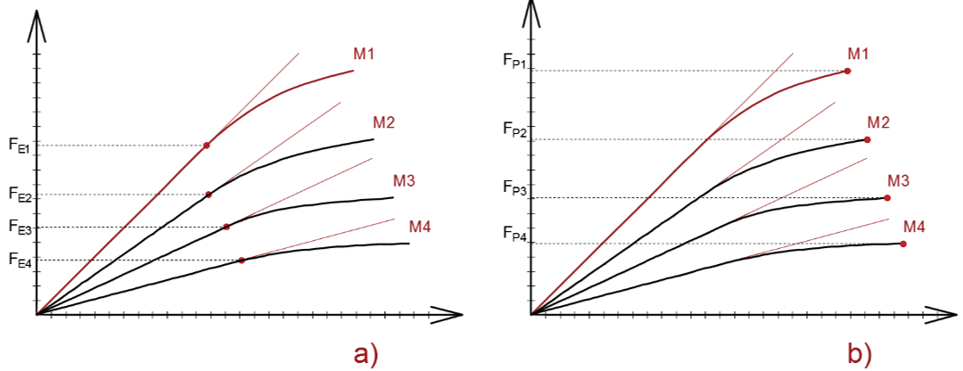
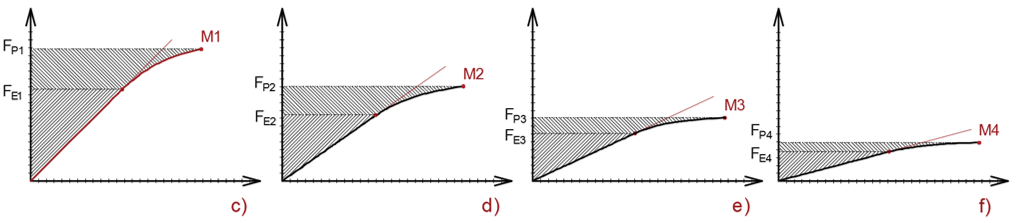
Fig. 3. Force-deformation diagram and the effect of moisture content on a) the amount of force at the maximum limit b) the amount of force at the proportionality limit
Based on the ratio of forces, the materials can be divided into different groups characterizing their suitability for a specific purpose of use.
Material with a high percentage in the plastic limit means that the plastic deformation of the material absorbs a large part of the force for its shaping; thus the applied mechanical energy is expended for plastic deformation of the material. A material with a high ability to resist stress within plastic deformation is unsuitable for bending from a non-energy perspective.
The opposite of toughness is fragility. If fragile materials do not deform plastically, then they are also non-plastic. However, tough materials have good strength and plasticity. Therefore, fragility is not the complete opposite of toughness.
Flexibility (elasticity) is a material’s ability to deform elastically before it breaks. In physics terms, elasticity is a change in material that occurs under the effect of mechanical forces, and which manifests itself by the deformation of its volume.
Plasticity is a material’s ability to change its shape in its solid state under external forces permanently without breaking, i.e. to plastically deform before breaking. The degree of plasticity under mechanical stress is plastic deformation. The physical nature of plasticity varies in different materials (wood, metal, macromolecular thermoplastics, etc.).
A frequent cause of the failure of furniture parts is stress by repetitive strain, which adversely affects the overall durability of the finished products (Bezazi and Scarpa 2007; Sandberg et al. 2013). The obtained data provides knowledge that can be used to decide whether the application of a tested material is suitable for its intended purpose of use. These innovations in relation to increasing process efficiency guarantee decisions towards gaining knowledge via innovative wood products.
EXPERIMENTAL
Materials
The experiments were conducted on lamellas with a thickness of 4 mm, 6 mm, 10 mm, and 18 mm, a width of 35 mm, and length of 600 mm. The lamellas were made from beech wood (Fagus sylvatica L.), and the results were compared with results measured in aspen wood (Populus tremula L.) from the Polana region in Slovakia. The effect of the degree of densification on the monitored characteristics was assessed by comparing the measured values (on non-densified specimens) with the values obtained from specimens that were 10% densified and specimens that were 20% densified of their original thickness perpendicular to the grain. The effect of cyclic loading was evaluated by comparing the results that were obtained from specimens before cyclic loading (number of cycles = 0) and after cyclic loading (number of cycles = 10,000). The samples were conditioned to the moisture content of 8% in a climate chamber Binder (ED, APT Line II; Tuttlingen, Germany) at a relative humidity of 40% and temperature of 20 °C.
Methods
Densification of test specimens
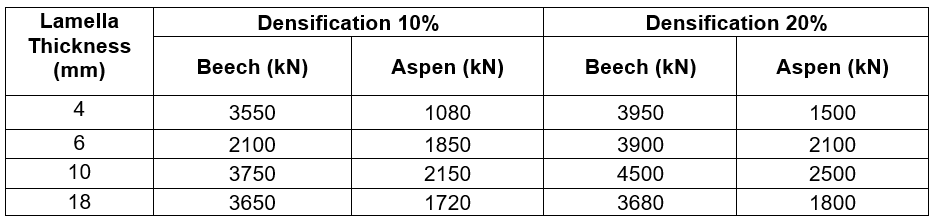
Test specimens that were intended for densification were pressed in a hydraulic press (RK Prüfsysteme MFL 1000, Leipzig, Germany). The densification process of each set of test specimens is shown in Table 1.
Table 1. Compressive Load on Each Set of Test Specimens
Determination of bending strength and modulus of elasticity
After the cyclic loading, the support span was adjusted to L1 = 20 × h (support span was changed in relation to thickness of material combinations). The samples were bent in middle-length distance using a universal testing machine FPZ 100 (TIRA, Schalkau, Germany) in accordance with EN 310 (1993), Eilmann et al. (2014), and ISO 13061-2 (2014). The loading speed was set to 3 mm/min so that the test duration would not exceed 2 min. The maximum breaking forces of samples were measured using the datalogger ALMEMO 2690-8 (Ahlborn GmbH, Braunschweig, Germany).
Evaluation and Calculation
To determine the influence of the individual factors on the bending characteristics, an analysis of variance (ANOVA) and the Fischer F-test were performed using Statistica 12 (Statsoft Inc., Tulsa, USA) software.
The wood density was determined before and after testing according to ISO 13061-1 (2014) and Eq. 1,

where ρw is the density of the sample at moisture content w (kg/m3); mw is the mass (weight) of the sample at moisture content w (kg); aw, bw, and lw are dimensions of the sample at moisture content w (m); and Vw is the volume of the sample at moisture content w (m3).
The moisture content of samples was determined and verified before and after testing. These calculations were performed according to ISO 13061-1 (2014) and Eq. 2,

where w is the moisture content of the samples (%), mw is the mass (weight) of the samples at moisture content w (kg), and m0 is the mass (weight) of the oven-dry samples (kg). Drying to an oven-dry state was also performed according to EN 310 (1993).
For the conversion between Pw and P12, the equation specified in ISO 13061-2 (2014) was employed; this is valid for a moisture content in the range between 7% and 17% (Eq. 3),

where K is the coefficient of volumetric shrinkage at a humidity change of 1%. For approximate calculations, K = 0.85 · 10-3. ρw was used, where the density is expressed in (kg/m3).
The force at the proportionality limit (FE) by static bending was determined from a force-deformation diagram specifying a 1% deviation from the linear equation (red dot in Fig. 1). The force at the maximum limit (FP) was determined as the force at which the test specimen failed.
The percentage force ratio was calculated according to Eq. 4,

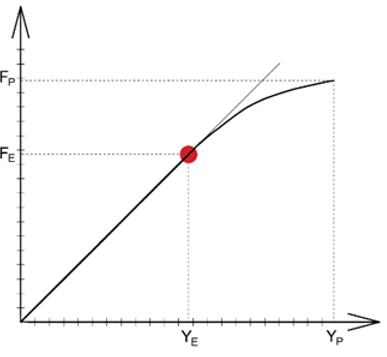
Fig. 4. Force-deformation diagram during bend loading
Cyclic bend loading
The cyclic loading was performed on a cycler machine with cyclic bending of the test pieces using single-axis loading. The following numbers of cycles were selected for testing: 0 and 10,000. During the preliminary experimental testing, the test pieces were loaded with static bending to determine the breaking strength and proportionality limit because the test pieces had to be loaded up to 90% of the proportionality limit.
RESULTS AND DISCUSSION
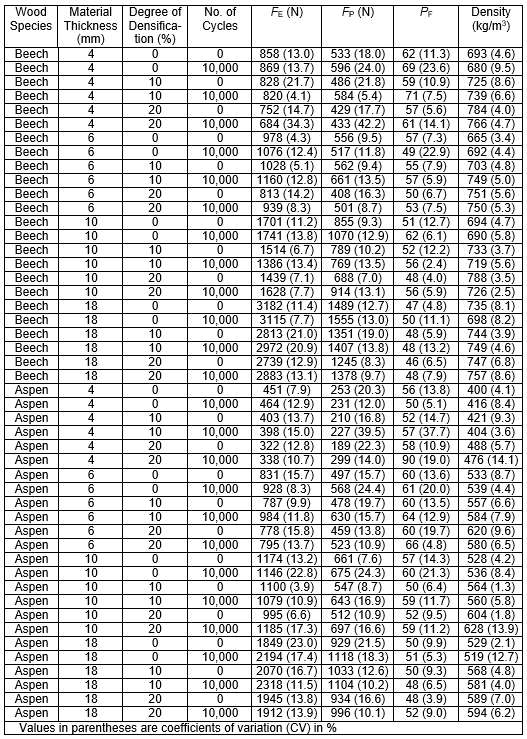
Table 2 shows the average values of the monitored characteristics, the average density values measured in individual sets of test specimens, and the corresponding coefficient of variation.
Table 2. Average Values of Bending Characteristics, Density, and Coefficient of Variance
Force at the Proportionality Limit and Force at the Maximum limit
Based on the significance level, P, shown in Tables 3 and 4, it can be concluded that all of the monitored factors could be considered to have a significant effect on both the force at the proportionality limit (Table 3) and the force at the maximum limit (Table 4). The synergistic effect of the interaction of all monitored factors was shown to have a significant effect on both monitored characteristics (Tables 3 and 5). Also, multi-factor interactions can be considered to be significant, such as WS * MT, WS * DOD, DOD * MT, in assessing the proportionality limit. In the event of force characteristics at the maximum limit, a significant effect was manifested only by the interacting factors WS * MT. Other interactions could not be considered significant. The respective model explained roughly 92% of the total sum of squares (variance of the data) at the proportionality limit.
Table 3. Statistical Evaluation of the Effect of Factors and their Interaction on the Force at the Proportionality Limit
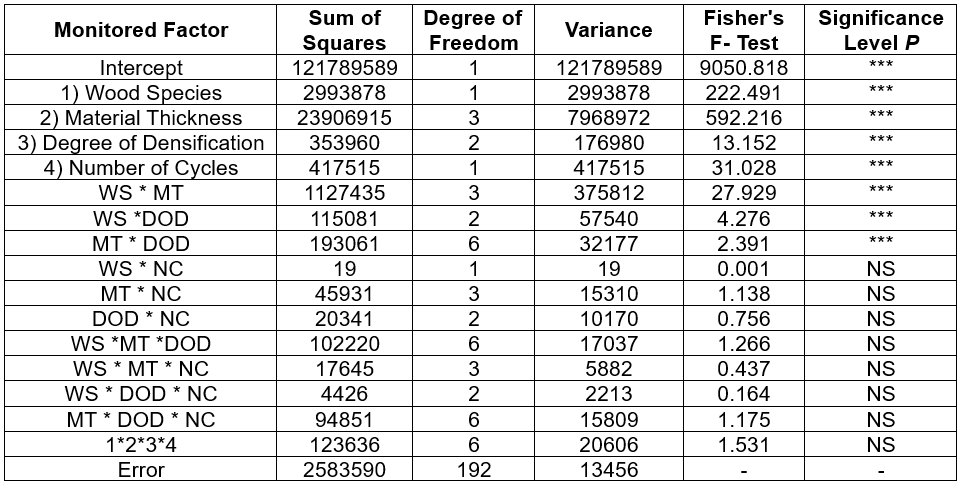
NS- not significant, ***- significant at p<0.005
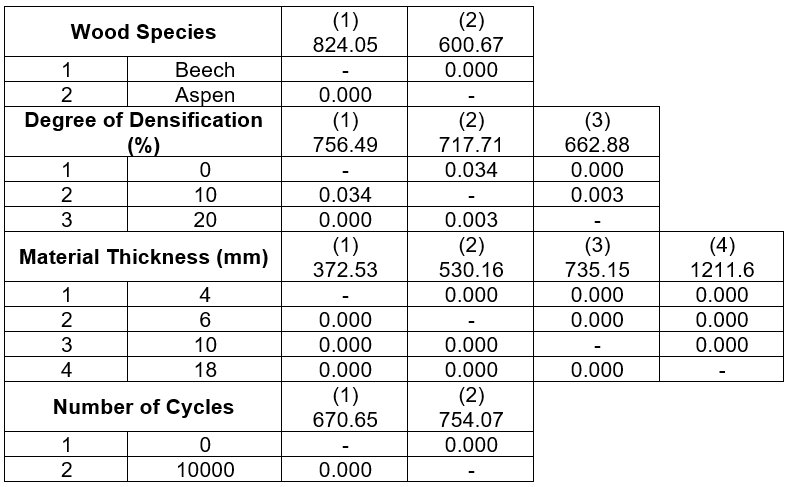
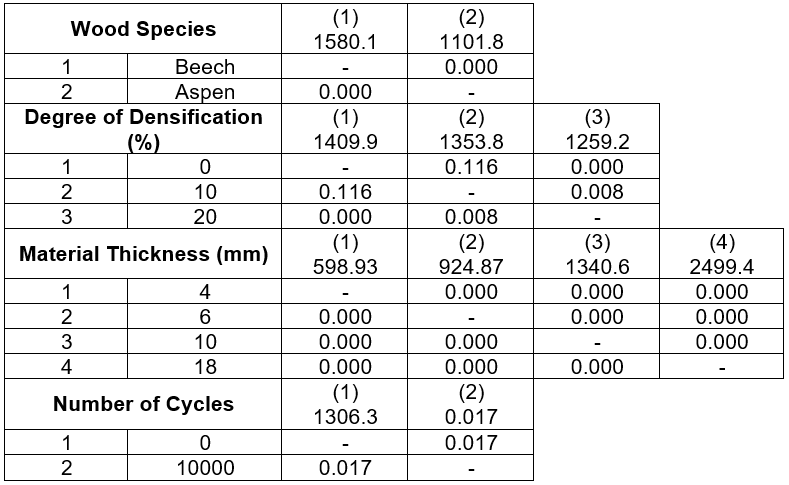
The results of Duncan’s test (Table 4) showed a significant effect of the wood species (P = 0.001), material thickness (P = 0.001), and number of cycles (P = 0.001) at all monitored levels. As the degree of densification increased, its effect on the values of the monitored characteristic also increased. At 10% densification the level of significance was P = 0.34, and at 20% densification the level of significance was P = 0.001.
Table 4. Comparison of the Effects of individual factors using Duncan Test on the force at the proportionality limit
The respective model explained roughly 94% of the total sum of squares on the force at the maximum limit (Table 5).
Table 5. Statistical Evaluation of the Effect of Factors and their Interaction on the Force at the Maximum limit
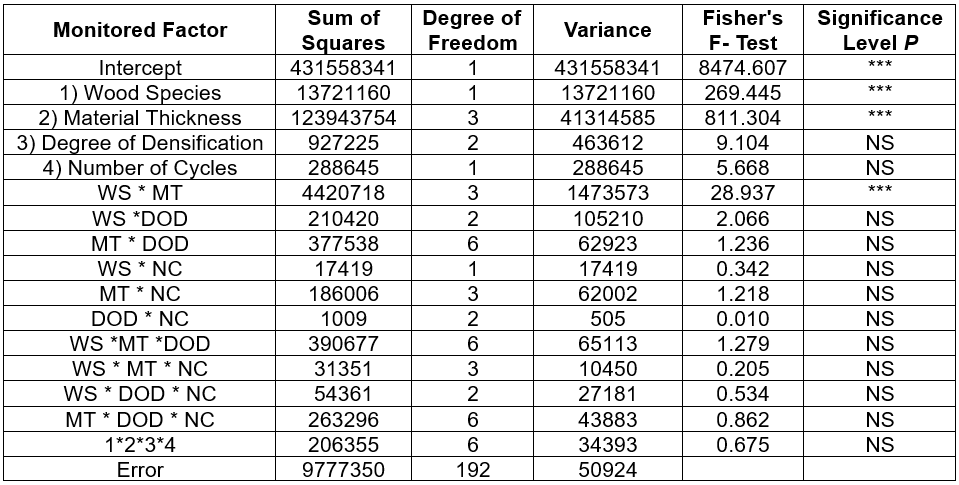
NS- not significant, ***- significant at p<0.005
The results of Duncan’s test (Table 6) showed a significant effect of all the monitored factors with a significance level of P = 0.001, with the exception of a 10% degree of densification, in which the significance level was P = 0.116.
Table 6. Comparison of the Effects of Individual Factors using Duncan Test on the Force at the Maximum limit
The average force at the proportionality limit was 38.3% (830 N) higher in beech wood than in aspen wood (600 N). In the case of the force at the maximum limit, the value 43.2% (15 900 N) was measured, which is higher in beech wood than in aspen wood (11100 N) (Fig. 5). These higher values of the forces measured in beech wood were the result of the effect of the wood structure and density. The average density of the beech wood (728 kg/m3) was 36.3% higher than that of aspen wood (534 kg/m3) (Table 2). The findings given above corresponded with the results of multiple authors who reported that increased density results in higher values of the mechanical properties, and therefore higher force under stress, which corresponds with the results of the work of (Gaff et al. 2015a; 2017).
A significant effect of the material thickness on the force at the proportionality limit and the force at the maximum limit was evident from the results shown in Fig. 6. Based on knowledge about the stress, which was defined by a proportion of the force “F” per surface unit, it was evident that the observed increase in the value of forces at the proportionality limit and at the maximum limit was due to a larger surface area. Percentage changes in the measured forces and surface area changes at various thicknesses of specimens are shown in Table 7.
Table 7. Average Parameter Values of the Bent Specimens
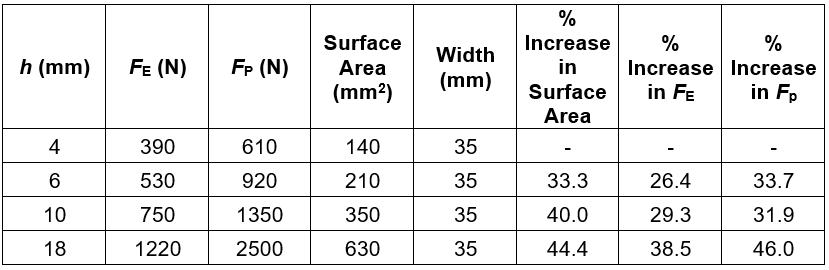
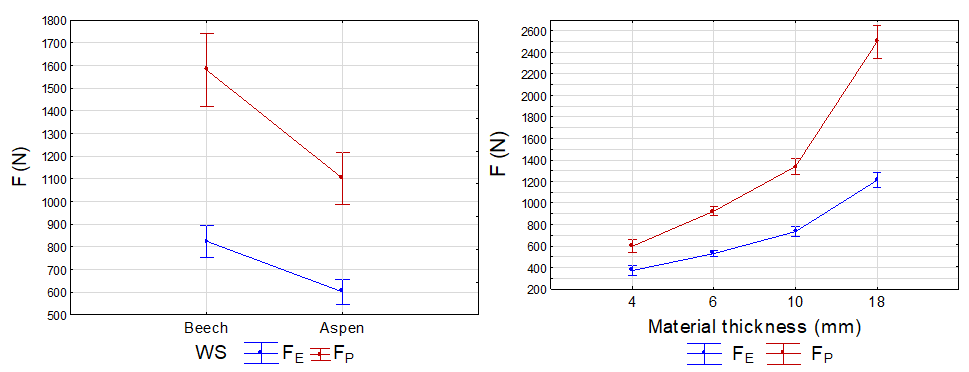
Fig. 5. Effect of the wood species on the force at the Fig. 6. Effect of the material thickness on the force at the
proportionality limit and maximum limit proportionality limit and maximum limit
The effect of the degree of densification of individual lamellas resulted in a decrease in the values of forces measured at the proportionality limit and at the maximum limit (Fig. 7). Although that decrease was not statistically significant, the authors will conduct further research on this phenomenon in the future and examine the effect of higher degrees of densification.
Cyclic loading caused the values of the forces measured at the proportionality limit and at the maximum limit to increase (Fig. 8). While this increase was not statistically significant at the monitored level of significance, the results of this work focused on assessing the limit of proportionality, which indicated cyclic loading may have resulted in an increase in values characterizing the limit of proportionality. Cyclic loading caused the development of plastic deformation, which resulted in a reduction in the non-linear region. Due to the loosening of bonds (caused by cyclic loading) between the components of lignin and cellulose, which form the main component of the wood’s strength, the maximum limit values increased (Požgaj et al. 1997; Higashihara et al. 2000; Yamashita et al. 2009). It could be said that the elasticity of the material increased with bending. It was likely that the monitored number of loading cycles exceeded the fatigue strength limit at a submicroscopic level.
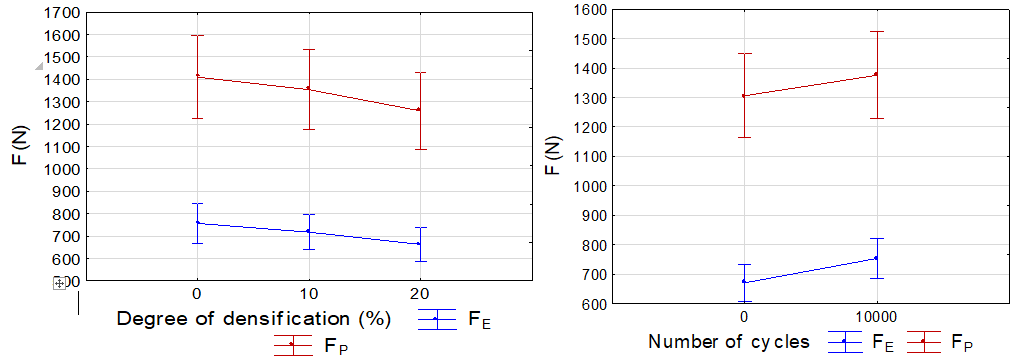
Fig. 7. Effect of the degree of densification on the force Fig. 8. Effect of the number of cycles on the force
at the proportionality limit and maximum limit at the proportionality limit and maximum limit
The synergistic effect of all the monitored factors on the force at the proportionality limit is shown in Figs. 9 and 10. The results indicated that the material thickness had the most significant effect on the monitored characteristic; a significant effect of the degree of densification was also observed.
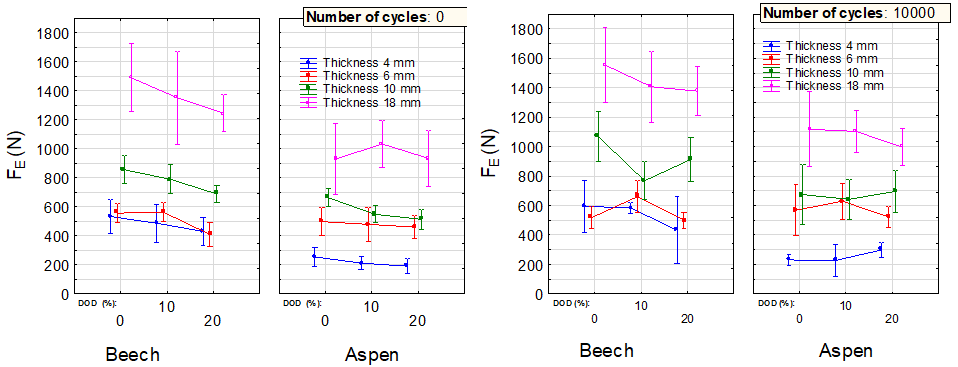
Fig. 9. Synergistic effect of the studied factors Fig. 10. Synergistic effect of the studied factors
on the force at the proportionality limit on the force at the proportionality limit
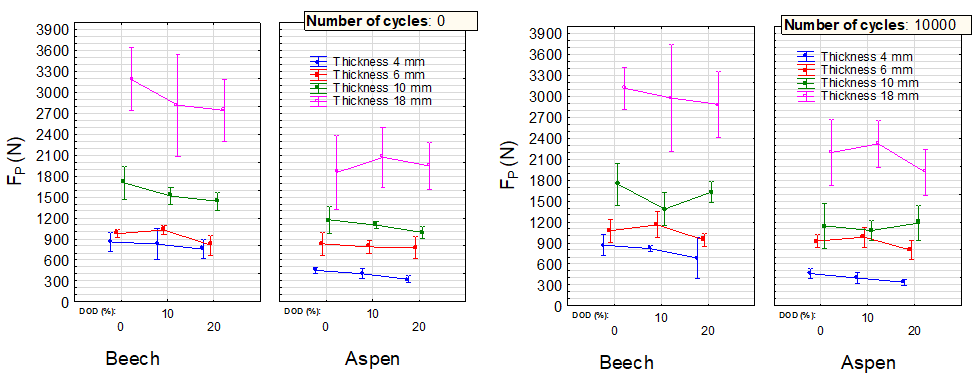
Fig. 11. Synergistic effect of the studied factors Fig. 12. Synergistic effect of the studied factors
on the force at the maximum limit on the force at the maximum limit
The synergistic effect of all four monitored factors on the force at the maximum limit is shown in Figs. 11 and 12. As was the case in the force at the proportionality limit, the material thickness and cyclic loading had the most significant effect.
Ratio of the Force at the Proportionality Limit and at the Maximum limit
The ratio of the force at the proportionality limit and the force at the maximum limit was significantly affected by each of the observed factors, except for the degree of densification, which was shown to be insignificant (Table 8). The synergistic effect of all the monitored factors was considered significant based on the results of the level of significance “P.” The respective model explained roughly 57% of the total sum of squares of their interaction on the force ratio.
Table 8. Statistical Evaluation of Factors and the Effect of their Interaction on the Force Ratio
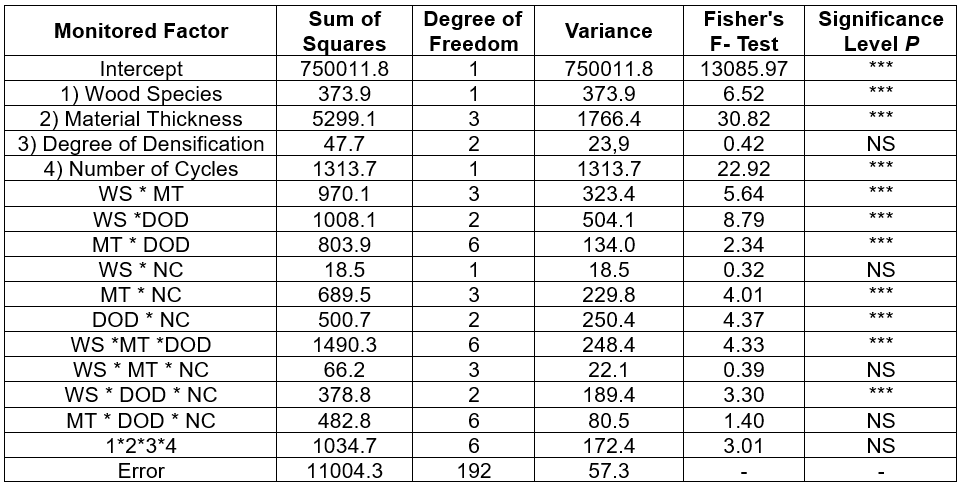
NS- not significant, ***- significant at p<0.005
The results of Duncan’s test (Table 9) showed a significant effect of the wood species with a significance level of P = 0.011; the number of cycles and material thickness had a significance level of P = 0.001. The results further showed that neither of the monitored degrees of densification had an effect on the force ratio (10% – P = 0.841, 20% – P = 0.502).
Table 9. Comparison of the Effects of Individual Factors using Duncan Test on the Values of the Force Ratio
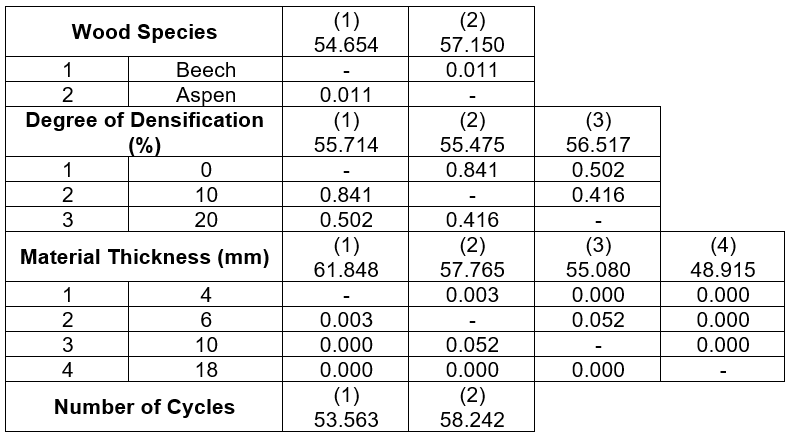
The results given in Fig. 13 show that aspen wood can be regarded as a material with a lower toughness than beechwood. A 4.6% higher force ratio was measured in aspen wood (54.6%) than in beechwood (57.2%).
Increased material thickness resulted in a significant increase in the forces required for deformation in the viscoplastic region (Fig. 14). The results showed that the toughness of the material increased with the thickness of the material, and its flexibility significantly decreased.
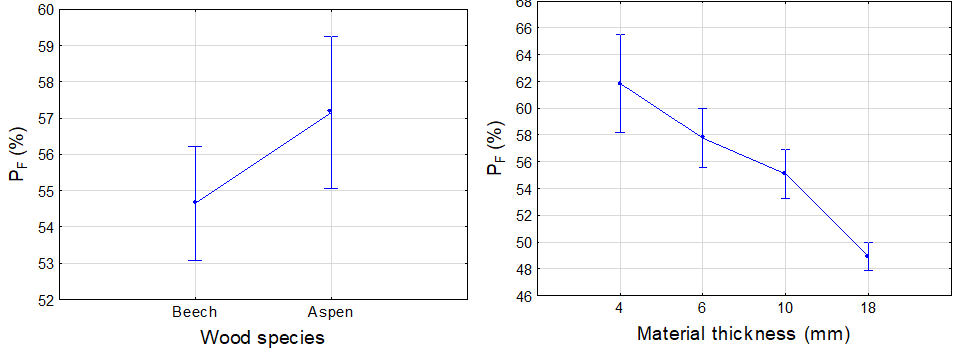
Fig. 13. The effect of the wood species on the force ratio Fig. 14. The effect of the material thickness on the force ratio
Cyclic loading caused a statistically significant increase in the ratio of the force at the proportional limit and the force at the maximum limit (Fig. 16). In specimens subjected to cyclic loading (58.2%), 4.7% higher values were measured than in specimens that were not subjected to cyclic loading (53.5%). It was believed that cyclic loading caused the development of plastic deformation, which resulted in a reduction in the non-linear region. The toughness of the monitored material decreased due to a loosening of hydrogen bonds at a microscopic level.The degree of densification within the monitored range of densification had a statistically insignificant effect on the force ratio (Fig. 15), which was confirmed by the probability results shown in Table 6.
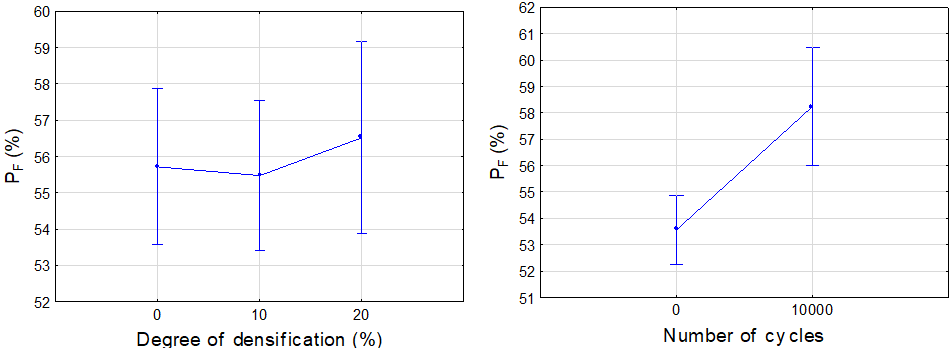
Fig. 15. The effect of the degree of densification on the force ratio Fig. 16. The effect of the number of cycles on the force ratio
The synergistic effect of all the monitored factors on the percentual force ratio during woodworking is shown in Figs. 17 and 18. Based on these results, it can be concluded that the material thickness had the greatest effect on changes in the monitored characteristic, followed by cyclic loading, and the wood species, which were confirmed by the F-test shown in Table 6.

Fig. 17. Synergistic effect of the studied factors on the force ratio Fig. 18. Synergistic effect of the studied factors on the force ratio
The degree of dependence between the force at the proportionality limit and the force at the maximum limit was 95% (Table 10). This suggested a close degree of dependence between the monitored characteristics.
Correlation Analysis
The level of significance of the force ratio and the force at the proportionality limit was only 21%, while the degree of dependence between the force ratio and the force at the proportionality limit was 46%. This indicated that the proportionality limit had an insignificant effect on the force ratio, while the maximum limit had a very significant effect on this characteristic.
Table 10. Spearman’s Correlation
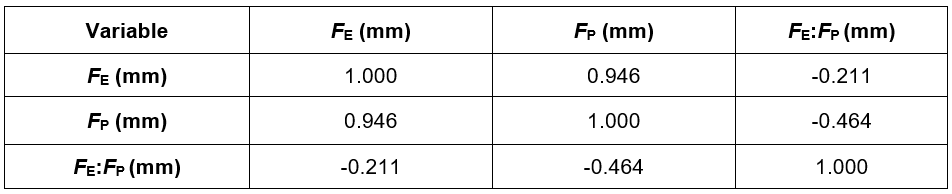
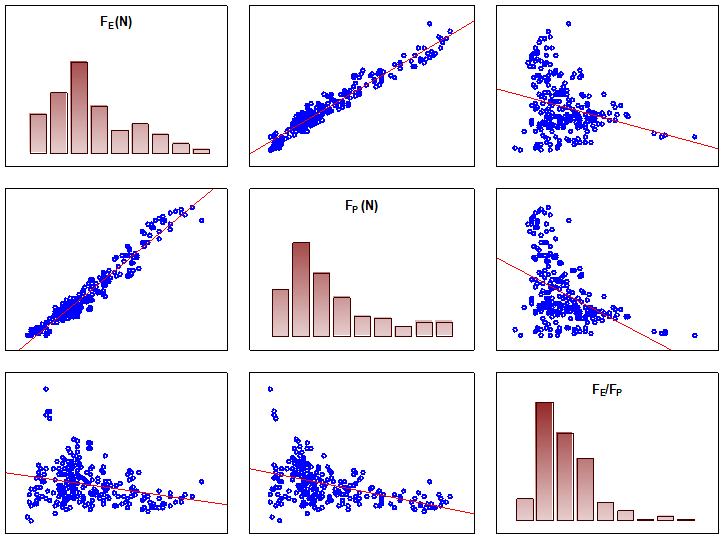
Fig. 19. Correlation matrix of the degree of dependence of the monitored characteristics
Future Effects of the Monitored Bending Characteristics on the Costs of the Innovated Technological Process and Product
From a management and economic point of view, the monitored characteristics, the force at the proportionality limit FE, and the force at the maximum limit FP in bending stress can be expected to affect the costs of the innovated technological process and product in the design of tools intended for the technological bending process.
Monitored properties and statistically validated correlations would also affect the resulting technological process, its changes, and the total costs associated with the technological bending process, such as depreciation of equipment, energy consumption, and other overhead costs associated with the technological tools used.
Conversely, the degree of densification as a quantity that has no significant effect on the final bending properties could be neutral in terms of future costs.
One will only be able to explicitly determine the overall changes in costs after the application of the results of this research and their use in future product innovation and innovation of the technological bending process. With the right combination of parameters, product innovation can be achieved in the future at lower costs, while maintaining their original structural properties, and ensuring the required product quality. The authors plan to follow these innovation objectives in their next research.
CONCLUSIONS
- By applying a method based on the evaluation of the force ratio, the properties of a material were evaluated, with emphasis on its future use and its properties under stress.
- The values of both monitored forces were significantly lower in aspen wood than in beech wood. Both monitored characteristics were significantly affected by an increase in surface area, as a result of which both characteristics increased significantly.
- The toughness of the materials tested was significantly affected by cyclic loading, as a result of which the toughness of the material decreased; as the surface area increased, the toughness also increased.
- The force ratio was largely influenced by the force at the maximum limit (46%), whereas the effect of the force at the proportionality limit was 21%. As the force at the maximum limit increased, the force ratio decreased.
- The critical characteristics that would affect the costs of the future technological process and the resulting innovated product include the wood species, material thickness, and number of cycles, in its practical use.
- With an optimal combination of these parameters in the innovation of the technological process and structural design of the product, lower costs and better economic parameters in the future would be able to be achieved.
ACKNOWLEDGMENTS
The authors are grateful for the support of the Grant Agency at the Faculty of Forestry and Wood Science, project No. A08/16.
REFERENCES CITED
Bezazi, A., and Scarpa, F. (2007). “Mechanical behavior of conventional and negative Poisson’s ratio thermoplastic polyurethane foams under compressive cyclic loading,” International Journal of Fatigue 29(5), 922-930. DOI: 10.1016/j.ijfatigue.2006.07.01
Blomberg, J., Persson, B., and Blomberg, A. (2005). “Effects of semi-isostatic densification of wood on the variation in strength properties in density,” Wood Science and Technology 39(5), 339-350. DOI: 10.1007/s00226-005-0290-8
Bodig, J., and Jayne, B. A. (1982). Mechanics of Wood and Wood Composites, Van Nostran-Reinhold Co., Inc., New York, NY, pp. 712.
Chromjaková, F., and Rajnoha, R. (2009). “Ekonomika inovácie ako súčasť zvyšovania výkonnosti firmy [Economy of innovation as a part of the increase of the company performance],” Journal of Competitiveness 1(1), 66-74. DOI: http://www.cjournal.cz/files/7.pdf (http://www.wsl.ch/dienstleistungen/publikationen/pdf/12494.pdf), 14 February 2017.
Eilmann, B., Sterck, F., Wegner, L., de Vries, S. M. G., Von Arx, G., Mohren, G. M. J., den Ouden, J., and Sass-Klaassen, U. (2014). “Wood structural differences between northern and southern beech provenances growing at a moderate site,” Tree Physiology 34(8), 882-893. DOI: 10.1093/treephys/tpu069
EN 310 (1993). “Wood-based panels – Determination of modulus of elasticity in bending and of bending strength,” European Committee for Standardization, Brussels, Belgium.
Fortino, S., Genoese, A., Genoese, A., and Rautkari, L. (2013). “FEM simulation of the hygro-thermal behavior of wood under surface densification at high temperature,” Journal of Materials Science 48(21), 7603-7612. DOI: 10.1007/s10853-013-7577-1
Gaff, M., Gašparík, M., Baiak, M., and Vokatý, V. (2017). “Bendability characteristics of wood lamellae in plastic region,” Composite Structures 163, 410-422. DOI: 10.1016/j.compstruct.2016.12.052
Gaff, M., Gašparík, M., Borůvka, V., and Haviarová, E. (2015a). “Stress simulation in layered wood-based materials under mechanical loading,” Materials and Design 87, 1065-1071. DOI: 10.1016/j.matdes.2015.08.128
Gaff, M., Vokatý, V., Baiak, M., and Vokatý, V. (2016). “Coefficient of wood bendabitily as a function of selected factors,” Construction and Building Materials 126, 632-640. DOI: 10.1016/j.conbuildmat.2016.09.085
Gašparík, M., and Gaff, M., (2015a). “The influence of cyclic stress on the attenuation rate of deflection of solid wood and laminated wood,” Wood Research 60(3), 351-358.
Gašparík, M., and Gaff, M., (2015b). “Influence of densification on bending strength of beech wood,” Wood Research 60 (2), 211-218.
Higashihara, T., Morooka, T., and Norimoto, M. (2000). “Permanent fixation of transversely compressed wood by heating and its mechanism,” Mokuzai Gakkaishi 52(4), 291-297.
Igaz, R., Krišťák, Ľ., Ružiak, I., Réh, R., and Danihelová, Z. (2016). “Heat transfer during pressing of 3D moulded veneer plywood composite materials,” Key Engineering Materials 688, 131-137. DOI:10.4028/www.scientific.net/KEM.688.131
Igaz, R., Ružiak, I., Krišťák, Ľ., Réh, R., Iždinský, J. and Šiagiová, P. (2015). “Optimization of pressing parameters of crosswise bonded timber formwork sheets,” Acta Facultatis Xylologiae Zvolen 57(1), 83-88.
ISO 13061-1 (2014). “Wood-determination of moisture content for physical and mechanical tests,” International Organization for Standardization, Geneva, Switzerland.
ISO 13061-2 (2014). “Wood-determination of density for physical and mechanical tests,” International Organization for Standardization, Geneva, Switzerland.
ISO 3348 (1975). “Wood-determination of impact bending strength,” International Organization for Standardization, Geneva, Switzerland.
Kamke, F. A. (2006). “Densified radiata pine for structural composites,” Maderas Ciencia y Tecnología 8(2), 83-92. DOI: 10.4067/S0718-221X2006000200002
Mackes, K. H., and Lynch, D. L. (2001). “The effect of aspen wood characteristics and properties on utilization,” in: Sustaining Aspen in Western Landscapes: Symposium Proceedings June 2000, Grand Junction, CO, pp. 429-440.
Požgaj, A., Chovanec, D., Kurjatko, S., and Babiak, M. (1997). Štruktúra a Vlastnosti Dreva [Structure and Properties of Wood], Príroda A. S., Bratislava, Slovakia.
Rajnoha, R., and Lorincová, S. (2015). “Strategic management of business performance based on innovations and information support in specific conditions of Slovakia,” Journal of Competitiveness 7(1), 3-21. DOI: 10.7441/joc.2015.01.01
Ružiak, I., Igaz, R., Krišťák, Ľ., Réh, R., Mitterpach, J., Očkajová, A., and Kučerka, M. (2017). “Influence of urea-formaldehyde adhesive modification with beech bark on chosen properties of plywood,” Bioresources 12(2), 3250-3264. DOI: 10.15376/biores.12.2.3250-3264.
Sandberg, D., and Navi, P. (2007) Introduction to Thermo-hydro-mechanical (THM) Wood Processing, Master’s Thesis, School of Technology and Design, Växjö University, Växjö, Sweden.
Sandberg, D., Haller, P., and Navi, P. (2013). “Thermo-hydro and thermo-hydro-mechanical wood processing: An opportunity for future environmentally friendly wood products,” Wood Material Science & Engineering 8(1), 64-88. DOI: 10.1080/17480272.2012.751935
Schellberg, D. (2012). Innovativer Möbelbau – Aktuelle Materialien und Techniken. Gebundenes Buch mit Schutzumschlag [Current Materials and Techniques. Hardcover book with protective cover] Deutsche Verlags-Anstalt, München, Germany.
Wagenführ, R. (2000). Holzatlas [Atlas of Wood] 5th Edition, Fachbuchverlag, Leipzig, Germany.
Wagenfuhrer, A., Buchelt, B., and Pfriem, A. (2006). “Material behaviour of veneer during multidimensional molding,” Holz als Roh-und Werkstoff 64, 83-89. DOI: 10.1007/s00107-005-0008-5
Wiemann, M. C. (2010). “Characteristics and availability of commercially important Woods,” in: Wood Handbook-Wood as an Engineering Material, Centennial edition, Forest Product Laboratory, Madison, WI, USA, pp. 508.
Yamashita, O., Yokochi, M., Miki, T., and Kanayama, K. (2009). “The pliability of wood and its application to molding,” Journal of Materials Processing Technology 209(12-13), 5239-5244. DOI: 10.1016/j.jmatprotec.2008.12.011
Article submitted: January 4, 2017; Peer review completed: April 13, 2017; Revised version received and accepted: April 15, 2017; Published: April 24, 2017.
DOI: 10.15376/biores.12.2.4146-4165
