Abstract
Phyllostachys edulis bamboo is one of the most valuable bamboo species in the world. It has the following advantages: high strength, light weight, and green, renewable character. In addition, it has a broad application prospect under the background of developing green buildings all over the world. The moisture content and density are the key factors affecting the mechanical properties of bamboos. However, there is no two-variable model of the mechanical properties with respect to the moisture content and density of P. edulis bamboo. In this paper, analysis of the compression parallel to the grain, bending, tensile parallel to the grain, and shear parallel to the grain of P. edulis bamboo were performed. The relationship between the mechanical properties and the moisture content and density was fitted by a two-variable model. The results show that the two-variable model has good fitting effect. As such, the two-variable model can be used to predict the mechanical properties of P. edulis bamboo according to its moisture content and density.
Download PDF
Full Article
A Two-variable Model for Predicting the Effects of Moisture Content and Density on the Mechanical Properties of Phyllostachys edulis Bamboo
Pengcheng Liu, Qishi Zhou,* and Jiefu Tian
Phyllostachys edulis bamboo is one of the most valuable bamboo species in the world. It has the following advantages: high strength, light weight, and green, renewable character. In addition, it has a broad application prospect under the background of developing green buildings all over the world. The moisture content and density are the key factors affecting the mechanical properties of bamboos. However, there is no two-variable model of the mechanical properties with respect to the moisture content and density of P. edulis bamboo. In this paper, analysis of the compression parallel to the grain, bending, tensile parallel to the grain, and shear parallel to the grain of P. edulis bamboo were performed. The relationship between the mechanical properties and the moisture content and density was fitted by a two-variable model. The results show that the two-variable model has good fitting effect. As such, the two-variable model can be used to predict the mechanical properties of P. edulis bamboo according to its moisture content and density.
DOI: 10.15376/biores.17.1.400-410
Keywords: Phyllostachys edulis bamboo; Mechanical properties; Fitting; Prediction
Contact information: School of Civil Engineering, Central South University, Changsha, Hunan Province 410075 China; *Corresponding author: qishizhou@csu.edu.cn
GRAPHICAL ABSTRACT

INTRODUCTION
Bamboo is the fastest growing plant on Earth, taking approximately 4 years to grow (Shastry and Unnikrishnan 2017; Skuratov et al. 2021). Bamboo is primarily distributed in the Asia-pacific region, Africa region, and the Americas region. Among them, the Asia-pacific region has the most bamboo species and quantity, especially China. In China, bamboo is primarily distributed in Zhejiang, Hunan, Jiangxi, and other provinces, and Phyllostachys edulis bamboo has the widest distribution, the largest amount, and the most applications in engineering. Compared with the scarcity of wood resources, bamboo is very abundant; it also has the following advantages: high strength and rigidity, light weight; and good toughness (Liu et al. 2014; Osorio et al. 2018; Zhang et al. 2019; Gauss et al. 2020; Wang and Shao 2020).
As environmental pollution is becoming more and more serious, and the construction industry accounts for the highest proportion of CO2 emissions, more and more countries and international organizations are calling for and issuing relevant policies to promote the development of green buildings (Jose and Bhirud 2018; Kieu and Schäfer 2020; Hu and Skibniewski 2021). As such, bamboo is more and more widely used in green buildings. The ‘ZCB Bamboo Pavilion’ (Crolla 2017) is a public event space capable of seating 200 people. It is a bending-active gridshell structure that spans 37 meters, is more than 10 meters high, and is wrapped in a lightweight translucent glass-fibre reinforced polymer membrane. Bamboo can also be designed as a truss structure (Paraskeva et al. 2017), which consists of bamboo tubes and strips connected by steel clamps. The experimental results show that the truss structure can be used for low cost and prefabricated floor slabs and rooves. Bamboo can also be used to make bridges (Xiao et al. 2014), which have broad application prospects in rural and landscape areas.
In order to promote the application of bamboo in architecture, the mechanical properties must be clearly understood. It is of great importance to predict the mechanical properties of bamboo. Presently, research on the prediction of the mechanical properties of bamboo is very limited; most studies are for the prediction for a certain type of mechanical property, and the prediction indexes used are mostly one-variate. For example, Ribeiro et al. (2017) carried out bending tests on bamboo stalks and obtained the relationship between the bending strength and bending elastic modulus. Dixon and Gibson (2014) studied the relationship between axial compressive performance and density of P. edulis bamboo and fit it using a linear function. Javadian et al. (2019) established a prediction model for tensile strength using the diameter of Petung Putih bamboo.
In the prediction indexes of bamboo, density has the strongest correlation with the mechanical properties theoretically (Lo et al. 2004; Bahtiar et al. 2019). At the same time, the effect of the moisture content on the mechanical properties of bamboo is very important (Xu et al. 2014; Chen et al. 2018; Jakovljević and Lisjak 2019). It can be considered that density is the property of bamboo itself, and water content is related to the external environment. Therefore, it is of great importance to use the moisture content and density to predict the mechanical properties of bamboo. The established prediction formula can be used to predict the mechanical properties of bamboo by using the physical properties of bamboo. Such an approach which will save a lot of specimens and material costs for mechanical properties test of bamboo. This type of study has important reference value for promoting the application of bamboo structure.
In order to predict the mechanical properties of bamboo, the following tasks were carried out in this paper: (1) tests of the compression parallel to the grain, bending, tensile parallel to the grain, and shear parallel to the grain of Chinese P. edulis bamboo were carried out, and the failure modes and process of bamboos were analyzed. (2) The prediction formulas of mechanical properties and physical properties were proposed, and the relationship between mechanical properties and two physical properties was fitted.
EXPERIMENTAL
Materials
A total of 25 samples of 4-year-old P. edulis bamboo with a length of 6 m were cut in Chenzhou City, Hunan Province, China. In order to avoid the splitting of the bamboo stalk caused by logging, the cutting position was near the bottom node. After the bamboo stalks were air-dried, four types of specimens were made, i.e., compression parallel to the grain (UC), bending (B), tensile parallel to the grain (UT) and shear parallel to the grain (US), which were distributed uniformly and circulative along the height direction of the bamboo stalks. As shown in Fig. 1, the ratio of the height and diameter of UC and US specimens was 1, according to JG/T standard 199 (2007) and ISO standard 22157-1 (2019). The size of the B specimens was 220 mm × 15 mm × t mm (where t is the wall thickness), and the size of UT specimens was 330 mm × 15 mm × t mm, according to JG/T standard 199 (2007) and ISO standard 22157-1 (2019). After the mechanical property tests, a small specimen, with the size of approximately 20 mm × 20 × t mm, was removed near the failure location to carry out the moisture content and density tests.
Fig. 1. Schematic diagram of the specimen
Physical and Mechanical Properties
The mechanical properties were tested using an ETM504C universal testing machine (Shenzhen Wancai Test Equipment Co., Ltd., Shenzhen, China). According to JG/T199 (2007) and ISO 22157-1 (2019), the loading rate of the UC, US and UT samples was 0.01 mm/s, and the loading rate of the B samples was 150 N/mm2 per min. The calculation formula of the mechanical properties, moisture content and density are shown in Eqs. 1 through 6,
where MC is the air dry moisture content (%); ƒ is the strength (MPa) of the UC, US, and UT specimens; E is the elastic modulus (GPa) of the UC and UT specimens; MOR is the bending strength (MPa); MOE is the flexural elastic modulus (GPa); Pmax is failure load (N); A is the stressed area (mm2); t is the thickness of the specimen (mm); b is the height of the specimen (mm); P is the difference between the upper and lower loads (N); ∆l is the difference (mm) in specimen deformation under the function of the upper and lower loads; δm is the deflection value (mm) of the pure bending section of the specimen under the action of ∆P; m1 and m0 are the mass (g) of the gas dry and full dry, respectively; ρ is the density (g/cm3); and V is the dry gas volume (cm3), which was measured via the drainage method.
Data Analysis
The commercial statistical software Origin (Version 8.0, Originlab Co., Northampton, MA) was used to analyze the data, and important statistical indicators, e.g., the mean value, maximum value, minimum value, and standard difference of mechanical properties were obtained. Nonlinear surface fitting was carried out for the mechanical properties by adopting the moisture content and density, and the Poly function, as shown in Eq. 7,
where z0, a, b, c, d, and e are parameters.
The determination coefficient (R2) was used as the index to measure the fitting effect. R2 is the ratio of the regression sum of squares to the total sum of squares, i.e., the percentage of the dependent variable variability that can be explained by the regression formula. The value range of R2 is [0,1]. The larger the value is, the better the fitting effect is. If R2 is greater than 0.7, it indicates a good correlation.
RESULTS AND DISCUSSION
Mechanical Performance Statistics
The compressive strength parallel to the grain (UCS), compressive elastic modulus parallel to the grain (UCE), flexural strength (MOR), flexural elastic modulus parallel to the grain (MOE), tensile strength parallel to the grain (UTS), tensile elastic modulus parallel to the grain (UTE), and shear strength parallel to the grain (USS) of the bamboo samples were calculated (as shown in Table 1), and the probability distribution is shown in Fig. 2. It can be seen from Table 1 that the mechanical properties of the bamboo samples show typical anisotropic characteristics, and the UTS is the highest among these mechanical properties. Figure 2 shows that all the mechanical properties conform to a normal distribution.
Table 1. Mechanical Performance Statistics
Destruction Process and Destruction Pattern
The failure modes of various mechanical properties of bamboo specimens include ductile failure and brittle failure. The test types of mechanical properties for ductile failure include tensile and bending resistance parallel to the grain, and those for brittle failure include tensile and shear resistance parallel to the grain. Typical load-displacement curves obtained from various mechanical properties tests are shown in Fig. 3, and failure modes are shown in Fig. 4. The load-displacement curve of UC specimen can be divided into three stages: elastic section, elastic-plastic section, and failure section. In the elastic section, the load of the specimen increases linearly with the increase of the displacement, and no damage occurs to the bamboo at this time. With the increase of load, the load-displacement curve changes from linear to nonlinear.
Fig. 2. Probability distribution of the mechanical properties
Compared with the elastic section, the increase of specimen displacement increases gradually with the same load. At this stage, the specimen gradually produces visible buckling deformation. In the failure stage, the specimen was broken due to continuous cracks in the fiber direction (Fig. 4a). The plastic platform of load-displacement curve of the B specimen was obviously shorter than that of the UT specimen. During the loading process, the specimen gradually deformed in flexure and was finally destroyed by fiber fracture in pure bending section (Fig. 4b). The load-displacement curves of UT and US specimens generally showed linear characteristics, that is, the specimens failed without warning. As can be seen from the failure picture, UT specimen fractured in the middle horizontal plane (Fig. 4c), while US specimen failed due to dislocation in the shear plane (Fig. 4d).
In order to better compare the ductility of various specimens, the ductility coefficient of load-displacement curve in Fig. 1 is calculated in Table 1. Table 1 shows that the ductility coefficient of UC specimen reached 2.47, which was the highest among all specimens. B specimen and UT specimen were the next. The ductility coefficient of the US specimen was 0.73, which was the lowest among all specimens. In summary, in the four types of tests of compression resistance, bending resistance, tension resistance and shear resistance parallel to the grain, the compression ductility parallel to the grain was the highest, and the tensile ductility parallel to the grain is the lowest.
Fig. 3. Typical load-displacement curves
Fig. 4. Typical damage pattern
Table 1. Ductility Coefficient Statistics
Two-variable Model of the Mechanical Properties Considering the Moisture Content and Density
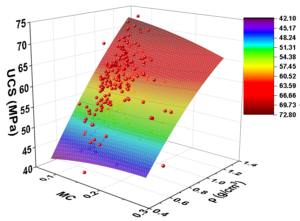
The fitted surface is shown in Fig. 5, and for each mechanical property, the corresponding fitting parameters of the moisture content and density were statistically analyzed (Table 2). It can be seen from Fig. 5 and Table 2 that among the 7 mechanical properties, the R2 value of UCS, UCE, and UTE fitted with the two physical properties was greater than 0.7, indicating that the above three mechanical properties had a good correlation with water content and density. The R2 values of UTS, MOR, MOE and USS fitted with the two physical properties were slightly less than 0.7. The mean R2 value of 7 mechanical and physical properties was 0.7. UTE had the highest fitting correlation, and MOE had the lowest.
Since the mechanical properties of bamboo cannot be obtained at the same time through the testing of one specimen, using Eq. 7 and the parameters in Table 2, the moisture content and density can be used to predict multiple mechanical properties of bamboo. The results of this paper will improve the efficiency of the prediction of the mechanical properties of P. edulis bamboo in terms of the test and time costs.
Fig. 5. Fitting surface of the mechanical properties, moisture content, and density
Table 2. Fitting Parameters
In this work, analysis of the compression parallel to the grain, bending, tensile parallel to the grain, as well as shear parallel to the grain of P. edulis bamboo was performed. In addition, two-variable models of the compressive strength parallel to the grain, compressive elastic modulus parallel to the grain, flexural strength, flexural elastic modulus, tensile strength parallel to the grain, tensile elastic modulus parallel to the grain, shear strength parallel to the grain, and moisture content and density were fitted by the polynomial functions. The main conclusions are as follows:
- The failure of bamboo is divided into ductile failure and brittle failure. The compressive and bending resistance parallel to the grain show ductile failure characteristics, while the tensile and shear resistance parallel to the grain show brittle failure characteristics.
- Among the 7 mechanical properties of bamboo, the fitting coefficients of compressive strength parallel to the grain, compressive elastic modulus parallel to the grain and tensile elastic modulus parallel to the grain with water content and density are greater than 0.7. That is, they have a good correlation with water content and density. The correlation between tensile elastic modulus along grain and two physical properties is the best, while flexural elastic modulus is the worst.
- The two-variable model in this study can predict the mechanical properties of P. edulis bamboo by its moisture content and density, which will strongly promote the application of bamboo in engineering.
ACKNOWLEDGMENTS
The work described in this research was supported by grants from the National Key R&D Program of China (Grant No. 2017YFC0703500).
Conflict of Interest Statement
The authors declare that they have no conflict of interest.
Supplementary Materials
Underlying research materials related to this research can be accessed on request from the corresponding author.
REFERENCES CITED
Bahtiar, E. T., Imanullah, A. P., Hermawan, D., Nugroho, N., and Abdurachman. (2019). “Structural grading of three sympodial bamboo culms (Hitam, Andong, and Tali) subjected to axial compressive load,” Engineering Structures 181, 233-245. DOI: 10.1016/j.engstruct.2018.12.026
Chen, G., Luo, H., Yang, H., Zhang, T., and Li, S. (2018). “Water effects on the deformation and fracture behaviors of the multi-scaled cellular fibrous bamboo,” Acta Biomaterialia 65, 203-215. DOI: 10.1016/j.actbio.2017.10.005
Crolla, K. (2017). “Building indeterminacy modelling – the ‘ZCB Bamboo Pavilion’ as a case study on nonstandard construction from natural materials,” Visualization in Engineering 5(1). DOI: 10.1186/s40327-017-0051-4
Dixon, P., and Gibson, L. (2014). “The structure and mechanics of Moso bamboo material,” Journal of The Royal Society Interface 11(99), 1-12. DOI: 10.1098/rsif.2014.0321
Gauss, C., Harries, K. A., Kadivar, M., Akinbade, Y., and Savastano, H. (2020). “Quality assessment and mechanical characterization of preservative-treated Moso bamboo (P. edulis),” European Journal of Wood and Wood Products 78(2), 257-270. DOI: 10.1007/s00107-020-01508-x
Hu, M., and Skibniewski, M. (2021). “A review of building construction cost research: Current status, gaps and green buildings,” Green Building and Construction Economics 2(1), 1-17. DOI: 10.37256/gbce.212021768
ISO 22157 (2019). “Bamboo structures — Determination of physical and mechanical properties of bamboo culms — Test methods,” International Organization for Standardization, Geneva, Switzerland.
Jakovljević, S., and Lisjak, D. (2019). “Investigation into the effects of humidity on the mechanical and physical properties of bamboo,” Construction and Building Materials 194, 386-396. DOI: 10.1016/j.conbuildmat.2018.11.030
Javadian, A., Smith, I. F. C., Saeidi, N., and Hebel, D. E. (2019). “Mechanical properties of bamboo through measurement of culm physical properties for composite fabrication of structural concrete reinforcement,” Frontiers in Materials 6, 1-18. DOI: 10.3389/fmats.2019.00015
JG/T 199 (2007). “Test method for physical and mechanical properties of bamboo for construction,” Ministry of Construction of the People’s Republic of China, Beijing, China.
Jose, J., and Bhirud, A. (2018). “Green materials – Future of construction,” Journal of Advances and Scholarly Research in Allied Education 15(2), 589-592. DOI: 10.29070/15/56908
Kieu, L. T., and Schäfer, S. (2020). “A review of values of green building at building and city scales,” Green Building and Construction Economics 1(1), 37-50. DOI: 10.37256/gbce.112020620
Liu, H., Jiang, Z., Zhang, X., Liu, X., and Sun, Z. (2014). “Effect of fiber on tensile properties of Moso bamboo,” BioResources 9(4), 6888-6898. DOI: 10.15376/biores.9.4.6888-6898
Lo, T. Y., Cui, H. Z., and Leung, H. C. (2004). “The effect of fiber density on strength capacity of bamboo,” Materials Letters 58(21), 2595-2598. DOI: 10.1016/s0167-577x(04)00214-9
Osorio, L., Trujillo, E., Lens, F., Ivens, J., Verpoest, I., and Vuure, A. W. V. (2018). “In-depth study of the microstructure of bamboo fibres and their relation to the mechanical properties,” Journal of Reinforced Plastics and Composites 37(17), 1099-1113. DOI: 10.1177/0731684418783055
Paraskeva, T., Grigoropoulos, G. and Dimitrakopoulos, E. (2017). “Design and experimental verification of easily constructible bamboo footbridges for rural areas,” Engineering Structures 143, 540-548. DOI: 10.1016/j.engstruct.2017.04.044
Ribeiro, R. A. S., Ribeiro, M. G. S., and Miranda, I. P. A. (2017). “Bending strength and nondestructive evaluation of structural bamboo,” Construction and Building Materials 146, 38-42. DOI: 10.1016/j.conbuildmat.2017.04.074
Shastry, A., and Unnikrishnan, S. (2017). “Investigation on elastic properties of bamboo and behavior of bamboo reinforced concrete beams,” International Journal of Earth Sciences and Engineering 10(2), 304-312. DOI: 10.21276/ijee.2017.10.0223
Skuratov, S., Danilova-Volkovskaya, G., Yanukyan, E., and Beilin, M. (2021). “Bamboo as a unique ecological building material of the XXI century: Bamboo description, bamboo physical and mechanical properties studies,” Materials Science Forum 1043, 149-154. DOI: 10.4028/www.scientific.net/msf.1043.149
Wang, F., and Shao, Z. (2020). “Study on the variation law of bamboo fibers’ tensile properties and the organization structure on the radial direction of bamboo stem,” Industrial Crops and Products 152, 1-6. DOI: 10.1016/j.indcrop.2020.112521
Xiao, Y., Zhou, Q. and Shan, B. (2010). “Design and construction of modern bamboo bridges,” Journal of Bridge Engineering 15(5), 533-541. DOI: 10.1061/(asce)be.1943-5592.0000089
Xu, Q., Harries, K., Li, X., Liu, Q., and Gottron, J. (2014). “Mechanical properties of structural bamboo following immersion in water,” Engineering Structures 81, 230-239. DOI: 10.1016/j.engstruct.2014.09.044
Zhang, T., Wang, A., Wang, Q., and Guan, F. (2019). “Bending characteristics analysis and lightweight design of a bionic beam inspired by bamboo structures,” Thin-Walled Structures 142, 476-498. DOI: 10.1016/j.tws.2019.04.043
Article submitted: September 24, 2021; Peer review completed: November 6, 2021; Revised version received and accepted: November 14, 2021; Published: November 22, 2021.
DOI: 10.15376/biores.17.1.400-410
