Biodegradation properties of wood-plastic composites containing high content of lignocellulosic filler and zinc borate exposed to two different brown-rot fungi

Altuntas, E., Yilmaz, E., Salan, T., and Alma, M. H. (2017). "Biodegradation properties of wood-plastic composites containing high content of lignocellulosic filler and zinc borate exposed to two different brown-rot fungi," BioRes. 12(4), 7161-7177.

Abstract

The decay resistance of zinc borate-reinforced wood-plastic composites (WPCs) was studied against two types of brown-rot fungi (Rhodonia placenta and Coniophora puteana). The WPCs with 70% wood fibers (Pinus sylvestris L.) were reinforced with 1% and 2% zinc borate. The reinforced WPCs were exposed to a decay test according to the EN 113 (1996) standard. The composite samples were characterized by their weight losses and water absorption capacity (WAC) as well as by Fourier transform infrared spectroscopy (FTIR), scanning electron microscopy (SEM), thermogravimetric analysis (TGA), and differential thermal analysis (DTA). The weight losses and WAC results showed that zinc borate improved the decay resistance of the WPCs to a certain degree against brown rot fungi. The FTIR and SEM results showed that the brown rot fungi attacked the WPCs. It was concluded that the use of 1-2% zinc borate provided resistance to fungal attack on WPCs to a certain degree.

Download PDF

Full Article

Biodegradation Properties of Wood-plastic Composites Containing High Content of Lignocellulosic Filler and Zinc Borate Exposed to Two Different Brown-Rot Fungi

Ertugrul Altuntas,^a,* Esra Yilmaz,^a Tufan Salan,^b and Mehmet Hakki Alma ^a

Keywords: Wood-plastic composite; Zinc borate; High content filler; Fungal decay; Resistance

Contact information: a: Department of Forest Biology and Wood Protection Technology, Forestry Faculty, Kahramanmaras Sutcu Imam University, Kahramanmaras, Turkey; b: Department of Materials Science and Engineering, Kahramanmaras Sutcu Imam University, Kahramanmaras, Turkey;

* Corresponding author: ertugrulaltuntas@gmail.com

INTRODUCTION

Wood-plastic composites (WPCs) have been used recently in different construction and building applications such as decking, siding, benches, auto parts, and fencing. The lignocellulosic filling used in the WPCs is easily available and less expensive than other fillers. Wood-plastic composites have many advantages, such as lower resin costs, improved stiffness, and dimensional stability. Composites reinforced with lignocellulosic waste can reduce the use of petroleum-based plastics ( Ozdemir et al. 2014). The addition of wood significantly improves thermal stability, mechanical (stiffness), and working properties of the WPCs. The disadvantages of using wood fibers are dimensional stability, high tendency to absorb moisture, and susceptibility to fungal attack (Clemons 2002). Although plastics are normally resistant to fungal decay, a major concern with WPCs materials is that using lignocellulosic filling in the composite makes the material open to biological degradation (Lomeli-Ramirez et al. 2009).

Initially, it was assumed that plastics used in wood-plastic composites encapsulated lignocellulosics against wetting and decay. However, later many studies showed that the lignocellulosic entities were not completely encapsulated by the plastics. Thus, the lignocellulosics found in WPCs are susceptible to fungal decay (Naghipour 1997; Morris and Cooper 1998; Silva et al. 2007; Farahani and Banikarim 2013). Zinc borate has multifunctional properties as a fire retardant and fungal decay in WPCs manufacturing. Furthermore, zinc borate is a low-cost material for composite production. It is also thermally stable, with a decomposition temperature of approximately 300 °C (Klyosov 2007). The amount of lignocellulosic material in wood-plastic composites cannot exceed a certain amount for many reasons. One of the reasons is that it allows for the biodegradation and flammability of wood (Turku et al.2014).

There is limited research data concerning the effects of brown-rot fungi on WPCs, and more research is needed in this area. The purpose of this study was to determine an inexpensive way to solve the problem of fungal damage to WPCs that contain high amounts of lignocellulosic material. By choosing a WPCs formulation with a high wood ﬁller content, the goal was to observe unambiguously the differences and phenomena take place in the composite structure after fungal decay. The authors’ approach was to reinforce WPCs that consisted of 70% wood fiber with 1% and 2% zinc borate to investigate the fungal decay characteristics of a composite with a high content of biodegradable filler. The influence of zinc borate on the weight losses and WAC of the WPCs were studied, and the structural changes in composite samples were identified by using FTIR, TG/DTA and SEM.

EXPERIMENTAL

Materials

The fibers obtained from timber wastes (Pinus sylvestris L.) from a lumber mill (Veziroglu Co., Kahramanmaras, Turkey) were separated into 60-mesh fibers using screens, and the fibers were dried at 103 ºC before the manufacturing process. High-density polyethylene (HDPE, density: 0.965 g/cm³) and paraffin wax, which was used as a lubricant during extrusion, were provided by the Petkim Petrochemical Co. (Izmir, Turkey). Zinc borate (ZnO•2B₂O₃•3.5H₂O) was obtained from the Aromos Chemistry Co. (Izmir, Turkey).

Methods

The oven-dried fiber, HDPE, and zinc borate were prepared according to Table 1 to produce the composite materials.

Table 1. Weight Percentages of Wood-plastic Composites

Zinc borate concentrations of 1% and 2% were used against the brown fungi attack in the WPCs. The prepared materials were homogeneously mixed with a high-speed mixer (speed range of 5 rev/min to 1000 rev/min for 5 min) before the extrusion process. A twin-screw extruder was used to produce the composites (Rondol Co., Strasbourg, France); the temperatures of the extruder’s barrel were set at 160 °C, 165 °C, 170 °C, and 170 °C for the heating regions of extruder 1, 2, 3, and 4, respectively. The extruded composite pellets were dried at 103 °C to the moisture content of 1% to 2% before the hot press. The pellets were pressed into a board for 10 min at a pressure of 100 bar and a temperature of 180 °C. The specimens obtained from the composite boards were conditioned according to the ASTM D618 (2013) standard.

Fungal decay tests of composites

The malt extract agar was prepared as a culture medium for the cultivation of fungi. The prepared culture mixture was poured into petri dishes and inoculated with the provided fungus mycelium in a laminar flow cabinet. These petri dishes were placed in a culture chamber at 23 °C under 70% relative humidity until fungus mycelium extended the all medium. Then, the papered composite samples were placed into petri dishes with grown fungus mycelium. The durability tests against fungal attack were conducted for 16 weeks and every 4 weeks the mass loss of the samples were recorded. At the end of the cultivation period, the outer mycelia were removed, and the specimens were dried at 103 °C for 24 h and weighed to determine the mass loss caused by the fungi.

The assessment of the durability of the WPCs against fungal attack by basidiomycetes was conducted according to a modified version of European standard EN 113 (1996). The modifications were that the sample dimensions of 25 x 20 x 2 mm and petri dishes were used instead of dimensions of 50 x 25 x 15 mm and Kolle culture flasks recommended in the standard. The evaluation of the laboratory decay test was based on the recorded loss of mass after a fixed time of exposure to the brown-rot fungi, Coniophora puteana (Schum.: Fr., P. Karst), Rhodonia placenta (Fr., Niemelä, K.H. Larss. & Schigel), which were provided by the United States Department of Agriculture, Forest Products Laboratory of Madison Field Office.

The mass loss values were calculated as percentages of the initial total mass. The obtained mass loss was divided by the mass loss of the reference sample (W70), resulting in a ratio referred to as “x value”, as suggested by the European standard EN 350-1. The relative frequency (%) obtained within the specified classes for 8 identical samples for each composite samples after inoculation with rot fungi.

Water absorption capacity tests

The composite samples exposed to the fungus test for 4, 8, 12, and 16 weeks along with control, were firstly dried at 103 °C for 24 h and then immersed in distilled water for 24 h. The control is composite sample not exposed to fungus. A digital balance with the precision of 0.01 g was used to weigh the specimens before and after they were immersed in water. The WAC values were measured and expressed as a percentage for each specimen using Eq. 1,

WA (%) = [(M – M₀) / M₀] ×100 (1)

where M₀ (g) and M (g) are the weights of the composite samples before and after being immersed in distilled water for 24 h, respectively.

Attenuated total reflectance Fourier-transform infrared (ATR-FTIR) spectroscopic analysis of decayed WPCs

Spectroscopic analysis of the samples was performed by using an Agilent Cary 630 model ATR/FTIR equipment (Santa Clara, CA, USA). The spectra of the samples were recorded between 4000 cm^-1and 650 cm^-1 wave frequencies. Baseline and ATR corrections for the penetration depth and frequency variations were applied using the MicroLab software (4.5.93.0, Bozeman, MT, USA) supplied with the equipment.

Thermal analyses

Thermogravimetric analysis (TGA), derivative thermogravimetric analysis (dTGA) and differential thermal analysis (DTA) analyzes were performed using EXSTAR SII TG/DTA 6300 device (Labx, Midland, Canada). The obtained thermal data were interpreted to investigate the effects of biodegradation on the composite structure after fungal decay test comparing the control sample. The analyses of composite samples was performed at heating rate of 10 °C/min and a nitrogen flow rate of 100 mL/min at a temperature range of 25-800 °C. TGA, dTGA, and DTA tests were performed to determine the lignocellulosic mass loss of composite samples exposed to brown rot fungi.

Scanning electron microscopy (SEM) analysis of decayed WPCs

The morphological characteristics of the decayed samples were investigated using SEM, JEOL Neo Scope JSM-500 (JEOL Co., Freising, Germany) under an acceleration voltage of 10 kV. A little piece of the decayed sample was cut, and the surface of this piece was coated with gold (Cressington Scientific Instruments Co., Watford, England) under a vacuum prior to scanning. Then, the effects of the brown rot fungi on the surface of composite samples were recorded.

Statistical analysis

SPSS 20.0 statistical analysis program was used for the fungal decay tests results. The results were subjected to an analysis of variance (ANOVA) at the 95% confidence level, and significant differences between mean values of the samples were determined using Duncan’s multiple range test. The significant differences between the samples were shown with letters, such as A, B, C and D.

RESULTS AND DISCUSSION

Fungal Decay Tests Results

Figure 1 shows the weight losses of the composite samples exposed to R. placenta and C. puteana. The maximum weight loss occurred in the composite that was exposed to R. placenta for 16 weeks. There was a noticeable difference in the weight losses between the composite samples exposed to R. placenta and C. puteana. In addition, zinc borate’s effect on fungal resistance was better in the composite samples exposed to R. placenta. Thus, it was observed that the samples exposed to R. placenta and those exposed to C. puteana decayed at different levels. For example, the weight loss (2.31%) caused by the R. placenta on WPC containing %2 zinc borate were significantly lower than the control sample (12.1%) after 16 weeks. But this value was a little higher (2.84) for C. puteana, while the mass loss of control sample (5.88%) was even lower than half of the control sample of R. placenta for thisfungus. Many studies have shown that brown-rot fungus is more aggressive and lead to more extensive decay in comparison with white-rot fungus on softwoods such as conifers (Fabiyiet al. 2011; Zabel and Morrell 2012).

The results indicated that use of 1% zinc borate increased the decay resistance of the WPCs against the two brown fungi R. placenta and C. puteana. The weight loss of the composite samples loaded with 1% zinc borate was significantly lower than that of the control after 16 weeks. However, it was not enough for entirely protection of composite samples against fungal attack. Especially, the mass losses of both zinc borate containing samples were very close to control samples in first 12 weeks for the C. puteana. However, a considerable difference was visibly ensued after 16 weeks, which was almost half of the mass loss value of control sample W70. The usage zinc borate as biocide in composites containing 70% wood fibers had different effect on the different type of brown rot fungi. Its preservative effect was evidently discerned for the protection of WPCs against fungal decay issued by R. placenta.

On the other hand, when the activities of the two fungus species were compared with each other it was noticed that R. placenta was clearly more effective at decaying of control group. A similar result was reported by Irbe et al. (2006) in their study on chemical composition changes of pinewood (Pinus sylvestris L.) during the fungal decay by brown-rot fungi R. placentaand C. puteana. They found that R. placenta caused more mass loss in wood sample comparing the C. puteana after 4 month of exposure. It was explained that R. placenta tended to degrade cellulose amorphous regions more readily, while C. puteana, possessing full enzyme complement, was able to degrade both amorphous and crystalline regions more readily. Thus, C. puteana caused rapid depolymerization of cellulose chains throughout the cell wall without a considerable loss of cellulose.

Fig. 1. Weight loss of composite samples exposed to R. placenta (a) and C. puteana (b)

Farahani and Banikarim (2013) reported a weight loss of almost 10% for WPCs composed of maple/polyethylene (60/40%) that were treated with nano-zinc oxide at different loadings and exposed to the C. puteana fungus. They also showed that nano-zinc oxide at loadings as high as 3% were enough to prevent the fungal growth on the wood-polypropylene composite. Muller et al. (2013) investigated the fungal resistance of polyvinyl chloride (PVC) and chemically modified wood flour based composites. They found that the moisture contents of the composites were below the limit of fungal activity after inoculation due to some modification. It was reported that some modification process such as aminosilane treatment decreased the weight loss of the composite samples considerably, while the weight loss of the samples treated with acetic anhydride was samples slightly increased compared to the untreated reference. Table 2 shows the statistical analysis results obtained from weight loss data of the composite samples along with relative frequencies of natural durability classes according to the European standard EN350-1.

Table 2. The Homogeneity Groups of Mass Loss Data along with Durability Classes of Samples for Different Fungal Incubation Periods

^aHomogeneity groups; ^bDurability class:Very durable: x≤0.15; Durable: 0.15<x≤ 0.3; Moderately durable: 0.3<x≤0.6; Slightly durable: 0.6<x≤ 0.9; Not durable: 0.9<x. ^cHomogeneity groups with capital letters are given from lowest to highest in the order letter (A-O) and those around it (α<0.05). The capital letters indicate the statistical differences between properties of composite samples by Duncan’ mean separation test.^dRelative frequency.

According to x values of natural durability classes, most of the samples were classified as durable for R. placenta. However, the relative frequencies showed differences due to the changes in the structure of composite samples after exposed to the fungus. Thus, some of the samples classified in different durability classes in the same experiment group of a particular week. Table 2 demonstrated that the addition of zinc borate at a percentage of 1% or 2% into formula was not substantially affect the durability class of the composite sample. This finding was compatible with the results in Fig. 1a and revealed that the zinc borate was demonstrably effective to obtained resistance for this fungus species in WPC with high content of lignocellulosic filler.

On the other hand, the obtained x values for C. puteana showed that most of the samples were classified as not durable. The reason for this situation was attributed to the fact that C. puteana was quite inactive to decay the reference sample W70 in comparison with the R. placenta. Consequently, the samples reinforced with the zinc borate were found as not durable based on the reference samples, even if they had a quite close mass loss to the samples exposed to the R. placenta.

Figure 2 shows the appearances of the composite samples with and without zinc borate during fungal decay tests. The images clearly indicate that both fungi species attacked and completely encased the composite samples in the absence of zinc borate (Figs. 2a and 2c). However, 1% zinc borate effectively prevented fungal decay in the WPCs that had high contents of lignocellulosic filler (Figs. 2b and 2d). The results were clearly compatible with the weight loss values described in the previous section. In addition to the fire-retardant properties of zinc borate, several investigators have reported that the use of zinc borate as an antifungal agent in WPCs can protect the material against fungal decay when the material is under high humidity (i.e., relative humidity of 75 to 85%) in the applications such as outside flooring near seaside and pool sides (Schirp and Wolcott 2005; Klyosov 2007; Kartal et al.2013). In an organic based material, the presence of moisture is an important precondition for biological decay. In WPC, the moisture uptake takes place slowly in the long terms due to hydrophobic plastic. However, the high humidity levels in the outer 5 mm of commercial material can cause fungal attack. Once water has penetrated into the product, it does not easily evaporate owing to the high barrier properties of the plastic, and this paves the way for biological degradation of material (Schirp et al. 2008).

Fig. 2. Appearance of the composite samples after 16 weeks fungal decay tests: a, b) R. placenta; c, d) C. puteana; a, c) sample W70; b, d) sample W70Z1

Water Absorption Capacity Test Results

Table 3 provides the average WAC values for the WPCs that were calculated from the control and the composite samples exposed to fungal decay for 4, 8, 12, and 16 weeks. The maximum WAC occurred in the composite (W70) without zinc borate, which was exposed to R. placenta for 16 weeks.

The WAC values of the composites exposed to fungal decay were very high after 16 weeks when compared to the control samples. The WAC decreased for the composite samples that were loaded with 1% zinc borate. There was not a noticeable difference in the WAC values between the composite samples exposed to R. placenta and C. puteana after 16 weeks. However, Table 2 shows that the addition of zinc borate into composite samples caused a decrease in WAC values. Many studies show that fungal decay is related directly to the absorption of moisture by the composite sample. Moreover, the amount of water absorbed increases as the lignocellulosic content of the composite material increases. Suitable moisture content to start fungal attack is about 20%, however, the ideal value is 30% (Lomeli-Ramirez et al. 2009).

Anti-fungal agents can be used to reduce weight loss in WPCs. However, the wood content of the composite must be taken into account because less wood results in a reduced water uptake and reduced fungal decay. Various studies have shown that the weight losses of WPCs with a mix ratio of 50:50 (wood/plastic) are around 1% (Schirp and Wolcott 2005; Mulleret al. 2013).

During the decay process, the fungal respiration in metabolizing cell wall material of wood can induce the moisture increases as free water available in the wood. These increases can be also promoted via hyphae transport of water. For example, some fungus species can transport water from high humidity environment into drier media such as WPCs to facilitate the fungal decay conditions (Lomeli-Ramirez et al. 2009).

Table 3. The WAC Results of Composites before and after Exposure to Fungal Decay

*Water absorption capacity (%), **Standard deviation

FTIR Spectroscopy Results

The FTIR analysis spectra of the WPCs before the fungal tests and after 16 weeks of fungal degradation for different types of fungi are shown in Figs. 3 and 4. For exact comparison of the chemical changes in the WPCs samples, due to fungal decay, the spectra of W70 and W70Z1 were recorded and given in the figures for each fungus species separately after every month. The analysis of the FTIR spectra of the WPC samples that were exposed to the brown-rot fungi, R. placenta and C. puteana, showed that they generally had a similar level of decay. Although brown-rot fungi do not produce ligninolytic enzymes, they do have a non-enzymatic mechanism that results in the oxidation of the propyl side chains of lignin and oxidative demethylation. According to Goodell (2003), the type and the quantity of lignin have little effect on the decomposition caused by brown-rot fungi.

Brown-rot fungus preferentially attacks C1 through C4 carbohydrates, especially the C1 carbohydrates, which divide the cellulose from the glucomannan skeleton. It is assumed that the fungi cleave the outer ring of the hydroxymethyl (CH₂OH) groups at the parent H-bond binding sites to open up the crystalline structure of cellulose. The amorphous structure of cellulose reduces its ability to repel water and facilitates its enzymatic degradation (Boonstra et al. 2006)

Fig. 3. FTIR spectra of WPCs samples exposed to C. puteana

In the FTIR spectra of all samples, the peaks at 2910 cm^-1 (CH₂ asymmetric stretching), 2843 cm^-1 (CH₂ symmetric stretching), 1460 cm^-1 (CH₂ bending deformation), and 717 cm^-1(CH₂ rocking deformation) remained the same which indicated the presence of polyethylene in the structure of the WPCs. However, increases and decreases were observed in the intensity of the peaks of wood filler due to the species of the fungus in the test and due to the activity of the fungus. When the FTIR spectra of sample W70 was examined, which was exposed to brown-rot fungi, there were noticeable changes in the peaks for the wavenumbers of 895 cm^-1(C-H deformation), 1154 cm^-1 (C-O-C vibrations), and 1365 cm^-1 (C-H deformation) that represented the polysaccharides of cellulose and hemicellulose.

Furthermore, there was a noticeable change in the peak at 1743 cm^-1 (C=O stretching vibration), which represented the xylan’s acetyl groups, which are selectively favored by these fungi. In the samples exposed to the C. puteana fungus, there was no longer a peak at 1743 cm^-1 by the end of the 16 weeks. However, there were substantial increases in the intensities of the peaks at 1595 cm^-1 (C=C aromatic skeletal vibration), 1506 cm^-1 (C=C aromatic skeletal stretching vibration), 1453 cm^-1 (C-H deformation), 1420 cm^-1 (C-H deformation (aromatic ring)), 1260 cm^-1 (C-O stretching), 1211 cm^-1 (C-C, C-O and C=O stretching), 1154 cm^-1 (C-O-C vibrations), and 1021 cm^-1 (C-O stretching), which are the characteristic peaks of lignin. The increase in the density of these peaks occurred at different rates for the two types of fungi (Gulmine et al. 2002; Fabiyi et al. 2011; Kartal et al. 2013; Wei et al.2013).

Fig. 4. FTIR spectra of WPCs samples exposed to R. placenta

When the lignin peaks were compared, the spectra of the R. placenta fungus clearly were more intense than those of the samples exposed to the C. puteana fungus. This indicated that the R. placenta fungus effectively consumed the carbohydrate compounds. Accordingly, the remaining lignin content of the composite samples was more than those of the samples exposed to the C. puteana fungus. After fungal decay, remarkable increases were observed in the intensity of the peaks of absorbed water in the structure in the wave range from 1640 cm^-1to 1650 cm^-1. In addition, the peaks of the syringyl units and C-O primary alcohol in the lignin also increased significantly at the wavenumber of 1313 cm^-1 and 1021 cm^-1, respectively.

When the FTIR spectra of sample W70Z1 were examined, it was clear that 1% zinc borate in the formulation was enough to protect the composite sample. During a 16-week period, no noticeable changes were observed in the chemical structure of the wood filler. While the brown-rot fungi C. puteana and R. placenta effectively decayed the WPCs control samples, they only grew on the nutritional media in the petri dishes and did not attack the composite sample that contained zinc borate. The fact that zinc borate, even in minimal quantities, functioned as an effective antifungal agent in WPCs materials was related to its disruption of the biochemical processes that occurred during the development of the fungi. Boron compounds prevented the development of fungi by causing abnormal growths of hyphae and spores in fungi and by inhibiting the reproduction (Yamaguchi 2003).

Moreover, the metabolic systems of fungal organisms were deteriorated by co-enzymes in the form of oxides as a target of boron ions. In addition, boron ions can penetrate cell walls easily, causing toxic effects and starvation effects in living organisms via the complexes they form (Yamaguchi 2003).

Thermal Analyze Results

When the thermal degradation of wood is examined, it was observed that the active degradation of wood began with the decomposition of cellulose at about 250 °C. The wood structure has different polymeric structures degraded at different points in the TGA curve. The free water molecules in the structure are removed around 100 °C, and decomposition of cellulose and hemicellulose occur in the range 250 to 400 °C. On the other hand, degradation of lignin, a polyphenolic polymer, take place in three stages at three different temperature ranges. These ranges are generally 115 to 225 °C, 225 to 360 °C, and 360 to 500 °C, respectively (Randriamanantena et al. 2009). The thermal degradation of HDPE, a pure polymer, is rapidly observed at a temperature range of 400 to 500 °C as single degradation zone and loses 99% of its mass. The maximum weight loss of HDPE occurs within a temperature range of about 460 to 465 °C (Contat-Rodrigo et al. 2002). In a study, which investigated the thermal properties of wood plastic composites, it was indicated that the all degradation of the composite samples took place in two main zones in TGA curve. The first zone was within the temperature range of 250 °C to 400 °C, and the second zone was between 390 °C and 500 °C. The lignocellulosic material decomposed in the first zone and the plastic polymer decomposed in the second zone (Jeske et al. 2012).

The TGA, dTGA, and DTA curves of sample W70 exposed to R. placenta are given in Fig. 5 for each month. According to dTGA curves, it was clear that the control sample contained more lignocellulosic material than those of other samples exposed to the R. placenta. Because, some of the lignocellulosic material in W70 was consumed by fungus. The peak of lignoselulosic material in the dTGA curve decreased after 16 weeks due to the consuming of lignocellulosics by R. placenta. It is also observed that the active degradation began with the decomposition of cellulose at about 190 °C. It is understood from the dTGA curves that the lignocellulosic materials in W70 degrade between 180 to 400 °C. According to the TGA curve, the maximum degradation temperature of the lignocellulosic material in W70 was around 360 °C and the weight loss was 44.5%. When the DTA curves were examined, the melting peak at 128.3 °C indicated the presence of the HDPE polymer in the composite, while the peak at 351.92 °C was the degradation point of lignocellulose in the composite samples. Finally, the peak at 473.1 °C was the peak of decomposition of the HDPE polymer.

The TGA, dTGA, and DTA curves of sample W70 exposed to C. puteana are shown in Fig. 6. It was observed that the active degradation began with the decomposition of cellulose at about 200 °C. It was understood from the dTGA curves that the lignocellulosic materials in W70 degraded between 200 and 400 °C. According to the TGA curve, the maximum degradation temperature of the lignocellulosic material was at 361 °C and the weight loss was 38.5%. When the DTA curves were examined, the melting peak at 130.3 °C indicated the presence of the HDPE polymer. Morever, the peak at 363.92 °C was the degradation point of lignocellulose in the composite samples, while the peak at 473.98 °C referred deterioration of the HDPE polymer.

Fig. 5. The thermal properties of W70 exposed to R. placenta: a)TGA; b) dTGA; c) DTA.

Fig. 6. The thermal properties of W70 exposed to C. puteana: a) TGA; b) dTGA; c) DTA.

The W70 samples exposed to R. placenta showed higher weight loss than those of exposed to C. puteana according to degradation peak of lignocellulosics in the TGA and dTGA curves. In addition, they had a lower degradation peak according to DTA curve. This was explained due to the fact that the cellulose and hemicelluloses in W70 were consumed more by R. placenta in comparison with C. puteana. This finding supported the weight loss data in Fig. 1. In a different study, pine sapwood was exposed to brown fungus R. placenta and C. puteana for 4, 8, 12 and 16 weeks. The weight loss of the samples exposed to the R. placenta fungus (80.9%) were found to be higher than that of weight loss of the samples exposed to the C. puteana fungus (77.5%) (Irbe et al. 2006).

SEM Analysis Results

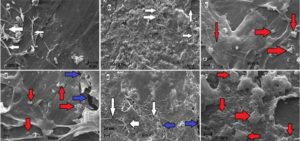
Fig. 7. SEM images of the composite samples (W70) after exposed to R. placenta: fungal mycelium (white arrows); zinc borate (red arrows); surface cracks (blue arrows)

The micrographs of the surface of the decayed composite samples exposed to the fungal attack are given in Fig. 7. These images showed that brown rot fungus attacked the surface of the samples via gaps between matrix and filler of the WPCs (Figs. 7a and 7e). Pendleton et al. (2002) found fungal fragments in the interfacial spaces between the wood and the thermoplastic material in the areas near the surface of the samples exposed to the fungus decay. Furthermore, it was understood that the zinc borate was distributed in the composite structure (Figs. 7c, 7d and 7f). The high amount of plastic matrix was observed on the surface due to decayed filler content (Figs. 7c and 7d). SEM images also demonstrated that fungus mycelium was located on the surface and in some interfacial gaps between the lignocellosic filler and thermoplastic matrix near the sample surface (Figs. 7a, 7b and 7e). Finally, several cavities and cracks were observed on the surface of the samples due to the degradation of filler component by fungal attack (Figs. 7d and 7e).

CONCLUSIONS

Zinc borate increased the resistance of the wood-plastic composites against two different brown rot fungi. When the composite sample with 1% zinc borate was exposed to R. placenta for 16 weeks, the weight loss of the composite was reduced by 10%.
It was apparent that the use of 1% zinc borate prevented the material to a certain extent, but it was not enough to fully prohibit the WPCs samples with 70% wood filler from decay caused by the brown rot fungi.
It was found that the use of 2% zinc borate significantly improved the resistance of WPC to the decay caused by R. placenta and C. puteana fungi in comparison with %1 zinc borate.
The zinc borate effected the WAC properties of the WPCs in a positive way. The WAC of the composite samples containing 1% zinc borate decreased. The highest WAC values were recorded as 27% and 26% for the samples treated by R. placenta and C. puteana.
The FTIR results showed that 1% of zinc borate was enough to hinder the formation of strong chemical variations in the composite samples during fungal attack. During a 16-week period, no noticeable changes were observed in the chemical structure of the wood filler.
TGA results showed that the composite sample exposed to R. placenta showed higher weight loss than the one exposed to C. puteana at the peak point where the lignocellulosics degraded.
The SEM images showed that the brown-rot fungi attacked through the surface cracks and gaps in the wood-plastic composite.

ACKNOWLEDGMENTS

This study was supported by a project (2015/3-44YLS) of the Kahramanmaras Sutcu Imam University in Kahramanmaras, Turkey.

REFERENCES CITED

ASTM D618 (2013). “Standard practice for conditioning plastics for testing,” ASTM International, West Conshohocken, PA, USA.

Boonstra, M. J., Pizzi, A., and Rigolet, S. (2006). “Correlation of 13C‐NMR analysis with fungal decay tests of polymeric structural wood constituents. II. Ground contact tests,” Journal of Applied Polymer Science 102(1), 616-622. DOI: 10.1002/app.24358

Clemons, C. (2002). “Wood-plastic composites in the United States: The interfacing of two industries,” Forest Products Journal 52(6), 10.

Contat-Rodrigo, L., Ribes-Greus, A., and Imrie, C. T. (2002). “Thermal analysis of high-density polyethylene and low-density polyethylene with enhanced biodegradability,” Journal of Applied Polymer Science 86(3), 764-772. DOI:10.1002/app.10974

EN 113 (1996). “Wood preservatives—Test method for determining the protective effectiveness against wood destroying basidiomycetes—Determination of the toxic values,” European Committee for Standardization, Brussels, Belgium.

EN 350-1 (1994). “Durability of wood and wood-based products — natural durability of solid wood — Part 1: Guide to the principles of testing and classification of the natural durability of wood,” European Committee for Standardization, Brussels, Belgium.

Fabiyi, J. S., McDonald, A. G., Morrell, J. J., and Freitag, C. (2011). “Effects of wood species on durability and chemical changes of fungal decayed wood plastic composites,” Composites Part A: Applied Science and Manufacturing 42(5), 501-510. DOI: 10.1016/j.compositesa.2011.01.009

Farahani, M. R. M., and Banikarim, F. (2013). “Effect of nano-zinc oxide on decay resistance of wood-plastic composites,” BioResources 8(4), 5715-5720. DOI: 10.15376/biores.8.4.5715-5720

Goodell, B. (2003). “Brown-rot fungal degradation of wood: Our evolving view,” Wood Deterioration and Preservation 845, 97-118. DOI: 10.1021/bk-2003-0845.ch006

Gulmine, J., Janissek, P., Heise, H., and Akcelrud, L. (2002). “Polyethylene characterization by FTIR,” Polymer Testing 21(5), 557-563. DOI: 10.1016/S0142-9418(01)00124-6

Irbe, I., Andersons, B., Chirkova, J., Kallavus, U., Andersone, I., and Faix, O. (2006). “On the changes of pinewood (Pinus sylvestris L.) chemical composition and ultrastructure during the attack by brown-rot fungi Postia placenta and Coniophora puteana,” International Biodeterioration & Biodegradation 57(2), 99-106. DOI: 10.1016/j.ibiod.2005.12.002

Jeske, H., Schirp, A., and Cornelius, F. (2012). “Development of a thermogravimetric analysis (TGA) method for quantitative analysis of wood flour and polypropylene in wood plastic composites (WPC),” Thermochimica Acta 543, 165-171. DOI:10.1016/j.tca.2012.05.016

Kartal, S. N., Aysal, S., Terzi, E., Yilgor, N., Yoshimura, T., and Tsunoda, K. (2013). “Wood and bamboo-PP composites: Fungal and termite resistance, water absorption, and FT-IR analyses,” BioResources 8(1), 1222-1244. DOI: 10.15376/biores.8.1.1222-1244.

Klyosov, A. A. (2007). Wood-plastic Composites, John Wiley & Sons, New Jersey, USA.

Lomeli-Ramirez, M. G., Ochoa-Ruiz, H. G., Fuentes-Talavera, F. J., Garcia-Enriquez, S., Cerpa-Gallegos, M. A., and Silva-Guzman, J. A. (2009). “Evaluation of accelerated decay of wood-plastic composites by Xylophagus fungi,” International Biodeterioration & Biodegradation 63(8), 1030-1035. DOI: 10.1016/j.ibiod.2009.08.002

Morris, P., and Cooper, P. (1998). “Recycled plastic/wood composite lumber attacked by fungi,” Forest Products Journal 48(1), 86.

Muller, M., Gellerich, A., Militz, H., and Krause, A. (2013). “Resistance of modified polyvinyl chloride/wood flour composites to basidiomycetes,” European Journal of Wood and Wood Products 71(2), 199-204. DOI: 10.1007/s00107-013-0665-8

Naghipour, B. (1997). Effects of Extreme Environmental Conditions and Fungal Exposure on the Properties of Wood-plastic Composites, M.Sc. Thesis, University of Toronto, Toronto, Canada. pp. 3-14.

Ozdemir, F., Ayrilmis, N., Kaymakci, A., and Kwon, J. H. (2014). “Improving dimensional stability of injection molded wood-plastic composites using cold and hot water extraction methods,” Maderas. Ciencia y Tecnologia 16(3), 365-372. DOI: 10.4067/S0718-221×2014005000029

Randriamanantena, T., Razafindramisa, F. L., Ramanantsizehena, G., Bernes, A., and Lacabane, C. (2009). “Thermal behaviour of three woods of Madagascar by thermogravimetric analysis in inert atmosphere,” in: Proceedings of the Fourth High-Energy Physics International Conference, Stanford University, Antananarivo, Madagascar.

Pendleton, D. E., Hoffard, T. A., Adcock, T., Woodward, B., and Wolcott, M. P. (2002). “Durability of an extruded HDPE/wood composite,” Forest Products Journal 52(6), 21.

Schirp, A., and Wolcott, M. P. (2005). “Influence of fungal decay and moisture absorption on mechanical properties of extruded wood-plastic composites,” Wood and Fiber Science37(4), 643-652.

Schirp, A., Ibach, R. E., Pendleton, D. E., and Wolcott, M. P. (2008). “Biological degradation of wood-plastic composites (WPC) and strategies for improving the resistance of WPC against biological decay,” in: Development of Commercial Wood Preservatives: Efficacy, Environmental, and Health Issues, T. P. Schultz et al. (eds.), American Chemical Society, Washington, DC.

Silva, A., Gartner, B. L., and Morrell, J. J. (2007). “Towards the development of accelerated methods for assessing the durability of wood-plastic composites,” Journal of Testing and Evaluation 35(2), 203-210. DOI: 10.1520/Jte100168

Turku, I., Nikolaeva, M., and Karki, T. (2014). “The effect of fire retardants on the flammability, mechanical properties, and wettability of co-extruded PP-based wood-plastic composites,” BioResources 9(1), 1539-1551. DOI: 10.15376/biores.9.1.1539-1551.

Wei, L., McDonald, A. G., Freitag, C., and Morrell, J. J. (2013). “Effects of wood fiber esterification on properties, weatherability and biodurability of wood-plastic composites,” Polymer Degradation and Stability 98(7), 1348-1361. DOI: 10.1016/j.polymdegradstab.2013.03.027

Yamaguchi, H. (2003). “Silicic acid: Boric acid complexes as wood preservatives,” Wood Science and Technology 37(3-4), 287-297. DOI: 10.1007/s00226-003-0190-8

Zabel, R. A., and Morrell, J. J. (2012). Wood Microbiology: Decay and its Prevention, Academic Press, California, USA.

Article submitted: April 10, 2017; Peer review completed: June 29, 2017; Revised version received and accepted: August 7, 2017; Published: August 16, 2017.

DOI: 10.15376/biores.12.4.7161-7177