Effective diameters of drilled holes in pinewood in response to changes in relative humidity

Sydor, M., Majka, J., and Langová, N. (2021). "Effective diameters of drilled holes in pinewood in response to changes in relative humidity," BioResources 16(3), 5407-5421.

Abstract

Wood swelling and shrinkage affect the cooperation among the elements of furniture and should be considered during design. This study investigated the influence of moisture changes to the effective diameter of holes drilled in narrow and in wide sides of pine blanks. The moisture content (MC) of all samples has been averaged to 11.3-11.8% (air-conditioning for 4 month with RH = 60 ± 1% and t = 20 ± 1 °C). The 12 mm holes were drilled in radial and tangential directions of the samples. The MC in half of the samples was increased to 17.4-17.9% (air-conditioning for 6 months with RH = 85% and t = 20 ± 1 °C), and the MC in the second half of the samples was decreased to 8.2% (air-conditioning for six months with RH = 35% and t = 20 ± 1 °C). There were nonuniform changes in MC of the samples. Air with RH = 85% increased the MC by 6%, air with RH = 35% decreased the MC by 3%. The effective diameters of the holes were more sensitive to a decrease in air RH than to an increase the air RH. The swelling changes of wood significantly reduced the effective hole diameter, while adsorption shrinkage changes in wood only slightly increased the effective diameters of the holes. The pine blanks swell and shrink asymmetrically, but the changes in the effective diameter of the holes are not correlated with these phenomena. They also have a different form for holes drilled in radial and tangential directions.

Download PDF

Full Article

Effective Diameters of Drilled Holes in Pinewood in Response to Changes in Relative Humidity

Maciej Sydor,^a,* Jerzy Majka,^b and Nadežda Langová^c

Keywords: Wood moisture; Swelling; Shrinkage; Scots pine; Engineering fit; Sorption hysteresis; Drilled holes, Plug gauge

Contact information: a: Poznań University of Life Sciences, Faculty of Forestry and Wood Technology, Department of Woodworking and Fundamentals of Machine Design, Wojska Polskiego 38/42, 60-637 Poznań, Poland, ORCID 0000-0003-0076-3190; b: Poznań University of Life Sciences, Faculty of Forestry and Wood Technology, Department of Wood Science and Thermal Technics, Poznań, Poland, ORCID 0000-0002-6713-8077; c: Technical University in Zvolen, Faculty of Wood Sciences and Technology, Zvolen, Slovakia, ORCID 0000-0001-5009-9334; *Corresponding author: maciej.sydor@up.poznan.pl

GRAPHICAL ABSTRACT

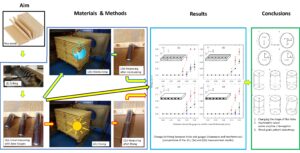
INTRODUCTION

Engineering tolerances determine the size of the clearance or interference between cooperating parts, i.e., it determines the susceptibility of the parts to assembly and subsequent proper functioning of the product. Selecting a designed-in clearance or interference between two parts is an important decision when creating a detailed design. Due to the requirement of full interchangeability of parts, all dimensions should be made with the highest possible accuracy, so that the upper and lower limits of dimension size are close to the nominal size. This increases the susceptibility to assembly and increases the value of products for customers (in Taguchi loss function sense (Deming 1993)). However, the high accuracy complicates the manufacturing of elements and increases the cost of products (Pahl and Beitz 1977).

One of the causes of the dimensional deviations of wood and wood-based materials are processing conditions (e.g., dynamic imbalance of the machine-tool-workpiece system), tool wear, machine setting errors, adverse effect of high temperature on the contact between wood and cutting tool (Kubovský et al. 2020)), conditions of use of the product (e.g., deformation due to long-term loading (creep) (Branowski et al. 2020) or abrasive wear on the surfaces of mating elements), and ambient air conditions (Krišťák et al. 2019).

Wooden elements whose actual dimensions exceed the permissible limits may not be suitable for assembly or may require additional machining, e.g., a hole with too small diameter requires a pin or peg to be pressed into the hole, and a hole with too large diameter may cause the joint to malfunction (Sydor and Wieloch 2009; Branowski et al. 2018; Hitka et al. 2018; Langova et al. 2019).

Wood changes its moisture content (MC) in relation to the changes in ambient air parameters (Machado et al. 2016). Due to the wood-water relations, the effect of even short-term immersion of wood in water or long-term exposure to moist air is swelling (the result of water absorption) or shrinkage (the result of water desorption) of wooden elements (Kollmann and Côté 1968; Noack et al. 1973; Skaar 1988; Wagenführ 2006; Kain et al. 2020). Another undesirable effect of hygroscopic changes in the MC of wood products, apart from the unfavorable effect on the value of clearance and interference of mating parts, may be the risk of cracking (Kulikov 1952, 1968; Kien et al. 1979; Porankiewicz 1989; Kruś 1997; Eckelman 1998; Mirzaei et al. 2015). The change in MC of wood also has a negative effect on the load-bearing capacity of the connections of wood elements in the product (Máchová et al. 2019). The influence of air relative humidity (RH) changes on the dimensions of produced wooden elements was the subject of interest of many researchers (Praast 1982). The conclusions from these studies are implemented in the standard DIN 68100 (2010). This standard describes the principles of tolerance of designed dimensions of wood products including selected species of wood and wood-based materials with equilibrium moisture content (EMC) corresponding to low, intermediate, and high levels of air RH, considering anisotropy of dimensional stability of wood materials (shrinkage and/or swelling). It is worth mentioning that in 2011 the system of Geometrical Product Specification (GPS) standard was introduced (ISO 14638 2015). DIN 68100 is not harmonized with GPS (Riegel 2018).

The sorption phenomenon in wood also depends on wood species, the wood cambial age, and the wood’s chemical composition (Spalt 1958; Wengert 1976; Ahmet et al. 1999; Hernández 2007; Gjerdrum 2008; Feilke et al. 2011; Simón et al. 2015; Majka et al. 2016; Jankowska et al. 2016; Vahtikari et al. 2017; Jankowska 2018). The result of this work was the determination of swelling/shrinkage coefficients. Relationships between air RH and wood MC are approximately proportional, and in the range of MC (ΔN_w) from 0 to 14%, and according to some works up to 20%, they are to some extent reversible and characterized by high anisotropy in relation to the anatomical directions of wood and depending on the species of wood.

Moisture shrinkage or swelling of a wooden product describes the relationship (Kollmann and Côté 1968),

(1)

Where ∆N_w is the change in dimension of a product (mm), β_w is the directional shrinkage/swelling coefficient (radial/tangential/longitudinal in 1/%), ∆MC is the change in moisture content of a product (%), and N is the original dimension of a product (mm).

The use of Eq. 1 to calculate the dimensional changes resulting from sorption has some limitations. First of all, it is used to calculate changes in elements’ dimensions (dimensional addition). Equation 1 does not consider the factor that ultimately determines the “moisture” properties of solid wood furniture elements. The principles of rational wood processing, but also the considerations of ensuring the stability of the shape of wooden parts, are the reason for the common use in the industry of the technology of gluing together of many small wooden elements to obtain members of larger dimensions. As a result, the members have an unambiguous orientation of the wood grains (partly tangential, radial, and semiradial in cross-section) (Langrish and Walker 1993; Pinkowski et al. 2016).

The technical suitability of a batch of sawn timber for the production of wooden elements is determined by not exceeding the permissible MC variation in the batch (Welling 1996). Unfortunately, the inevitable effect of kiln drying is variation in the final moisture content in the kiln batch after drying. This means that the MC of part of the timber batch is usually lower or higher than the permissible value (Keylwerth 1969; Popper et al. 2009; Jankowska 2018). The results of examinations on the MC variation of a Scots pine timber batch during seasoning after drying to MC = 12 ±2% indicate that the effect of constant air parameters is that the timber MC changes unevenly. Part of the timber bath after drying is defective, i.e. it is dry or undried, which is a result of spread in the target (required) moisture content in the batch. After long-term seasoning with constant air conditions (RH = 55%, t = 20 °C) there was still a significant difference between dried and undried MC of timber (Majka et al. 2014).

Increasing the MC of wood (in the hygroscopic range) causes its swelling, while a decrease in the MC causes its shrinking. Most reported swelling / shrinking data correspond to wooden block dimensions, not the dimensions of drilled holes within those blocks. Because wood is not isotropic, there would be a reasonable doubt about whether or not the hole dimensions would follow the dimensional changes. Taking this into account, it has been hypothesized that the changes in MC will cause different results for the effective diameters of holes drilled in pine elements. The novelty of our study is the answer to the questions: What is the effect of changes in the MC of pine wood on the effective diameter of the holes drilled in two different sides of the wood blank? Does the entire structure swell and shrink completely symmetrically?

EXPERIMENTAL

Initial Sample Preparation

Scots pine (Pinus sylvestris L.) wood was selected due to its common industrial use, especially in furniture. Test samples were prepared in two stages using kiln-dried clear sawn timber (target MC = 12 ± 2%). The sample dimensions were 70 mm thickness, 70 mm width, and 400 mm length. Then the blanks were assembled and glued using pieces of blank. The scheme of test samples preparation is shown in Fig. 1. The twin sawn timber were resawn separately in tangential (T) and radial (R) direction (Figs. 1a and 1b, respectively). Finally, two sets of the blanks were assembled and glued into two tangential and radial grain pattern test samples. Four test samples from each tangential and radial blank were resawn (Fig. 1 c, d). The final dimension of the test samples was 18 × 200 × 80 mm (thickness, width and length).

Fig. 1. Scheme of samples preparation: (a, b) cutting, assembling, and gluing pattern of tangential and radial pieces of blank, respectively (1, 2 – tangential and radial grain pattern pieces of blank, respectively; (c, d) top view of assembled to final width tangential and radial blank, respectively and pattern of final cutting and drilling of samples (3, 4 – finished tangential and radial grain pattern blank, respectively; 5, 6 – holes drilling pattern in the narrow and wide side of final twin samples, respectively); the dimension in mm.

Due to possible variations in the MC, all the test samples (2 sets of 4 pieces of radial and tangential grain pattern blank) were subjected to additional long-term air-conditioning under controlled conditions in a container with forced air circulation and seasoned over sodium bromide (NaBr) at air with RH = 60 ± 1% and t = 20 ± 1°C to obtain a constant mass (equilibrium). It was assumed that the applied air parameters correspond to typical conditions of in-door use and averaged the MC of all samples. The duration of this seasoning was 4 months. Table 1 shows the results of MC measurement after the seasoning.

Table 1. Averaged Moisture Content (MC) of Two Sets of Scots Pine Blanks after Air-conditioning

After the air-conditioning was performed, 12 holes with a nominal diameter of 12 mm were drilled in each twin test sample. The hole drilling pattern in the edge and face sides of the test samples are shown in Fig. 1 c. The new, fully sharp twist drill for wood was used (blind bits with a diameter of 12 mm and a length of 77 mm, with carbide blades, manufacturer’s designation HW/D12/NL45/S10x30/GL77/RE – Leitz GmbH & Co. KG, Oberkochen, Germany). A CNC machine tool was used for drilling (Homag Centateq P-110, Schopfloch, Germany). Parameters of drilling used: rotation speed 8000 rpm (cutting speed v_c = 300 m/min), feed 7.2 m/min (chip load f_z = 0.45 mm/tooth).

Seasoning Conditions and Moisture Content Measurements

Before measuring the effective hole diameter all test samples (2 sets of 4 pieces of radial and tangential grain pattern blanks) were subjected to different air conditions. The expected effect of increasing or decreasing the MC of test samples (that have previously been air-conditioned under conditions corresponding to common in-door conditions: RH = 60%, t = 20°C) is the moisture dimensional changes in the wood, respectively swelling and shrinkage, and thus changes in the diameter of the holes drilled in the test samples. It was assumed that under different air conditions of furniture use, air RH may differ from the required one by ± 25%, i.e., corresponding to 85 and 35% (at constant temperature). Therefore, after the holes have been drilled in the sample sides (according to the scheme shown in Fig. 1) all samples were divided into two sets of 4 pieces each, including a grain pattern (tangential, radial) and 12 mm holes were drilled in in narrow and in wide sides of the samples. The separated two sets of samples were again placed in two containers with high (85%) and with low (35%) air RH. The first set of samples was subjected to adsorption with forced air circulation and seasoned to a constant mass with potassium chloride (KCl). Simultaneously, the second set of samples was subjected to desorption to a constant mass with calcium chloride (CaCl₂·6H₂O) (the range of air RH corresponded to typical furniture in-service conditions). The duration of the adsorption and desorption process was 6 months. The MC was measured according to the oven-dry method (EN 13183-1 2002) and calculated by the following formula,

(2)

where m_m was the mass of moist wood and m_o was the oven-dry mass of wood.

The MC values were calculated for each investigated air RH condition (i.e., 35, 60, and 85%) as a mean value of 2 measurements. For measuring the weight of wood samples, an electronic laboratory balance type PA 213/1 was used (OHAUS, Parsippany, NJ, USA) with measurement uncertainty Δm = ± 0.001 g. Results of MC measurements of twin samples after air-conditioning with air conditions corresponding to adsorption and desorption are shown in Table 2. In addition, the range of changes in the MC of the test samples, which was the result of adsorption and desorption, is illustrated in Fig. 2.

Table 2. Increased and Decreased Moisture Content (MC) of Two Sets of Scots Pine Blanks after Air-conditioning

The effect of six months’ exposure of samples to air with RH increased by 25% (from 60 to 85%) was to increase the MC of the test samples by about 6%. At the same time, the effect of exposure to air with RH decreased by 25% (from 60 to 35%) was to halve the change in MC of twin samples, i.e., by 3%. The results of statistical analysis indicate that the average MC values of the two comparative sample sets (containing blanks with tangential and radial grain patterns) achieved during adsorption and desorption did not differ significantly (p < 0.05). The observed disproportion of adsorption and desorption changes in MC of the sets is a result of the sorption hysteresis phenomenon.

Fig. 2. Moisture content changes (ΔMC) of Scots pine twins timber blank according to seasoning conditions: left plot – corresponding to adsorption (increase air RH from 60 to 85%); right plot – corresponding to desorption (decrease air RH from 60 to 35%); gray bar – tangential grain pattern, dark gray – radial grain pattern; the horizontal axis corresponds to the mean MC, which for tangential grain pattern was 11.3%, and for radial grain pattern was 11.8%; error bars represents ± standard deviation; identical superscripts (a, b) denote no significant difference (p < 0.05) between mean values according to post hoc Tukey’s HSD test.

Plug Gauge Fitting Measurements

Scots pine wood has a relatively low hardness (HB 13 to 50 MPa), and its great diversity results from the high cyclical heterogeneity of the structure of early and latewood (Kollmann and Côté 1968; Holmberg 2000; Sydor et al. 2020a). Differences in the hardness of pinewood negatively affect the results of measuring dimensions with typical measuring devices. Even a small measuring pressure on surfaces of small and varying hardness leads to incorrect measurements (Kruś 1997). For this reason, the measurements of the effective diameter of holes were made using a set of 9 plug gauges (single-ended, with diameters ranging from 11.60 mm to 12.00 mm, graded every 0.05 mm). The plug gauges were made of austenitic stainless steel in dimensional tolerance class IT5 (φ12 js5 ± 0.008). The length of the working part of the plug gauge was 33 mm (Fig. 3).

Fig. 3. The plug gauge used in the experiments

The measurements of the holes with plug gauges concerned: (1) samples with averaged MC, (2) samples with increased MC, and (3) samples with decreased MC. To assess the effective diameters, a five-stage dimensionless subjective scale was used (Table 3). The described measurements were performed manually on a workbench. They consisted of placing the plug gauges in holes sequentially, from the plug gauge with the smallest diameter (11.6 mm) to the plug gauge with the largest diameter (12 mm). Final results were calculated as the mean of 12 measurements.

Table 3. Discrete Values and Description of Assumed Joint Fitting Scale

The way that the hole sizes were evaluated does not measure the size of non-circularity. It would be reasonable to employ a caliper gage with a controllable force, as a way to measure two different perpendicular diameters for every hole. This will be done in a future study.

Statistical Analysis

The experimental data were statistically analyzed using STATISTICA 13.3 (TIBCO Software Inc., Palo Alto, CA, USA). Tukey’s post-hoc tests were applied to analyze the significant difference in mean values. The results of verification of hypotheses about the statistical significance of differences in average values of the examined quantities are presented utilizing symbols in the form of lowercase letters of the alphabet (a, b, c… etc.), in case of tabular lists placed behind the values of the quantities. The convention is that identical symbols mean no significant differences between the average values characterizing the examined size. Significance was established at p < 0.05.

RESULTS AND DISCUSSION

The effective hole diameter measurements according to the location of holes in samples and the direction of wood MC changes are illustrated in Fig. 4. Table 4 lists the effective hole diameters for all variants of the test samples.

Table 4. Effective Diameters of the Holes (in mm) Taking into Account: Moisture Content, Grain and Hole Drilling Patterns in Scots Pine Timber Blank

Fig. 4. Fitting the plug gauge for holes according to grain pattern (a, c – tangential, b, d – radial), holes drilling (a, b – in the wide side of the sample, c, d – in the narrow side of the sample), and moisture content (black lines – RH = 60%; blue lines – corresponding to adsorption (increased RH from 60 to 85%); red lines – corresponding to desorption (decreased RH from 60 to 35%); dots represents mean values (n = 12), error bars depicted ± standard deviation; limit values of fitting scale: 0 – loose running (larger clearance, can be assembled), 1 – interference fits (press fits, cannot be assembled).

A general observation is that regardless of the location of the holes (wide side or narrow side of the test sample) and regardless of the grain pattern (tangential or radial):

For the samples with average MC (airconditioned with RH = 60%): plug gauges with diameters up to 11.85 mm can be inserted into the holes without any resistance, plug gauges with diameters from 11.90 to 12.0 mm are insertable, but with increased resistance.

For the samples with increased MC (airconditioned with RH = 85%): plug gauges can be inserted into the holes over the entire range of tested diameters (11.60 to 12.0 mm); only in the case shown in Fig. 4a, was there a slight resistance with diameters of 11.95 and 12.0 mm.

For the samples with decreased MC (airconditioned with RH = 35%): the effective diameter of the holes decreased noticeably. In the case of 4a, this reduction was 0.1 mm; in other cases, 0.05 mm; in the case shown in Fig. 4a, it was not possible to insert plug gauges with diameters of 11.95 and 12.00 mm in the holes.

The results of the experiments, as presented in Fig. 4 and Table 4, show that increasing MC did not reduce the effective hole diameters, but even increased them. On the other hand, decreasing MC significantly reduced the effective hole diameters.

The results of this research confirm the results of many authors that the range of changes in both MC and dimensions of wood elements depends on the sorption phenomena, i.e., adsorption and desorption (Keylwerth 1969; Popper et al. 2009; Jankowska 2018). The change in wood MC translates into changes in the dimensional tolerance of individual elements and, consequently, changes in the types of fits of pairs of elements. Porankiewicz (1989) stated that achieving MC equilibrium by a batch of elements with different initial MC results in different dimensions of holes made in particular elements of the batch (increasing the field of manufacturing tolerance). On the other hand, a change in the MC of a batch of elements with similar MC before seasoning does not affect the dimensional tolerance of individual elements, but it usually affects the fit for pairs of elements (affects the value of play and pin-hole pair pressure). Kulikov (Kulikov 1968) analyzed differences in MC on the cross-sections of the batch of elements made of previously kiln-dried sawn timber to associate the elements in a way that allows for subsequent limitation of unfavorable joint loosening. The basic difficulty is that in solid wood products the basic anatomical direction is rarely aligned exactly. The orientation of annual growths on the cross-sectional area of sawn timber elements (tangential materials, radial materials) is random and is determined by the previously applied mechanical wood processing technology (Langrish and Walker 1993).

The explanation for the results of the research is that moisture deformations of wood occur in different anatomical directions with different intensities. Anatomical directions in the wood are shown in Fig. 5.

Fig. 5. Diagram illustrating the radial (R), tangential (T), and longitudinal (L) directions both in a log and in a board cut from it (based on Eckelman 1998 p. 7).

The shrinkage in tangential (T) direction is two times greater than in the radial direction∙(R) and the shrinkage in the longitudinal (L) direction is negligible L << T (L/T ≈ 0.05) (DIN 68100 2010). The relationships between these deformations can be written: T ≈ 2R ≈ 16 L. The results of the tests may be explained by the fact that the cross-sections of the holes were deformed (they obtained shapes similar to an ellipse) due to the anisotropy of contraction in directions perpendicular to the grain, i.e., radial (R) and tangential (T). Figure 6 illustrates the options of translational deformation of the cross-section of the hole (markings a-d in Fig. 6 are compatible with markings a-d in Fig. 4).

Fig. 6. Observed round hole cross-sectional deformations: a – holes drilled along the R direction, in the wide surface of the sample (L-T plane), b – holes drilled along the T direction, in the wide surface of the sample (L-R plane), c – holes drilled along the L direction, in the narrow surface of the sample (R is the sample thickness) (R-T plane), d – holes drilled along the L direction, in the narrow surface of the sample (T is the sample thickness) (R-T plane).

Characteristic for the research is the case “a” (Fig. 4a), in which reducing the moisture content (MC) of the samples to the greatest extent reduced the effective hole diameter. In this case, it seems that the key role was played by the substantial difference of the wood shrinkage in the L and T directions. It caused a significant ovalization of the hole (as shown in Fig. 6a). This form of deformation is confirmed by Eckelman’s observations from 1998 (Eckelman 1998 p. 7).

Deformations can also occur “in volume”. Examples of cylindrical deformations of holes are shown in Fig. 7.

Used in our study the hole measurement methodology has some limitations. Only the smallest diameter of the ellipse resulting from the change in MC can be obtained (therefore, it was only possible to measure the effect in one anatomical direction). Furthermore, the scale used to place the value of the joint fitting scale is subjective (Table 3). However, even such a subjective scale indicates the character of changes in the dimensions of the openings due to changes in MC. Using metal plug gauges can also deform the wood. The advantage of the measurement method used is that it has no impact on the hole diameters. Large contact area between the gauge and hole and performing the tests by hand, not by machine, does not affect the smoothing of the surfaces roughness of the wood in holes. In the authors’ opinion, using simple or specialized calipers for small hole diameters would have a negative effect on the accuracy of measurements (Kruś 1997), but it would allow to measure in three anatomical directions (L, R, T, two for every hole). A promising method for analysing the holes parameters is the optical method. The optical measurement method was used to determine the accuracy of the location of the holes (Sydor et al. 2020b), but there were great difficulties in correctly determining the edge of the measured hole, which is a typical problem in the case of scanning wood materials.

No results were found in the literature on the influence of sorption hysteresis on the form of deformed holes. This may be the subject of further research.

Fig. 7. Examples of cylindricity deformations: a – nominal cylinder, b – conicity deviation, c – barrel-like deviation, d – saddle like deviation, e – median line deviation, f – complex deviation.

CONCLUSIONS

The increase in the moisture content (MC) of Scots pine blank, caused by an increase in the air relative humidity (RH) by 25%, is two times higher than the opposite change in MC, caused by a decrease in air RH by 25%.
The decrease in the MC of the samples reduces the effective diameter of the holes drilled in the narrow sides of the blanks.
Increasing the MC of the samples has a limited impact on the change in the effective diameter of the holes drilled in the narrow sides of the blanks.
Changes in the engineering fit of pine wood elements due to an increase in its MC are not symmetrical to the changes due to a decrease in its MC. This is due to the sorption hysteresis phenomenon.
The decrease in the holes effective diameter, when increasing MC, is due to the different directional shrinkage of the wood (which changes the cross-section of the holes from round to oval). The most oval are the holes drilled along the R wood direction (perpendicular to the L-T plane of the wood) because the difference in the wood shrinkage in the L and T directions is the greatest.
The location of grain pattern to the hole position greatly influences the moisture changeability of the cooperation nature in wooden components. Grain pattern is critical in designing an engineering fit in wooden structures for assembly in variable ambient air conditions.

ACKNOWLEDGMENTS

The authors thank Jacek Sydor for insightful comments on the manuscript. This research was funded by the Slovak grant agency VEGA, grant number 1/0556/19 Lightweight wood veneers-based materials and their application in products. The APC was funded by Slovak grant agency VEGA.

Author Contributions: Conceptualization, M.S. and J.M.; methodology, J.M. and M.S.; validation, M.S., J.M. and N.L.; formal analysis, J.M.; investigation, J.M.; resources, M.S. and J.M.; data curation, M.S.; writing—original draft preparation, M.S. and J.M.; writing—review and editing, M.S.; visualization, J.M.; supervision, M.S.; project administration, N.L.; funding acquisition, N.L. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement: All data, models, and code generated or used during the study appear in the submitted article.

Conflicts of Interest: The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

REFERENCES CITED

Ahmet, K., Dai, G., Jazayeri, S., and Tomlin, R. (1999). “Experimental procedures for determining the equilibrium moisture content of twenty timber species,” Forest Products Journal 49(1), 88-93.

Branowski, B., Starczewski, K., Zabłocki, M., and Sydor, M. (2020). “Design issues of innovative furniture fasteners for wood-based boards,” BioResources 15(4), 8472-8495. DOI: 10.15376/biores.15.4.8472-8495

Branowski, B., Zabłocki, M., and Sydor, M. (2018). “Experimental analysis of new furniture joints,” BioResources 13(1), 370-382. DOI: 10.15376/biores.13.1.370-382

Deming, W. E. (1993). The New Economics for Industry, Government, Education, Massachusetts Institute of Technology, Cambridge, MA.

DIN 68100 (2010). “Toleranzsystem für Holzbe- und -verarbeitung – Begriffe, Toleranzreihen, Schwind- und Quellmaße / Tolerance system for wood working and wood processing – Concepts, series of tolerances, shrinkage and swelling,” Deutsche Institut für Normung, Berlin, Germany.

Eckelman, C. A. (1998). The Shrinking and Swelling of Wood and its Effect on Furniture, Report FNR 163, Department of Forestry &Natural Resources, Purdue University, West Lafayette, IN, USA.

EN 13183-1. (2002). “Moisture content of a piece of sawn timber. Part 1: Determination by oven dry method,” European Committee for Standardization, Brussels, Belgium.

Feilke, T., Zimmer, K., Fromm, J., and Larnøy, E. (2011). “Sorption behaviour of Scots pine in Northern Europe,” in: Proceedings of the 7th meeting of the Nordic-Baltic Network in Wood Material Science and Engineering (WSE), Oslo, Norway, pp. 131-136.

Gjerdrum, P. (2008). “Modeling moisture sorption and its dynamics in commercial, kiln-dried softwood boards,” Drying Technology 26(9), 1140-1144. DOI: 10.1080/07373930802266215

Hernández, R. E. (2007). “Moisture sorption properties of hardwoods as affected by their extraneous substances, wood density, and interlocked grain,” Wood and Fiber Science, 39(1), 132-145.

Hitka, M., Joščák, P., Langová, N., Krišťák, L., and Blašková, S. (2018). “Load-carrying capacity and the size of chair joints determined for users with a higher body weight,” BioResources 13(3), 6428-6443. DOI: 10.15376/biores.13.3.6428-6443

Holmberg, H. (2000). “Influence of grain angle on Brinell hardness of Scots pine (Pinus sylvestris L.),” Holz als Roh- und Werkstoff, 58(1), 91-95. DOI: 10.1007/s001070050392

ISO 14638. (2015). “Geometrical product specifications (GPS) — Matrix model,” International Organization for Standardization.

Jankowska, A. (2018). “Assessment of sorptive properties of selected tropical wood species,” Drvna Industrija 69(1), 35-42. DOI: 10.5552/drind.2018.1733

Jankowska, A., Drożdżek, M., Sarnowski, P., and Horodeński, J. (2016). “Effect of extractives on the equilibrium moisture content and shrinkage of selected tropical wood species,” BioResources, 12(1), 597-607. DOI: 10.15376/biores.12.1.597-607

Kain, G., Idam, F., Federspiel, F., Réh, R., and Krišťák, Ľ. (2020). “Suitability of wooden shingles for ventilated roofs: An evaluation of ventilation efficiency,” Applied Sciences 10(18), 6499. DOI: 10.3390/app10186499

Keylwerth, R. (1969). “Praktische Untersuchungen zum Holzfeuchtigkeits-Gleichgewicht,” Holz als Roh- und Werkstoff 27(8), 285-290. DOI: 10.1007/BF02612702

Kien, W., Kortylewski, B., Miński, K., Palka, Z., Porankiewicz, B., Staniszewska, A., Staniszewski, J., and Szymański, W. (1979). Tolerancje i pasowania wymiarów liniowych drewna w przemyśle meblarskim / Geometric dimensioning and tolerancing of linear dimensions of wood in the furniture industry, Report, Instytut Podstaw Techniki, Wyższa Szkoła Rolnicza / Institute of Fundamentals of Technology, University of Agriculture, Poznań, Poland.

Kollmann, F. F., and Côté, W. A. (1968). Principles of Wood Science and Technology. I Solid Wood, Springer-Verlag, Berlin-Heidelberg.

Krišťák, Ľ., Igaz, R., and Ružiak, I. (2019). “Applying the EDPS method to the research into thermophysical properties of solid wood of coniferous trees,” Advances in Materials Science and Engineering 2019, 1-9. DOI: 10.1155/2019/2303720

Kruś, S. (1997). “Metrologia techniczna a specyfika drewna na przykładzie układu tolerancji i pasowań / Metrology and technical specificity of wood on the example system of geometric dimensioning and tolerancing,” Zeszyty Naukowe Wyższej Szkoły Pedagogicznej w Bydgoszczy. Studia Techniczne (19), 193-202.

Kubovský, I., Krišťák, Ľ., Suja, J., Gajtanska, M., Igaz, R., Ružiak, I., and Réh, R. (2020). “Optimization of parameters for the cutting of wood-based materials by a CO₂ laser,” Applied Sciences 10(22), 8113. DOI: 10.3390/app10228113

Kulikov, I. V. (1952). Допуски и Предельные Калибры в Деревообработке / Limits and Fits in Woodworking, book, Гослесбумиздат / [Publishing house] Goslesbumizdat, Leningrad, USSR.

Kulikov, I. V. (1968). Новое в Технологии Сборки Изделий из Древесины / New technology in the assembly of wood products, Лесна́я промы́шленность / [Publishing house] Wood industry, Moskva, USSR.

Langova, N., Réh, R., Igaz, R., Krišťák, Ľ., Hitka, M., and Joščák, P. (2019). “Construction of wood-based lamella for increased load on seating furniture,” Forests 10(525). DOI: 10.3390/f10060525

Langrish, T. A. G., and Walker, J. C. F. (1993). “Transport processes in wood,” in: Primary Wood Processing: Principles and Practice, J. C. F. Walker, B. G. Butterfield, J. M. Harris, T. A. G. Langrish, and J. M. Uprichard (eds.), Springer Netherlands, Dordrecht, pp. 121-152. DOI: 10.1007/978-94-015-8110-3_5

Machado, J. S., Santos, S., Pinho, F. F. S., Luís, F., Alves, A., Simões, R., and Rodrigues, J. C. (2016). “Impact of high moisture conditions on the serviceability performance of wood plastic composite decks,” Materials & Design 103, 122-131. DOI: 10.1016/j.matdes.2016.04.030

Máchová, E., Langová, N., Réh, R., Joščák, P., Krišťák, Ľ., Holouš, Z., Igaz, R., and Hitka, M. (2019). “Effect of moisture content on the load carrying capacity and stiffness of corner wood-based and plastic joints,” BioResources 14(4), 8640-8655. DOI: 10.15376/biores.14.4.8640-8655

Majka, J., Czajkowski, Ł., and Olek, W. (2016). “Effects of cyclic changes in relative humidity on the sorption hysteresis of thermally modified spruce wood,” BioResources 11(2), 5265-5275. DOI: 10.15376/biores.11.2.5265-5275

Majka, J., Olek, W., and Kudła-Chwiłowicz, Z. (2014). “Determination of moisture content changes in kiln-dried Scots pine timber during storage,” Drewno. Prace naukowe. Doniesienia. Komunikaty (191), 45-54. DOI: 10.12841/wood.1644-3985.052.03

Mirzaei, B., Sinha, A., and Nairn, J. A. (2015). “Using crack propagation fracture toughness to characterize the durability of wood and wood composites,” Materials & Design 87, 586-592. DOI: 10.1016/j.matdes.2015.08.010

Noack, D., Schwab, E., and Bartz, A. (1973). “Characteristics for a judgment of the sorption and swelling behavior of wood,” Wood Science and Technology 7(3), 218-236. DOI: 10.1007/BF00355552

Pahl, G., and Beitz, W. (1977). Konstruktionslehre: Handbuch für Studium und Praxis, Springer Verlag, Berlin.

Pinkowski, G., Krauss, A., and Sydor, M. (2016). “The effect of spiral grain on energy requirement of plane milling of Scots pine (Pinus sylvestris L.) Wood,” BioResources 11(4), 9302-9310. DOI: 10.15376/biores.11.4.9302-9310

Popper, R., Niemz, P., and Croptier, S. (2009). “Adsorption and desorption measurements on selected exotic wood species: Analysis with the Hailwood-Horrobin model to describe the sorption hysteresis,” Wood Research 54(4), 43-56. DOI: 10.3929/ethz-a-006104740

Porankiewicz, B. (1989). Problemy Układu Tolerancji i Pasowań dla Przemysłu Drzewnego / Issues of geometric dimensioning and tolerancing for wood industry, book, Wydawnictwo Akademii Rolniczej im. A. Cieszkowskiego w Poznaniu / Publishing House of the The August Cieszkowski Agricultural University of Poznań, Poznań, Poland.

Praast, S. (1982). “Einheitliches Toleranzsystem für die Längenmaße bei Holz und Holzwerkstoffen,” Holz als Roh – und Werkstoff 40(3), 101-104. DOI: 10.1007/BF02612569

Riegel, A. (2018). “Geometric tolerancing of furniture,” in: Proceedings 8^th International Conference “Production Engineering and Management, F. J. Villmer and E. Padoano (eds.), Hochschule Ostwestfalen-Lippe, University of Applied Sciences, Lemgo, Germany, pp. 161-171.

Simón, C., Esteban, L. G., de Palacios, P., Fernández, F. G., Martín-Sampedro, R., and Eugenio, M. E. (2015). “Thermodynamic analysis of water vapour sorption behaviour of juvenile and mature wood of Abies alba Mill.,” Journal of Materials Science 50(22), 7282-7292. DOI: 10.1007/s10853-015-9283-7

Skaar, C. (1988). Wood-water Relations, Springer-Verlag, Berlin; New York.

Spalt, H. (1958). “Water vapor sorption by wood,” Forest Product Journal 8, 288-295.

Sydor, M., Pinkowski, G., and Jasińska, A. (2020a). “The Brinell method for determining hardness of wood flooring materials,” Forests 11(8), 878. DOI: 10.3390/f11080878

Sydor, M., Rogoziński, T., Stuper-Szablewska, K., and Starczewski, K. (2020b). “The accuracy of holes drilled in the side surface of plywood,” BioResources 15(1), 117-129. DOI: 10.15376/biores.15.1.117-129

Sydor, M., and Wieloch, G. (2009). “Construction properties of wood taken into consideration in engineering practice,” Drewno. Prace naukowe. Doniesienia. Komunikaty 52(181), 63-73.

Vahtikari, K., Rautkari, L., Noponen, T., Lillqvist, K., and Hughes, M. (2017). “The influence of extractives on the sorption characteristics of Scots pine (Pinus sylvestris L.),” Journal of Materials Science 52(18), 10840-10852. DOI: 10.1007/s10853-017-1278-0

Wagenführ, R. (2006). Holzatlas, Fachbuchverlag Leipzig im Carl Hanser Verlag, München.

Welling, J. (1996). “Zur Ermittlung der Trocknungsqualität von Schnittholz / Assessment of drying quality of sawn timber,” Holz als Roh – und Werkstoff 54(5), 307-311. DOI: 10.1007/s001070050191

Wengert, E. M. (1976). “Predicting average moisture content of wood in a changing environment,” Wood and Fiber Science 7(4), 264-273.

Article submitted: May 14, 2021; Peer review completed: June 7, 2021; Revised version received and accepted: June 8, 2021; Published: June 10, 2021.

DOI: 10.15376/biores.16.3.5407-5421