Effects of selected factors on spruce dowel joint stiffness

Abstract

Joints are used to join furniture parts, and they represent a critical part of the structure of furniture. The quality of joints is greatly affected by the accuracy of their execution. When designing furniture, it is important to carefully consider the type of joint used so that it can hold all the joined elements together. Under loading of the joined structures, internal forces develop, which can lead to failure of the joints. This study investigated the elastic stiffness of spruce (Picea abies L.) dowel joints. The effects of selected factors such as the type of loading (compressive versus tensile), the size of the dowels (one-half versus one-third of the thickness of the joined elements), the type of adhesive used (polyvinyl acetate versus polyurethane), and annual ring deflection were examined. Spruce dowel joints exhibited the highest elastic stiffness values with a higher-diameter dowel glued with PUR adhesives and subjected to compressive loading. The impact of annual rings was not a significant factor. Finally, the reference type joints were compared with other commonly used types, such as three types of mortise and tenon joints (simple, haunched, and dovetail).

Full Article

Effects of Selected Factors on Spruce Dowel Joint Stiffness

Vladimír Záborský, Gourav Kamboj, Adam Sikora,* and Vlastimil Borůvka

Joints are used to join furniture parts, and they represent a critical part of the structure of furniture. The quality of joints is greatly affected by the accuracy of their execution. When designing furniture, it is important to carefully consider the type of joint used so that it can hold all the joined elements together. Under loading of the joined structures, internal forces develop, which can lead to failure of the joints. This study investigated the elastic stiffness of spruce (Picea abies L.) dowel joints. The effects of selected factors such as the type of loading (compressive versus tensile), the size of the dowels (one-half versus one-third of the thickness of the joined elements), the type of adhesive used (polyvinyl acetate versus polyurethane), and annual ring deflection were examined. Spruce dowel joints exhibited the highest elastic stiffness values with a higher-diameter dowel glued with PUR adhesives and subjected to compressive loading. The impact of annual rings was not a significant factor. Finally, the reference type joints were compared with other commonly used types, such as three types of mortise and tenon joints (simple, haunched, and dovetail).

Keywords: Furniture joints; Spruce dowel joints; Elastic stiffness

*Corresponding author: sikoraa@fld.czu.cz

INTRODUCTION

The joints are the most important parts of wooden structures. These elements significantly affect the overall behavior of the structure of the joined components. Joints provide continuity to the member and strength and stability to the structure. Proper joint design is important so that joints can carry a load safely in service conditions without excessive deformation or failure (Eckelman et al. 2003). The mechanical strength of a piece of furniture depends mostly on the strength of its joints. One of the main advantages of using wood as a structural material is that each structural element can easily be connected with a wide range of fasteners, and the joints may entirely consist of wooden members (Gaff and Babiak 2017).

The dowel joint is used often in the furniture industry. In this type of joint, a short wooden rod is inserted into a wooden drill hole for the proper connection. In historical timber structures, traditional carpentry joints were used, while wooden dowels fixed the mutual position of the elements. Dowels are often used as primary connectors in furniture frames constructed of both solid wood and wood-based composites (Fukuyama et al. 2007). However, because wood is hygroscopic, it is common to see the wood dowel become unfastened in the furniture joint. Drilling dowels uses less energy than milling. Less waste is created, simplifying the production process and making it faster, as the necessary profile and holes for the dowels are formed by one machine. This increases manufacturing productivity and reduces production costs.

The dowel joints have some advantageous aspects that may compensate for their lower strength. Due to their profile and hole formed by one machine, their production is fast and simple, which increases productivity and reduces production costs. (Efe et al. 2005; Hrovatin et al. 2013; İmirzi et al. 2015). The strength of these joints is somewhat limited relative to the strength of the joint member, so unless they are properly designed, they may be the weakest part of the furniture frame. In a furniture frame, dowel joints may be subjected to axial, shear, tensional, and bending forces (Pizzi et al. 2004). The knowledge of the mechanical behavior of these dowel-type connections (the loading distribution, ultimate strength, and failure modes) is important for their intelligent application. The complex behavior is governed by several geometric, material, and load parameters (e.g., wood species, dowel diameter, end and edge distance, space between connectors, clearance, friction, and load configuration) (Vaziri et al. 2010). Some techniques have been developed to assess the relationship between the parameters and the mechanical behavior of the connectors and joints in different timber structures (Albin 1989; Eckelman 1989; Eckelmann and Rabiej 1985; Loferski and Gamalath 1989; Ozcifci 1995; Kanazawa et al. 2005; Martins et al. 2013). Generally, the size of the bending moment and the stiffness of the dowel joints is affected by the dowel spacing, diameter, and the depth of the dowel (Warmbier and Wilczynski 2000). Zhang (1991) stated that the optimal diameter was 8 mm, the optimal depth of dowel embedment in a face member was 16 mm, and the optimal depth of dowel embedment in the edge member of the corner joints was 25.4 mm. Joint stiffness increases when a greater number of dowels is used. Adhesive bonding technology has played an essential role in the development and growth of conservation and the repair of timber structures (Gaff et al. 2016). Better joint stiffness is achieved with a thicker joint, but this property is influenced by other factors, particularly the type of adhesive used. Tankut (2007) emphasized the importance of the choosing the right type of adhesive.

The aim of this study was to determine the elastic stiffness of spruce dowel joints under the influence of the selected factors of dowel size (diameters of 8 mm and 12 mm), adhesive used (PVAc and PUR), type of loading (tensile and compressive force in angular plane), and annual ring deflection. The use of the joints was compared with that of the traditional constructional joint.

EXPERIMENTAL

Materials

Spruce wood (Picea abies L.) was used in the experiment to make the corner dowel joint (Polana, Slovakia). A diagram of the tested joints is shown in Fig. 1. The cutting was performed at a moisture content of 10%, relative humidity of 55%, and a temperature of 20 °C. According to EN 942 (2007), ČSN 91 0001 (2007), and ČSN 91 0000 (2005), the moisture content corresponds to the equilibrium moisture content of the furniture components intended for indoor environments. The specimens for mechanical testing were made from dried lumber using woodworking machines at a vocational school in Spišská Nová Ves (Slovakia). To connect the joint elements, spruce dowels with a diameter of 8 mm and 12 mm and a length of 50 mm were used.

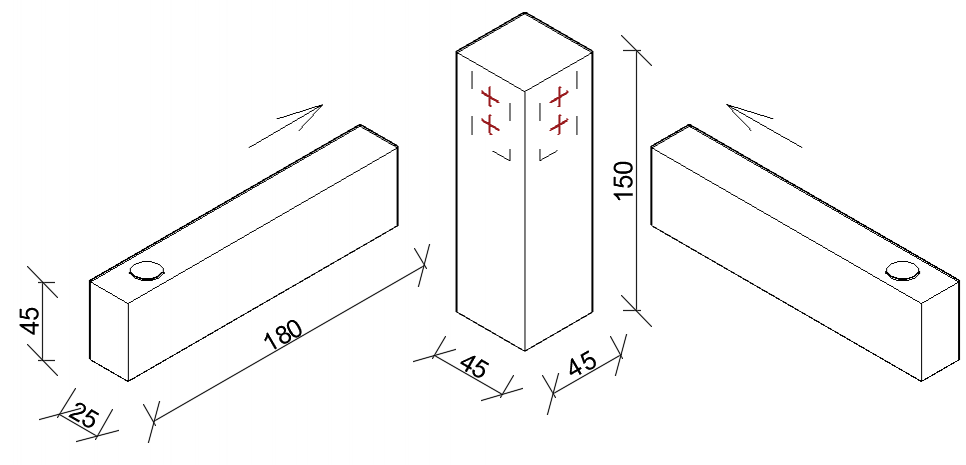
Fig. 1. Structure and dimension of the tested dowel joint

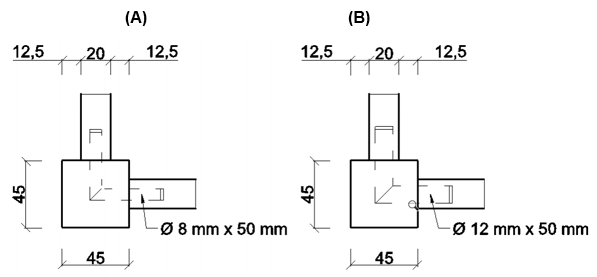
Fig. 2. Geometries of (A) dowel with 8 mm diameter; (B) dowel with 12 mm diameter

Using 8 mm and 12 mm drill bits, holes were drilled according to the dowel sizes and rails. Joints with 8 mm dowels corresponded to a joint thickness that was 1/3 the thickness of the rail, and 12 mm dowels corresponded with a joint 1/2 the thickness of the rail. The location of the dowels and their dimensions are shown in Fig. 2.

Two types of adhesives were used in the joining elements: a single-component, waterproof polyvinyl acetate adhesive (PVAc) AG-COLL (EOC, Oudenaarde, Belgium) 8761/L D3 (EOC, Oudenaarde, Belgium) and a single-component polyurethane adhesive (PUR) NEOPUR 2238R (NEOFLEX, Madrid, Spain). Detailed parameters of these adhesives are shown in Table 1. The adhesives were applied manually to the holes in a single-sided coating of 150 g/m2 to 180 g/m2 for PVAc, and 180 g/m2 to 250 g/m2 for the PUR adhesive. The test specimens were cold-pressed in manual clamps. After the pressing, the samples were conditioned in a climatic chamber at 20 °C and at a relative humidity of 55%.

Table 1. Parameters of the PVAc and PUR Adhesives

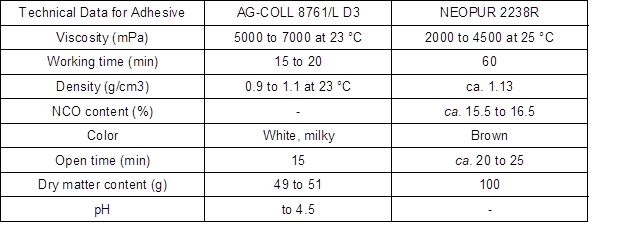
The effects of the annual rings with angles of 45°, 45° to 90°, and 90° were investigated, as shown in Fig. 3. The effect of annual ring deflection was evaluated separately from other monitored factors.

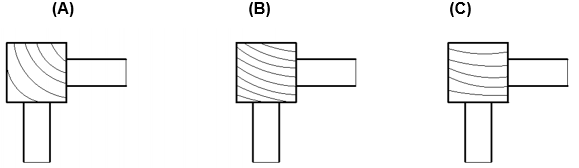
Fig. 3. Schematic of annual ring deflection: (A) 45°; (B) 45 to 90°; (C) 90° (Záborský et al. 2018)

A total of 80 joint specimens representing two types of dowel joints were constructed of spruce wood (Picea abies L.). The monitored factors affected the elastic stiffness of joints were joint thickness (1/2 and 1/3), type of loading (compressive and tension) and type of adhesive (PUR and PVAc). For each monitored factor, 10 samples were created in each test group. Figure 4 shows the classification of the tested joints.

Methods

All joint samples were conditioned and kept at approximately 12% moisture content before and during the testing time. These calculations were performed according to ISO 13061-1 (2014). The density of the specimens was evaluated per the ISO 13061-2 (2014) standard. The specimens were obtained in oven-dry state according to ISO 13061-1 (2014).

A universal testing machine TIRA 50 (TIRA System GmbH, Schalkau, Germany) for compressive and tensile loads was used to measure the elastic stiffness of the corner joint. This study used the same type of steel clamp that was used in the work of Podlena and Borůvka (2016). Figure 5b shows the experimental testing of the corner joint and its mounting on the device. Figure 5a shows that the testing samples were loaded by the bending moment with the tensile and compressive forces applied in an angular plane.

Fig. 4. Classification of the tested half and one third thickness joints

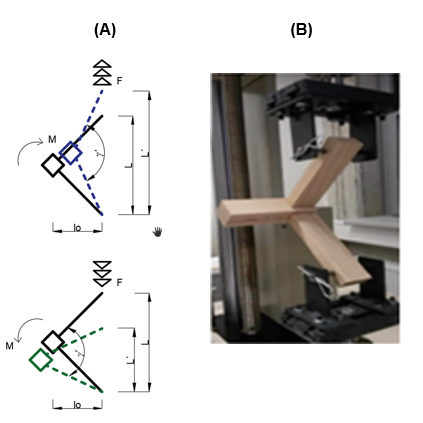
Fig. 5. (A) Diagram showing the bending moment of tension a compressive load; (B) test sample attached to the test device

The change in the distance between the dowels of the device was recorded (L → L´) and used to calculate the angle arc-sin function γ´ (Záborský et al. 2018, Warmbier and Wilczynski 2000). Equation 1 was used to calculate the angular displacement ∆γ.

Table 2. Basic Statistical Analysis of Density and Elastic Stiffness of Wood Joints

Equation 2 was used to calculate the change in torque ∆M,

∆M = ∆F × l0 (2)

where Δ F represents the difference between the two forces (N) that was recorded in the stress-strain diagrams at 10% to 40% of the maximum joint strength, and l0 represents the vertical arm (mm) of the tested joint in the direction of loading force.

The elastic stiffness, celast (Nm/rad), was calculated according to Eq. 3 as the ratio of the change in torque to the angular displacement in radians.

RESULTS AND DISCUSSION

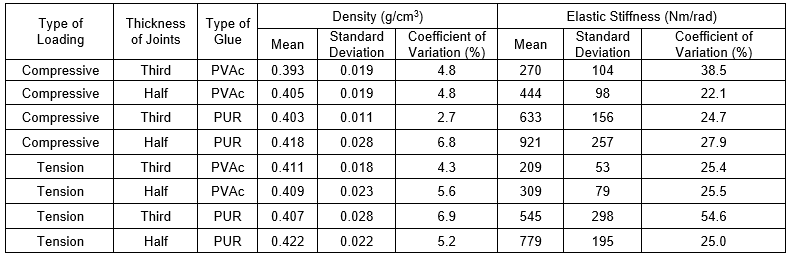
Table 2 shows a statistical analysis of the density and elastic stiffness of spruce wood joints. For spruce specimens, the average density was 0.408 g/cm3, and the average elastic stiffness was 514 Nm/rad, which is lower than that of the beech dowel joint at 940 Nm/rad (Záborský et al. 2018). A relatively large variation coefficient, as was observed, that can be explained by undetected defects in the wood structure. The maximum elastic stiffness was reached in samples with a half-thickness joint bonded with PUR adhesive under compressive loading (Table 2), which is nearly the same result as that obtained by Jivkov (2002) for 25 mm particle board with a half-dowel thickness joint under compressive loading (Derikvand and Ebrahimi 2015). The thickness of the joints also had an important impact on the stiffness of the joint; the stiffness of the joint increased as the diameter of the dowel increased (Záborský et al. 2016).

Table 3 presents the results of the four-factor ANOVA test that evaluated the effect of individual factors and their interaction on the elastic stiffness of the joints. It was clear from the significance level p-value that the thickness of the joints and type of glue were statistically significant factors for the one-factor analysis.

The effect of the loading type in itself was not shown to be statistically significant, and in interaction with all the other factors its effect was insignificant according to the significance level p-value.

The elastic stiffness was affected by the type of loading, thickness of samples (half versus one-third joints), and type of adhesive (PVAc or PUR). The samples were tested under a compressive test, which showed 23% greater elastic stiffness (Fig. 6a) than the tensile loading test. As shown in Fig. 6b, the half-thickness joints exhibited approximately 32% higher elastic stiffness than the one-third thickness joints, whereas in the results for the beech wood, the half-thickness dowel joints had 66.6% higher elastic stiffness compared to the joints with one-third thickness (Záborský et al. 2018). For adhesive type (Fig. 6c), the elastic stiffness of joints bonded with PUR adhesive and tested with both types of loading (compressive and tensile) and both types of joints (half thickness and one third thickness) was 133% higher than that of joints bonded with PVAc adhesive. Figure 6d shows that the elastic stiffness was affected by the growth ring direction, and higher stiffness was achieved with intermediate annual rings, but we can see that there wasn’t statistical significant difference.

Table 3. Multifactor Analysis of Variance for Elastic Stiffness of Wood Joints

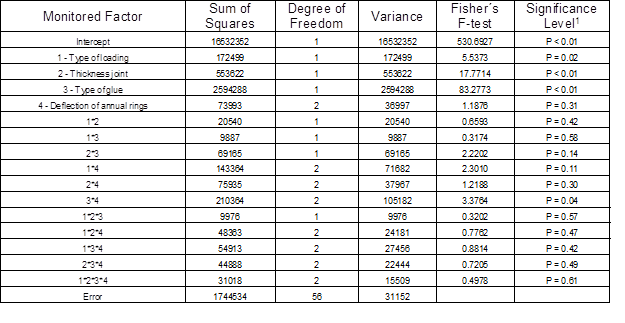
1 Significance was accepted at P < 0.01

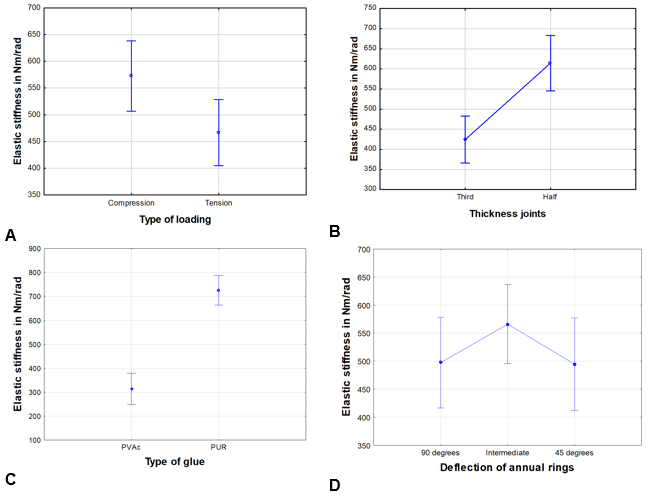
Fig. 6. Graphic visualization of the (A) type of loading; (B) joint thickness; (C) type of glue; and (D) deflection of annual ring on elastic stiffness on mean values of elastic stiffness

Figure 7a shows that with the compressive loading test, the half-thickness joints had approximately 51% higher elastic stiffness than the one-third thickness joints. The effect of the half-thickness joints showed higher elastic stiffness under both types of loading. The elastic stiffness of the joints bonded with PUR and PVAc adhesive (Fig. 7b) was lower under tensile loading as compared to compressive loading. The elastic stiffness of the PVAc adhesive under compressive loading was 38% higher than that under tensile loading, and in the case of PUR adhesive, the elastic stiffness under compressive loading reached a 17% higher value compared with tensile loading. Therefore, the elastic stiffness of joints (half joints and one-third thickness joints) bonded with PVAc and PUR adhesive was higher under compressive loading than under tensile loading.

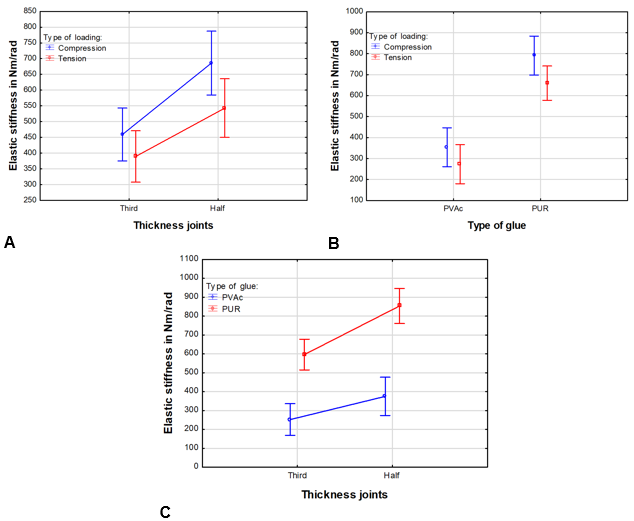
Fig. 7. The effect of (A) joint thickness and type of loading; (B) type of glue and type of loading; (C) joint thickness and type of glue on mean values of elastic stiffness

Figure 7c shows the interaction of the elastic stiffness of joints bonded with PVAc and PUR adhesives with one third and half joint thickness. The elastic stiffness of the one- third joints bonded with PVAc was 46% lower than the PUR adhesive with the one third joint. The elastic stiffness of the half joints with PUR adhesive was 126% higher compared to the joint bonded with PVAc, and similar results were found with tenon joints (Gaff et al. 2018). Thus, in both cases (the half joint and one third thickness joints), the PUR adhesive showed higher values of elastic stiffness compared with the PVAc adhesive.

The elastic stiffness of joints bonded with PVAc (half and one-third thickness joint) under compressive loading (Fig. 8) was 38% higher compared to those under tensile loading, while with PUR adhesive the elastic stiffness was 17% higher for compressive loading. The elastic stiffness of the one-third thickness joints bonded with PUR adhesive under compressive loading was approximately 134% higher compared to that of PVAc, and under tensile loading it was 273% higher. In the case of the half thickness joints bonded with PUR under compressive loading, it was 107% higher compared to PVAc, and with tensile loading that with PUR was 152% higher compared to PVAc. The elastic stiffness of the PUR adhesive bonded with half and one-third thickness joints under both types of loading (compressive and tensile) was 134% higher compared to that for PVAc.

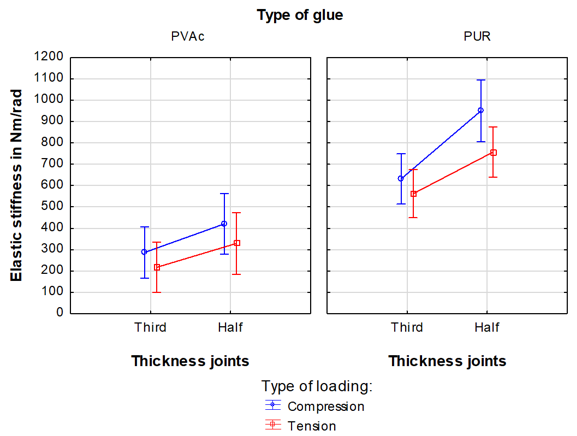
Fig. 8. Synergistic effect of the type of glue, joint thickness, and type of loading on the mean values elastic stiffness

Figure 9 shows correlation between the elastic stiffness and density of wood (r = 0.21), which indicates that the elastic stiffness of dowel joints can be poorly predicted based on the density of wood.

Figure 10 shows that there was a linear dependence between the elastic stiffness and the stiffness at the maximum load. This dependence is expressed by the correlation coefficient r = 0.84, which means that the maximum stiffness of the joint can be predicted based on the elastic stiffness.

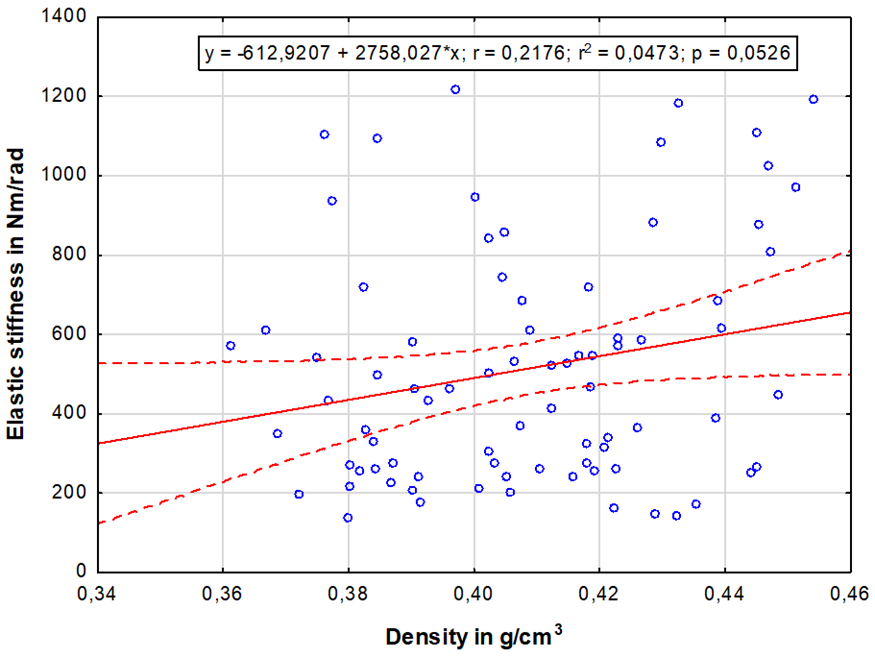
Fig. 9. Dependence of elastic stiffness on density for wood joints

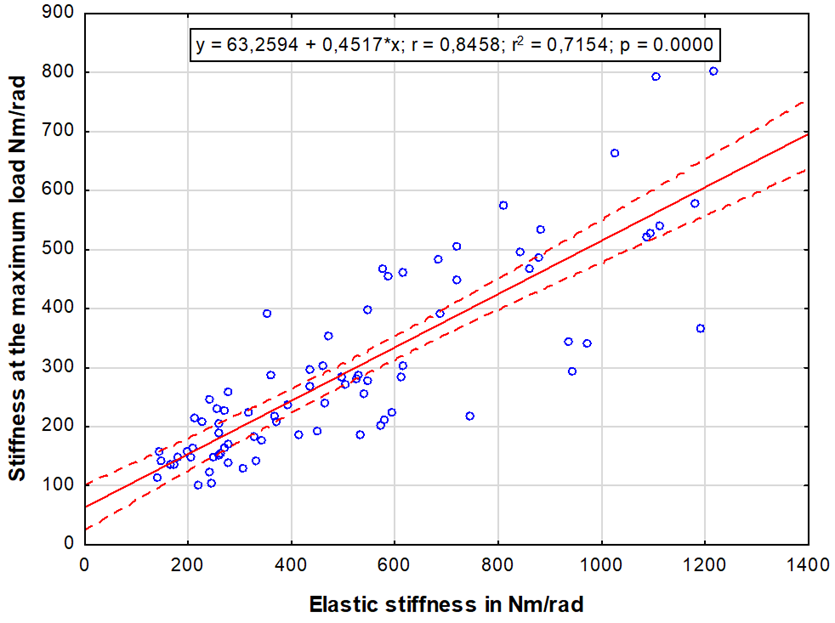
Fig. 10. Dependence of stiffness at the maximum load on elastic stiffness in wood joints

CONCLUSIONS

1. Spruce dowel joints had higher elastic stiffness with PUR adhesive than PVAc, with respect to compressive and tensile loading, with half and one-third joint thickness. The test results revealed that half thickness joints had a higher elastic stiffness than one- third thickness joints.

2. In spite of this result, there were significant differences between the average elastic stiffness of joints glued with PVAc and those glued with PUR; the average elastic stiffness for PUR was approximately twice that of the average value for PVAc.

3. The maximum average elastic stiffness was obtained for half-thickness joints bonded with PUR adhesive under compressive loading, which was 921 Nm/rad, and the minimum average value of elastic stiffness, 209 Nm/rad, was reached in samples with one third thickness joints bonded with PVAc adhesive under tensile loading.

4. Although elastic stiffness varies from joint to joint, the size of the dowel should be standardized. Future studies will have to investigate the elastic stiffness of different species of dowel with different loads (compressive and tensile) and different adhesives.

ACKNOWLEDGMENTS

The authors are grateful for the support of project Advanced Research Supporting the Forestry and Wood-processing Sector’s Adaptation to Global Change and the 4th Industrial Revolution, No. CZ.02.1.01/0.0/0.0/16_019/0000803, financed by OP RDE. The authors are also grateful for the support of the University-wide Internal Grant Agency (CIGA) of the Faculty of Forestry and Wood Sciences, project No. 2016 – 4311.

REFERENCES CITED

Albin, R. (1989). “Durchbiegung und Lastannahmen im Korpusmöbelbau,” Holz als Roh- und Werkstoff 47, 7-10. DOI: 10.1007/BF02612342

ČSN 91 0001 (2007). “Furniture – Technical requirement,” Czech Office for Standards: Metrology and Testing, Prague, Czech Republic.

ČSN 91 0000 (2005). “Furniture – Nomenclature,” Czech Technical Standard, Prague, Czech Republic.

Derikvand, M., and Ebrahimi, G. (2015). “Rotational stiffness of L-shaped joints,” in: The XXVIITH International Conference Research for Furniture Industry, Karaj, Iran, pp 19-26.

Eckelman, C. A. (1989) “Strength of furniture joints constructed through-bolts and dowel-nuts,” Forest Products Journal 39, 41-48.

Eckelman, C.A., Rabiej, R. (1985). “A comprehensive method of analyze of case furniture,” Forest Product Journal 35, 41-48.

Eckelman, C. A., Zhang, J., and Erdil, Y. Z. (2003). “Withdrawal and bending strength of dowel-nuts in plywood and oriented strand board,” Forest Products Journal 53(6), 54-57.

Efe, H., Zhang, J., Erdil, Y. Z., and Kasal, A. (2005). “Moment capacity of traditional and alternative T-type end-to-side-grain furniture joints,” Forest Products Journal 55(5), 69-73.

EN 942 (2007). “Timber in joinery – General requirements,” European Committee for Standardization, Brussels, Belgium.

Fukuyama, H., Ando, N., Inayama, M., Takemura, M., and Inoue, M. (2007). “Proposal of analytical model of wooden dowel shear joint: Single shear joint with slender-type round dowel,” Journal of Structural and Construction Engineering 72(622), 129-136, DOI: 10.3130/aijs.72.129_4

Gaff, M., and Babiak, M. (2017). “Methods for determining the plastic work in bending and impact of selected factors on its value,” Composite Structures 163(1), 410-422. DOI: 10.1016/j.compstruct.2017.11.036

Gaff, M., Vokatý, V., Babiak, M., and Bal, B. (2016). “Coefficient of wood bendability as a function of selected factors,” Construction and Building Materials 126, 632-640. DOI: 10.1016/j.conbuildmat.2016.09.085

Gaff, M., Záborský, V., Kasickova, V., and Borůvka, V. (2018). “The effect of selected factors on domino joint stiffness,” BioResources 13, 2424-2439. DOI: 10.15376/biores.13.2.2424-2439

Hrovatin, J., Zupančič, A., Sernek, M., and Oblak, L. (2013). “The fracture moment of corner joint bonded by different glues,” Drvna Industrija 64(4), 335-340. DOI: 10.5552/drind.2013.1248

İmirzi, H. Ö., Smardzewski, J., and Dongel, N. (2015). “Method for substitute modulus determination of furniture frame construction joints,” Turkish Journal of Agriculture and Forestry 39(5), 775-785. DOI: 10.3906/tar-1406-92

ISO 13061-1 (2014). “Physical and mechanical properties of wood—Test methods for small clear wood samples—Part 1: Determination of moisture content for physical and mechanical tests,” International Organization for Standardization, Geneva, Switzerland.

ISO 13061-2 (2014). “Physical and mechanical properties of wood—Test methods for small clear wood samples—Part 2: Determination of density for physical and mechanical tests,” International Organization for Standardization, Geneva, Switzerland.

Jivkov, V. (2002). “Bending strength and stiffness of some end corner joints from 25 mm laminated particleboard,” in: Nabytok Conference, Slovakia, Zvolen, ISBN 80-228-1193-9.

Kanazawa, F., Pizzi, A. P., Properzi, M., Delmotte, L., and Pichelin, F. (2005) “Parameters influencing wood-dowel welding by high-speed rotation,” Journal of Adhesion Science and Technology 19(12), 1025-1038. DOI: 10.1163/156856105774382444

Loferski, J. R., and Gamalath, S. (1989). “Predicting rotational stiffness and nail joints,” Forest Product Journal 39(7-8), 8-16. ISSN: 0015-7473

Martins, S. A., Menezzi, C. H. S. D., Ferraz, J. M., and Souza, M. R. (2013). “Bonding behavior of Eucalyptus benthamii wood to manufacture edge glued panels,” Maderas. Ciencia y Tecnología 15, 79-92. DOI: 10.4067/S0718-221X2013005000008

Ozcifci, A. (1995). A Study about Resistance Features to Corner Points of Furniture made by Particleboard, M.Sc. Thesis, Gazi University, Institute of Science and Technology, Ankara, Turkey.

Pizzi, A. P., Leban, J. M., Kanazawa, F., Properzi, M., and Pichelin, F. (2004). “Wood dowel bonding by high-speed rotation welding,” Journal of Adhesion Science and Technology 18(11), 1263-1278. DOI: 10.1163/1568561041588192

Podlena, M., and Borůvka, V. (2016). “Stiffness coefficients of mortise and tenon joints used on wood window profile,” BioResources 11(2), 4647-4687. DOI: 10.15376/biores.11.2.4677-4687

Tankut, N. (2007). “The effect of glue and glueline thickness on strength of mortise and tenon joints,” Wood Research 54(4), 69-78.

Vaziri, M., Lindgren, O., Pizzi, A. P., and Mansouri, H. R. (2010). “Moisture sensitivity of Scots pine joints produced by linear frictional welding,” Journal of Adhesion Science and Technology 24(8-10), 1515-1527. DOI: 10.1163/016942410X501098

Warmbier, K., and Wilczynski, A. (2000). “Strength and stiffness of dowel corner joints: Effect of joint dimension,” Folia Forestalia Polonica 31, 29-4. ISSN 0208-5704

Záborský, V., Borůvka, V., Ruman, D., and Gaff, M. (2016). “Effect of geometric parameters of structural elements on joint stiffness,” BioResources 12, 932-946. DOI: .10.15376/biores.12.1.932-946

Záborský, V., Sikora, A., Gaff, M., Kasickova, V., and Borůvka, V. (2018) “Effect of selected factors on stiffness of dowel joint,” BioResources 13(3), 5416-5431. DOI: 10.15376/biores.13.3.5416-5431

Zhang, J. L. (1991). Rational Design of Dowel Joint in Case Construction, Master’s Thesis, Purdue University, West Lafayette, IN, USA.

Article submitted: September 11, 2018; Peer review completed: October 28, 2018; Revised version received: November 13, 2018; Accepted: November 22, 2018; Published: December 14, 2018.

DOI: 10.15376/biores.14.1.1127-1140