Abstract
Non-destructive evaluation (NDE) techniques have been shown to be effective for evaluating mechanical properties of wood-based materials. In this study, transverse vibration of a beam under the two ends free boundary condition (FBV) was employed to measure the modulus of elasticity (MOE) in different strength directions of laminated strand lumber (LSL). It was found that the MOE values measured by the FBV were slightly higher than those measured using the three-point bending test (TPB), and the correlation coefficients between the MOE values along the major and minor strength directions measured by the two methods were 0.845 and 0.938, respectively. The effect of the length/depth ratio on measured MOE values by the FBV method was also investigated. With the decrease in the length/depth ratio of LSL, the measured MOE in the major and minor strength directions decreased. The results of the ANOVA test showed that the length/depth ratios had a significant effect on the measured MOE. The experimental values of MOE of LSL in the diagonal strength direction matched well with the theoretical values calculated by the Hankinson-type formula.
Download PDF
Full Article
Evaluation of Modulus of Elasticity of Laminated Strand Lumber by Non-Destructive Evaluation Technique
Zhiqiang Wang,a,* Jianhui Zhou,b Meng Gong,b Ying Hei Chui,b and Xiaoning Lu a
Non-destructive evaluation (NDE) techniques have been shown to be effective for evaluating mechanical properties of wood-based materials. In this study, transverse vibration of a beam under the two ends free boundary condition (FBV) was employed to measure the modulus of elasticity (MOE) in different strength directions of laminated strand lumber (LSL). It was found that the MOE values measured by the FBV were slightly higher than those measured using the three-point bending test (TPB), and the correlation coefficients between the MOE values along the major and minor strength directions measured by the two methods were 0.845 and 0.938, respectively. The effect of the length/depth ratio on measured MOE values by the FBV method was also investigated. With the decrease in the length/depth ratio of LSL, the measured MOE in the major and minor strength directions decreased. The results of the ANOVA test showed that the length/depth ratios had a significant effect on the measured MOE. The experimental values of MOE of LSL in the diagonal strength direction matched well with the theoretical values calculated by the Hankinson-type formula.
Keywords: Laminated strand lumber; Modulus of elasticity; Strength directions; Length/ depth ratio; Non-destructive evaluation
Contact information: a: College of Materials Science and Engineering, Nanjing Forestry University, Nanjing 210037, China; b: Faculty of Forestry and Environment Management, University of New Brunswick, Fredericton, NB E3B 5A3, Canada; *Corresponding author: wangzhiqiang@njfu.edu.cn
INTRODUCTION
Laminated strand lumber (LSL) is one of the most innovative and versatile wood building products available. It is an attractive alternative to solid sawn lumber because it exhibits better mechanical and physical properties than solid lumber of the same wood species, as well as less variability (Moses et al. 2003). This revolutionary product is used for a broad range of applications including rim board, millwork, and window, door, and garage door headers, as well as for many industrial purposes. New uses for this product are still evolving, including the use of LSL for vertical members in commercial structural applications where the framing member heights are long and the wind loads are substantial (Canadian Wood Council 2015). Previous studies focused on basic manufacturing technology, physical property evaluation, and improvement, especially regarding the effect of strand alignment on material mechanical properties and product development of LSL (Moses et al. 2003; Joscak et al. 2006; Me et al. 2008; Zhang and Lu 2014). Despite some stiffness prediction models (Moses et al. 2003; Zhang and Lu 2014), only the modulus of elasticity (MOE) in the major strength direction was reported (Denizli-Tankut et al. 2004). Very little information about the MOE of LSL in different strength directions is available.
Non-destructive evaluation (NDE) techniques, such as transverse vibration or flexural vibration, have been found effective for evaluating mechanical properties of wood-based materials. The vibration testing of wood has been studied for a long time for a variety of purposes, such as mechanical grading. Some early research was reviewed and the theoretical derivations were given by Hearmon (1966). Chui (1991) presented a simplified method for simultaneous evaluation of MOE and the shear modulus of wooden beams, which was performed by measuring the two natural frequencies of a beam via a free-free beam vibration. This method was also used for non-destructive testing of laminated and unlaminated, reconstituted wood panels used for furniture manufacture (Ilic and Ozarska 1996). Hu and Hsu (1996) found that the span-to-depth ratio was a critical factor for the application of the transverse free-free beam vibration technique.
More recently, Yoshihara (2011; 2012a; 2012b; 2012c) did a series studies about the specimen configurations and analysis method in the flexural vibration tests of solid wood and wood-based materials. Yoshihara reported that the MOE was independent of the specimen depth/length ratio; however, the in-plane shear modulus was significantly dependent on the specimen depth/length ratios. The specimen configuration and lamination construction did not significantly affect the measurement of the MOE of plywood by flexural vibration tests. In contrast, shear modulus decreased as the depth/ length ratio of the specimen decreased. Biechele et al. (2011) compared four different NDE methods for assessing the mechanical properties of unjointed and finger-jointed lumber. They found that the stiffness values of unjointed and finger-jointed lumber measured by all NDE methods correlated well with values measured by the static bending test. Liu et al. (2014) found that the width of the lumber did not have a significant effect on the MOE measured by the free beam vibration method.
In order to investigate the MOE values of LSL, the free beam vibration (FBV) method was employed for measuring the MOEd (MOE measured by non-destructive tests) values of LSL. The accuracy of the FBV method was verified by the static MOEs from three-point bending test. The MOEd values in different strength directions, namely major, minor, and diagonal strength directions, were tested using the FBV method. The effect of the length/depth ratio on measured MOEd values by the FBV method was investigated. The relationship among the MOE values was also studied. The results can be used for the structural application of LSL products and further improvement of the FBV method for evaluating engineered wood products.
EXPERIMENTAL
Materials
LSL panels used in this study were provided by Weyerhaeuser with the dimensions of 2.44 m (length) × 1.22 m (width) and a nominal thickness of 38 mm. The LSL panels were manufactured from strands of aspen poplar (Populus tremuloides) with isocyanate-based binder adhesive. In order to evaluate the influences of strength directions, namely with surface wood fiber angles of 0° (major strength direction), 45° (diagonal strength direction), and 90° (minor strength direction), as indicated in Fig.1, and length/depth ratios of the specimen on measured MOE values, eight groups of specimens were randomly cut from four LSL panels. The specimen information is listed in Table 1. All test specimens were kept in a conditioning room at a temperature of 20 °C and a relative humidity of 65% for 40 days before testing. The average moisture content and density after conditioning was 7.88% with standard deviation (SD) of 0.32% and 729 kg/m3 with SD of 13.06 kg/m3, respectively.
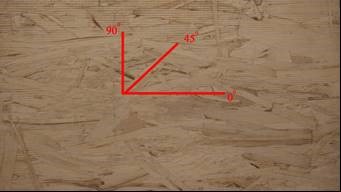
Fig. 1. Defined strength direction of LSL
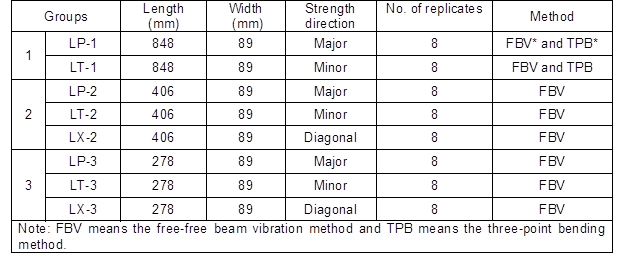
Table 1. Experiment Design and Specimen Information
Free-Free Beam Vibration (FBV) Method
The Free-Free Beam Vibration (FBV) technique is based on the transverse vibration of a beam under two ends free boundary condition. The specimens in all groups were first tested by the FBV method. The setup consisted of an instrumented hammer, an accelerometer, and a spectrum analyzer, as shown in Fig. 2. The impact and acceleration time signals were recorded by a data acquisition device, and the frequency response function (FRF) was calculated from the time signals using data analysis software (RT Pro Photon, Brüel & Kjær, Denmark). The fundamental natural frequency of each specimen was measured under free-free boundary condition by impact vibration testing. The specimens were hung with two springs at 0.224 times its length from both ends, which were the two nodes of the first mode, to minimize the effect of the springs. The dimensions and mass of each specimen were measured before vibration testing. The MOEd was calculated based on the transverse vibration of the Euler beam theory, as indicated in Eq. 1 (Biechele et al. 2011),
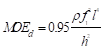 (1)
(1)
where the MOEd is the dynamic modulus of elasticity (MPa), ρ is the density (kg/m3), f1 is the first natural frequency (Hz), l is the length of the specimen (m), and h is the depth of the specimen (m).
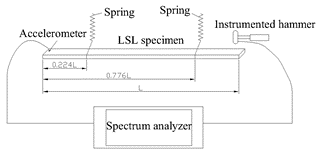
Fig. 2. Setup illustration of the free beam vibration (FBV) test
Three-Point Bending (TPB) Method
Specimens of group LP-1 and LT-1 were used for the three-point bending tests on a universal mechanical test machine according to ASTM D 198-09 (2009). Each specimen was tested under flatwise bending with a span of 700 mm and a speed of 0.3 mm/min to obtain its MOEs. The mid-span deflection (Δ) was measured using a 25 mm linear variable differential transformer (LVDT) up to the target load. The MOEs obtained by the TPB method was calculated using Eq. 2,
![]() (2)
(2)
where the MOEs is the modulus of elasticity by static tests (MPa), P is the applied load (N), Δ is deflection at mid-span (mm), P/Δ is calculated from the elastic proportion of load-displacement curve by curve fitting, l is the span (mm), b is the specimen width (mm), and h is the specimen depth (mm).
RESULTS AND DISCUSSION
Correlation of MOE Values by FBV and TPB Methods
The correlation of MOE values of groups LP-1 and LT-1 measured by the FBV and TPB methods is illustrated in Fig. 3.
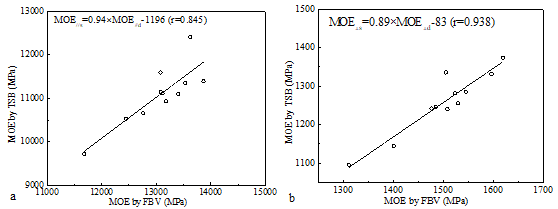
Fig. 3. Relationships of MOE values in the major (a) and minor (b) strength directions measured by TPB and FBV methods
It can be seen that the FBV results agreed with TPB results for both strength directions to some degree. The MOEd values were slightly higher than the MOEs values, which followed a similar trend as other research studies (Biechele et al. 2011; Liu et al. 2014). Overall, the correlation of the MOE values in the minor strength direction between FBV and TPB methods was better than that in the major strength direction. The correlation coefficients (r values) for the MOE values in the major and minor strength directions were 0.845 and 0.938, respectively.
Effect of Length/Depth Ratio on MOE Values by FBV Method
The mean MOE values measured by both the FBV and TPB methods and their coefficient of variations are summarized in Table 2.
Table 2. Descriptive Data of MOE Values
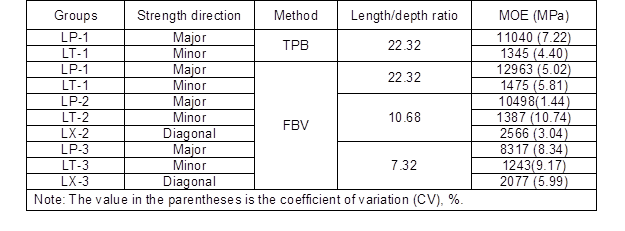
The effect of the length/depth ratio on the measured MOEd values, also referred to as the apparent dynamic MOE, in both major and minor strength direction is illustrated in Fig. 4. As the length/depth ratios increased from 7.32 to 22.32, the measured MOEd// (dynamic MOE in the major strength direction) and MOEd⊥ (dynamic MOE in the minor strength direction) increased from 8452 to 13036 MPa and from 1239 to 1493 MPa, respectively (Fig. 4). The reason is thought to be the effect of shear deformation and rotary inertia on the beam flexure vibration. The influence of shear deformation and rotatory inertia increases with decreasing length/depth ratio (Chui and Smith 1990). A length/depth ratio over 15 is recommended for the ‘Euler beam’-based FVB method. When testing lumber with a small length/depth ratio, the influence of shear deformation and rotatory inertia should be considered based on the Timoshenko beam theory (Chui 1991). The ANOVA tests on the effect of the length/depth ratio on measured MOE values are shown in Table 3. For all measured MOE values, the p values were less than 0.05, which means that the length/depth ratios exhibited significant effects on the measured MOE values. The results verified the findings above. Comparisons between the two groups shows that the MOEd// values of three length/depth ratios are different. Based on the correlation between dynamic and static results, a length/depth ratio at 22.32 is appropriate for MOEd// measurement. The difference of MOEd⊥ values between group LT-1 and LT-2 was not obvious at the 0.05 level, while group LT-1 vs. LT-3 and group LT-2 vs. LT-3 showed an obvious difference at the same level. Therefore, the effect of length/depth on the MOEd⊥ was found to be significant for length/depth ratio of 7.32 or less in this study. These findings differ from those of Yoshihara (2012c), in which the length/depth ratio was reported to have no effect on the measured MOE by FBV method.
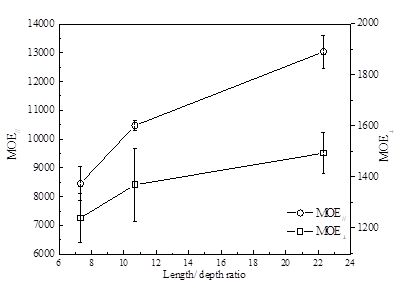
Fig. 4. The effect of the length/depth ratio on measured MOEd in the major and minor strength directions
Table 3. Statistical Analysis of the Length/Depth Ratio on Measured MOEd

Relationships of MOEd in Various Strength Directions
It was reported that the relationship between the MOE in the major and minor strength directions and the MOE on an angle can be expressed by a Hankinson-type formula, as shown in Eq. 3 (Bodig and Jayne 1982),
![]() (3)
(3)
where N is the MOE at the angle θ from the major direction, Q is the MOE in the major strength direction, P is the MOE in the minor strength direction, and n is an empirically determined constant that is equal to 2 (Bodig and Jayne 1982).
Using this formula, the MOEd in the diagonal strength direction can be predicted with the measured MOEd values in the major and minor strength directions. The MOEd values of groups LP-2 and LT-2, and LP-3 and LT-3 were used for predicting the corresponding MOEd values in the diagonal strength direction of groups LX-2 and LX-3, respectively. As shown in Table 4, the relative errors between the measured and predicted MOEd values in the diagonal strength direction were within 5.0%. The results were in agreement with the measured MOEd values in the diagonal direction by the FBV method.
Table 4. Comparison of Measured and Predicted MOEd in the Diagonal Strength Direction
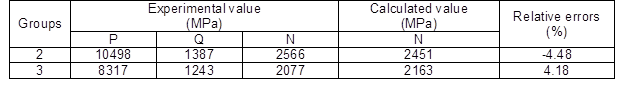
CONCLUSIONS
- It can be concluded that the FBV method can be used for measuring the MOEd values of LSL. This FBV method agrees with the TPB method in determination of MOE of LSL; however, special care should be taken for the length/depth ratios of specimens.
- The MOEd values measured by FBV were slightly higher than those measured using the static bending method, and the correlation coefficients between the MOE values measured by the two methods were 0.845 and 0.938 for MOE// and MOE⊥, respectively.
- With the increase of the length/depth ratios of the LSL specimen from 7.32 to 22.32, the measured MOE// and MOE⊥ increased from 8452 to 13036 MPa and from 1239 to 1493 MPa, respectively.
- The length/depth ratios investigated in this study exhibited a significant effect on the measured MOEd, the apparent MOE, which may have been caused by the effect of shear deformation and rotary inertia on the beam flexure vibration.
- The Hankinson-type formula was shown to be able to predict the diagonal MOE of LSL using measured dynamic MOE// and MOE⊥
ACKNOWLEDGMENTS
The authors wish to acknowledge Jiangsu Government Scholarship for Overseas Studies, the National Natural Science Foundation of China (Grant No. 31570559), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), and the Jiangsu Science and Technology Project (Grant No. BY2014006-05). The authors would also like to thank Weyerhaeuser for testing materials.
REFERENCES CITED
ASTM D198-09. (2009). “Standard test methods of static tests of lumber in structural sizes,” American Society for Testing and Materials, West Conshohocken, PA, USA.
Biechele, T., Chui, Y. H., and Gong, M. (2011). “Comparison of NDE techniques for assessing mechanical properties of unjointed and finger-jointed lumber,” Holzforschung 65(3), 397-401. DOI:10.1515/hf.2011.038
Bodig, J., and Jayne, B. A. (1982). Mechanics of Wood and Wood Composites, New York: Van Nostrand Reinhold Company.
Canadian Wood Council. (2015) “Laminated Strand Lumber,” (http://cwc.ca/wood-products/structural-composite/laminated-strand-lumber/).
Chui, Y. H., and Smith, I. (1990). “Influence of rotatory inertia, shear deformation and support condition on natural frequencies of wooden beams,” Wood Sci. Tech. 24(3), 233-245. DOI: 10.1007/BF01153557
Chui, Y. H. (1991). “Simultaneous evaluation of bending and shear moduli of wood and the influence of knots on these parameters,” Wood Sci. Tech. 25(2), 125-134. DOI: 10.1007/BF00226812
Denizli-Tankut, N., Smith, L. A., Smith, W. B., and Tankut, A. N. (2004). “Physical and mechanical properties of laminated strand lumber treated with fire retardant,” For. Prod. J. 54(6), 63.
Hearmon, R. F. S. (1966). “Vibration testing of wood,” For. Prod. J. 16(8), 29-39.
Hu, L. J., and Hsu, W. E. (1996). “Implementation of transverse simple beam vibration technique to determine MOE for wood based materials: accuracy, comparability, and limitations,” in: Proc. Intl. Symp. Nondestructive Testing of Wood, 247-258.
Ilic, J., and Ozarska, B. (1996). “Nondestructive evaluation of properties of reconstituted wood products used in Australia,” in: Proceedings from the International Symposium on Nondestructive Testing of Wood, 269-278.
Joscak, T., Teischinger, A., Mueller, U., and Mauritz, R. (2006). “Production and material performance of long-strand wood composites-Review,” Wood Res. 51(3), 37-49.
Liu, Y., Gong, M., Li, L., and Chui, Y. H. (2014). “Width effect on the modulus of elasticity of hardwood lumber measured by non-destructive evaluation techniques,” Constr. Build. Mater. 50, 276-280. DOI:10.1016/j.conbuildmat.2013.09.029
Me, C., Peng, M., and Zhou, D. (2008). “Study on laminated strand lumber from poplar,” in: Proceedings from the Conference on Engineered Wood Products Based on Poplar/Willow Wood, 25-31.
Moses, D. M., Prion, H. G. L., Li, H., and Boehner, W. (2003). “Composite behavior of laminated strand lumber,” Wood Sci. Tech. 37(1), 59-77. DOI:10.1007/s0026-003-0169-5
Yoshihara, H. (2011). “Measurement of the Young’s modulus and shear modulus of in-plane quasi-isotropic medium-density fiberboard by flexural vibration,” BioResources 6(4), 4871-4885. DOI: 10.15376/biores.6.4.4871-4885
Yoshihara, H. (2012a). “Examination of the specimen configuration and analysis method in the flexural and longitudinal vibration tests of solid wood and wood-based materials,” For. Prod. J. 62(3), 191-200. DOI: 10.13073/0015-7473-62.3.191
Yoshihara, H. (2012b). “Influence of specimen configuration on the measurement of the off-axis Young’s modulus of wood by vibration tests,” Holzforschung 66(4), 485-492. DOI:10.1515/hf.2011.182
Yoshihara, H. (2012c). “Influence of the specimen depth to length ratio and lamination construction on Young’s modulus and in-plane shear modulus of plywood measured by flexural vibration,” BioResources 7(1), 1337-1351. DOI: 10.15376/biores.7.1.1337-1351
Zhang, H., and Lu, X. (2014). “Modeling of the elastic properties of laminated strand lumber,” Wood Res. 59(1), 1-10.
Article submitted: May 26, 2015; Peer review complted: August 24, 2015; Revisions received and accepted: October 29, 2015; Published: November 24, 2015.
DOI: 10.15376/biores.11.1.626-633
