Abstract
The aim of this paper was to predict the static bending modulus of elasticity (MOES) and modulus of rupture (MOR) of Scots pine (Pinus sylvestris L.) wood using three nondestructive techniques. The mean values of the dynamic modulus of elasticity based on flexural vibration (MOEF), longitudinal vibration (MOELV), and indirect ultrasonic (MOEUS) were 13.8, 22.3, and 30.9 % higher than the static modulus of elasticity (MOE S ), respectively. The reduction of this difference, taking into account the shear deflection effect in the output values for static bending modulus of elasticity, was also discussed in this study. The three dynamic moduli of elasticity correlated well with the static MOE S and MOR; correlation coefficients ranged between 0.68 and 0.96. The correlation coefficients between the dynamic moduli and MOE S were higher than those between the dynamic moduli and MOR. The highest correlation between the dynamic moduli and static bending properties was obtained by the flexural vibration technique in comparison with longitudinal vibration and indirect ultrasonic techniques. Results showed that there was no obvious relationship between the density and the acoustic wave velocity that was obtained from the longitudinal vibration and ultrasonic techniques.
Download PDF
Full Article
Evaluation of Stiffness and Strength of Scots Pine Wood Using Resonance Frequency and Ultrasonic Techniques
Khaled T. S. Hassan,a,b,* Petr Horáček,a and Jan Tippnera
The aim of this paper was to predict the static bending modulus of elasticity (MOES) and modulus of rupture (MOR) of Scots pine (Pinus sylvestris L.) wood using three nondestructive techniques. The mean values of the dynamic modulus of elasticity based on flexural vibration (MOEF), longitudinal vibration (MOELV), and indirect ultrasonic (MOEUS) were 13.8, 22.3, and 30.9 % higher than the static modulus of elasticity (MOES), respectively. The reduction of this difference, taking into account the shear deflection effect in the output values for static bending modulus of elasticity, was also discussed in this study. The three dynamic moduli of elasticity correlated well with the static MOES and MOR; correlation coefficients ranged between 0.68 and 0.96. The correlation coefficients between the dynamic moduli and MOES were higher than those between the dynamic moduli and MOR. The highest correlation between the dynamic moduli and static bending properties was obtained by the flexural vibration technique in comparison with longitudinal vibration and indirect ultrasonic techniques. Results showed that there was no obvious relationship between the density and the acoustic wave velocity that was obtained from the longitudinal vibration and ultrasonic techniques.
Keywords: Nondestructive testing; Indirect ultrasonic; Longitudinal vibration; Flexural vibration; Density
Contact information: a: Mendel University in Brno, Faculty of Forestry and Wood Technology, Department of Wood Science, Zemědělská 3, 61300Brno,Czech Republic.; b: Alexandria University, Faculty of Agriculture, Department of Forestry and Wood Technology, Aflaton st., El-Shatby 21545, Alexandria, Egypt; *Corresponding author: xsoliman@node.mendelu.cz; khaledtaha85@gmail.com
INTRODUCTION
Nondestructive materials evaluation (NDE) is the approach of evaluating physical and mechanical characteristics of the material without changing its end-use performance (Ross et al.1998). The instruments used for nondestructive evaluation can be applied widely at different processing levels, starting from wood-based composites to standing trees (Lin et al. 2006). Usually NDE is carried out using three methods, ultrasonic, stress waves, or resonant frequency vibrations (Ilic 2001a). The acoustics study commonly used in the area of wood and wood-based materials is solid acoustics in the audible (20 Hz to 20 kHz) and ultrasound (> 20 kHz) frequency ranges (Smith 2001).
The ultrasonic moduli of elasticity determination depend on the ultrasonic wave speed and density. The ultrasonic velocities range from 1000 to 2000 m.s-1 perpendicular to the grain direction and from 5000 to 6000 m.s-1 parallel to the grain direction of solid wood; the radial velocity is approximately 50% higher than the tangential velocity (Beall 2002).
The common mode shapes of a vibrating beam are longitudinal, flexural, and torsional vibrations. They are the dynamic equivalents of static tension, bending, and torsion (Bucur 2006). The classical destructive bending evaluation of modulus of elasticity is time- and money-consuming when applied to standing trees. This may lead to reduced opportunities for determining the optimal use of the produced wood from standing trees (Ilic 2003).
Modulus of elasticity (MOE) is a property that describes the material stiffness. A high value of wood MOE indicates that the wood has a high resistance to deformation (Liang and Fu 2007). Several studies have considered the relationships between the dynamic and static modulus of the elasticity of wood; some of these are reported by Liu et al. (2006), who investigated the dynamic modulus of wood using the transverse and longitudinal vibration techniques. They showed a significant linear correlation between the static MOE and the dynamic MOEobtained from both techniques. Sales et al. (2011) ascertained the accuracy of the ultrasonic and transverse vibration techniques for evaluating the static bending modulus of elasticity. The authors indicated that the values of the coefficient of determination for the ultrasonic technique and for transverse vibration were significant and that both techniques were valid tools for the nondestructive evaluation of the MOE of structural timber pieces. However, few reports have considered the comparison of resonance frequency and ultrasonic techniques for predicting the modulus of rupture of Scots pine wood. The acoustic wave velocity transmission through timber can be affected by several factors, such as moisture content, temperature, grain orientation, density, decay, and geometry (Beall 2002).
The main objective of this study was to investigate the dynamic modulus of elasticity of Scots pine wood by flexural vibration, longitudinal vibration, and indirect ultrasonic techniques, and to evaluate the degree of the association between the dynamic MOE obtained by the three different techniques with the static MOE and MOR.
EXPERIMENTAL
Materials
The experiments were carried out using 40 specimens of Scots pine (Pinus sylvestris L.). The dimensions of each specimen were 20 mm x 60 mm in the cross section and 500 mm in length. The dynamic modulus of elasticity was determined for each specimen using ultrasonic and resonance vibration techniques. After the nondestructive evaluation, the specimens were tested in a static bending test.
Methods
Flexural and longitudinal vibration techniques
The specimens were supported by rubber threads, and the flexural and longitudinal vibrations were induced by impacting the specimen with a hammer, as shown in Fig. 1, for each test. An ultra-linear measurement condenser microphone Behringer (type ECM8000) and afire-wire external soundcard (Edirol FA-101 with 24- bit/192 kHz sampling frequency) were used for recording the signal.
The longitudinal and flexural vibration frequencies were measured by a Fast Fourier Transform (FFT) analyzer.
The dynamic longitudinal and flexural vibration moduli of elasticity were calculated according to Equations 1 and 2 (Ilic 2001b; Cho 2007),
where MOELV is the dynamic modulus of elasticity based on longitudinal vibration, MOEF is the flexural dynamic modulus of elasticity, is the frequency of longitudinal vibration, is the fundamental frequency of the free-free flexural vibration in the first mode, is the specimen length, is the wood density, is the radius of gyration of the cross section, and (4.73) is a constant corresponding to the first mode of free-free flexural vibration.
Fig. 1. Test set-up for longitudinal vibration (a) and flexural vibration (b)
Ultrasonic technique
Measurements of the ultrasonic velocities were made with a Portable Ultrasonic Nondestructive Digital Indicating Tester (PUNDIT). The device, equipped with two 150 kHz piezo-electric transducers (transmitting and receiving transducer), generates an ultrasonic impulse by electronic excitation of the transducer. There are three test set-ups that can be used to measure the ultrasonic velocity using PUNDIT; they are the direct, indirect, and semi-direct measurements (Fig. 2). The measurements were conducted in this study with only the indirect (surface) method. In order to estimate the exact length of the transmission path, a series of measurements with the transducers at different distances were performed.
Fig. 2. Direct, indirect, and semi-direct ultrasonic measurements
The ultrasonic velocity was calculated using the following equation (Bucur 2006),
(3)
where is the ultrasonic wave velocity (m.s-1), L is the specimen length (m), and t is the transit time (s). The dynamic modulus of elasticity based on indirect ultrasonic was determined through the one dimensional wave equation as follows (Bucur 2006),
(4)
where MOEUS is the dynamic modulus of elasticity based on indirect ultrasonic (Pa), is the ultrasonic wave velocity (m.s-1), and ρ is the density of wood (kg.m-3).
Torsional vibration
The test was performed using the apparatus used in flexural vibration; the microphone was placed above the end at one corner of the sample and the torsional vibration was established by hitting the other end at the corner as described in (Nakao and Okano 1987). The shear modulus value was calculated from the following equation (Cho 2007),
(5)
where G is the shear modulus, is thetorsional vibration frequency at thefirst mode, n is the mode number,
is the wood density,
is the polar moment of inertia, and
= 0.141bh3(b and h are the cross-sectional dimensions).
Static bending properties
Static bending tests were conducted according to BS 373 (British Standard Institution 1957) using a universal testing machine (Zwick testing machine, model no. Z050).The wood specimens were equilibrated to a MC of 12% at 20°C and 65% relative humidity.
The wood density at 12% moisture content was determined from the weight and volume of the specimens. The values of the static bending modulus of elasticity were recalculated as described in Teranishiet al. (2008), by taking into account the value of the shear deflection in the center-load bending test according to Equation 6,
(6)
where Etrue is the static bending without the shear deflection effect, , ES is the static bending MOE, G is the shear modulus, h is specimen depth, and isthespan of bending.
The mean values of density, acoustic wave velocity, and their descriptive statistics are shown in Table 1.
Table 1. Physical Characteristics of Scots Pine Wood
* CV is the coefficient of variation
It was observed that the average ultrasonic velocity (VUS) was higher than those obtained from longitudinal vibration (VLV). Several researchers have reported that the longitudinal wave velocity by ultrasonic techniques was higher than the longitudinal vibration techniques (Baar et al. 2012; Bucur 2006). Machado et al. (2009), in a study on three wood species, reported that the indirect ultrasonic method of testing had lower values than that using the direct method. However, a strong relationship existed between both, with an R2 value of 0.90.Thus, the difference between the ultrasonic and longitudinal vibration wave velocity will increase when using the direct method. In addition, the direct method cannot be applied to wood members in-service, because the ends of the wood would be unavailable (Machado and Palma 2011).
The mean values of the static bending properties, modulus of elasticity without shear deflection effect (MOEtrue), shear modulus, and the dynamic modulus of elasticity determined by the three testing techniques, and their descriptive statistics of Scots pine wood are shown in Table 2.
Table 2. Mean Values of Modulus of Rupture, Static Modulus of Elasticity, Shear Modulus, and Dynamic Modulus of Elasticity
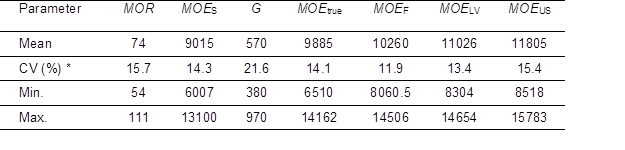
All values are in (N.mm-2); * CV is coefficient of variation
The mean values of the dynamic modulus of elasticity based on flexural vibration (MOEF), longitudinal vibration (MOELV), and indirect ultrasonic (MOEUS) were 13.8, 22.3, and 30.9% higher than the static modulus of elasticity (MOES), respectively. These findings were in agreement with those obtained by other researchers, indicating that the dynamic MOE values obtained by the NDT techniques were higher than those from the static tests.
Haines et al. (1996) reported that the mean value of Young’s modulus obtained from the ultrasonic method exceeded the MOE by about 17 to 22%. Wang et al. (2008) observed that the mean values of the dynamic MOE by the ultrasonic method were greater than those of the static MOE by 7.1%, 16.1%, 14.2%, and 9.0% for Japanese cedar, Taiwania, Douglas fir, and Southern pine, respectively. Smulski (1991) reported that the dynamic MOE values for maple, birch, ash, and oak were on average 22, 27, 23, and 32% higher than the observed values of the static MOE, respectively. Yang et al. (2002) found that the longitudinal resonance MOE was 39% and it was 36% higher than the static MOE for the clear and decayed wood, respectively. The difference between the dynamic and the static modulus of elasticity is attributed to the visco-elastic behavior and damping properties of wood. When a force is applied for a very short duration, wood exhibits elastic behavior, and when a force is applied for longer time, wood then behaves as a viscous material (Halabe et al. 1997).
Figures 3 to 5 show that the correlation coefficients (r) between the static modulus of elasticity (MOES), and the dynamic modulus of elasticity determined by the flexural vibration, the longitudinal vibration, and the indirect ultrasonic techniques, were 0.96, 0.86, and 0.73, respectively, indicating strong correlations.
The developed regression models were statistically significant at the 0.05 confidence level for all of the relationships. Several studies have shown a good relationship between the dynamic modulus of elasticity and the static modulus of elasticity of wood (Ross and Pellerin1994; Yang et al. 2002; Ross et al. 2005; Wang et al. 2008).
In general, the values obtained from the resonance vibration (flexural and longitudinal) tests were found to be near to the MOE values, rather than those obtained by the ultrasonic test. Moreover, the regression models showed that the correlation coeffi-cients (r) between MOEs and the resonance vibration MOE (flexural and longitudinal) were higher than those between MOEs and the ultrasonic MOE.
Fig. 3. Relationship between MOEF and MOES
Fig. 4. Relationship between MOELV and MOES
Fig. 5. Relationship between MOEUS and MOES
The observed relationships were similar to the findings of Liang and Fu (2007), who reported that the dynamic MOE obtained from the resonance frequency by the Fast Fourier Transform (FFT) technique was closer to the static MOE and gave a higher precision degree than the ultrasonic and stress wave techniques. Ilic (2003) concluded that the resonance vibration techniques are useful for providing an indication of the MOE of wood. Ilic (2001b) reported that for uniform wood materials, vibration techniques are characterized by simplicity, speed, and ease of use. The presented results showed that the flexural vibration MOE gave the highest correlation coefficient in comparison with the other two nondestructive techniques.
In the present results, to reduce the difference between the static and dynamic MOE values, a special method was applied to the static bending values (Equation 6). This method takes into account the value of the shear deflection in the center-load bending test.
Fig. 6. Relationship between MOEF and MOEtrue
Fig. 7. Relationship between MOELV and MOEtrue
Fig. 8. Relationship between MOEUS and MOEtrue
By using this method, the difference between the dynamic and static modulus of elasticity was reduced. The mean values of the dynamic modulus of elasticity based on flexural vibration (MOEF), longitudinal vibration (MOELV), and the indirect ultrasonic (MOEUS) were 3.8, 11.5, and 19.4% higher than the true static modulus of elasticity (MOEtrue), respectively. Figures 6 to 9 show significant correlations among the MOEtrue and the dynamic modulus determined by the three different nondestructive techniques. Teranishiet al. (2008) conducted a study on 30 hardwood and five softwood species to reduce the difference between the static modulus and the longitudinal vibration modulus of elasticity; they used the values of the static bending MOE without the effect of shear deflection. The differences between the static and dynamic MOE before and after the shear deflection was taken into account were 27 and 20%, respectively. Cho (2007) conducted a linear regression relationship between the true static Young’s modulus and the flexural vibration modulus of elasticity based on Timoshenko’s beam theory; the results illustrated the almost-perfect agreement between the two methods used.
As shown in Table 3, the three nondestructive techniques were well correlated with the static results for rupture testing (MOR). The correlation coefficients between the static modulus of rupture (MOR) and the dynamic modulus determined by flexural vibration, longitudinal vibration, and ultrasonic techniques were 0.90, 0.75, and 0.68, respectively. The highest correlation was obtained with the flexural vibration test.
Table 3. Coefficients of Linear Regression Formulas (Y = a + bX) for the Correlation between Modulus of Rupture and the Dynamic Elastic Modulus Values
r, correlation coefficient
Several studies have indicated good correlations between the static MOR and the dynamic modulus of elasticity of Scots pine wood. Horáček et al. (2012) reported a significant correlation between the static bending properties and the dynamic modulus of elasticity for Scots pine wood. The correlation coefficient was r = 0.96 and r = 0.74 for MOES and MOR, respectively.
The results shown inFigs.3 to 5 and Table 3 indicated that the correlation coeffi-cients between the dynamic and static MOE were higher than those between the dynamic MOE and static MOR. The developed regression models were statistically significant at the 0.05 confidence level for all of the relationships.
In order to investigate the behavior of the acoustic wave velocity due to the change in wood density, a simple regression analysis was used. Figure 9 illustrated the relationship between the wood density and the longitudinal wave velocity by ultrasonic and longitudinal vibration techniques.
In contrast to the one-dimensional wave beam theory, it was noted that there was an independent association between Scots pine wood density and the acoustic wave velocity. These results are compatible with the findings in literature by Baar et al. (2012), who investigated the effect of wood density on five tropical hardwoods. They showed thata change in the sound wave velocity due to a change in density could not be confirmed for any of the species. Smulski (1991) found no meaningful correlation between the stress wave velocity and the specific gravity for four northeastern US hardwoods.
Mishiro (1995) examined the effect of density on the ultrasonic velocity in the three anatomical directions on seven softwoods and 12 hardwoods. He reported that although the ultrasonic velocity in the longitudinal direction was independent of the density as a whole, it could be divided into three groups; (1) ultrasonic velocity increased with increasing density, (2) independent of density, (3) decreased with increasing density.
Fig. 9. Relationship between density and acoustic wave velocity
On the other hand, Oliveira and Sales (2006) observed an increasing trend in the longitudinal ultrasonic velocity as the density of Brazilian tropical woods increased. Ilic (2003) indicated that the microfibrils angle (S2 layer) can control the propagation of the stress waves through wood. In addition, wide ray parenchyma cells may influence the propagation by altering the fiber direction away from the longitudinal direction and may decrease the wood stiffness. Gerhards (1982), in his state-of-the-art review, reported several factors affected the stress wave transit in lumber, such as temperature, moisture content, and decay.
It is possible that heterogeneity and the variability nature of wood had a role in this behavior. Further studies of additional parameters such as grain angle, temperature, and moisture content, together with density could give a better understanding of the behavior of the acoustic wave velocity through timber.
CONCLUSIONS
- The evaluation of static bending properties (MOE and MOR) of Scots pine wood using flexural vibration, longitudinal vibration, and indirect ultrasonic non-destructive techniques was studied. The mean values of the dynamic modulus of elasticity based on flexural vibration (MOEF), longitudinal vibration (MOELV), and indirect ultrasonic (MOEUS) were 13.8, 22.3, and 30.9% higher than the static modulus of elasticity (MOES), respectively.
- This difference was reduced by taking the shear deflection effect into account for static bending tests. There were good significant correlations between the static bending properties (MOES and MOR) and the dynamic modulus of elasticity obtained by vibration and ultrasonic techniques, indicating that the three techniques are valid methods for the prediction of the actual modulus of elasticity and the modulus of rupture of Scots pine wood. The correlation coefficients between the dynamic and static MOE were higher than those between dynamic MOE and static MOR. It was noted that there was an independent association between Scots pine wood density and acoustic wave velocity.
ACKNOWLEDGMENTS
The authors are grateful to the Faculty of Forestry and Wood Technology, Mendel University in Brno, through the Internal Grant Agency (IGA) project, the Ministry of Education, Youth, and Sports of the Czech Republic, Project No. 6215648902, and the European Social Fund and the state budget of the Czech Republic, project “The Establishment of an International Research Team for the Development of New Wood-based Materials” reg. no. CZ.1.07/2.3.00/20.0269 for financial support.A special thanks goes to Brno University of Technology, Faculty of Civil Engineering for providing the ultrasonic instrument.
REFERENCES CITED
Baar, J., Tippner, J., and Gryc, V. (2012). “The influence of wood density on longitudinal wave velocity determined by the ultrasound method in comparison to the resonance longitudinal method,” European Journal of Wood and Wood Products 70(5), 767-769.
Beall, F. C. (2002). “Overview of the use of ultrasonic technologies in research on wood properties,” Wood Sci. Technol. 36(3),197-212.
BS 373(1957). “British standard: Methods of testing small clear specimens of timber,” British Standard Institution, London.
Bucur, V. (2006). Acoustics of Wood, CRC Press, New York, pp. 420.
Cho, C.L. (2007). “Comparison of three methods for determining Young’s modulus of wood,”Taiwan Journal of Forest Science 22(3), 297-306.
Gerhards, C. C. (1982). “Longitudinal stress waves for lumber stress grading: Factors affecting applications: State of art,” For. Prod. J. 32(2), 20-25.
Haines, D. W., Leban, J. M., and Herbe, C. (1996). “Determination of Young’s modulus for spruce, fir and isotropic materials by the resonance flexure method with comparisons to static flexure and other dynamic methods,” Wood Sci. Technol. 30(4), 253-263.
Halabe, U. B., Bidigalu, G. M., GangaRao, H. V. S., and Ross, R. J. (1997). “Nondestructive evaluation of green wood using stress wave and transverse vibration techniques,” Mater. Eval.55(9), 1013-1018.
Horáček, P., Tippner, J., and Hassan, K. T. (2012). “Nondestructive evaluation of static bending properties of Scots pine wood using stress wave technique,” Wood Research 57(3), 359-366.
Ilic, J. (2001a). “Variation of the dynamic elastic modulus and wave velocity in the fibre direction with other properties during the drying of Eucalyptus regnans F. Muell.,” Wood Sci. Technol. 35, 157-166.
Ilic, J. (2001b). “Relationship among the dynamic and static elastic properties of air dry Eucalyptus delegatensis R. Baker,” HolzRoh- Werkstoff59(3), 169-175.
Ilic, J. (2003). “Dynamic MOE of 55 species using small wood beams,” HolzRoh- Werkstoff61(3), 167-172.
Liang, S.-Q., and Fu, F. (2007). “Comparative study on three dynamic modulus of elasticity and static modulus of elasticity for Lodgepole pine lumber,” Journal of Forestry Research18(4), 309-312.
Lin, C. J., Tsai, M. J., and Wang, S. Y. (2006). “Nondestructive evaluation techniques for assessing dynamic modulus of elasticity of moso bamboo (Phyllosachys edulis) lamina,”J. Wood Sci. 52, 342-347.
Liu, Z., Liu, Y., Yu, H., and Juan, J. (2006). “Measurement of the dynamic modulus of elasticity of wood panels,” Frontiers of Forestry in China 1(4), 245-430.
Machado, J., Palma, P., andSimões, S. (2009). “Ultrasonic indirect method for evaluating clear wood strength and stiffness,” Proceedings of the 7th International Symposium on Non-destructive Testing in Civil Engineering, 969-974.
Machado, J. S., and Palma, P. (2011). “Non-destructive evaluation of the bending behavior of in-service pine timber structural elements,” Mater. Struct. 44(5), 901-910.
Mishiro, A. (1996). “Effect of density on ultrasonic velocity in wood,”Mokuzai Gakkaishi 42(9), 887-894.
Nakao, T., and Okano, T. (1987). “Evaluation of modulus of rigidity by dynamic plate shear testing,” Wood Fiber Sci. 19, 332-338.
Oliveira, F. G. R., and Sales, A. (2006).“ Relationship between density and ultrasonic velocity in Brazilian tropical woods,” Bioresour. Technol. 97(18), 2443-2446.
Ross, R., Brashaw, B. K., and Pellerin, R. F. (1998).“Nondestructive evaluation of wood,” For. Prod. J.48(1), 14-19.
Ross, R. J., Zerbe, J. I., Wang, X., Green, D. W., and Pellerin, R.F. (2005). “Stress wave nondestructive evaluation of Douglas-fir peeler cores,” For. Prod. J.55(3), 90-94.
Ross, R. J., and Pellerin, R. F. (1994). “Nondestructive testing for assessing wood members in structures, A review,” USDA Forest service Forest Products Laboratory, General Tech. Rep. FPL-GTR-70.
Sales, A., Candian, M., and Cardin, V. S. (2011). “Evaluation of the mechanical properties of Brazilian lumber (Goupia glabra) by nondestructive techniques,” Construction and Building Materials 25(3), 1450-1454.
Smith, W.R. (2001). “Wood: Acoustic properties,” In: Encyclopedia of Materials: Science and Technology, Elsevier Science Ltd., London, 9578-9583.
Smulski, S. J. (1991). “Relationship of stress wave-and static bending determined properties of four northeastern hardwoods,” Wood and Fiber Science 23(1), 44-57.
Teranishi, M., Koizumi, A., and Hirai, T. (2008). “Evaluation of quality indexes of bending performance and hardness for hardwoods,” J. Wood Sci. 54(5), 423-428.
Wang, S. Y., Chen, J. H., Tsai, M. J., Lin, C. J., and Yang, T. H. (2008). “Grading of softwood lumber using nondestructive techniques,” Journal of Materials Processing Technology 208(1-3), 149-158.
Yang, J. L., Ilic, J., and Wardlaw, T. (2002).“Relationships between static and dynamic modulus of elasticity for a mixture of clear and decayed eucalypt wood,” Australian Forestry 66(3), 193-196.
Article submitted: December 7, 2012; Peer review completed: January 7, 2013; Revised version received and accepted: February 2, 2013; Published: February 6, 2013.
