Abstract
This research was conducted to determine the impact bending strength and dynamic bending strength of Norway spruce wood from Slovenia. An accelerometer was added to the impact pendulum in order to capture the material’s response to an instantaneous load. Impact bending strength of specimens were determined by standard method measuring the height of pendulum before and after the break. While measuring the impact pendulum decelerations during the fracture of the specimen, the impact bending strength and dynamic bending strength was calculated. Correlations between the measured properties were determined, for which the R2 was in the range 0.88 to 0.51 between the standard and accelerometer method and between the impact bending strength and dynamic bending strength, respectively. The results confirmed that the methods used to determine the impact bending strength were comparable and that it was possible to determine dynamic bending strength on the basis of impact pendulum deceleration measurement.
Download PDF
Full Article
Impact and Dynamic Bending Strength Determination of Norway Spruce by Impact Pendulum Deceleration
Dominika Gornik Bučar * and Miran Merhar
This research was conducted to determine the impact bending strength and dynamic bending strength of Norway spruce wood from Slovenia. An accelerometer was added to the impact pendulum in order to capture the material’s response to an instantaneous load. Impact bending strength of specimens were determined by standard method measuring the height of pendulum before and after the break. While measuring the impact pendulum decelerations during the fracture of the specimen, the impact bending strength and dynamic bending strength was calculated. Correlations between the measured properties were determined, for which the R2 was in the range 0.88 to 0.51 between the standard and accelerometer method and between the impact bending strength and dynamic bending strength, respectively. The results confirmed that the methods used to determine the impact bending strength were comparable and that it was possible to determine dynamic bending strength on the basis of impact pendulum deceleration measurement.
Keywords: Wood; Spruce; Impact bending strength; Dynamic bending strength; Impact pendulum; Acceleration
Contact information: University of Ljubljana, Biotechnical Faculty, Department of Wood Science and Technology, Jamnikarjeva 101, SI-1000 Ljubljana, Slovenia;
* Corresponding author: Dominika.gornik@bf.uni-lj.si
INTRODUCTION
Spruce wood is a frequently used wood species in timber structures, and all structural timber must be strength-graded using various non-destructive methods. The methods used to determine the strength of a material are based on measuring various material properties using different methods of capturing such measurements. The assessed piece can be strength-graded on the basis of the measured values (modulus of elasticity, density, knot area ratio, etc.) by considering the known correlations. In the past, a lot of research has addressed structural timber behaviour under sustained loads, or what is known as the duration of load effect. Structural timber is most frequently strained in this way in practical applications (e.g., a wooden roof assembly loaded with snow).
Structural timber can also be exposed to instantaneous loads, such as an earthquake, explosions, a car crashing into a wooden guard rails (Jansson 1992; Leijten 2000), or a load falling on the structure, whereby the impact velocity is significantly higher than in the standard short (static) duration test.
The resistance of wood to impact loading involves the impact bending strength. The time component is important, since the impact load is instantaneous. A material with higher impact resistance is tougher, while wood with a lower impact bending strength is more brittle. The impact bending strength of solid bodies depends on the ability to accumulate and dissipate energy at deformation. In this respect, tough materials are able to accumulate more energy than brittle ones. The work exerted at the maximum (final) load equals the total energy received at impact load (Kollmann 1984).
The behaviour of wood under impact loading appears to be physically different from the behaviour under static loading (Mindess and Madsen 1986; Jannson 1992). Not only have there been relatively few studies of this kind, but also the validity of the old test data is questioned, as the latest test results show different results (Leijten 2000). Therefore, there is a lack of data regarding the toughness of structural timber (solid or/and laminated) concerning the source of raw material and/or correlations to the non-destructively determined properties. Sukontasukkul et al. (2000) reported similar conclusions, stating that there is not enough information on the impact bending properties of PSL (parallel strand lumber), which makes its design problematic in the face of impact loading conditions. In these cases engineers commonly use the information of mechanical properties that are obtained by non-destructive testing, and in case of instantaneous load, greater strength is considered as required by standard static conditions.
Siewert et al. (1999) provide a detailed overview of the development and significance of impact bending strength determination methods, stressing that the methods have become reliable and reproducible. Impact bending strength tests were among the first types of dynamic tests (Bodig and Jayne 1982) since the Hatt-Turner test was used in the early years of the past century. Leijten (2004) states that the mean impact bending strength is, in most cases, lower than the static bending strength. He also stated that the impact strength is wood species- and grade-dependent.
Sonderegger and Niemz (2004) ascertained bending and tensile strengths, as well as the impact bending strength of Norway spruce (Picea abies Karst.) wood with compression failures present. Failures of this type appear in raw materials that have been, for instance, exposed to inclement weather. They reported up to 40% lower impact bending strength compared to the samples without compression failure. De Palacios et al. (2008) studied differences in the impact bending strength of Scots pine wood (Pinus sylvestris L.), depending on the position of the specimen in the tree. They found that the impact bending strength increased with distance from the pith, and it decreased with the height of the specimen-taking point.
Riesco Munoz and Remacha Gete (2011), who studied correlations between the various mechanical properties of oak (Quercus robur) timber, asserted the relative independence of hardness and impact bending strength as regards other mechanical properties. They reported very low correlations (R2values only around 0.25) between impact bending strength and static bending.
Impact bending strength, as well as some other mechanical properties of wood, increase with density. However, unlike other mechanical properties, it increases with moisture content, since green wood is more flexible than dry wood. Impact bending strength is also influenced by fiber orientation, and in conifers it is higher in a radial than in a tangential direction. In wood-based products, such as laminated veneer lumber (LVL), sample orientation has been found to influence the toughness (Bao et al. 2001; Bal and Bektaş 2012; Bal 2014). It was reported that impact bending strength is greater in a flatwise direction than in an edgewise direction. The cited authors attributed this discrepancy to the LVL structure of multiple glue lines that resulted in the adhesive restricting the absorbing action of the contiguous veneers, thereby reducing the impact toughness in the edgewise direction.
An important factor is also the temperature of wood. The impact bending strength of spruce wood with moisture content over 20% increases with temperature, while the influence of the temperature of wood with moisture content between 8 and 20% on impact bending strength is more complex (Kollmann 1984). The wood density is also important in this case.
Kubojima et al. (2000), who studied bending strength and toughness of heat-treated Sitka spruce (Picea sitchensis Bong.), stated that heat-treated wood became more brittle in the impact bending test. The absorbed energy in impact bending increased in the initial stage of heat treatment and decreased later. A similar finding was also reported by Bal and Bektas (2012), who compared factors influencing the impact bending strength of laminated veneer lumber (LVL) produced from eucalyptus (Eucalyptus grandis W. Hill ex Maiden), poplar (Populus x euramericana I-214), and beech (Fagus orientalis L.) wood, as well as solid wood. They found that the impact bending values of solid beech and eucalyptus wood were higher than those of LVL made of beech and eucalyptus veneer, but no differences were found between the impact bending values of LVLs made of poplar and solid poplar wood. They stated that one of the reasons for this could be the steaming process, which could have negatively influenced the impact bending. Takashi and Yasushi (2005) reported a significantly lower impact bending strength of Japanese larch (Larix kaempferi Carriere) specimens that were subjected to high-temperature kiln drying.
Sukontasukkul et al. (2000) found that under impact loading, the absorbed energy by the PSL specimens was higher than during static loading. As the impact velocity increased, the absorbed energy decreased, due perhaps to the greater degree of local damage.
The results of recent research (Dündar et al. 2012) where non-destructive evaluation of some mechanical properties of wood using thermal conductivity was investigated, indicated a significant linear correlation between the coefficient of thermal conductivity (CTC) and the specific gravity, the modulus of rupture, the modulus of elasticity, and the impact bending strength (IBS) of fir (Abies nordmanniana), black pine (Pinus nigra), and beech (Fagus orientalis) wood. The reported correlations between CTC and IBS on fir wood R2=0.62, on black pine wood R2=0.71, and beech R2=0.70.
EXPERIMENTAL
198 boards of Norway spruce (Picea abies Karst.) from Slovenia region were visually strength-graded (SIST DIN 4074-1:2009) to meet the requirements for structural timber. From each board, two specimens with an oriented cross-section, parallel strands, and no defects (knots, resin pockets, cracks, reaction wood, etc.) of 10 x 10 mm cross-section, were cut. The specimens were conditioned to a moisture content of 10%, weighed, and their dimensions measured within an accuracy of 0.01 mm. On base of these data the density and the ring width of each specimen was determined. Each specimen was tested by impact bending strength device (Fig. 1) according to DIN 52189 (1981) and
- Impact bending strength measuring initial and final angle of pendulum – referred as standard method impact bending strength
- Impact bending strength measuring the deceleration of pendulum during impact – referred as deceleration method impact bending strength
- Dynamic bending strength were determined.
1. Standard method impact bending strength
The height of the impact pendulum rise following the break and/or the initial and final angle of the pendulum were measured as shown in Fig. 1. The impact bending strength was calculated according to Eq. 1,
(1)
where T is toughness (work on specimen), wp is the weight of the pendulum, L is the distance from the centre of support to the pendulum’s centre of gravity, A1 is the angle of entry (initial angle), and A2 is the final angle when the pendulum travels across the break.
2. Deceleration method impact bending strength
An accelerometer (Brüel and Kjaer, Denmark) was mounted on the impact pendulum as shown in Figure1 to capture decelerations during pendulum impacts. An AT-MIO 16-E1 data acquisition card (National Instruments, USA) with a sampling frequency of 100 kHz was used to record voltage from the amplifier to which the accelerometer was connected. The signal captured was filtered by a Bessel low-pass filter of the 20th order and with a frequency of 500 Hz. National Instruments’ LabView software was used for capture and filtering. The decelerations were integrated by the trapezoidal method (Glyn 2004) using Eq. 2,
(2)
where an is the nth measurement of deceleration, t is the time of sampling, and vn is nth speed. The initial speed v0 is the speed at which the pendulum hits the specimen. It equals 4.7 m/s as calculated according to the following equation (Eq. 3),
(3)
where g is gravitational deceleration, and h is the difference in height between the initial height of the pendulum and the height of specimen. The distance or increment xn was calculated using Eq. 4:
. (4)
The impact bending strength is calculated as total work exerted or energy put in the break performed using the equation (Eq. 5),
(5)
where k is the number of measurements in each set. Fn is the instantaneous force calculated using the equation,
(6)
and mp is the mass of impact pendulum, which was 9.3 kg.
3. Dynamic bending strength
The dynamic bending strength is calculated the same way as static bending strength (Kollmann 1984) using the equation
(7)
where Fmax is maximum failure force calculated according to Eq. 6, 
is dynamic bending strength, lis the distance between specimen support, and a and h is specimen width and height respectively.
Fig. 1. Schematics of experiment, A1 – initial angle, A2 – angle after the break, L – distance from the centre of support to the pendulum’s centre of gravity
To verify the the correlation between the methods for impact bending strength determination, the concordance correlation coefficient (Lin 1989) using the following equation was calculated,
(8)
where
and Y1 in Y2 are standard method impact bending strength and deceleration method impact bending strength, respectively.
RESULTS AND DISCUSSION
The results of measurements presented Fig. 2 show that the deceleration method impact bending strength is comparable to standard method impact bending strength, which is confirmed also by the high R2 with the value of 0.88. The same can be concluded with the calculated concordance correlation coefficient with the value of 0.907. The figure shows that the values of standard method impact bending strength were slightly higher than the deceleration method impact bending strength. The difference of approximately 5% is attributed to better accuracy when the deceleration method is used.
Fig. 2. Correlation of standard method impact bending strength and deceleration method impact bending strength
The correlation between the density of specimens and deceleration method impact bending strength is shown in Fig. 3. These results confirm reports from the literature (Kollmann 1984) that impact bending strength increases with specimen density. Correlations were not particularly high (R2=0.25), but they were clear. Although some specimens (except that from extreme) had high density (550 kg/m3), they exhibited very low impact bending strength (30 kJ/mm2). Figure 3 shows that a majority of specimens’ density ranged from 400 to as much as 530 kg/m3, which also confirms the data in Table 1 with calculated average density and standard deviation of 451.34 kg/m3 and 46.21 kg/m3, respectively, whereas the deceleration method impact bending strength ranged from 15 to 70 kJ/mm2 with average value and standard deviation of 34.53 kJ/mm2 and 11.65 kJ/mm2, respectively. The individual values of density went up to an extreme of 600 kg/m3, where the deceleration method impact bending strength also went up to almost 90 kJ/mm2.
Fig. 3. Correlation between the density and deceleration method impact bending strength
Table 1. Average Values and Standard Deviations for Measured Values
The mechanical properties of wood also depend on the ring width, and in conifers, narrower rings also mean better mechanical properties like toughness. Figure 4 shows a trend of increasing toughness with decreasing ring width. A similar finding was reported by Kollmann (1984) for spruce wood, while De Palacios et al. (2008) reported a statistically significant relationship between ring width and the quantity of energy absorbed at dynamic response of Scots pine wood and that the variation is greater in the case of wider rings. Adamopoulos and Passialis (2010), who studied the correlation between the modulus of elasticity and toughness of solid Norway spruce specimens with wide rings (3.6 mm average width) and narrow rings (1.6 mm average width), report better correlation in the case of narrow rings (r = 0.884 narrow rings and r = 0.546 wide rings, respectively).
Fig. 4. Correlation between annual ring widths and deceleration method impact bending strength
The correlations between dynamic bending strength and deceleration method impact bending strength of specimens are presented in Fig. 5. The correlations with the linear and nonlinear (polynomial) relationship are presented with the correlation coefficients of 0.51 and 0.57, respectively. Beside the greater correlation coefficient, one also can visually judge that the polynomial relationship was better, especially in the region between the 20 and 60 kJ/mm2. In the greater values of deceleration method impact bending strength, it was harder to evaluate which type of relationship was better due to the insufficiency of data.
The figure clearly shows their interdependence, which has also been stated by other authors. Sonderegger and Niemz (2004) reported a coefficient of determination of R2 = 0.33 when comparing impact bending strength with the dynamic MOE calculated on the basis of sound velocity by Norway spruce, while Munoz (2011) reported low correlations (R2 values only around 0.25) between impact bending strength and static bending or compression variables, which were attributable to the different nature (static vs. dynamic) of the measured properties. Average dynamic bending strength in our research amounted to around 97.25 MPa with a standard deviation of 19.66 MPa. Considering the average static bending strength of Norway spruce wood for specimens without defects that Leijten (2004) states as 82.1 MPa, and the argument that dynamic bending strength is 20-30% higher than static tests (Leijten 2004), the present measurements of dynamic bending strength correspond with this. In addition, it is also necessary to take into consideration the influence of inertial forces, since the impact pendulum has to accelerate the specimen in a relatively short period of time.
Fig. 5. Correlation between dynamic bending strength and deceleration method impact bending strength
As already mentioned in connection with the correlation between the density and deceleration method impact bending strength (Fig. 3), some of the specimens had significantly increased density as well as deceleration method impact bending strength. A detailed analysis of the deviating specimens established that the specimens with greater density and deceleration method impact bending strength in Fig. 3 also deviated in Fig. 4 with distinctly narrower rings and increased deceleration method impact bending strength or in Fig. 5 with increased deceleration method impact bending strength and dynamic bending strength.
CONCLUSIONS
- The impact bending strength measurement method based on measuring of deceleration of impact pendulum is comparable to the standard method impact bending strength measurement, in which the impact pendulum height before and after the break is measured. This can be concluded from a high value of coefficient of determination (R2=0.88) and also from a high value of concordance correlation coefficient (
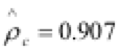). The method with the accelerometer is much more accurate compared to the visual reading of pendulum angle before and after impact. Beside that the method with the accelerometer can be automated. - Impact pendulum decelerations can also be used to calculate the maximum force by means of which the dynamic bending strength can be calculated.
- It can also be confirmed that impact bending strength increases with the density of Norway spruce wood but decreases with the width of rings.
- The correlation between dynamic bending strength and deceleration method (or also standard method) impact bending strength of specimens is good (R2 = 0.51).
REFERENCES CITED
Adamopoulos, S., and Passialis, C. (2010). “Relationship of toughness and modulus of elasticity in static bending of small clear spruce wood specimens,” Eur. J. Wood Prod. 68(1), 109-111. DOI: 10.1007/s00107-009-0365-6
Bal, B. C., and Bektaş, İ. (2012). “The effect of some factors on the impact bending strength of laminated veneer lumber,” BioResources 7(4), 5855-5863. DOI: 10.15376/biores.7.4.5855-5863
Bal, B. C. (2014). “Some physical and mechanical properties of reinforced laminated veneer lumber,” Construction and Building Materials 68, 120-126. DOI: 10.1016/j.conbuildmat.2014.06.042
Bao, F., Fu, F., Choong, E. T., and Hse, C. (2001). “Contribution factor of wood properties of tree poplar clones to strength of laminated veneer lumber,” Wood Fiber Sci. 33(3), 345-352.
Bodig, J., and Jayne, B. A. (1982). Mechanics of Wood and Wood Composites, Van Nostrand Reinhold Company Inc., London.
DIN 52189-1. (1981). “Testing of wood; Impact bending test; determination of impact bending strength,” Deutsches Institut für Normung, Berlin.
De Palacios, P., García Esteban, L., Guindeo, A., Gracía Fernández, F., Canteli Fernández, A., and Navarro, N. (2008). “Variation of impact bending in the wood of Pinus sylvestris L. in relation to its position in the tree,” For. Prod. J. 58(3), 55-60.
Dündar, T., Kurt, S., As, N., and Uysal, B. (2012). “Nondestructive evaluation of wood strength using thermal conductivity,” BioResources 7(3), 3306-3316.
Glyn, J. (2004). Advanced Modern Engineering Mathematics, Pearson Prentice Hall, Harlow, England.
Jansson, B. (1992). “Impact loading of timber beams,” Master’s Thesis, Faculty of Civil Engineering, University of British Columbia, Vancouver, Canada.
Leijten, Ad. J. M. (2000). “Literature review of impact strength of timber and joints,” Proceedings of the World Conference on Timber Engineering, Whistler, BC.
Leijten, A. J. M. (2004). “Heat treated wood and the influence on the impact bending strength,” Heron49(4), 349-359.
Lin, L. I-K. (1989). “A concordance correlation coefficient to evaluate reproducibility”. Biometrics 45 (1), 255–268. DOI:10.2307/2532051.
Kollmann, F. F. P., and Cote, W. A. (1984). Principles of Wood Science and Technology. Volume I.: Solid Wood, Springer-Verlag, Berlin.
Kubojima, Y., Okano, T., and Ohta, M. (2000). “Bending strength and toughness of heat-treated wood,” J. Wood Sci. 46(1), 8-15. DOI: 10.1007/BF00779547
Mindess, S., and Madsen, B. (1986). “The fracture of wood under impact loading,” Material and Structures 19(109), 49-53. DOI: 10.1007/BF02472310
Riesco Munoz, G., and Remacha Gete, A. (2011). “Relationships between mechanical properties of oak timber (Quercus robur L.),” Holzforschung 65(5), 749-755. DOI: 10.1515/hf.2011.053
Siewert, T. A., Manahan, M. P., MCowan, M. P., Holt, J. M., Marsh F. J., and Ruth, E. A. (1999). “The history and importance of impact testing, pendulum impact testing: A century of progress,” ASTM STP 1380, ASTM International, West Conshohocken, PA, United States.
Sonderegger, P., and Niemz, P. (2004). “The influence of compression failure on the bending, impact bending and tensile strength of spruce wood and the evaluation of non-destructive methods for early detection,” Holz Roh Werkst.. 62(5), 335-342. DOI: 10.1007/s00107-004-0482-1
Sukontasukkul, P., Lam, F., and Mindess, S. (2000). “Fracture of parallel strand lumber (PSL) under impact loading,” Materials and Structures 33(7), 445-449. DOI: 10.1007/BF02480664
Takashi, T., and Yasushi, N. (2005). “Impact bending strength of small specimens cut from Japanese larch timber kiln-dried by the high-temperature setting method,” Eurasian J. For. Res. 8(2), 105-110.
Article submitted: January 27, 2015; Peer review completed: May 8, 2015; Revisions accepted: June 9, 2015; Published: June 15, 2015.
DOI: 10.15376/biores.10.3.4740-4750