Abstract
The most effective method for producing fermentable sugars (FSs) from biomass is thermochemical pretreatment assisted by enzymatic hydrolysis. However, the enzymatic hydrolysis-assisted thermochemical pretreatment method is limited by the formation of fermentation inhibitors, and it is time-consuming. There is growing interest in using a microwave (MW) pretreatment due to its uniform and rapid heating. This study aimed to determine, perform data-driven modeling, and optimize the effect of MW combined with dilute acid pretreatment (MW-DA) on the production of FSs from hazelnut shells. An artificial neural networks (ANNs) model based on Box-Behnken Design (BBD) was the best model described for fermentable sugar extraction (FSE). Optimization via BBD-based ANNs model was carried out for an acid concentration of 0.5 to 2% (w/w), a pretreatment time of 5 to 25 min, a pressure of 5 to 15 bar, and a temperature of 120 to 160 °C. The optimized FSE was estimated at 374 mg/g (81.4% conversion efficiency), with a severity factor of 3.61 under 1.58% H2SO4 for 13 min at 160 °C and 8.5 bar. Using the MW-DA pretreatment process lowered the costs significantly due to the decreases in acid concentration and pretreatment time.
Download PDF
Full Article
Improvement of Fermentable Sugar Extraction from Hazelnut Shells through Microwave Assisted Dilute Acid Pretreatment
Sibel Uzuner
The most effective method for producing fermentable sugars (FSs) from biomass is thermochemical pretreatment assisted by enzymatic hydrolysis. However, the enzymatic hydrolysis-assisted thermochemical pretreatment method is limited by the formation of fermentation inhibitors, and it is time-consuming. There is growing interest in using a microwave (MW) pretreatment due to its uniform and rapid heating. This study aimed to determine, perform data-driven modeling, and optimize the effect of MW combined with dilute acid pretreatment (MW-DA) on the production of FSs from hazelnut shells. An artificial neural networks (ANNs) model based on Box-Behnken Design (BBD) was the best model described for fermentable sugar extraction (FSE). Optimization via BBD-based ANNs model was carried out for an acid concentration of 0.5 to 2% (w/w), a pretreatment time of 5 to 25 min, a pressure of 5 to 15 bar, and a temperature of 120 to 160 °C. The optimized FSE was estimated at 374 mg/g (81.4% conversion efficiency), with a severity factor of 3.61 under 1.58% H2SO4 for 13 min at 160 °C and 8.5 bar. Using the MW-DA pretreatment process lowered the costs significantly due to the decreases in acid concentration and pretreatment time.
DOI: 10.15376/biores.18.1.613-628
Keywords: Microwave pretreatment; Severity; Fermentable sugar; Valorization
Contact information: Department of Food Engineering, Izmir Institute of Technology, 35430, İzmir, Turkey * Corresponding author: sibeluzuner@iyte.edu.tr
GRAPHICAL ABSTRACT

INTRODUCTION
The use of agro-food waste products is a potential alternative for maintaining sustainable development and aiming for zero production of waste. Turkey has a rich agricultural biomass stream, and one of its most important agricultural products is hazelnut (Ozcimen and Ersoy-Mericboyu 2010). Hazelnut shells, a residue of hazelnut processing, offers a terrific opportunity for the production of value-added products. Hazelnut shells are currently used either as boiler fuel or landscaping (Atland 2015). Turkey has rich biomass and biomass energy potential (9.5 GW in Turkey) (Şenol 2019). Physicochemical properties such as calorific value, temperature of ignition, and relatively low ash content showed that hazelnut shells are suitable for the production of biofuels (Hebda et al. 2018). Moreover, annual biogas production potential of hazelnut shells in Giresun, city of Turkey, was found to be 38.21 GW h/yr (Şenol 2019). Generating value-added products from hazelnut shells can improve both economic and environmental benefits for producers and consumers of hazelnuts in the region. Uzuner and Cekmecelioglu (2014) reported that hazelnut shells can be utilized as a raw material for pectinase production by performing acid pretreatment and enzymatic saccharification of cellulose and hemicellulose to obtain reducing sugars for fermentation.
The bioconversion of lignocellulosic biomass requires changing the structure of biomass residues and improves the rate and yield of reducing sugars by the use of pretreatment methods. Pretreatment can be divided into three main categories as physical, chemical, and biological. Physical pretreatment processes have proven to be energetically unviable, while biological pretreatment methods can be time-consuming (Chen et al. 2007; Xu et al. 2010). Most of these pretreatment processes require high temperature, high pressure, and/or long operation time to improve the yield of reducing sugars (Zhang et al. 2016). The dilute acid pretreatment at elevated high temperatures is the most commonly used to pretreat biomass (Mesa et al. 2020). However, this method has disadvantages. For instance, degradation products such as furan derivatives and phenolic compounds are generated, and they act as inhibitors during fermentation (Yu et al. 2018). Thus, this method needs a neutralization step before fermentation.
Microwave-assisted pretreatment processing has become increasingly popular due to direct and rapid heating (Zhu et al. 2016). Microwave pretreatments showed higher saccharification yield compared to a steam explosion at the same temperature and shorter reaction time. Moreover, the concentration of inhibitors is decreased drastically (Li et al. 2016). The other important thing is the amount of energy consumed during pretreatments. Vintila et al. (2019) demonstrated that the energy balance was effective for microwave pretreatment of alkaline suspension of sweet sorghum bagasse compared with the steam treatment. During the microwave assisted dilute acid (MW-DA) pretreatment, cellulose is partially decomposed at elevated temperature, hemicelluloses are degraded in weak acids, and lignin is decomposed at elevated pressure and temperature (Hendriks and Zeeman 2009). Lu et al. (2011) reported that the glucose yield of rape straw achieved after microwave pretreatment followed by enzymatic hydrolysis was 56.2%. Ethaib et al. (2016) identified the effect of microwave-assisted dilute acid pretreatment followed by enzymatic hydrolysis of sago palm bark on monosaccharide yield and total reducing sugar. Huang et al. (2017) found that microwave-assisted alkali extraction enhanced enzymatic hydrolysis of bagasse on hemicellulose yield; 86.8% of hemicellulose was extracted in bagasse during the microwave-assisted alkali extraction process enhanced with enzymatic hydrolysis. The study conducted by Sombatpraiwan et al. (2019) determined the optimum conditions for microwave-assisted alkali pretreatment of cassava rhizome followed by enzymatic hydrolysis. Glucose yields were determined as 16.95 g/100 g native cassava rhizome for 48 h hydrolysis under 840 W microwave power, 9-min irradiation time, and 3% w/v NaOH concentration. Rajeswari et al. (2020) focused on the delignification of Aloe vera rind by MW-assisted acid pretreatment followed by enzymatic saccharification. A three-fold decrease was observed in recalcitrant lignin at 480 W during the MW acid pretreatment process in comparison with untreated aloe vera rind biomass. Mikulski and Klosowski (2020) evaluated microwave-assisted dilute acid pretreatment of wheat and rye stillage followed by enzymatic hydrolysis. The highest cellulose hydrolysis obtained was 75% after 24 h at 54 psi for 15 min. Most studies on the pretreatment process are integrated with enzymatic saccharification for releasing reducing sugars. However, the enzymatic saccharification process is costly and time-consuming (Jang and Choi 2018). Although many previous studies have been conducted on the delignification and hemicellulose solubilization of lignocellulosic materials under microwave pretreatment, the same cannot be said about fermentable sugar production.
The MW-DA pretreatment conditions should be optimized for reducing the acid concentration, heating time, fermentation inhibitors, and increasing the recovery of fermentable sugar from biomass. This study evaluated the effective FSE from hazelnut shells by MW-DA pretreatment process using Box-Behnken Response Surface Methodology (RSM). The information obtained is critical to demonstrate the full potential of hazelnut shells as feedstock for bioprocessing applications. The objectives of this study included: (1) to study the effects of MW-DA pretreatment variables (acid concentration, pressure, temperature, and time), integrated into combined severity factor on maximum FSE, (2) to apply BBD-RSM to quantify the effect of FSE, (3) to model using linear, quadratic, and ANN models, and (4) to analyze the uncertainty of BBD-based model by using MC simulations.
EXPERIMENTAL
Biomass Material and Constituents
The hazelnut shells were obtained from a local plant in Ordu, Turkey. Hazelnut shells were dried at 70 °C for 24 h and were milled through a 1-mm sieve. They were stored in plastic bags at room temperature. The composition of untreated hazelnut shells which was determined in previous study was cellulose (24.2 ± 1.0%), hemicellulose (28.2 ± 0.1%), total reducing sugar (679.2 ± 4.4 mg reducing sugar/g dry weight biomass), and lignin (47.2 ± 0.5%) (Uzuner et al. 2017).
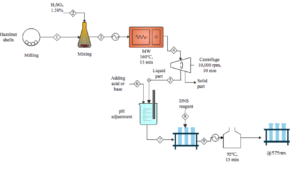
Microwave Pretreatment
The microwave acid digestion system (Biotage, Initiator RXF EU) was used as a microwave source. Pretreatment was carried out at three different levels: dilute acid concentration (X1; 0.5, 1.25, and 2.0%, w/w), pressure (X2; 5, 10, and 15 bar), temperature (X3; 120, 140, and 160 °C), and pretreatment time (X4; 5, 15, and 25 min) (Table 1). After pretreatment, the liquid was separated from solid residue by centrifugation. After centrifugation, hydrolysate samples were stored at +4 °C.
Conventional Thermochemical Pretreatment
Conventional thermochemical pretreatment was conducted in an autoclave under 130 °C for 31.7 min with H2SO4 having an acid concentration of 3.42% (Uzuner and Cekmecelioglu 2014). The same biomass loading and sample separation were performed for the following analysis.
Determination of Solid/Liquid Ratio
The solid/liquid ratio was defined as the ratio of the dry weight of hazelnut shells to the volume of sulfuric acid. Three different solid/liquid ratios as 1/20, 1/10, and 1/7 (w/v) were used as pretreatments of MW for the comparison of the resultant FSE.
Determination of Fermentable Sugar Content
Fermentable sugar extraction (FSE) in pretreated solids and enzyme hydrolysate were estimated using the 3,5-dinitrosalicylic acid (DNS) method (Miller 1959), as follows,
(1)
where DF denotes the dilution factor.
Severity Factor
Modeling was developed based on correlating the FSE during the MW assisted dilute acid pretreatment with severity factor. The severity factor, having been defined to relate temperature and time for steam explosion pretreatment, follows the first-order kinetics and obeys the Arrhenius equation by Overend and Chornet (1987). They defined a reaction ordinate (Ro, min) as follows,
(2)
where t is the residence time (min), Tr is the reaction temperature (°C), Tb is the base temperature (100 °C), and 14.75 is the conventional energy of activation assuming that the overall reaction is hydrolytic and the overall conversion is first order. The severity is equal to log (R0) during the steam explosion pretreatment. Chum et al. (1990) developed a modified severity factor for use in sulfuric acid pretreatment, as shown in Eq. 3,
(3)
where M0 is the modified severity factor, t is the residence time (min), C is the chemical concentration (wt%), Tr is the reaction temperature (°C), Tb is the base temperature (100 °C), and n is an arbitrary constant. This equation was adapted to be applied to the DA-MW pretreatment and for calculating the n-value.
Response Surface Methodology–BBD-Based Modeling
Statistical analyses were conducted to test the significant mean differences in MW-DA pretreatment in terms of FSE as a function of dilute acid concentration, pressure, temperature, and pretreatment time. Optimization was performed using the Box-Behnken Design (BBD) as the response surface methodology with a quadratic model. The BBD matrix was constructed by using four predictors with three levels. These included dilute acid concentration (DAC; 0.5, 1.25, and 2.0%, w/w), pressure (P; 5, 10 and 15 bar), temperature (T; 120, 140, and 160 °C), and pretreatment time (t; 5, 15, and 25 min) (Table 1). The levels of these variables were determined through preliminary experiments. The uncoded and coded predictors and the overall BBD are given in Table 1. FSE was reported by averaging three replicates of each run (a total of 15 runs). All the statistical analyses were performed by using JMP Pro 15.0.1. The following quadratic equation was used to fit the experimentally collected data,
Y=b0+b1X1+b2X2+b3X3+b4X4+b12X1X2+b13X1X3+b23X2X3+b14X1X4+b24X2X4+b11X12+b22X22+b33X32+b44X42 (4)
where Y is the response variable of FSE; bs are regression slope coefficients; and X1, X2, X3, and X4 are dilute acid concentration, pressure, temperature, and pretreatment time, respectively. Analysis of variance (ANOVA) and regression models were performed at a 95% confidence interval (p < 0.05) to define the significant terms of the predictive model. The MW-DA pretreatment was optimized by using the response optimizer function under DOE-RSM.
Further experimental runs were carried out in triplicate under the optimal conditions of FSE to validate the models. Variance analysis was performed to determine statistically significant effects of the four predictors (p < 0.05). Multiple comparisons were made by using Tukey’s test.
Data-driven Modeling
FSE was modeled in terms of acid concentration, pressure, temperature, and time. Multicollinearity was detected by using correlation matrices of Spearman’s rank-order and Pearson’s correlation. Regression models such as multiple linear regression (MLR) and multiple non-linear regression (MNLR) with stepwise regression, cubic model, and artificial neural networks (ANNs) were implemented and compared to one another.
A backpropagation (BP) neural model was generated for predicting the fermentable sugar extraction of hazelnut shells during the MW-DA pretreatment. Input variables considered were dilute acid concentration, pressure, temperature, and time, whereas the output variable included FSE. Input data were randomized into two sets: training (80%) and validation (20%). ANNs were developed by using JMP Pro 15.0.1 software. The ANN architecture consisted of an input layer with 4 neurons, an output layer with one neuron, and a hidden layer. One and two hidden layers with the number of neurons in these layers and transfer functions of hidden and output layers (Tansig and linear respectively) were performed for describing FSE to determine the optimal network topology.
To test and select the best-fit model, root mean square error (RMSE), coefficient of determination (R2), corrected Akaike’s Information Criteria (AICc) and K-Fold R-Square were used to evaluate the four models, as follows,
(5)
where n is the number of observations, k is the number of estimated parameters in the model, and SS is the sum of squares.
Multicollinearity among predictors was measured by using a variance inflation factor (VIF) and assumed to exit when VIF≥10. Autocorrelation was measured using the Durbin-Watson (DW) statistic and assumed to be positively correlated when DW=0, not correlated when DW=2, and negatively correlated when DW=4. Monte Carlo simulations were employed to determine the most influential predictors and parameter uncertainties in predicting the amount of FSE. Monte-Carlo simulation and global sensitivity analysis were also performed using JMP Pro 15.1.0. Optimal statistical distribution was identified for FSE from 16 alternative distributions (normal, normal with a Box-Cox transformation, normal with a Johnson transformation, lognormal, three parameter lognormal, exponential, two-parameter exponential, Weibull, three parameter Weibull, largest extreme value, smallest extreme value, gamma, three parameter gamma, logistic, loglogistic, and three parameter log-logistic). The smaller Anderson-Darling statistics and the greater p values showed the better distributions fit the experimental data. Tukey’s multiple comparison test following one-way analysis of variance (ANOVA) was performed to detect significant mean differences in FSE as a function of DAC, pressure, temperature, and time.
RESULTS AND DISCUSSION
Effects of Solid/Liquid Ratio on Fermentable Sugar Extraction
The samples were pretreated by using the solid/liquid ratios of 1:7 to 1:20 with a sulfuric acid concentration of 1.25% (w/w) to determine the effective solid/liquid ratio. Pretreatment processes were performed by using solid/liquid ratios of 1:7, 1:10, and 1:20 under the acid concentration of 1.25% (w/w) and the pressure of 5 bar at 160 °C for 15 min to obtain hydrolysates used for the FSE. FSE was estimated to be 23.95±0.46, 26.52±0.46, and 26.94±0.32% at the solid/liquid ratios of 1:20, 1:10, and 1:7, respectively. The solid/liquid ratios did not significantly affect the response of FSE (p > 0.05), therefore, the ratio of 1/20 was chosen as the best ratio for the FSE. Thus, the entire pretreatment experiments were performed by using the dilute acid at the solid/liquid ratio of 1:20.
Effect of the Relationship between the Microwave Assisted Dilute Acid Pretreatment Parameters on FSE
The fermentable sugars in the hydrolysate were measured and used to evaluate the overall pretreatment efficacy. Hazelnut shells used in this study contained 458.94 ± 4.39 mg reducing sugar/g dry weight biomass. The MW-DA pretreatment was performed to generate fermentable sugars, conversion efficiency, and severity parameter (Table 1).
The FSE from MW-DA pretreatment samples ranged from 16.7 to 291.2 mg/g. The highest FSE after the MW-DA pretreatment process was 291.2 mg/g pretreated biomass under 160 °C, 10 bar, 1.25% H2SO4, and 25 min, with the corresponding MW-DA pretreatment conversion efficiency of 63.45%. The amount of fermentable sugars increased approximately 10-fold with the temperature increase during the MW-DA pretreatment (Table 1, runs 1 & 10). Therefore, the temperature played the most crucial role in enhancing FSE, given the high F-values (78.18) and very low p-values (0.000) (Table 2) (p < 0.05).
The highest coefficients of correlation (r=0.58) were determined to be between temperature and FSE (data not shown). FSE after the MW-DA pretreatment process increased from 71.4 to 175.3 mg/g when dilute acid concentration was increased from 0.5 to 2.0% (Table 1, runs 18 & 21). When the time was increased from 5 to 25 min, FSE after the MW-DA pretreatment process increased from 143.4 to 243.6 mg/g (Table 1, runs 6 & 20). According to ANOVA results, significant linear terms were found for DAC (p=0.000), pressure (p=0.000), temperature (p=0.000), and time (p=0.000) with a positive effect on FSE (Table 2). Therefore, ANOVA results were also supported in this situation.
The conversion efficiency was also calculated as the ratio of the pretreated total amount of FSE to the initial amount of FSE. The conversion efficiency from the MW-DA pretreatment samples ranged from 3.64 to 63.45% (Table 1). The conversion efficiency increased with the temperature increase during the MW-DA pretreatment (Table 1, runs 13 & 14). However, the conversion efficiency decreased with the pressure increase during MW-DA pretreatment (Table 1, runs 9 & 12). Zhu et al. (2016) reported that MW-DA pretreatment of sugarcane bagasse resulted in a maximum sugar yield of 64% at 0.2 M H2SO4 at 170 °C for 7 min. Zhu et al. (2015) also reported that MW-assisted acid pretreatment of Miscanthus resulted in a maximum sugar yield of 73% at 0.2 M H2SO4 at 180 °C for 20 min. The differences in conversion efficiency values, when compared to the results of this study, were clearly due to raw material characteristics and processing conditions. Though the treatment conditions were somewhat different, and the temperature was much higher for hazelnut shells, the MW-DA pretreatment resulted in similar conversion efficiency (63.45%).
Table 1. (Un)coded Variables of Box-Behnken Design for DA-MW Pretreatment Process
The modified severity factors combine the effects of time, temperature, and acid concentration. The n-value for sulfuric acid pretreatment was found as 0.65. The severity factors under the different pretreatment conditions in this study are also tabulated in Table 1. Increasing the severity factor beyond the critical range decreases sugar recovery due to the denaturation of sugars and the formation of inhibitors such as furfural and HMF (Gonzales et al. 2016). The severity factors ranged from 1.35 to 3.23 (Table 1). When the severity factor was increased from 1.94 to 2.76, FSE increased from 53.47 to 62.08% (Table 1). The FSE conversion increased when severity was increased up to 3.23. The maximum conversion obtained was 63.45% at a severity factor value of 3.23 (Table 1). According to Pearson’s matrix results, the correlation between FSE and severity factors was determined as r=0.76 (data not shown). Fonseca et al. (2021) investigated the effects of dilute sulfuric acid assisted by microwave of sugarcane straw on fermentable sugars and concentration of inhibitors in hydrolysates. Fonseca et al. (2021) found the highest percentage of oligomeric sugars (62%) giving a low severity factor at 140 °C and 0.5% acid concentration.
Table 2. Revised Analysis of Variance (ANOVA) Results of Box-Behnken Design
For hazelnut shells, insignificant terms were excluded from the FSE models according to BBD variance (ANOVA) analysis results for MW-DA pretreatment conditions (Table 2). The FSE depends on the DAC, pressure, temperature, and time, and although their linear (p<0.05) effects created a positive impact on FSE, the quadratic effect (p<0.05) affected FSE negatively (Table 2). The R2 value of 0.82 and R2pred of 0.69 were found for the MW-DA pretreatment process (Table 2). The insignificant lack-of-fit value for FSE (p > 0.05) also showed that the model fit the experimental data well.
The response surface plots for FSE are plotted in Fig. 1 to provide a better visual understanding of variables. An increase in FSE was observed with the increasing pressure and dilute acid concentration at a constant temperature (140 °C) and time (15 min) (Fig. 1a). An increase in acid concentration from 0.5 to 1.25 % (w/w) provided the highest FSE of 228 mg/g at about 12 bars, but above 1.25 % (w/w) a decrease was observed. An increase was observed in FSE with an increase in temperature and time at a constant acid concentration (1.25 %, w/w), and pressure (10 bars) (Fig. 1b).
Fig. 1. Response surface plots for the effects of a) DAC and pressure b) temperature and time c) pressure and time d) pressure and temperature e) DAC and time f) temperature and DAC g) DAC and pressure on FSE
The highest temperature (160 °C) maximized the FSE (Fig. 1b), suggesting efficient cellulose decomposition under these conditions, and an increase in FSE was observed with an increase in temperature above 120 °C (Fig. 1b). This result agrees with Lacerda et al. (2015), who observed that an increase in temperature caused a decreasing amount of simple sugars due to the formation of inhibitors such as furfural and HMF. Fonseca et al. (2021) reported that the maximum recovery of sugars were found at 162 °C and 0.6 % (w/v) H2SO4. A linear increase in FSE was observed as time increased (Fig. 1b). The effect of pressure and time on FSE was shown in Fig. 1c, in which acid concentration and temperature were set at the center point. The FSE was observed to increase with a pressure up to 12 bars and to decrease slowly thereafter (Fig. 1c). The increased pressure and prolonged time affected the FSE, resulting in a decrease in fermentable sugar concentration due to monosaccharide degradation (Fig. 1c). It was observed from Fig. 1d that the lowest temperature (120 °C) minimized the FSE at the lowest pressure (5 bars). Loss of cellulose and hemicellulose occurs under elevated time and acid concentration thereby adversely affecting the FSE (Fig. 1e). A remarkable increase was observed in FSE as acid concentration and time increased, and this increase was limited beyond 1.5 % (w/w) (Fig. 1e). A similar positive effect of temperature was observed in Fig. 1f, indicating the effect of temperature and acid concentration on FSE, where 1.5% (w/w) acid concentration was the limit for this increase. An increase in FSE was observed with an increase in acid concentration (up to 1.5 %, w/w) and pressure (up to 12 bar) (Fig. 1g). The highest acid concentration minimized the FSE at the highest pressure (15 bar) due to sugar dehydration (Fig. 1g). This result agrees with Mikulski and Klosowski (2020), who also observed that sugar dehydration was highly dependent on pressure (54 to 152 psi).
ANN Modeling
A total number of 22 ANNs models were built and divided into four groups: (1) MLP with 3 to 9 neurons in one hidden layer at a learning rate of 0.1, (2) MLP with 3 to 9 neurons in one hidden layer at a learning rate of 0.01, (3) MLP with 3 to 6 in two hidden layers at a learning rate of 0.1, (4) MLP with 3 to 9 in two hidden layers at a learning rate of 0.01 (Table 3). The ANN model was run at various learning rates and in hidden layers to determine the power of the model. Different ANN topologies were summarized in Table 3. Table 3 shows that the 4-9-1 topology was the best with minimum RMSE and maximum R2 values. In the case of the training data set, R2 and RMSE values were 0.982 and 11.497, respectively, whereas for validating data set, R2 and RMSE values were 0.994 and 5.929, respectively (Table 3).
Table 3. Performance Indices of Various Approaches for Predicting Output Using ANN with Learning Rate 0.1
Comparison of BBD-Based Linear, Quadratic, Cubic, and ANN Models
The best fit BBD-based models of FSE through the MW-DA pretreatment process are presented in Table 4. The most important variable was the temperature for MLR, quadratic, and cubic models considering the magnitude of its coefficient. The degree of efficacy of varying MW-assisted dilute acid processes on the FSE can be deduced by comparing the magnitude of the coefficients of the second-order model (Table 4). The most important factor was the temperature with the highest coefficient (73.85), followed by acid concentration (44.12), pretreatment time (42.85), and pressure (32.60) (Table 4).
Table 4. Models for MW-DA Pretreatment Process Using BBD
The best-fit BBD-based quadratic models with the highest R2 and lowest RMSE and AICc were also run using randomly generated predictor values (n=100,000 and 54) simulated by Monte-Carlo in accordance with predictor distributions. FSE did not exhibit normal distribution due to low p value and high standard deviations (Fig. 2a). FSE exhibited normal with Johnson transformation (Fig. 2b). The best fit BBD based quadratic model was also run using randomly generated predictor values (n=100,000) simulated by Monte Carlo in accordance with predictor distributions (Fig. 2c). The standard deviations of FSE derived from the Monte Carlo simulation were also lower than those derived from the experimental data (Fig. 2c). Mean values of FSE derived from the experimental data (Fig. 2b) were in close agreement with those derived from the Monte Carlo simulations (Fig. 2c).
Suitable linear, quadratic, cubic, and ANN models for FSE as a function of acid concentration, pressure, temperature, and time were determined in terms of coefficient of determination (R2), AICc, and RMSE by JMP 15.0.1. The ANN model was chosen based on R2, AICc, and RMSE values for the response of FSE. R2, AICc, and RMSE were 0.99, 79.98, and 5.92 respectively for the ANN model (Table 5).
Fig. 2. Normal distributive function of FSE (mg/g) of DA-MW pretreatment process a) as a result of regression (n=54), b) as a result of Monte Carlo simulations (n=54), c) as a result of Monte Carlo simulations (n=100,000)
Table 5. Regression and ANN Models and Criterions
Optimization of DA-MW Pretreatment Process for Fermentable Sugar Extraction
Due to the complexity of the lignocellulosic material, it is hard to break all polysaccharide-lignin linkages to recover monomeric sugars (Lacerda et al. 2015). Therefore, the operating conditions of the MW-DA pretreatment process require optimization to achieve maximum sugar conversion. The operational settings were optimized to maximize FSE before enzymatic saccharification. The best solution for the best-fit model of ANN obtained for response optimization is shown in Fig. 3. The maximum FSE was achieved with 1.58% acid concentration, 8.5 bar, and 160 °C for 13 min (Fig. 3). The validation results (R2=0.99) for FSE at the optimal conditions indicated that the experimental FSE values were close to the BBD-derived ANN prediction. Also, a low value of the coefficient of variation (1.69 %) satisfies the adequacy of the model.
Fig. 3. Optimization plot showing optimum operational settings and predicted response value
Generally, the MW-DA pretreatment process has the potential to produce a high amount of fermentable sugar in a short period of time. It has been previously reported that MW has increased the reaction rate constants of reactions with high activation energies (Rodriguez et al. 2015). For comparison, conventional thermochemical pretreatment was conducted at 130 °C for 31 min with a 3% acid concentration to obtain maximum FSE (Uuzner and Cekmecelioglu 2014). Using a MW-DA pretreatment process, optimum FSE was obtained as 374 mg/g (81.4%) with 1.58% DAC, 8.5 bar, and 160 °C for 13 min. Maximum FSE conversion obtained from conventional thermochemical pretreatment was 62.8 % at 3.42% acid concentration and 130 °C for 31.7 min, which is lower than MW-DA pretreatment. In this study, the pretreatment time of the MW-DA pretreatment process was 2 times less. Thus, the MW-DA pretreatment process provided a high fermentable sugar yield with lower operating costs and treatment time than the traditional processes.
CONCLUSIONS
- In this study, the microwave dilute acid (MW-DA) pretreatment processing of hazelnut shells was compared to the conventional thermochemical process and optimized. The optimum conditions were found as 1.58% (w/w) acid concentration and 13 min at 8.5 bar and 160 °C which in turn revealed 81.4% conversion efficiency for FSE.
- High temperature, acid concentration, and pretreatment time were used in the traditional processes for the bioconversion of lignocellulosic biomass. However, the traditional pretreatment processes increase energy consumption, costs, and inhibitors to be able to provide high fermentable sugar yields.
- In this study, the MW-DA pretreatment process was observed to lower the costs significantly thanks to the decreases in pressure and acid requirement and pretreatment time. Thus, the MW-DA pretreatment process provided high fermentable sugar conversion with lower acid concentration and pretreatment time without enzymatic saccharification than the traditional processes.
ACKNOWLEDGMENTS
The author would like to thank Specialist Elif Ozturk at the Yildiz Technical University Science and Technology Application and Research Center, Istanbul, for assistance with microwave pretreatment analyses.
REFERENCES CITED
Atland, J. (2015). “Mulches for weed control in containers,” (http://oregonstate.edu/dept/nurseryweeds/feature_articles/mulch/mulch_for_containers.htm), Accessed February 13, 2015.
Chen, Y., Sharma-Shivappa, R. R., Keshwani, D., and Chen, C. (2007). “Potential of agricultural residues and hey for bioethanol production,” App. Biochem. Biotechnol. 142, 276-290. DOI: 10.1007/s12010-007-0026-3
Chum, H. L., Johnson, D. K., Black, S. K., and Overend, R. P. (1990). “Pretreatment catalyst effects and the combined severity parameter,” Appl. Biochem. Biotechnol. 24 (25), 1-14. DOI: 10.1007/BF02920229
Ethaib, S., Omar, R., Mazlina, M.K.S., Radiah, A.B.D., and Syafiie, S. (2016). “Microwave-assisted dilute acid pretreatment and enzymatic hydrolysis of sago palm bark,” BioResources 11(3), 5687-5702. DOI: 10.15376/biores.11.3.5687-5702
Fonseca, B. C., Reginatto, V., Lopez-Linares, J. C., Lucas, S., Garcia-Cubero, M. T., and Coca, M. (2021). “Ideal conditions of microwave-assisted acid pretreatment of sugarcane straw allow fermentative butyric acid production without detoxification step,” Bioresource Technol. 329, 124929. DOI: 10.1016/j.biortech.2021.124929
Gonzales, R. R. A., Sivagurunathan, P., Parthiban, A., and Kim, S-H. (2016). “Optimization of substrate concentration of dilute acid hydrolyzate of lignocellulosic biomass in batch hydrogen production,” Int. Biodeter. Biodegr. 113, 22-27. DOI: 10.1016/j.ibiod.2016.04.016
Hebda, T., Brzychczyk, B., Francik, S., and Pedryc, N. (2018). “Evaluation of suitability of hazelnut shell energy for production of biofuels,” Engineering for rural development, Conference paper. DOI:10.22616/ERDev2018.17.N437
Hendriks, A. T. W. M., and Zeeman, G. (2009). “Pretreatments to enhance the digestibility of lignocellulosic biomass,” Bioresource Technol. 100, 10-18. DOI: 10.1016/j.biortech.2008.05.027
Huang, J., Liu, Y., Sun, B., and Shang, Z. (2017). “Microwave assisted alkali extraction of bagasse hemicellulose enhanced by an enzymatic pretreatment process,” J. Bioresour. Bioprod. 2(3), 105-109. DOI: 10.21967/jbb.v2i3.117
Jang, M. O., and Choi, G. (2018). “Techno-economic analysis of butanol production from lignocellulosic biomass by concentrated acid pretreatment and hydrolysis plus continuous fermentation,” Biochem. Eng. J. 134, 30-43. DOI: 10.1016/j.bej.2018.03.002
Lacerda, V. S., Lopez-Sotelo, J. B., Correa-Guimaraes, A., Hernandez-Navarro, S., Sanchez-Bascones, M., Navas-Gracia, L. M., Martin-Ramos, P., Perez-Lebena, E., and Martin-Gil, J. (2015). “A kinetic study on microwave-assisted conversion of cellulose and lignocellulosic waste into hydroxymethylfurfural/furfural,” Bioresource Technol. 180, 88-96. DOI: 10.1016/j.biortech.2014.12.089
Li, H., Qu, Y., Yang, Y., Chang, S., and Xu, J. (2016). “Microwave irradiation- A green and efficient way to pretreat biomass,” Bioresource Technol. 199, 34-41. DOI: 10.1016/j.biortech.2015.08.099
Lu, X., Xi, B., Zhang, Y., and Angelidaki, I. (2011). “Microwave pretreatment of rape straw for bioethanol production: focus on energy efficiency,” Bioresource Technol. 102(17), 7937-7940. DOI: 10.1016/j.biortech.2011.06.065
Mesa, L., Martinez, Y., de Armas, A. C., and Gonzalez, E. (2020). “Ethanol production from sugarcane straw using different configurations of fermentation and techno-economical evaluation of the best schemes,” Renew. Energy 156, 377-388. DOI: 0.1016/j.renene.2020.04.091
Mikulski, D., and Klosowski, G. (2020). “Microwave-assisted dilute acid pretreatment in bioethanol production from wheat and rye stillages,” Biomass Bioenerg. 136, 105528. DOI: 10.1016/j.biombioe.2020.105528.
Miller, G. L. (1959). “Use of dinitrosalysilic acid reagent for determination of reducing sugar,” Anal. Chem. 31(3), 426-428. DOI: 10.1021/ac60147a030
Overend, R. P., and Chornet, E. (1987). “Fractionation of lignocellulosics by steam-aqueous pretreatments,” Philos. Trans. R. Soc. Lond. 321, 523-536. DOI: 10.1098/rsta.1987.0029
Ozcimen, D., and Ersoy-Mericboyu, A. (2010). “Characterization of biochar and bio-oil samples obtained from carbonization of various biomass materials,” Renew. Energ 35, 1319-1324. DOI: 10.1016/j.renene.2009.11.042
Rajeswari, G., Arutselvy, B., and Jacob, S. (2020). “Delignification of Aloe vera rind by mild acid associated microwave pretreatment to persuade enhanced enzymatic saccharification,” Waste Biomass Valor. 11, 5965-5975. DOI: 10.1007/s12649-019-00830-7
Rodriguez, A. M., Prieto, P., De la Hoz, A., Diaz-Ortiz, A., Martin, D. R., and Garcia, J. I. (2015). “Influence of polarity and activation energy in microwave-assisted organic synthesis (MAOS),” Chem. Open. 4, 308-317. DOI: 10.1002/open.201402123
Senol, H. (2019). “Biogas potential of hazelnut shells and hazelnut wastes in Giresun city,” Biotecnol. Rep. 24, e00361.DOI: 10.1016/j.btre.2019.e00361
Sombatpraiwan, S., Junyusen, T., Treeamnuk, T., and Junyusen, P. (2019). “Optimization of microwave-assisted alkali pretreatment of cassava rhizome for enhanced enzymatic hydrolysis glucose yield,” Food Energy Secur. 8 (4), 1-15. DOI: 10.1002/fes3.174
Uzuner, S., and Cekmecelioglu, D. (2014). “Hydrolysis of hazelnut shells as a carbon source for bioprocessing applications and fermentation,” Int. J. Food Eng. 10 (4), 799-808. DOI: 10.1515/ijfe-2014-0158
Uzuner, S., Sharma-Shivappa, R. R., and Cekmecelioglu, D. (2017). “Bioconversion of alkali pretreated hazelnut shells to fermentable sugars for generation of high value products,” Waste Biomass Valor. 8, 407-416. DOI:10.1007/s12649-016-9607-0.
Vintila, T., Sumalan, R., Popa, N. F., Dragomirescu, M., and Sala, F. (2019). “Microwave and steam mediated alkaline pretreatments of sweet sorghum bagasse: Study of the energy efficiency,” BioResources. 14(2), 4022-4034. DOI:10.15376/biores.14.2.4022-4034.
Xu, J., Cheng, J. J., Sharma-Shivappa, R. R., and Burns, J. C. (2010) “Lime pretreatment of switchgrass at mild temperatures for ethanol production,” Bioresource Technol. 101 (8), 2900-2903. DOI: 10.1016/j.biortech.2009.12.015
Yu, N., Tan, L., Sun, Z. Y., Tang, Y. Q., and Kida, K. (2018). “Production of bioethanol by integrating microwave assisted dilute sulfuric acid pretreated sugarcane bagasse slurry with molasses,” Appl. Biochem. Biotechnol. 185(1), 191-206. DOI: 10.1007/s12010-017-2651-9
Zhang, Z., Vancov, V., Mackintosh, S., Basu, B., Lali, A., Qian, G., Hopson, P., and Doherty, W. O. S. (2016). “Assessing dilute acid pretreatment of different lignocellulosic biomasses for enhanced sugar production,” Cellulose 23, 3771-3783. DOI: 10.1007/s10570-016-1043-6
Zhu, Z., Macquarrie, D. J., Simister, R., Gomez, L. D., and McQueen-Mason, S. J. (2015). “Microwave assisted chemical pretreatment of Miscanthus under different temperature regimes,” Sustain. Chem. Process 3(15), 2-13. DOI: 10.1186/s40508-015-0041-6
Zhu, Z., Rezende, C. A., Simister, R., McQueen-Mason, S. J., Macquarrie, D. J., Polikarpov, I., and Gomez, L. D. (2016). “Efficient sugar production from sugarcane bagasse by microwave assisted acid and alkali pretreatment,” Biomass Bioenerg. 93, 269-278. DOI: 10.1016/j.biombioe.2016.06.017
Article submitted: September 2, 2022; Peer review completed: October 1, 2022; Revised version received and accepted: November 14, 2022; Published: November 21, 2022.
DOI: 10.15376/biores.18.1.613-628
