Abstract
Heartwood color is a complex trait that affects the economic and aesthetic value of the wood but is highly variable. How the color of the heartwood varies spatially and temporally is poorly understood. To illustrate how heartwood color varies within a tree, two opposite aspects of wood within the same tree, representing differential growth rate, were used to model the long-short axis system jointly. The color of the heartwood on the long and the short axis was considered to be two different traits. By jointly modeling the long and short axes, the correlation was examined between aspect (spatial) and contemporaneous correlations (within aspect). Spatial and temporal correlations and their interactions describe the indirect physiological, genetic, and environmental changes in wood formation with time and position in the trunk. Spatial correlations were consistently lower than temporal correlations but were positive and significant. Between the heartwood color parameters, b* showed a relatively higher spatial correlation. The results suggest that there is a spatial correlation in the long-short axis for all color parameters and in the two surfaces. Variations between aspects were not statistically significant for any color parameter. The bivariate mixed model method revealed hidden physics behind heartwood color formation. Models need to be developed to account for both spatial and temporal dependence in studies of wood property change.
Download PDF
Full Article
Spatiotemporal Variation and Covariation of Heartwood Color in Planted Teak Wood from Ghana
Jerry Oppong Adutwum,a and Junji Matsumura b,*
Heartwood color is a complex trait that affects the economic and aesthetic value of the wood but is highly variable. How the color of the heartwood varies spatially and temporally is poorly understood. To illustrate how heartwood color varies within a tree, two opposite aspects of wood within the same tree, representing differential growth rate, were used to model the long-short axis system jointly. The color of the heartwood on the long and the short axis was considered to be two different traits. By jointly modeling the long and short axes, the correlation was examined between aspect (spatial) and contemporaneous correlations (within aspect). Spatial and temporal correlations and their interactions describe the indirect physiological, genetic, and environmental changes in wood formation with time and position in the trunk. Spatial correlations were consistently lower than temporal correlations but were positive and significant. Between the heartwood color parameters, b* showed a relatively higher spatial correlation. The results suggest that there is a spatial correlation in the long-short axis for all color parameters and in the two surfaces. Variations between aspects were not statistically significant for any color parameter. The bivariate mixed model method revealed hidden physics behind heartwood color formation. Models need to be developed to account for both spatial and temporal dependence in studies of wood property change.
DOI: 10.15376/biores.17.4.6178-6190
Keywords: Bivariate mixed models; CIE L*a*b*; Dependencies; Spatiotemporal process; Teak; Wood quality
Contact information: a. Graduate School of Bioresource and Bioenvironmental Sciences, Faculty of Agriculture, Kyushu University 744 Motooka, Nishi-Ku, Fukuoka 819-0395; b. Faculty of Agriculture, Kyushu University 744 Motooka, Nishi-ku, Fukuoka 819-0395;
* Corresponding author: matumura@agr.kyushu-u.ac.jp
GRAPHICAL ABSTRACT
INTRODUCTION
Wood formation in a tree occurs in a spatiotemporal sequence (Fayle 1973) involving the space element (radial or axial position in the tree) and the time element (age: beginning, yearly changes, and the end of wood formation). Wood layers increase in the quantity and quality around and along the tree stem, increasing variability and dependency over time. These two elements are integrated to form a shape/continuum by sharing some common functions e.g., physiology and genetics that create correlations during growth. These correlations, according to Fritts (1976) and Larson (1969), are physiological correlations and or genetic correlations (Savidge 2003). The correlation function between the spatial and temporal elements of tree growth determines the spatiotemporal structure of tree development. To gain insight into the growth process of the tree, an analysis of changes in wood properties evaluated across the wood core should be able to model changes in variance and covariance over time. The environment is the main cause of fluctuations in wood quantity and quality, as environmental conditions are not constant over time or space (Larson 1964; Burdon 1977; Bell and Lechowicz 1994).
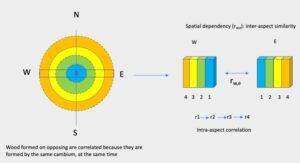
Trees exhibit an intriguingly complex plasticity in adapting to their environment because of their sessile fate (Larson 1964; Bell and Lechowicz 1994; Friml 2003). One of these plasticities is the differential wood production around and along the trunk known as eccentricity. Eccentric radial growth induces pronounced growth in one direction than in others occurring mostly in stems and branches. Trees correct imbalance mechanical loading induced by asymmetrical distribution of crown weight which may lead to differential tension stresses and differences in illumination (Williamson and Wiemann 2011). According to Cote and Day (1965), the longer-axis lignification occurs least or not at all in hardwoods. Eccentricity can be viewed as an inherent evolutionary mechanism of the tree’s response to environmental heterogeneity (Bell and Lechowicz 1994; Pruyn et al. 2000). A wood trait in eccentric stems may vary, although the cambium genotype is thought to be constant throughout the stem (Taylor 1968; Savidge 2003). The variations are the nature of gene expression in different physical and chemical environments to which the cambial cells are exposed (Pruyn et al. 2000; Savidge 2003). Eccentricity presents an interesting possibility to clarify the effect of environment on cambium genotype. Correlation between the two sides of the same tree can represent the extent to which a given trait shares the same genetic basis when measured in different aspects/environments (Via 1984, 1991). The effects of environmental variability on genetic covariation of traits are poorly understood in tropical tree species. The evolution of wood traits depends not only on the extent of variation of individual traits, but also on the pattern of covariation (Lande 1979; Lande and Arnold 1983). When trees are recognized as a space-time continuum, it is necessary to consider these sources of variation (Larson 1969).
Teak is a prime wood species in Ghana, reportedly planted on approximately 250,000 ha (FAO 2010; Apertorgbor and Roux 2015). It is valued for its texture and aesthetic traits, especially that of the heartwood. Heartwood in teak is believed to initiate at between 4 to 6 years (Moya et al. 2014) after the living functional cells die (Hillis 1987). Two main chemical constituents, namely tectoquinones and anthraquinines, in heartwood play an important role in the biological resistance of the wood (Rudman and Gay 1961; Sumthong et al. 2006; Lukmandaru and Takahashi 2009; Niamké et al. 2021; Gasparik et al. 2019). The spatial distribution of extractives in the tree could explain the variation in heartwood color (Niamké et al. 2021). Wood color, like any other trait, can vary widely within the tree. The drivers of these variations are known to be either spatial factor (position in the tree; height, radius), the growth rate of the tree, and the age of the tree (Rink 1987; Klumpers et al. 1993).
Little is known about the variation of heartwood color, the effect of spatial variation in environment on heartwood color, and its pattern of change. This is particularly an issue for teak grown in Ghana, where more research is needed. It is the purpose of this paper to describe such variations using mixed modeling techniques. A mixed bivariate model was developed for heartwood color variations representing two opposite sides of the same tree. The approach allows assessing the association between the two sides for a trait that can provide better insight into wood biology. Specific questions were: (1) Does spatial autocorrelation exist in eccentric heartwood color data? (2) How strong is the spatial autocorrelation? The authors believe that this approach is key to understanding heartwood color variation within-stem variation and would serve as a starting point to improve heartwood color uniformity, which is a fundamental requirement for suitable wood, particularly of planted trees. This study focuses on the correlation analysis between the two opposite sides of the same tree and its evolution over time. This approach may be able to capture both genetic and environmental factors affecting heartwood color variations.
EXPERIMENTAL
Sampling
All samples were collected from a private even-aged teak plantation with a spacing of 3 m × 3 m near Dormaa Ahenkro in the Bono region of Ghana. Three trees were selected at 18 years of age. 10 cm thick discs were prepared from each tree at 1.0 m intervals starting at 0.3 m above ground level until 5.3 m height level using a chainsaw. Two opposite sides of each tree were randomly selected from these discs. The selected sides were eccentric by a factor of at least 1.3. The two orthogonal radii represent the long and short axis of the tree at a given height. A radial strip (2 cm in the tangential direction and 3 cm thick in the longitudinal direction) was cut from each radius for analysis of the wood properties. The strips were air-dried at 20 °C and 65% relative humidity for several weeks to a dry-base moisture content of 12%.
Wood Color Measurement
The colorimeter used to evaluate the color of the wood was a Nippon Denshoku NR-3300 (Tokyo, Japan) with a measuring aperture diameter of 10 mm. The instrument was placed to record a sample representative of the strip surface from the pith outward at 1.0 cm intervals. A D56 standard illuminant and the 2o standard observer (daylight observation at 6500 K) parameters were also used. The color coordinates L*, a*, and b* were recorded. A total of 230 and 231 measurements were recorded for the cross-sectional (CS) and longitudinal-radial (LR) surfaces, respectively. Here, L* refers to lightness, a* refers to redness, and b* refers to yellowness. The color difference denoted as ∆E*, expressed as the distance between two points in the color coordinate system, was used to assess the uniformity of the color between the two opposite sides (aspects) and between the two surfaces. The equation for the total color difference ∆E* is given by Eq. 1 according to TAPPI (1994):
∆E* = (∆L*2 + ∆a*2 + ∆b*2)0.5 (1)
where ∆L is the difference in the lightness, ∆a is the difference in the a* coordinate, and ∆b is the difference in the b* coordinate
Statistical Analysis
The linear mixed-effects model
Heartwood color data represent a spatiotemporal repeated measurement on a tree. The properties on related trees and aspects are subject to correlations at any time due to shared genetic, physiological, and environmental effects. In addition, the wood properties of related trees at different points in time are also correlated due to the above factors. The long-short-axis data consists of two components representing spatial and temporal dependencies. By modelling the long-short axis data together, the dependency between the two aspects is accounted for in two ways: one for that between the aspects (i.e., purely spatial dependence) and the other for correlation within the long-short axis (i.e., purely temporal dependence). This modelling approach reveals the underlying process of heartwood color formation for the two aspects.
A general linear mixed model has the form (Laird and Ware 1982; Henderson 1984; Searle et al. 1992) as shown by Eq. 2:
y = Xβ + Zb + ε, (2)
b ~ N(0, G)
ε ~ N(0, R)
where y is the known vector of observations, β is a p x 1 vector of fixed effects with incidence matrix X, b is a q x 1 dimensional vector of random effects with corresponding design matrix Z, R is the variance-covariance matrix of errors and the random effects covariance matrix G. The expected value and variances are E[y] = Xβ, var[b] = G = and var[e] = R = for A the numerator relationship matrix and I an identity matrix.
Bivariate analysis
In the bivariate case, Eq. 2 was expanded to accommodate color trait values in the two aspects (stacking up the vectors), in such a way that β, b, and ε now contain the values for both radii (aspects).
(3)
The symbol is the Kronecker product). The distribution of the random effects and error terms is assumed to be normal with mean zero and variance-covariance matrix,
(4)
where and are the variances of the aspects 1 and 2, respectively, is the random treatment effects of covariance between aspects 1 and 2, and is the residual covariance between aspects 1 and 2. The nonzero covariances of random effects and error terms induce association between the responses. These represent the association of cambial evolution between the aspects and the evolution of cambial association over time, respectively.
Note that the two aspects are independent under joint normality if 
This implies there is no correlation at all between means of the trait in the two aspects.
The Pearson correlation ( between the two aspects were estimated using the standard formula from the long-short axis variances and covariance components as,