Abstract
Paper properties determine the product application potential and depend on the raw material, pulping conditions, and pulp refining. The aim of this study was to construct mathematical models that predict quantitative relations between the paper density and various mechanical and optical properties of the paper. A dataset of properties of paper handsheets produced with pulps of Acacia dealbata, Acacia melanoxylon, and Eucalyptus globulus beaten at 500, 2500, and 4500 revolutions was used. Unsupervised classification techniques were combined to assess the need to perform separated prediction models for each species, and multivariable regression techniques were used to establish such prediction models. It was possible to develop models with a high goodness of fit using paper density as the independent variable (or predictor) for all variables except tear index and zero-span tensile strength, both dry and wet.
Download PDF
Full Article
Using Apparent Density of Paper from Hardwood Kraft Pulps to Predict Sheet Properties, based on Unsupervised Classification and Multivariable Regression Techniques
Ofélia Anjos,a,b,* Esperanza García-Gonzalo,c António J. A. Santos,b,d Rogério Simões,d Javier Martínez-Torres,e Helena Pereira,b and Paulino J. García-Nieto c
Paper properties determine the product application potential and depend on the raw material, pulping conditions, and pulp refining. The aim of this study was to construct mathematical models that predict quantitative relations between the paper density and various mechanical and optical properties of the paper. A dataset of properties of paper handsheets produced with pulps of Acacia dealbata, Acacia melanoxylon, and Eucalyptus globulus beaten at 500, 2500, and 4500 revolutions was used. Unsupervised classification techniques were combined to assess the need to perform separated prediction models for each species, and multivariable regression techniques were used to establish such prediction models. It was possible to develop models with a high goodness of fit using paper density as the independent variable (or predictor) for all variables except tear index and zero-span tensile strength, both dry and wet.
Keywords: Unsupervised classification; Multivariable regression; Paper; Acacia dealbata; Acacia melanoxylon; Eucalyptus globulus
Contact information: a: Instituto Politécnico de Castelo Branco, Escola Superior Agrária, Apartado 119, 6001-909 Castelo Branco, Portugal; b: Centro de Estudos Florestais, Instituto Superior de Agronomia, Universidade de Lisboa, Tapada da Ajuda, 1349-017 Lisboa, Portugal; c: Facultad de Ciencias, Departamento de Matemática Aplicada, Universidad de Oviedo, 33005, Oviedo, Spain; d: Textile and Paper Materials Unit, Universidade da Beira Interior, 6201-001Covilhã, Portugal; e: Centro Universitario de la Defensa, Academia General Militar, 50090 Zaragoza, Spain;
* Corresponding author: ofelia@ipcb.pt
INTRODUCTION
Pulp fibers play the determining role in defining the strength properties of paper in both the dry and wet states. This is true for writing and printing papers, which commonly contain 75% to 80% pulp fibers, 20% to 25% inorganic materials, and small amounts of functional additives, as well as for tissue papers, which are primarily pulp fibers. The performance of the different types of papers depends mostly on the properties of the pulp fibers, which are determined by the pulping and bleaching conditions and the properties of the initial pulping raw material.
Paper’s properties (e.g., density, mechanical strength, and optical and surface properties) are directly related to its suitability for use in various applications. Among these, strength properties are very important because they determine the paper’s resistance to stresses and performance in printing; for example, tensile strength can be used as one potential indicator of the resistance to web breaks during printing or converting.
The density of the paper sheet is another important parameter that influences many other properties, although it also depends on the raw material fiber structure, the cooking process, and the pulp refining level (Santos et al. 2008a,b; Paavilainen 1993a,b). Seth and Kingsland (1990) showed that the tensile strength increased with increasing paper density and decreased with decreasing fiber strength. Paavilainen (1993a,b) reported an increase in tensile strength as a consequence of the increase in paper density, as well as of good bonding ability and high intrinsic fiber strength. The relationship between density and various paper properties has been examined for some species (Anjos et al. 2014; Santos et al. 2012; Amidon 1981).
It would be interesting to predict different paper properties using a few, or only one, predictor variables. This was the focus of this work: statistical tools were applied to predict paper properties using paper density as the predictor variable for hardwood pulps of Acacia dealbata, Acacia melanoxylon and Eucalyptus globulus. The aim was to develop mathematical models of the correlation between the paper density of some hardwood species and the various mechanical and optical properties of the resulting paper.
Because different species were considered, unsupervised classification techniques were used to assess the need to perform separate prediction models for each species. Specifically, an analysis of the data set (with all species and properties) was made using principal component analysis (PCA). To establish predictive models, multivariate regression techniques were applied, and the models were kept as simple as possible, incorporating only those predictor variables with greater explanatory power. The ultimate goal was to obtain straightforward prediction models that closely adhere to the data available and that could be valid when applied to independent data predictions.
EXPERIMENTAL
Data
Data concerning various paper properties from three hardwood species (A. dealbata, A. melanoxylon, and E. globulus) at three refining levels from a previous study (Santos et al. 2006, 2005) were used.
The wood chip samples of each species (1000 g o.d.) were submitted to a conventional kraft cooking process in a forced circulation digester under the following reaction conditions: effective alkali charge, 22% (as NaOH); sulfidity index, 30%; liquor/wood ratio, 4/1; time to temperature, 90 min; and time at temperature (160 °C), 120 min. The cooked chips were disintegrated, washed, and screened on an L&W screen with a 0.3-mm slot width. The cooked pulps were bleached with a D0E1D1E2D2 bleaching sequence, using a kappa factor of 0.2 in the D0 stage. The ClO2 charges were 1.6 % in D1 and 0.6 % in D2 for all pulps; the extraction (E) was made with 1.3 and 0.5 % of NaOH respectively for E1 and E2.
The bleached pulps were beaten in a PFI mill at 500, 2500, and 4500 revolutions under a refining intensity of 3.33 N/mm, according to ISO 5264-2 (2011).
Paper handsheets were prepared according to standards (TAPPI T205 om-88 (1988); NP EN 20187, ISO 187 (1990)) and tested for their structural, mechanical, and optical properties, as follows: 1) density (Dens) according to TAPPI T220 sp-01 (2001); 2) resistance of air permeability (Perm) measured in a Gurley® apparatus according to TAPPI T460 om-96 (1996); 3) Bekk smoothness (Smoo) measured with a Bekk® Tester from Messmer according to TAPPI T479 cm-09 (2009); 4) tensile index (Tens) in a Adamel Lhomargy DY 20 testing machine with a 1.0-kN load cell according to ISO 1924-2 (1994). The distance between clamping jaws was 100 mm, and the crosshead speed was 10 mm/min; 5) stretch (Stre) is the elongation before rupture measured during tensile strength testing, expressed as the percentage of the initial length; 6) burst index (Burs) determined with Burst-O-Matic® equipment from Messmer according to TAPPI T403 om-10 (2010); 7) tear index (Tear) was determined with an Elmendorf ® tearing test from Adamel Lhomargy ED 20 according to TAPPI T220 sp-96 (1996); 8) zero-span tensile strength was determined in dry (Zssd) and wet (Zssw) handsheet samples, with a PULMAC® Inst., model TS-100, according to TAPPI T273 pm-95 (1995); 9) opacity (Opac), brightness (Brig), and light scattering coefficient (Ligh) were determined with a spectrophotometer Touch 2 Technidyne (mod. ISO) according to ISO 2469 (2007), ISO 2470 (2008), and ISO 2471 (2008), respectively; and (F) brightness was determined at 457 mm. These properties were selected to characterize the performance of the different fiber raw materials and in accordance to their relevance for paper characterization.
The dataset of the physical properties analyzed in ten handsheets of each species is summarized in Table 1.
Table 1. Physical Properties of the Handsheets for the Three Species
Data Processing
The convenience of grouping the different species for quantitative study was studied by PCA of the paper handsheet properties. The principal component transformation is a commonly used linear transformation that finds a new set of orthogonal, uncorrelated variables and their corresponding axes such that their origin is at the data mean. In these new axes, the data variance is explained in decreasing order.
The least squared method was used to fit the data with the different models, choosing models as simple as possible that attained good fitness (i.e., if a simple model achieved good fitness, it was accepted; if not, more complicated models were studied). The parameters used to measure the goodness of fit were the coefficient of determination, R2, and the root mean squared error, RMSE.
R2 indicates the proportion of total variation in the dependent variable that is not explained by the model. A dataset contains values ti, each of which has an associated modelled value yi. The former are called the observed values and the latter are often referred to as the predicted values. Variability in the dataset is measured through different sums of squares: SStot, the total sum of squares, proportional to the sample variance and SSerr, the residual sum of squares.
The coefficient of determination is given by,
(1)
A coefficient of determination of 1.0 indicates that the regression curve fits the data perfectly. The root mean squared error, RMSE, is the sample standard deviation between observed and predicted values, defined as,
(2)
While R2 is scale-independent, RMSE is not and is only valid to compare the errors of different models for the same variable.
As a preparatory step in PCA, the data were normalized by subtracting the mean and dividing by the standard deviation. The samples were labeled AD (A. dealbata), AM (A. melanoxylon), and EG (E. globulus), and the refining levels were denoted R1 (PFI 0 rev), R2 (PFI 500 rev), R3 (PFI 2500 rev), and R4 (PFI 4500 rev).
The generation process model has an inherent testing process with 90% and 10% of the data for optimal selection of parameters that may be considered a validation process. A following independent validation process was not performed due to insufficient data
RESULTS AND DISCUSSION
Principal Component Analysis
The PCA results of all measured paper properties, as shown in Fig. 1, grouped the properties by species and by refining level. The two principal components explained 88% of the total variability. The first component and the main factor was the refining level, explaining 70%; this seems to be a reflection of the importance of the refining into the fiber structure with determining effects in many of the properties related to the fiber and inter-fiber bonding.
Fig. 1. Principal component analysis for the normalized data of AD (A. dealbata), AM (A. melanoxylon), and EG (E. globulus) for the four refining levels R1 (PFI 0 rev), R2 (PFI 500 rev), R3 (PFI 2500 rev), and R4 (PFI 4500 rev)
The second principal component was the wood species and seems to be a reflection of the significant fiber differences between the species; therefore the species should be analyzed separately. Moreover, higher differences were observed when comparing both the Acacia species and the Eucalyptus species, in agreement with previous results (Santos et al. 2006).
This difference resulted from the differences between the fiber characteristics and morphology, as explained by Anjos et al. (2011) for A. melanoxylon and Santos et al. (2008a) for E. globulus. The fiber length, width, and especially wall thickness determine its flexibility and collapsibility, which in turn determine the structure, optical, and mechanical properties of the paper. More flexible, collapsible fibers yield more densified paper handsheets (Paavilainen 1993b).
The decision was therefore made to develop predictive models of the paper properties by multivariate regression techniques separately for each species.
The refining level strongly affected the physical properties of the handsheets, represented by the first principal component; thus, the independent variables in the predictive models were highly correlated with the refining level. Refining improved internal and external fibrillation, enhancing fiber flexibility, collapsibility, and fiber-fiber bonds (Fardim and Duran 2003). These effects increased the density of paper handsheets; decreased opacity, light scattering, bulk, and bending stiffness; and increased tensile strength and burst resistance. Tear resistance increased initially with beating but may have decreased thereafter. The extent and intensity of these behaviors were species-dependent and depended on the pulp fiber characteristics (Paavilainen 1993b; Santos et al. 2008a; Anjos et al. 2011).
The PCA of the paper properties, considering the three species and the four refining levels (Fig. 2.), shows that the first component explained 69% of the total variability and the second component explained 17%. There were three groups along the first component: 1) density, tensile index, stretch, burst index, Bekk smoothness, and resistance to air permeability; 2) tear index, zero-span dry, and zero-span wet; and 3) light scattering coefficient, brightness, and opacity. Groups 1 and 3 were separated primarily by the first principal component, while the second principal component separated group 2 from the others.
Fig. 2. Principal component analysis of the normalized data of paper properties for the three species and four refining levels.
These results suggest that the variables included in groups 1 and 3 were fairly correlated with each other, while the variables in group 2 were not correlated with the rest of the properties. This was expected because the tear index and zero-span tensile strength depend on the intrinsic fiber resistance (Andersson 1981).
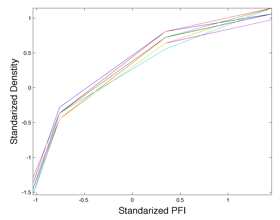
The refining level (PFI) strongly conditions the paper properties. For instance, Fig. 3 shows how the density increased as the PFI revolutions increased for A. dealbata. A similar relationship between density and PFI was observed for A. melanoxylon and E. globulus.
Fig. 3. Standardized density vs. standardized PFI revolutions for A. dealbata.
These results support the decision to separately develop the predictive models of the mechanical properties obtained by multivariate regression techniques for each species.
Multivariable Regression Models
The partial correlation coefficients between the different properties are shown in Tables 2, 3, and 4 for the three different species.
Table 2. Matrix of Partial Correlation Coefficients between Variables for A. dealbata
Density correlated well with all properties except tear index and zero-span tensile strength, both dry and wet. This property was grouped together (group 2) in the PCA, with the first principal component close to zero and positive values for the second principal component. The correlation with resistance to air permeability was intermediate (this property had the lowest value for the second principal component).
Table 3. Matrix of Partial Correlation Coefficients between Variables for A. melanoxylon
Table 4. Matrix of Partial Correlation Coefficients between Variables for E. globulus
To obtain simple prediction models, only the predictor variables with the highest explanatory power were incorporated. The density was used as the independent (or predictor) variable. As seen in Fig. 3, density was directly related to PFI, i.e., Density = f(PFI), which strongly affected the other properties. Additional independent variables were incorporated only when the goodness of fit was poor.
The prediction model can be performed with a linear function (2 parameters), polynomial of order 2 (3 parameters), a Gaussian function (3 parameters), or a power function (2 parameters), each with density as only predictor variable. The R2 coefficient was quite high in all cases except for the dry and wet zero-span tensile strengths and tear index variables in some cases (Tables 5, 6, and 7).
Models for the tensile index as a function were very accurate, with R2coefficients of 0.90, 0.91, and 0.98 for A. dealbata, A. melanoxylon, and E. globulus, respectively. This relationship is well known (Vainio and Paulapuro 2007), but no models have been proposed. It is also well known that increasing the paper density strongly improves the paper strength (Santos et al. 2006; Anjos et al. 2011; Santos et al. 2012; Zeng et al. 2013), which is mostly due to increased fiber-fiber contact. There is a strong inverse relationship between the density and the light scattering coefficient (Batchelor and He 2005; Hubbe et al. 2008).
Table 5. Fitted Models for the Different Variables for A. dealbatawith their Corresponding Measures of Goodness of Fit, R2, and RMSE
Graphical examples of these models are presented in Figs. 4 and 5. As shown in Fig. 4, the dependent variable was the wet zero-span tensile strength, and the independent variables were density and Bekk smoothness for A. dealbata; in this case, the goodness of fit was improved by adding this additional variable. Figure 5 depicts a linear fit for A. melanoxylon in which the burst index depended on the density.
Fig. 4. Fitted surface for wet zero-span tensile strength determined as the dependent variable and density = f(PFI) and Bekk smoothness as the independent variables for the A. dealbata
Table 6. Fitted Models for the Different Variables for A. melanoxylonwith their Corresponding Measures of Goodness of Fit, R2, and RMSE
Fig. 5. Fitted curve for burst index as the dependent variable and density = f(PFI) as the independent variable for A. melanoxylon
Table 7. Fitted Models for the Different Variables for E. globulus with their Corresponding Measures of Goodness of Fit, R2, and RMSE
CONCLUSIONS
- It was possible to use unsupervised classification techniques to assess separate prediction models of paper properties for each of the hardwood species studied and multivariable regression techniques to establish the prediction models.
- The PCA of the paper handsheets showed that different species should be analyzed separately and that the pulp refining level strongly conditioned the physical properties; thus, predictor variables were highly correlated with the refining level.
- The predictor variable density had the highest explanatory power but depended on the refining level, whose value strongly affected the values of other properties.
- All variables except for tear index and zero-span tensile strength, both dry and wet, could be predicted using density-based models with high goodness of fit.
ACKNOWLEDGMENTS
Centro de Estudos Florestais is a research unit funded byFundação para a Ciência e a Tecnologia (Portugal) within UID/AGR/00239/2013. The research unit Fiber Materials and Environmental Technologies is funded by Fundação para a Ciência e a Tecnologia (Portugal) within UID/Multi/00195/2013.
REFERENCES CITED
Amidon, T. (1981). “Effect of wood properties of hardwood on kraft paper properties,” TAPPI J. 64(3), 123-126.
Andersson, M. (1981). “Aspects of z-strength in pulp characterization,” Svensk Papperstidn. 84(6), R34-R42.
Anjos, O., Santos, A., and Simões, R. (2011). “Effect of Acacia melanoxylon fibre morphology on papermaking potential,” Appita J.64(2), 185-191.
Anjos, O., Santos, A., Simões, R., and Pereira, H. (2014). “Morphological, mechanical and optical properties of cypress,” Holzforschung 68(8), 861-995. DOI: 10.1515/hf-2013-0125.
Batchelor, W., and He, J. (2005). “A new method for determination the relative bonded area,” TAPPI J. 4(6), 23-38.
Fardim, P., and Duran, N. (2003). “Modification of fiber surface during pulping and refining as analyzed by SEM, XPS and ToF-SIMS,” J. Colloid. Surf. 223(2), 263-276. DOI: 10.1016/S0927-7757(03)00149-3.
Hubbe, M. A., Pawlak, J. J., and Koukoulas, A. A. (2008). “Paper’s appearance: A review,” BioResources 3(2), 627-665. DOI: 10.15376/biores.3.2.627-665
ISO 1924-2 (1994). “Paper and board, Determination of tensile properties, Part 2: Constant rate of elongation method,” International Organization for Standardization, Geneva, Switzerland.
ISO 2469 (2007). “Measurement of diffuse radiance (reflectance) factor,” International Organization for Standardization, Geneva, Switzerland.
ISO 2470 (2008). “Measurement of diffuse blue reflectance factor (ISO brightness),” International Organization for Standardization, Geneva, Switzerland.
ISO 2471 (2008). “Determination of opacity (paper packing) – diffuse reflectance method,” International Organization for Standardization, Geneva, Switzerland.
ISO 5264-2 (2011). “Pulps, Laboratory beating, Part 2: PFI mill method,” International Organization for Standardization, Geneva, Switzerland.
NP EN 20187, ISO 187 (1990). “Paper, board and pulps. Standard atmosphere for conditioning and testing and procedure for monitoring the atmosphere and conditioning of samples,” International Organization for Standardization, Geneva, Switzerland.
Paavilainen, L. (1993a). “Importance of cross-dimensional fibre properties and coarseness for the characterisation of softwood sulphate pulp,” Paperi ja Puu 75(5), 343-351.
Paavilainen, L. (1993b). “Conformability, flexibility and collapsibility of sulphate pulp fibers,” Paperi ja Puu 75(9-10), 689-702.
Santos, A., Amaral, M., Vaz, A., Anjos, O., and Simões, R. (2008a). “Effect of Eucalyptus globulus wood density on papermaking potential,” TAPPI J. 7(5), 25-32.
Santos, A., Anjos, O., Amaral, M., Gil, N., Pereira, H., and Simões, R. (2012). “Influence on pulping yield and pulp properties of wood density of Acacia melanoxylon,” J. Wood Sci. 58(6), 479-486. DOI: 10.1007/s10086-012-1286-2.
Santos, A., Anjos, O., and Simões, R. (2006). “Papermaking potential of Acacia dealbata and Acacia melanoxylon,” Appita J. 59(1), 58-64.
Santos, A., Anjos, O., Simões, R. (2005). “Avaliação da qualidade do papel produzido com fibra de Acacia spp.,” Silva Lus. 13(2), 249-266.
Santos, A., Anjos, O., Simões, R. (2008b). “Influence of kraft cooking conditions on the pulp quality of Eucalyptus globulus,” Appita J. 61(2), 148-155.
Seth, R., and Kingsland, M. (1990). “The reinforcing properties of softwood kraft pulps,” Pulp Pap.-Canada 91(7), 68-72, 74-75.
TAPPI T205 om-88 (1988). “Forming handsheets for physical tests of pulp,” TAPPI Press, Atlanta, GA.
TAPPI T220 sp-96 (1996). “Physical testing of pulp handsheets,” TAPPI Press, Atlanta.
TAPPI T220 sp-01 (2001). “Physical testing of pulp handsheets,” TAPPI Press, Atlanta.
TAPPI T273 pm-95 (1995). “Wet zero-span tensile strength of pulp, test method,” TAPPI Press, Atlanta, GA.
TAPPI T403 om-10 (2010). “Bursting strength of paper,” TAPPI Press, Atlanta, GA.
TAPPI T460 om-96 (1996). “Air resistance of paper (Gurley method),” TAPPI Press, Atlanta, GA.
TAPPI T479 cm-09 (2009). “Smoothness of paper (Bekk Method),” TAPPI Press, Atlanta, GA.
Vainio, A., and Paulapuro, H. (2007). “Interfiber bonding and fiber segment activation in paper,” BioResources 2(3), 442-458. DOI: 10.15376/biores.2.3.442-458
Zeng, X., Vishtal, A., Retulainen, E., Sivonen, E., and Fu, S. (2013). “The elongation potential of paper. How should fibres be deformed to make paper extensible?,” BioResources 8(1), 472-486. DOI: 10.15376/biores.8.1.472-486
Article submitted: April 27, 2015; Peer review completed: July 5, 2015; Revised version received and accepted: July 14, 2015; Published: July 30, 2015.
DOI: 10.15376/biores.10.3.5920-5931