Vacuum-assisted water removal from highly refined furnishes

Abstract

A vacuum-assisted sheet former was used for analyzing water removal from refined bleached hardwood kraft pulp furnishes. The Schopper Riegler (SR) values of the studied furnishes ranged from 43 to 97. Water removal time increased significantly with increasing SR value; the water removal time for SR97 furnish was two orders of magnitude longer than for SR43. Retention behaved differently with different SR levels. Retention was approximately constant for SR43 and SR72, for SR85 retention was initially slightly lower, and for SR97 retention was initially very low. The clogging of the wire due to the fines was very strong for SR97. A simple model of flow resistance of the filtered sheet worked very well for SR43 and SR72, and the model worked reasonably well for SR85. However, for higher SR levels, a retention model is needed to predict accurately the water removal in real-life applications.

Full Article

Vacuum-assisted Water Removal from Highly Refined Furnishes

Antti Koponen,^a,* Juan Cecchini,^b Samuli Heiskanen,^b Merja Selenius,^a and Ari Jäsberg ^a

A vacuum-assisted sheet former was used for analyzing water removal from refined bleached hardwood kraft pulp furnishes. The Schopper Riegler (SR) values of the studied furnishes ranged from 43 to 97. Water removal time increased significantly with increasing SR value; the water removal time for SR97 furnish was two orders of magnitude longer than for SR43. Retention behaved differently with different SR levels. Retention was approximately constant for SR43 and SR72, for SR85 retention was initially slightly lower, and for SR97 retention was initially very low. The clogging of the wire due to the fines was very strong for SR97. A simple model of flow resistance of the filtered sheet worked very well for SR43 and SR72, and the model worked reasonably well for SR85. However, for higher SR levels, a retention model is needed to predict accurately the water removal in real-life applications.

DOI: 10.15376/biores.18.1.1398-1419

Keywords: Forming; Furnish; Highly refined; Water removal; Vacuum; Sheet former

Contact information: a: VTT Technical Research Centre of Finland Ltd, Koivurannantie 1, 40400 Jyväskylä, Finland; b: Valmet Technologies, Inc., Rautpohjankatu 3, 40700 Jyväskylä, Finland;

* Corresponding author: Antti.Koponen@vtt.fi

GRAPHICAL ABSTRACT

INTRODUCTION

Micro or nanofibrillated celluloses (MFC or NFC) have been studied as additives in paper making. The composite papers produced by such addition have many beneficial properties and possible applications. For example, they have improved barrier, strength, surface, and optical properties (Lavoine et al. 2012; Balea et al. 2020; Das et al. 2020). However, the addition of MFC/NFC leads to a significant reduction in the rate of dewatering due to the sealing of the fiber web. The small fibrils contained in MFC/NFC are very effective at sealing the web due to their large surface area, high aspect ratio, and high hydrophilicity (Rantanen et al. 2015; Sjöstrand et al. 2019; Balea et al. 2020).

One way to produce furnishes containing MFC is by extensive refining using a conventional refiner (Chen et al. 2016; Nechyporchuk et al. 2016; Shafei-Sabet et al. 2016; Hubbe et al. 2017). This method has the advantage that it is a developed technology, and industrial-scale equipment already exists. However, this method does not produce a homogeneous suspension of MFC but a mixture of fibrillated fibers and fines; both are generated at the same time in the refining process. Fibrillation is generated from the secondary fiber wall, and fines are produced by primary wall removal and fiber cutting (Tripattharanan 2003). Thus, the produced furnishes suffer from web sealing due to the large proportion of fines (Hubbe 2002; Chen et al. 2009) in addition to the fibrils. However, the produced fines may also lead to increases in strength and other mechanical properties (Lindqvist et al. 2012; Fischer et al. 2017).

These highly refined fibers could be applied in various ways. For example, it has been suggested that fines could be used in many applications where the use of MFC is currently being evaluated (Fischer et al. 2017). An alternative interesting approach would be to utilize highly refined fibers directly for novel cellulose-based applications. The tethered MFC produced by the refining can lead to equivalent strength properties as MFC composites, but with considerable drainage benefits (Su et al. 2013). Highly refined fibers could be used together with MFC as paper composites leading to a combination of tethered and free MFC.

The main challenge for applications is the difficult dewatering of these furnishes. This is big a challenge, as the dewatering of the wet fiber web requires more energy than any other part of the paper manufacturing process. On a conventional paper machine, water is removed in three consecutive sections, which are the forming, pressing, and drying sections. The cheapest section to remove a unit of water is by far the forming section, where water is removed from the web by gravity, shear, and vacuum dewatering. Thus, considering possible applications it is important to understand the factors affecting the dewatering at the forming section so that water removal there can be maximized, and overall costs minimized. This is especially the case for highly refined furnishes or furnishes containing a large amount of MFC, which are difficult to dewater especially at the forming section where the included fibrils and fines lead to web sealing as described above.

Due to its importance, the dewatering process has been widely studied (Hubbe and Heitmann 2007; Ramaswamy 2003; Kalliokoski 2011; Hubbe et al. 2020). Recent research has focused on the dewatering of composite furnishes containing MFC or NFC (Rantanen et al. 2015; Sjöstrand et al. 2019; Ahadian et al. 2022). However, not much focus has been put on the dewatering of highly refined fibers, which, as described above, could be used as a substitute for MFC or in combination with it. Understanding the dewatering process of such furnishes is useful as the equipment needed for their application already exists on an industrial scale since conventional refiners and paper machines can be utilized.

This paper examines the dewatering process for highly refined furnishes at different refining levels. The goal is to understand the parameters affecting the dewatering rate and to identify the operating window on a pilot or production machine for such furnishes. The Schopper-Riegler (SR) values of the studied furnishes range from 43 to 97. Notice that SR97 is so high that it is, e.g., clearly outside the range of the AFT freeness conversion chart (AFT 2018), which ends at SR80. When identifying the operating window, certain limitations need to be taken into consideration. A pilot or production machine is limited to certain vacuum levels. Initially, the vacuum level must be kept very low to help minimize the air permeance, and the maximum vacuum level at the end of the former is tens of kPa. The dewatering time is also limited, since the former length is set, and the machine speed must be high enough for a profitable process.

In this article, the effects of the refining level (SR43, SR72, SR85, and SR97) on the dynamics of the dewatering process are investigated. First, the sheet former setup used for the dewatering measurements is described. Next, the effects of the refining level, basis weight, and vacuum level on the retention and the dewatering time are discussed. Then, the effect of these parameters on the time evolution of the water column height and the resistivity of the fiber web is analyzed. Finally, a linear resistivity model is applied to the resistivity data; the model is found to work reasonably well up to SR85.

EXPERIMENTAL

Materials

Furnishes

Three BHKP (eucalyptus) furnishes were made at the refining levels of SR43, SR85, and SR97. Moreover, SR72 furnish was made by mixing SR43 and SR85 furnishes at mass fractions of 60% and 40%, respectively. Furnish light microscopy images are shown in Fig. 1. In addition to increasing the fines content, increasing SR level led to higher fiber fibrillation and shorter fiber length. The furnish properties are shown in Table 1. The Schopper Riegler (SR) values were determined according to the ISO 5267-1 (2000) standard. The conversions between the CSF and SR values were performed using the AFT freeness conversion chart (AFT 2018). SR97 was clearly outside the freeness range presented in this chart. The fines content was determined using an L&W fiber tester plus (ABB AB/Lorentzen & Wettre, Kista, Sweden). Water retention value (WRV) was measured according to the ISO23714 (2014) standard. For SR97, the WRV could not be measured with this method, but it is likely between 3 and 4 (Ahadian et al. 2022). (In the ISO23714 (2014) standard, the suspension is put in a small cup that has a metal wire at its bottom. Then, a mild vacuum is made below the wire with a Büchner funnel. Next, the cup is placed in a centrifuge to continue the water removal. With SR97 the wire was blocked by the fines almost immediately and most of the water stayed in the suspension.)

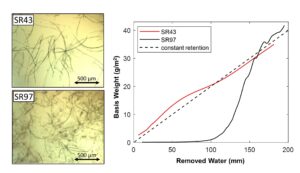
Fig. 1. Light microscopy images of a) SR43, b) SR72, c) SR85, d) SR97

Table 1. The Properties of the Furnishes

Vacuum-assisted sheet former

The forming studies were performed with a vacuum-assisted sheet former (Lehmonen et al. 2020). This forming device (Fig. 2) has a larger sheet size (210 mm × 300 mm) and enables higher vacuum levels when compared to conventional sheet formers. Water removal can be performed with the device with vacuum levels between 5 and 70 kPa. Vacuum levels are thus comparable with those used in real paper machine forming sections. Valmet Forming Fabric GM (thread count 108 to 140) was used as the wire mesh.

Fig. 2. a) Schematic of the vacuum-assisted sheet former. b) The pulp chamber during mixing of the furnish by injected air. c) The wet sheet on the wire after forming.

At the beginning of processing, the water inlet valve was opened. The valve was kept open until the 10-L underside of the mold was full of process water and the acrylic mold was filled up to the level of 50 mm. The fibers were added as a fiber suspension to the mold, and the mold was filled with process water up to 200 mm level. Finally, before forming, the suspension was mixed by injecting air from below the wire (Fig. 2b).

During forming, a wet sheet was formed on the wire (Fig. 2c). At the end of the process, after the water column above the sheet had vanished, air flowed through the sheet a few seconds, and the solid content of the final sheet was of the order of 10%. After forming, the sample was collected for determination of retention. The sheet could also be pressed and dried for further analysis. In addition to the time evolution of vacuum, P(t), measured below the wire (Fig. 3a), the time evolution of the position of the fiber suspension surface, h(t), was measured with an ultra-sonic detector (Fig. 3b). Figure 3a shows that pressure under the wire reached its maximum value, P_max, 0.2 s after the valve had been opened (at t = t_P). The vacuum initially slightly overshot and oscillated before reaching a constant value. These tests reflect water removal dynamics taking place in a forming section before the waterline, after which air starts flowing through the filtered sheet.

In this study, the forming consistency ranged between 0.015 and 0.03% depending on the target basis weight and the furnish retention. Vacuum levels varied between 5 and 42 kPa. The furnish temperature was 20°C during forming. At this temperature, the viscosity of water is 1.0 mPas.

Fig. 3. a) Measured pressure under the wire during forming. b) Measured height of the fiber suspension column during forming. c) Velocity of the suspension surface calculated from the height data. d) Resistivity of the filtered sheet calculated from Eq. 5. In this case basis weight was 30 g/m² and the SR level was 85 (Trial point 22 in Table 2).

Trial points

An overview of the trial setup for the study is shown in Table 2. The parameters included in the table are SR level, basis weight (BW_sheet), vacuum level (P) and water removal time (T). With SR43, SR72, and SR97 two forming measurements and with SR85 three forming measurements were performed for each trial point. In Table 2 the values of P and T are averages over the successive measurements. Notice that the pressure levels were not identical for different SR levels. For SR97, water removal times are shown for all measurements, as T was clearly higher with the second run due to the fines clogging the wire very efficiently (the first measurements were always performed with a clean wire). With other furnishes, water removal times were similar with successive measurements.

Table 2. Trial Setup for the Study

Methods

The resistivity of the filtered sheet during forming

The flow of water through a filtered sheet is usually described by Darcy’s law (Bear 1972), as follows,

(1)

where v is the superficial velocity of water, µ is the water dynamic viscosity, P is the pressure difference over the sheet, L is the thickness of the sheet, and k is the sheet permeability. Equation 1 neglects inertial effects, which usually play a minor role in the flow through fibre sheets (Wildfong et al. 2000).

In practice, determination of the thickness of the fiber sheet is very challenging during the filtering process (Kataja and Hirsilä 2001; Paradis et al. 2002). In such a case Darcy’s law (Eq. 1) can be written in the form,

(2)

where D is the drainage resistance of the sheet. If the basis weight is known, Eq. 2 can be written in the form (Ingmansson 1952; Ingmansson and Whitney 1954; Ramaswamy 2003, Roux and Rueff 2012),

(3)

where BW is the basis weight, and

(4)

is the resistivity of the filtered sheet. (Notice that between the permeability k and resistivity K there is the relation , where is the density of the fibers in the filtered sheet.)

In the vacuum-assisted sheet former, one has to take into account both the flow resistance, R, due to the wire and the porous plate supporting it, and the hydrostatic pressure of water, ρgh. In this case, the velocity during the forming process is at time t

  (5)

Model for the resistivity K

Sayegh and Gonzales (1995) studied fluid flow through pre-formed sheets made from various paper-making furnishes with vacuum levels up to 35 kPa. They found that the resistivity of a fiber sheet could be described with good accuracy using Eq. 6,

(6)

where I is the pressure impulse density,

(7)

and β, α, and ɣ are pulp-dependent material parameters. The model assumes that the sheet behaves as a first order approximation like a viscoelastic Maxwell material, wherein the elastic behaviour of the sheet is reflected in the term and the plastic behaviour in the term . The parameter is called the zero-pressure resistivity of the furnish.

Koponen et al. (2015) showed that the resistivity at the end of the filtering process could be described well with Eq. 6. However, the obtained very small and negative values of γ for some furnishes suggested that Eq. 6 might need to be modified. Koponen et al. (2016) suggested for resistivity the modified formula, as follows:

(8)

Here

(9)

is a term that takes into account the different impulse histories of sheet fiber layers (c is the consistency of the pulp). In the work of Koponen et al. (2016), Eq. 8 gave values for γ similar to (Sayegh and Gonzales 1995) for various furnishes having SR levels between 15 and 40, basis weights between 80 and 570 g/m², and vacuum levels between 5 and 70 kPa. The model also predicted in Koponen et al. (2016) the consistency development of an NSSC furnish in a Fourdrinier pilot machine with a reasonable accuracy up to the waterline. In the present work, likely due to lower basis weights, Eq. 8 gave only slightly different model parameters to Eq. 6. Thus, Eq. 6 was used as the model of sheet resistivity.

RESULTS AND DISCUSSION

Retention

Retention was over 95% for SR43 and SR72 and over 90% for SR85. For these furnishes, the correct dosage of the furnish could be obtained with a few test sheets. However, for SR97 retention was lower and strongly dependent both on the basis weight and the vacuum level (Fig. 4). Finding the correct amount of SR97 furnish was thus challenging, and the basis weights of the final SR97 sheets varied somewhat.

As can be seen below (e.g. Fig. 18), retention was approximately constant during the filtering process for SR43 and SR72. With SR85 retention was initially slightly lower, especially with higher vacuum levels and lower basis weights. SR97 behaved very differently: retention was initially much lower than in the later parts of the process.

In Fig. 4, the retention of SR97 decreased strongly with an increasing vacuum level due to the stress forces becoming strong enough to deform the flexible fines and fibrils to fit into the pores of the wire and the filtered sheet. The clearly improved retention with an increasing basis weight is likely due to SR97 having a critical basis weight of the filtered sheet, after which the retention clearly improves (see Fig. 7 and explanations therein).

A regression analysis was performed for SR97 in which retention, RET (expressed in %), was the dependent variable. The basis weight (BW, g/m²) and vacuum (P, kPa) were the independent variables. The following power law type formula worked very well:

(10)

Table 3 shows the obtained values for the regression coefficients a, b, and c.

Fig. 4. Retention of the SR97 furnish as a function of basis weight for three vacuum levels. (This figure also shows the retention for test points that are not included in Table 2.)

Table 3. Regression Coefficients of Regression Analysis for Retention of SR97 Furnish

Water Removal Time

Figure 5 shows the water removal time as a function of the sheet basis weight for different SR levels. The vacuum levels have been indicated in Fig. 5 with color coding. Water removal time obviously increased with increasing basis weight, decreased with increasing vacuum level, and increased strongly with an increasing SR value. With a higher SR level, there is more solid surface area in the filtered sheet that causes viscous friction to the flow. Moreover, there are more fines that can travel and clog pores in the wire and the filtered sheet.

A regression analysis was performed separately for each SR level, for which the dependent variable was the water removal time (T, seconds). The basis weight (BW, g/m²) and the vacuum level (P, kPa) were the independent variables. A power law type model worked very well. The regression formula can be described by Eq. 11,

(11)

where a, b, and c are the regression parameters. Table 4 shows the obtained values of the parameters.

Table 4 shows that power b increased with increasing SR value. The dependence of the water removal time on the basis weight was linear for SR43. For SR85 and SR97, the basis weight dependence was quadratic. SR72 with b = 1.6 was in a transient zone between linear and quadratic behaviour. For SR43, SR72, and SR85 the water removal time was approximately inversely related to the square root of P. This indicates that the sheet became compressed significantly during the process. For SR97 water removal time was almost inversely related to P. This is likely due to very poor retention at the beginning of the filtering, especially with higher vacuum levels, which leads to a very rapid initial water removal rate.

Fig. 5. Water removal time of the four furnishes as a function of basis weight for different vacuum levels (color-coded)

Table 4. Regression Coefficients of Regression Analysis for Water Removal Time of Different Furnishes

Suspension Column Height as a Function of Time

Figure 6 shows the suspension column height as a function of time for a) low and b) high vacuum levels. The basis weight was here 40 g/m², but the curves were similar for other basis weights. The water removal time increased strongly with an increasing SR level. The shape of the curves was similar for SR43, SR72, and SR85; height decreased approximately exponentially as a function of time. SR97 behaved very differently. Initially, during the first second of forming, height decreased very quickly, and the SR97 curve followed the SR43 and SR72 curves being below the SR85 curve. Then the flow speed decreased significantly and the water removal time of SR97 was finally much lower than for the other furnishes.

Fig. 6. Measured height as a function of time for different SR levels. Basis weight is ca. 40 g/m². a) Low vacuum level; b) High vacuum level

Figure 7 shows that the shapes of the SR97 height curves were similar with different basis weights and vacuum levels. In all cases there seemed to be an inflection point, shown with a red circle, at which the forming dynamics changed. This was likely due to a strong change in retention. Initially, retention was very low and most of the SR97 fibrils traveled through the wire – the growth of the filtered sheet was slow and was mainly due to the longest fibrils. When the filtered sheet reached a critical basis weight BW_cr, which was dependent on the vacuum level, retention clearly improved and the water flow through the wire slowed down significantly.

Fig. 7. Measured suspension column height as a function of time for SR97. The red circles show the locations of the inflection points, where the forming dynamics changes.

A regression analysis was performed where the total height change Δh (expressed in millimeters) by the inflection point was the dependent variable. The basis weight calculated from the fiber dosage (BW_ini, g/m²) and vacuum (P, kPa) were the independent variables. It was found that the following regression formula worked very well:

(12)

Table 5 shows the obtained values for the regression coefficients a, b, and c. Δh increased with an increasing vacuum level due to decreasing retention (Eq. 10). Δh was approximately inversely related to BW_ini. This supports the hypothesis suggested above that retention started to increase significantly when the filtered sheet had reached a critical basis weight.

Table 5. Regression Coefficients of Regression Analysis for of SR97 Furnish