Abstract
This research investigated the potential of some European wood species for use in the manufacturing of the back plates of violins as an alternative to the quite rare curly maple wood. An experimental modal analysis was employed for this purpose using the impact hammer method. The modal analysis was performed both on the top and back plates, as individual structures, and then after being integrated into the violin body. The modal analysis envisaged the determination of the eigenfrequencies (natural frequencies), the number of spectral components, and the quality factor, as important indicators of the acoustic performances of a musical instrument. A multi-criteria analysis based on the values obtained for these indicators allowed interesting findings concerning the acoustic properties of the selected wood species (hornbeam, willow, ash, bird-eye maple, walnut, and poplar). Same as curly maple, they all have special aesthetics, but only hornbeam, willow, and ash wood proved to have acoustic potential as well.
Download PDF
Full Article
Modal Analysis of Violin Bodies with Back Plates Made of Different Wood Species
Vasile Ghiorghe Gliga,a Mariana Domnica Stanciu,b Silviu Marian Nastac,c,b and Mihaela Campean a,*
This research investigated the potential of some European wood species for use in the manufacturing of the back plates of violins as an alternative to the quite rare curly maple wood. An experimental modal analysis was employed for this purpose using the impact hammer method. The modal analysis was performed both on the top and back plates, as individual structures, and then after being integrated into the violin body. The modal analysis envisaged the determination of the eigenfrequencies (natural frequencies), the number of spectral components, and the quality factor, as important indicators of the acoustic performances of a musical instrument. A multi-criteria analysis based on the values obtained for these indicators allowed interesting findings concerning the acoustic properties of the selected wood species (hornbeam, willow, ash, bird-eye maple, walnut, and poplar). Same as curly maple, they all have special aesthetics, but only hornbeam, willow, and ash wood proved to have acoustic potential as well.
Keywords: Violin; Top plate; Back plate; Violin body; Modal analysis; Fundamental frequency; Number of spectral components; Quality factor
Contact information: a: Transilvania University of Brasov, Faculty of Wood Engineering, Universitatii Str. 1, 500036 Brasov, Romania; b: Transilvania University of Brasov, Faculty of Mechanical Engineering, Politehnicii Str. 1, 500024 Brasov, Romania; c: Dunarea de Jos University of Galati, Faculty of Engineering and Agronomy in Braila, MECMET Research Center, Calea Calarasilor Nr. 29, 810017 Braila, Romania; *Corresponding author: campean@unitbv.ro
Graphical Abstract
INTRODUCTION
The violin is a “fundamental tool of human expression that reveals and reflects the historical, technological, social, and cultural aspects of time and people” (Perez and Marconi 2018). Created at the beginning of the 16th century in the northern part of Italy (Hutchins 1983), the violin is still considered to be one of the most exquisite musical instruments, not only due to its major role, sometimes as a solo instrument in the orchestra and in a wide variety of musical genres, but also due to the fact that each violin actually represents a fine work of art made from wood.
Spruce and maple are the two most favored wood species used by luthiers for the crafting of violins. The top plate with the specific f-holes, the soundpost, and the bass bar (placed inside the violin body) are made of resonance spruce wood (Picea abies), while the back plate, the ribs, and the neck are usually made of curly maple (Acer pseudoplatanus). The bridge and the fingerboard are made of ebony. Lime or willow wood are used for some elements of the counter-ribs.
As far as the raw material for the violin top plate is concerned, no other wood species could ever surpass the characteristics and acoustic performances of resonance spruce wood. Its main features are the homogeneous structure, with narrow (1 to 3 mm), regular annual rings, with a low latewood proportion (less than 20 to 35% of the annual ring width), which gives a light coloration of the wood, fine narrow rays, relatively low density (below 450 kg/m3), low resin content (without resin pockets), uniform color, the white, golden-white, and silky gloss of the wood, and straight grain (Bucur 2006; Beldeanu 2008; Stanciu and Curtu 2012).
The resonance spruce is harvested during the vegetative rest period because in the vegetation season with the presence of sap, which contains resin as well, the acoustic characteristics of the wood are depreciated. The tree diameter must be chosen to obtain logs with diameters of 400 to 600 mm (Dinulica et al. 2019). This diameter range is required for the radial cutting of the elements used for musical instruments. The trees are felled when the outside temperature is 3 to 5 °C, under heavy snow conditions, to avoid deterioration during felling.
An important aspect regarding the raw material preparation technology is the drying method used and its duration. The resonance wood is usually naturally dried until a moisture content of 15% is reached. To dry further, kiln-drying must be employed, considering that in the temperate climate zone, the moisture bound by adsorption inside the wooden cell walls cannot be eliminated from wood at ambient temperature (Campean and Marinescu 2012). It is true that kiln-drying must be avoided, as much as possible, because even mild kiln-drying conditions cause internal stresses and phenomena at the microcellular level that destroy the acoustic qualities of the resonance wood (Stanciu and Curtu 2007; Obataya et al. 2020). As a consequence, the drying duration of wood for musical instruments might last from 3 to 12 years or even more, depending on the quality class of the violin (Dinulica et al. 2015).
When it comes to choosing the material for the back plate of the violin body, luthiers have a higher degree of freedom than for the top plate. Although the back plate also plays an important acoustic role as part of the resonance body (where the top and back plate assembly must operate as a membrane, capable to transmit vibrations and to amplify them), the material characteristics imposed for this part of the violin are not as strict anymore. Thus, Hutchins (1981) considered that, from the acoustical point of view, the top plate and the back plate of a violin must have the same tone, and the frequency of mode 2 in the top plate should be within 1.4 % of that in the back. The tuning of the two plates can be obtained even if different wood species are used, but the tuning effect can be sensed only after assembling the two plates and creating the violin body.
Fig. 1. Violin back plate made of curly maple (manufactured by Gliga Instruments, Reghin, Romania)
Fiber-reinforced polymers or composites can be also used as an alternative for manufacturing the violin plates (e.g. Damodaran et al. 2015; Duerinck et al. 2018; Philips and Lessard 2018).
Coming back to the choice of the wooden raw material for the violin back plate, curly maple (Acer pseudoplatanus) is the favorite, due to its decorative pattern (Fig. 1). The wavy grain in maple is a natural “defect” that increases not only the aesthetic value, but also the acoustical properties of this wood species (Bucur 2006; Stanciu 2020).
Even if curly maple is the favorite choice, alternative wood species are worth being investigated as well, considering the scarcity of curly maple resources in the world’s forests and the fact that this species is also in demand in the furniture industry.
However, reference literature provides only minimal information on attempts of using alternative wood species in the construction of musical instruments. For example, Bond (1976) (cited by Bucur 2006) proposed the tropical wood called merbau or mirabou (Intsia bakeri) for the back of the violin. Another option could be balsa wood (Waltham 2009), or mansonia as well as many other species from the tropical regions of South America (Delgado et al. 1983; De Souza 1983) or from Australia (Bucur and Chivers 1991). A study performed by Torres and Torres-Martinez (2015) revealed that the use of alternative woods (e.g., Cupressus lindleyi, Dalbergia paloescrito, Dalbergia granadillo Pittier, and Cordia dodecandra DC.) for the back plate and ribs of a guitar does not cause considerable variations in the middle and high-frequency ranges of its vibratory response. This finding was also confirmed by Carcagno et al. (2018), who tested guitars with back plates made of Brazilian rosewood, Indian rosewood, mahogany, sapele, and walnut.
Therefore, the authors considered that a study in this direction would be most welcome, and they decided to investigate the opportunity to use alternative European wood species instead of the quite rare curly maple wood, for the back plate of violins. The modal analysis was performed both on the individual top and back plates (Fig. 2a and 2b) and on the violin body (Fig. 2c), obtained after assembling each pair of plates.
Fig. 2. Tested material: a) Violin top plate; b) Violin back plate; and c) Violin bodies obtained by assembling a pair of top and back plates
As a novelty, the modal analysis envisaged the determination of the mechanical (vibratory) behavior of the violin resonance box within the spectrum of low and medium frequencies, for different wood species. The eigenfrequencies (natural frequencies), the number of spectral components, and the quality factor, as important indicators of the acoustic performances of a musical instrument.
Significant contributions regarding modal analyses on violins or violin components were previously brought by e.g. Marshall (1985), Bissinger and Olivier (2007), and Pyrkosz and Van Karsen (2013).
The first eigenfrequency (f0), usually called fundamental frequency, is essential for the tuning of the musical instrument. For violins, the fundamental frequency is within the range 270 to 280 Hz (Donoso et al. 2008).
The second eigenfrequency (also called, second vibration mode) reflects the contribution of the top plate within the violin body that acts like a Helmholtz-type resonator, and the fifth eigenfrequency (which usually is the frequency with the highest amplitude) reflects the contribution of the back plate. The latter one characterizes the sound intensity: for a violin to produce a strong sound, the amplitude of the vibrational response of the sound plate should be as high as possible (Barlow 1997; Wegst 2006). According to reference literature (Hutchins 1981; Jansson 2002; Donoso et al. 2008), this frequency, which is below 1000 Hz, gives the violin its musical timbre and it acts as a fingerprint/signature for each instrument.
The number of eigenfrequencies varies from one wood species to another. It depends on the wood structure, its density, and its elastic properties. The number of eigenfrequencies determines the number of spectral components that give the violin its musical timbre. The higher this number, the larger the sound spectre covered by the violin. The maximum frequency (fmax) together with the fundamental frequency (f0) define the limits of the spectral domain of the violin acoustics.
The quality factor (Q) is one of the most important parameters for evaluating the acoustic quality of resonance wood (Wegst 2006). It characterizes the time needed for the sound to fade away after the excitation has stopped. For musical instruments, the quality factor should be as high as possible (to ensure slow sound damping). Reference literature indicates: Q = 105 for resonance spruce wood (Filipovici 1964) and Q = 80 to 105 for curly maple wood (Bucur 2006).
The comparative analysis of the values for these indicators on violin bodies with back plates made from different wood species allowed interesting findings concerning the acoustic potential of some species to be used for the manufacturing of musical instruments.
EXPERIMENTAL
Materials
The material used within this research consisted of 14 violin top plates made of resonance spruce wood (Picea abies), without f-holes (at this stage) (Fig. 2a) and with identical geometrical features (shape and dimensions specific to 4/4 violins). Additionally, 14 violin back plates (two of each species) with identical geometrical features (shape and dimensions specific to 4/4 violins), two reference back plates made of curly maple wood (Acer pseudoplatanus) (Fig. 2b), and six alternative wood species: hornbeam (Carpinus betulus), walnut (Juglans regia), willow (Salix alba), ash (Fraxinus excelsior), poplar (Populus nigra), and bird-eye maple wood (Acer saccharinum) (Fig. 3) were utilized in this study. Lastly, 14 violin bodies (without neck, bridge, and soundpost), obtained by assembling each top plate with a back plate, so that two violin bodies for each combination of species resulted were also used.
All violin components used within this experimental research were manufactured at Gliga Musical Instruments, Reghin (Romania).
Fig. 3. Experimental violin back plates made of alternative wood species
Table 1 presents the values of the density and the modulus of elasticity along the grain direction (EL) of the eight wood species used as raw materials for the manufacturing of the experimental violin parts, these being the most relevant physical and mechanical properties that influence the acoustic properties of wood.
Table 1. Density and MOE of the Wood Species Used for the Manufacturing of the Experimental Violin Plates
Sources: * Bucur 2006; ** Wagenführ 2008; *** The Wood Database (2020)
As one may notice, two categories of alternative species were used: some dense ones, with a density close to the one of maple wood (e.g., hornbeam, walnut, ash, and bird-eye maple), and a second category of softer hardwoods, with a similar density to spruce (e.g., willow and poplar).
However, it is important to emphasize that the main selection criterion for the alternative wood species for the back plates was the aesthetic value. Different cutting modes and some natural defects were admitted to obtain violin back plates with special visual impact, similar to the way in which curly maple was chosen by the old school violin makers (its acoustic properties being proved only later on).
Methods and Equipment
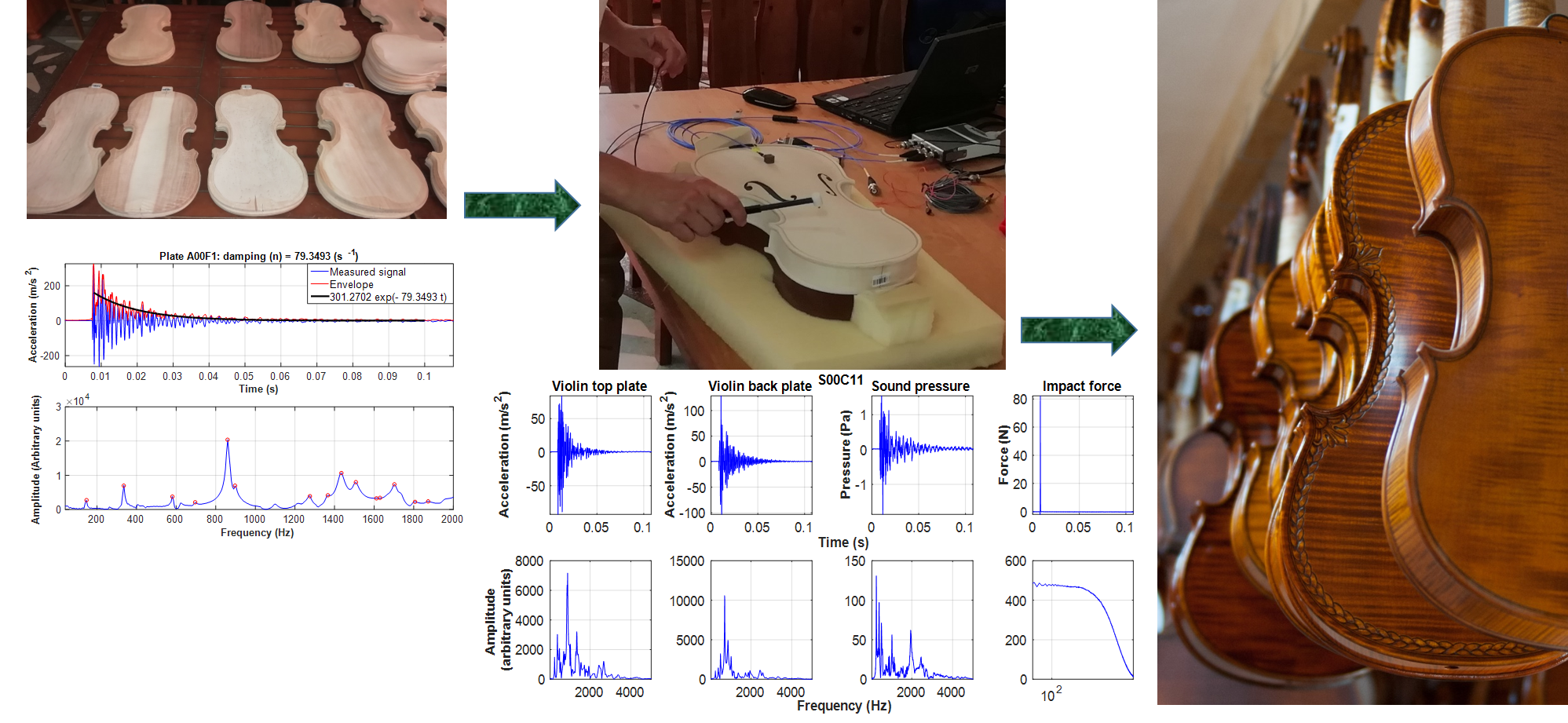
The experimental modal analysis (EMA) applied (Giron-Sierra 2017; Nastac and Debeleac 2018; Nastac 2019) involved two steps. In the first, the 28 plates were tested as individual structures (Fig. 4a). Then, the 14 violin bodies (Fig. 4b) were tested, where the output signals were captured from both coupled plates (top and back) simultaneously.
After weighing each violin component, the modal analysis by the dynamic method was applied consecutively to the top and back plates, and then to the violin bodies, one by one. Each sample (violin component) was supported with spring elements, to simulate the free structure (Fig. 4). Then, the sample was excited by an impact hammer type B&K 8204, and its response was captured by an accelerometer type B&K 4517-002 for the violin bodies two identical accelerometers were used, one placed on the top plate and the other on the back plate).
The technical data of the accelerometers are given below:
– Sensitivity: 10 mV/g,
– Measurement range: 500 g pk,
– Frequency range 2 to 10,000 Hz,
– Resonant Frequency ≥ 55 kHz,
– Size (height x length x width): 10.2 mm x 10.2 mm x 10.2 mm,
– Weight 4 g.
Both the hammer and the accelerometers were obtained from Brüel & Kjær (Nærum, Denmark).
Fig. 4. Experimental set-up: a – modal analysis of the individual top and back violin plates;
b – modal analysis of the violin body; 1 – sample (a – violin plate; b – violin body); 2 – spring element; 3 – impact hammer; 4 – accelerometer (a – one accelerometer; b- two accelerometers, one on the top and one on the back plate); 5 –cables; 6 – DAQ; 7 – laptop
Repeated measurements were performed. The spectrum flatness of the input signal (provided by the impact hammer) was one of the main parameters monitored during the experimental test. Each tested situation was strictly monitored related to this characteristic, which was a decisive factor in the acquisition procedure of accelerations.
The received signals were transmitted through a conditioning device to a dynamic signal acquisition system (DAQ) – NI USB-9233 manufactured by National Instruments (Austin, TX, USA), connected to a laptop. The signal was acquired via a special application developed by the authors in LabVIEW © (National Instruments, Release 2008, Austin, TX, USA), and the data were processed and analyzed via an application developed in MatLab© (MathWorks, Release 2008, Natick, MA, USA).
The interference noise within the acquired signals does not affect the spectral investigation taking into account that the goal of measurements had exclusively regarded the evaluation of modal frequencies (which were provided by the relevant peaks within the spectrum). However, the acquired signals were filtered using a band-pass filter (0.1…5000 Hz), taking into account that the objective of this study deals with low frequency range behavior of violin plates (1…2000 Hz). In addition, it has to be mentioned that spectral noise of accelerometers is 500…50 μg/Hz0.5, within the frequency range of interest.
Through analyzing the exponential damping curve and the spectral signal composition for each tested violin part, the number and values of the eigenfrequencies (the fundamental frequency f0, then the up-following ones, f1, f2, …, fn = fmax, and also the dominant frequency, namely that with the highest amplitude) and the quality factor (Q) were obtained. Through counting the number of frequencies from the frequency spectrum obtained by the classical Fast Fourier Transform (FFT) procedure, the number of spectral components was established, and this provided evidence to be able to draw noteworthy conclusions concerning the spectral composition (richness of tone color) of the violin body, as a function of the wood species chosen for the back plate.
Finally, to detect which of the tested wood species has good potential to be used for the manufacturing of violin back plates, a multi-criteria analysis was performed, based on the following criteria: the dominant frequency (C1), the maximum frequency attained (C2), the number of spectral components (C3), and the quality factor (C4). All criteria were invested with identical weight (25%). A mark on a scale from 5 (minimum) to 10 (maximum) was attributed for each criterion to each species. Then, the weighted score (S) was calculated for each species according to Eq. 1,
(1)
where Nij is the mark (from 5 to 10) attributed for each criterion (I = 1 … 4) to each species (j = 1…7), and Wi is the weight of that criterion (in this case: W1 = W2 = W3 = W4 = 0.25).
Afterwards, the species were ranked according to the values obtained for the weighted score (S).
RESULTS AND DISCUSSION
Table 2 presents the codification and mass of the analyzed individual top and back plates (as pairs), as well as the codification and mass of the resulted violin bodies after assembling each pair.
Table 2. Codification and Mass of the Experimental Violin Plates and Violin Bodies
The results of the modal analysis performed on the violin top and back plates, as individual structures, are presented in Fig. 5, where the graphic representations of the acceleration as a function of time, and of the amplitude as a function of frequency, are given. The graphs are drawn within the interval 0 to 2000 Hz to highlight the area of the dominant frequencies.
Fig. 5. Fast Fourier Transform results for violin plates tested as individual structures (a – top plate, and b through h – back plates of different wood species)
The sound pressure and impact force spectra are presented in Fig. 6.
Fig. 6. Fast Fourier Transform results for violin bodies
Tables 3 and 4 present the recorded values of the most representative eigenfrequencies (the fundamental frequency f0, the second frequency f1, the frequency at the highest amplitude, and the maximum frequency fmax), as well as the number of spectral components, and the quality factor for each experimental plate.
Table 3. Modal Analysis Results Obtained from the Violin Top Plates Made of Resonance Spruce
The values of the fundamental frequencies recorded for the 14 violin top plates made of resonance spruce wood ranged between 116 Hz and 165 Hz, with an average of 150 Hz. For the second vibration mode, the eigenfrequencies ranged between 280 Hz and 378 Hz, with an average of 346 Hz. Similar values were obtained by Hutchins (1981), who reported the following eigenfrequencies for resonance spruce wood: 80 Hz, 147 Hz, 222 Hz, 304 Hz, and 349 Hz; these values were obtained via the holographic interferometry method. Hutchins (1981) also mentions that variations for the values of the low frequencies may occur due to the variability of the plate mass, dimensions, and rigidity.
The frequencies measured at maximum amplitude within the present research ranged between 799 Hz and 1025 Hz. The highest frequencies measured were 2185 to 4022 Hz, with an average of 3045 Hz.
The number of spectral components registered for the top plates as individual structures ranged between 16 and 29, with an average of 22.
The quality factor ranged within the interval 71 to 80, with an average of 77.
Table 4. Modal Analysis Results Obtained from the Violin Back Plates Made of Different Wood Species
It was established that the values of the fundamental frequency of the back plates were different from one species to another. Thus, for the back plates made of willow and poplar (which are low-density wood species), the fundamental frequencies were the lowest registered ones, with values ranging around 61 Hz (for willow), and 125 to 129 Hz (for poplar). In increasing order of the values of this parameter, they were followed by the back plates made of ash (f0 = 153 to 164 Hz), then walnut (f0 = 177 Hz), then hornbeam (f0 = 275 to 293 Hz), and finally curly maple and bird-eye maple (f0 = 305 to 330 Hz).
The highest frequencies were also recorded for the denser hardwood species. Thus, the back plates made of hornbeam, walnut, curly maple and bird-eye maple reached up to a maximum frequency (fmax) of 4500 Hz, which can be explained due to their high density and MOE.
As far as the number of spectral components is concerned, it was observed that the range of values was similar to the one obtained for the top plates, namely 18 to 30. As expected, the highest values were obtained for the curly maple plates, followed by the ones made of hornbeam, ash, and walnut (the species with highest density among the selected ones).
Regarding the quality factor, it was clearly noticed that the values for the back plates were higher than for the top plates. They ranged within the interval of 91 to 100. The maximum values were obtained for the hornbeam plates, followed by the ones made of bird-eye maple and then curly maple.
Table 5 presents the results of the modal analysis performed on the 14 violin bodies obtained after assembling each top plate with a back-plate. According to the two accelerometers used (one placed on the top plate and one on the back plate of the violin body), two sets of values were obtained for each violin body. These correspond to the top plate and back plate, respectively, after being embedded.
Table 5. Modal Analysis Results Obtained After Embedding the Violin Top and Back Plates into Violin Bodies
The Fundamental Frequency
Unlike the top plates tested as individual structures, which were actually simple membranes whose vibration was exclusively governed by the material characteristics, the top plates embedded within the violin bodies have a different rigidity due to the contour restraints and the adding of the resonance bar. This aspect leads to a relatively constant spectral zone, with no regard to the combination of species used for the top and back plate. As reported in reference literature, the fundamental frequency of the violin body is obtained from the vibration mode of air, the violin body being a Helmholtz-type resonator (Bissinger 2008; Donoso et al. 2008; Trapasso 2013). As a consequence, one can appreciate that the first vibration mode only depends on the geometry of the violin body and the air volume inside. This explains why the fundamental frequency obtained within the present research is almost identical for all violin bodies tested. Both the fundamental frequencies recorded on the top plate and on the back plate, as well as the acoustical pressure, ranged within the interval of 238 Hz and 262 Hz, the most frequent value being 256 Hz (Table 5). Similar results were obtained by Torres and Torres-Martinez (2015), who identified the fundamental frequency around 300 Hz and Donoso et al. (2008), who found values ranging within 270 to 280 Hz.
The Second Eigenfrequency
The second eigenfrequency was also found with identical values on the top plate and on the back plate, but with a higher amplitude for the top plates. As noticed from Table 5, the violin bodies with back plates made from willow and bird-eye maple wood registered close values to the “A” musical note (440 Hz), while the others were by a half-tone or one tone lower than the tuning note. These characteristics emphasize the high potential of becoming musical instruments, considering that the adding of the neck, the bridge, the soundpost, the strings, and the finishing material modify the acoustic properties of the final musical instrument.
The Dominant Frequency
The dominant frequency was determined by FFT analysis. This frequency usually corresponds to the fifth vibration mode (also called the “ring mode”). As shown in Table 5, its values are totally different for the top plate and the back plate. Figure 7 illustrates the three categories in which the selected species can be classified according to the value of the dominant frequency. The low-density species (willow and poplar) form a first group, characterized by the lowest dominant frequencies (> 700 Hz). In the second group, with dominant frequencies between 750 Hz and 799 Hz, in which ash and bird-eye maple are included. The back plates made of walnut, hornbeam, and curly maple wood displayed the highest values of the dominant frequency (850 to 950 Hz). The values for curly maple wood are confirmed by Hutchins (1981), Jansson (2002), and Donoso et al. (2008).
Fig. 7. Variation of the dominant frequency of the violin body for back plates made of different wood species (the graph indicates the maximum value obtained for each wood species)
The Maximum Frequency
As given in Table 5 and illustrated in Fig. 8, the lowest values of the maximum frequency (fmax) were attained by the violin bodies with the back plate made of poplar wood (fmax < 1172 Hz), and the highest value was obtained by one of the violin bodies with the back plate made of curly maple wood (fmax = 2795 Hz).
Fig. 8. Variation of the maximum frequency of the violin body for back plates made of different wood species (the graph indicates the maximum value obtained for each wood species)
Fig. 9. Macrostructure of the back plate S00S1 made of hornbeam wood, cut tangentially and having numerous pith flecks (a), compared to the back plate S00S2 that was also made of hornbeam wood but cut radially and with rare pith flecks (b)
Good results (fmax = 2400 to 2500 Hz) were also obtained by the violin bodies with the back plate made of willow wood.
For walnut, bird-eye maple, and hornbeam, quite great differences were recorded between the two violin bodies, which represented the same combination of species because in some cases obtaining an aesthetical violin prevailed. Thus, one of the violin bodies with the back plate made of walnut wood (S00S4), had remarkable aesthetics due to the presence of sapwood and heartwood, but the structural non-homogeneity decreased its maximum frequency considerably: for S00S4, fmax was 1514 Hz, while for S00S3 fmax was 2130 Hz.
The same thing happened to one of the violin bodies with the back plate made of hornbeam wood (S00S1) (Fig. 9a), which was cut tangentially for aesthetical reasons and had numerous pith flecks, compared to the other one (S00S2) (Fig. 9b), with a more uniform structure: for S00S1, fmax was 1678 Hz, while for S00S2 fmax was 2472 Hz.
The Number of Spectral Components
The richest number of spectral components was recorded for a back plate made of curly maple (28 frequencies), which was close to the one obtained for the resonance spruce top plates (29 frequencies). Ash, willow, hornbeam, and walnut back plates were situated at some distance (with 18 to 21 frequencies), while the lowest number of spectral components (10 frequencies) was again recorded for the poplar back plates (Fig. 10).
Fig. 10. Variation of the number of spectral components of the violin body for back plates made of different wood species (the graph indicates the maximum value obtained for each wood species)
The Quality Factor
The highest values of this indicator of acoustic quality were recorded for the back plates made of bird-eye maple, ash, hornbeam, and willow (Q > 80). Surprisingly, these species outpaced curly maple wood, for which the maximum quality factor was only 74. Again, the lowest values were obtained for the back plates made of poplar wood (Q < 60) (Fig. 11).
Fig. 11. Variation of the quality factor for violin bodies with the back plate made of different wood species (the graph indicates the maximum value obtained for each wood species)
Table 6 presents the results of the multi-criteria analysis performed to detect which of the tested wood species has better potential to be used for the manufacturing of violin back plates.
Table 6. Multi-criteria Analysis Concerning the Wood Species Potential to be Used for the Manufacturing of the Violin Back Plate
According to the results obtained within the present research, it seems that hornbeam and willow wood, followed closely by ash wood, have good potential to be successfully used to manufacture the back plate of violins, while poplar wood does not seem suitable at all. Walnut and bird-eye maple wood registered unsteady results (one probe was good, while the other was weak at certain criteria), which is probably due to their non-homogenous structure.
It is important to emphasize that, to obtain comparable results, the violin plates used within the present research had identical geometrical features. In reality, violin makers adjust the thickness profile of each plate before integrating it into the violin body to tune the instrument.
Future research studies envisage the influence of the thickness variation of the violin plates upon their acoustical performances, as well as a modal analysis and an acoustical analysis of the violins “in white” (after adding the neck, bridge, soundpost, and strings to the tested violin bodies). The authors expect these further researches to enhance a firmer statement regarding the acoustic potential of the selected wood species and their suitability to be used for the manufacturing of violin back plates.
CONCLUSIONS
1. The modal response of the tested violin plates, both top and back plates, changes when they are integrated into the violin bodies. It was found that, after embedding, the three elements of the Helmholtz-type resonator (the top plate, the volume of air inside the violin body, and the back plate) have a common fundamental frequency, situated within the range 238 to 262 Hz. Through comparing the behavior of the plates as individual structures and then as part of the violin body, it was found that the back plates made of high-density species (e.g., hornbeam, walnut, ash, and maple) suffered a decrease of their fundamental frequency after integration into the violin body, while the back plates made of willow and poplar increased their fundamental frequency value. This was due both to the contour restraints and the acoustic compensation between the two plates in the violin construction.
2. The highest frequencies were recorded for the back plates made of hornbeam, walnut, curly maple, and bird-eye maple as individual structures (with an average of 4500 Hz). The top plates made of resonance spruce wood reached maximum frequencies of up to 4022 Hz as individual structures and up to 2838 Hz when integrated into the violin body. The lowest values of the maximum frequency after assembling the violin bodies were recorded for the back plates made of poplar wood (approximately 1100 Hz).
3. The number of spectral components was kept constant for the top plates and tended to decrease for the back plates after their integration into the violin body, this was due to the contour restraints of the plates produced by fixing them into the violin body. Referring to the influence of the wood species, the highest number of spectral components was recorded for one of the violin bodies with a back plate made of curly maple wood (28 frequencies), followed by the violin bodies with ash back plates (21 and 19 frequencies). The lowest number of spectral components was recorded for the violin bodies with back plates made of poplar and bird-eye maple wood.
4. The quality factor had a similar behavior to that of the number of spectral components. A clear tendency of modification after embedding into the violin body was observed only in the case of the back plates, namely the quality factor decreased, especially in the case of the poplar and hornbeam back plates.
5. According to the results obtained within the present research, hornbeam and willow wood, followed closely by ash wood have good potential to be successfully used to manufacture the back plate of violins, while poplar wood does not seem suitable at all.
REFERENCES
Barlow, C. Y. (1997). “Materials selection for musical instruments,” Proceedings of the Institute of Acoustics 19, 69-78.
Beldeanu, E. C. (2008). Forest Products, Transilvania University Publishing House, Braşov, Romania. (In Romanian)
Bissinger, G. (2008). “Structural acoustics model of the violin radiativity profile,” J. Acoust. Soc. Am. 124(6), 4013-4023. DOI: 10.1121/1.3006957
Bissinger, G., and Olivier, D. (2007). “3-D laser vibrometry on legendary old Italian violins,” Sound and Vibration Magazine 41(7), 10-15.
Bond, C. W. (1976). “Wood anatomy in relation to violin tone,” J. Int. Wood Sci. 7(3), 22-26.
Bucur, V. (2006). Acoustics of Wood, 2nd Ed., Springer-Verlag, New York, NY, USA.
Bucur, V., and Chivers, R. C. (1991). “Acoustic properties and anisotropy of some Australian wood species,” Acustica 75(1), 69-74.
Campean, M., and Marinescu, I. (2012). “Thermal treatments of wood,” in: Lumber Drying, Transilvania University Publishing House, Braşov, Romania. (In Romanian)
Carcagno, S., Bucknall, R., Woodhouse, J., Fritz, C., and Plack, C. (2018). “Effect of back wood choice on the perceived quality of steel-string acoustic guitars,” J. Acoust. Soc. Am. 144(6), 3533-3547. DOI: 10.1121/1.5084735
Delgado, O. A., Vazquez Montano, V., Carmona-Valdovinos, T. F., and Benito, M. (1983). Fabricacion y Restauracion de Instrumentos Musicales Clasicos de Cuerda i Arcos [Manufacturing and Restoration of Classical String and Bow Musical Instruments], Inst Nacional de Investigaciones sobre Recursos Bioticos, Xalapa, Veracruz, Mexico.
De Souza, M. R. (1983). Classification of Wood for Musical Instruments (Ser Tech No. 6), Departamento de Pesquisa, Instituto Brasileiro de Desenvolvimento Florestal, Brasilia, Brazil.
Dinulica, F., Albu, C. T., Borz, S. A., Vasilescu, M. M., and Petritan, I. C. (2015). “Specific structural indexes for resonance Norway spruce wood used for violin manufacturing,” BioResources 10(4), 7525-7543. DOI: 10.15376/biores.10.4.7525-7543
Dinulica, F., Albu, C. T., Vasilescu, M. M., and Stanciu, M. D. (2019). “Bark features for identifying resonance spruce standing timber,” Forests 10(9), Article number 799. DOI: 10.3390/f10090799
Donoso, J. P., Tannus, A., Guimaraes, F., and Correa de Freitas, T. (2008). “The physics of the violin,” Rev. Bras. Ensino Fís. 30(2), 2305.1-2305.21. DOI: 10.1590/S1806-11172008000200006
Filipovici, J. (1964). The study of wood. Volume 2, Didactic and Pedagogic Publishing House, Bucharest, Romania. (In Romanian)
Giron-Sierra, J. M. (2017). Digital Signal Processing with Matlab Examples, Volume 1 Signals and Data, Filtering, Non-stationary Signals, Modulation, Springer Science and Business Media, Singapore. DOI: 10.1007/978-981-10-2534-1
Hutchins, C. M. (1981). “The acoustics of violin plates,” Scientific American 245(4), 170 ff, 1-11.
Hutchins, C. M. (1983). “A history of violin research,” Journal of the Acoustical Society of America 73(5), 1421-1440. DOI: 10.1121/1.389430
Jansson, E. (2002). “Vibration properties of the wood and tuning of violin plates,” Acoustic for Violin and Guitar Makers, (http://www.speech. kth.se/music/acviguit4/ part5.pdf), Accessed 20 Jan 2020.
Marshall, K. D. (1985). “Modal analysis of a violin,” Journal of the Acoustical Society of America 77(2), 695-709. DOI: 101121/1.3922338
Nastac, S. (2019). Experimental Procedures. Evaluative Setups and Tests, Galati University Press, Galati. (In Romanian)
Nastac, S., and Debeleac, C. (2018). “Assessment on operational modal identification refining of a structural element,” Proceedings of the 14th International Conference Acoustics and Vibration of Mechanical Structures (AVMS-2017), 323-329. DOI: 10.1007/978-3-319-69823-6_38
Obataya, E., Zeniya, N., and Endo-Ujiie, K. (2020). “Effects of seasoning on the vibrational properties of wood for the soundboards of string instruments,” J. Acoust. Soc. Am. 147(2), Article number 998. DOI: 10.1121/10.0000723
Perez, M.A., and Marconi, E. (2018). “Wooden musical instruments different forms of knowledge,” in: Book of End of Wood MusICK COST Action FP1302, Cite de la Musique – Philharmonie de Paris, Paris, France
Pyrkosz, M., and Van Karsen, C. (2013). “Comparative modal tests of a violin,” experimental Techniques 37, 47-62. DOI: 10.1111/j.1747-1567.2012.00831.x
Stanciu, M. D., and Curtu, I. (2007). “The music of wood,” PRO LIGNO Journal 3(2), 61-68.
Stanciu, M. D., and Curtu, I. (2012). Dynamics of Classical Guitar Structure, Transilvania University Publishing House, Braşov, Romania. (In Romanian)
Stanciu M.D., Cosereanu C., Dinulica F., and Bucur V. (2020). “Effect of wood species on vibration modes of violins plates,” Eur. J. Wood Prod.78, 785-799.
The Wood Database (2020). “Wood finder,” The Wood Database, (https://www.wood-database.com/wood-finder/), Accessed 20 Jan 2020.
Torres, J. A., and Torres-Martinez, R. (2015). “Evaluation of guitars and violins made using alternative woods through mobility measurements,” Archives of Acoustics 40(3), 351-358. DOI: 10.1515/aoa-2015-0038
Trapasso, L. (2013). Feature-based Analysis of the Violin Tone Quality, Master’s Thesis, Politecnico di Milano, Milan, Italy.
Wagenführ, R. (2008). Holzatlas, Carl-Hanser Verlag GmbH & Co. KG, Munich, Germany.
Waltham, C. (2009). “A balsa violin,” American Journal of Physics 77(1), Article number 30. DOI: 10.1119/1.2996482
Wegst, U. G. K. (2006). “Wood for sound,” American Journal for Botany 93(10), 1439-1448. DOI: 10.3732/ajb.93.10.1439
Article submitted: April 23, 2020; Peer review completed: June 28, 2020; Revised version received and accepted: August 14, 2020; Published: August 24, 2020.
DOI: 10.15376/biores.15.4.7687-7713
