Compression responses of bio-cellular luffa sponges

An, X., Sui, Q., Sun, F., Ma, Z., Jiang, S., Ji, B., and Fan, H. (2015). "Compression responses of bio-cellular luffa sponges," BioRes. 10(4), 8426-8438.

Abstract

Crushing behaviors of luffa sponges were studied through mechanical experiments. Controlled by four-order hierarchical and anisotropic structures, luffa sponges exhibit anisotropic responses along axial, radial, and circumferential directions. The ultra-thin but stiff inner surface layer dominates the crushing behavior, endowing the axially compressed luffa cylinder with structural integrity, enhancing the elastic deformation and yielding strength. In radial, circumferential, and lateral compressions, after removing the inner surface layer, luffa sponges are compliant and have large quasi-linear deformation before densification, without a plateau characterized by yielding and deformation. Immersed into water, crushed luffa sponge cylinders recover their geometry completely. However, compression strength is only partially restored. Gradual damage of the inner surface layer in water immersing/drying cycles greatly weakens the compression strength. In the case of removal of the inner surface layer, crushed luffa sponge cylinders completely restore their quasi-linear deformation ability during the water immersing/drying cycles.

Download PDF

Full Article

Compression Responses of Bio-Cellular Luffa Sponges

Xiyue An,^a,bQianqian Sui,^aFangfang Sun,^aZhiyuan Ma,^aShu Jiang,^a Bing Ji,^aand Hualin Fan ^a,b

Keywords: Natural cellular luffa sponge; Hierarchical structure; Mechanical properties; Mechanical testing

Contact information: a: College of Mechanics and Materials, Hohai University, Nanjing 210098, China; b: State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;

Corresponding authors: fhl02@mails.tsinghua.edu.cn (Hualin Fan); sunff1986@126.com (Fangfang Sun)

INTRODUCTION

Bio-cellular materials, observed in biological systems, have hierarchical structures (Lakes 1993; Fratzl and Weinkamer 2007; Chen and Pugno 2013); these materials exhibit excellent mechanical properties at remarkably low density (Taylor et al.2011; Fan et al. 2014; Wang et al. 2014; Anbukarasi and Kalaiselvam 2015). The luffa sponge is one such material containing a complex, interconnecting pore structure (Shen et al.2012; 2013; 2014; Chen et al. 2014). Investigation into the structure and properties of biological foam-like materials may enable scientists and engineers to reveal novel functional mechanisms and further develop biologically inspired materials with engineered properties. Shen et al. (2012, 2013, 2014) reported measurements of stiffness, strength, and energy absorption characteristics of the luffa sponge. Chen et al. (2014) revealed that the structure influences the mechanical behavior of the luffa sponge. Their study revealed the anisotropic properties of luffa sponges through crushing experiments. The tensile strength of a single fiber was reported to be approximately 100 MPa (Chen et al. 2014).

Based on studies of Shen et al. (2012, 2013, 2014) and Chen et al.(2014), the anisotropy and hierarchy of luffa sponges and their influences to the crushing behaviors were explored quantitatively in this paper.

LUFFA SPONGE STRUCTURE

The luffa sponge has a hierarchical cellular structure. Macroscopically, the luffa sponge is a cylinder (the 1^st order structure) and the cylinder contains macro-pore structures with three parts (the 2^nd order structure): a cylindrical shell, a core structure, and more than three macro-pores, forming a hollow cellular cylinder, as shown in Fig. 1. The letters X, Y, and Z denote axial, circumferential, and radial directions, respectively. Mesoscopically, the cylindrical shell and the core structure are cellular structures (the 3^rd order structure), containing interconnected struts and open meso-pores, as shown in Fig. 2. Microscopically, the strut of the luffa sponge exhibits a two-order hierarchical hollow cellular tube (the 4^th order structure). Four-order hierarchical porosities make the luffa sponge ultra-light and usually lighter than 0.1 g/cm³.

Fig. 1. Macro-structure of a luffa sponge from the (a) outside surface, (b) cross section, and (c) inner surface

Mesoscopically, luffa sponges have highly complex anisotropic properties. On the outer surface, fibers extend along the circumferential direction (X-axis), and there are only a few continuous fibers in the vertical direction (Y-axis), as shown in Fig. 2. The inside surface contains an ultra-thin and stiff planar network of fibers that primarily extend in the vertical direction, as shown in Fig. 2. Therefore, the cylindrical shell has two parts, similar to that of stiff lamellae in a compliant matrix. One part is the outside surface layer, whose thickness is close to that of the cylindrical shell and has fibers distributing circumferentially. The second part is an ultra-thin and stiff lamina, with thickness of a single fiber strut and fibers mainly extending vertically.

Fig. 2. Mesostructure of a luffa sponge showing the (a) outside surface, (b) cross section, and (c) inner surface, using an optical microscope

EXPERIMENTS

Luffa sponges were bought from Shi Wang Enterprise Co., Ltd. (China). These sponges are usually used as cleaning materials in China. The store-bought luffa sponge cylinders were approximately 15 cm long. The ends of the cylinders were removed, and the test samples were cut from the central part. To understand the mechanical performances of luffa sponges, uniaxial compression experiments were performed using a 50-kN Instron (USA) test machine at a loading rate of 2 to 5 mm/min. Characteristics of the samples are listed in Table 1.

Table 1. Characteristics of Luffa Sponge Cylinders

To reveal the influence of water, the crushed luffa sponge cylinders, listed in Table 2, were immersed into water for 24 h and dried at room temperature for one week. Then, the water-immersed and dried cylinders (WDCs) were uniaxially compressed.

Table 2. Characteristics of Luffa Sponge Cylinders after Water-Immersing/Drying Cycles

RESULTS AND DISCUSSION

Crushing Behaviors

As shown in Fig. 3, uniaxial crushing curves of luffa sponge cylinders have three stages: elastic deformation, stable crushing deformation plateau, and densification. When the core part of the cylinder is removed (Fig. 3(b) and 3(d)), the samples have identical deformation curves to those with the core (Fig. 3(a) and 3(c)). For samples without the core, a macro-shell buckling mode was observed, as shown in Fig. 4(a). Other cylinders failed at local sites of crimpling, as shown in Fig. 4(b). The uniaxial compression strength of the luffa sponge material, defined by the ratio of the force to the area of the luffa sponge material from the shell and the core (Area of the macro-pore structure was not included), was approximately 0.3 MPa. The crushing ratio (densification strain) is usually greater than 0.7 for luffa sponge materials. Thus, the level of energy absorption is approximately 0.21 J/cm³ (Fig. 3(d), A10). When the density of the material is approximately 0.07 g/cm³, the energy absorption is 3.0 J/g (Fig. 3(d), A10). The energy absorption capacities of luffa sponges are better than those of polymer and aluminum foams (Shen et al. 2012). Compared to lattice materials (Fan et al. 2014), luffa sponge materials exhibit improved specific energy absorptions, as shown in Fig. 3. A fourth-order hierarchical structure enables luffa sponges to be more weight-efficient than second-order hierarchical hollow-strut Ni–P micro-lattices (Schaedler et al. 2011).

The inner surface layers of samples 1a to 8a were removed and the samples were compressed to determine if the inner surface layer would impact the strength, as shown in Fig. 5. For all samples, the strength greatly decreased when removing the inner surface layer. For samples without the core, the strength was below 0.15 MPa, about a 50% reduction from the initial value, as shown in Fig. 5(a). The deformation curves had different characteristics.

Fig. 3. Crushing behaviors of luffa sponges (a) A1-A3; (b) A4-A6; (c) A7-A9 and (d) A10-A12, and energy absorbing abilities per unit (e) volume and (f) mass

Fig. 4. Crushing modes of luffa sponges (a) without or (b) with core structures

For samples without core, the deformation curve was quasi-linear before the densification strain reached 0.8, as shown in Fig. 5(b). Yielding and deformation plateaus were not observed in any of the samples; therefore, it is difficult to define the strength based on such a deformation curve. The linear deformation stiffness, , is calculated by

(1)

where is the densification strain and is the densification strength of the luffa sponge material. Assuming , .

Without the inner surface layer, the modulus of the luffa sponge is comparable to its densification strength. Energy absorption ( W) is calculated by

(2)

Without the inner surface layer, luffa sponges were found to have decreased energy absorption at a rate of 0.16 J/cm³. This was approximately 30% less than the energy absorption of luffa sponges with the inner surface layer in place.

Fig. 5. Uniaxial crushing behaviors of luffa sponges (a) with and (b) without core structures. The dotted line denotes that the inner surface layer of the sample has been removed.

Block materials cut from the cylindrical shell, as shown in Fig. 1(c), were compressed along the radial direction. As shown in Fig. 6(a), the deformation curves are quasi-linear before the strain approaches the densification strain, which is similar to the uniaxial compression curve of the luffa sponge material without inner surface layer (Fig. 5). The results reveal that the inner surface layer has little contribution to the radial crushing behavior.

Block materials were compressed along the circumferential direction, as shown in Fig. 6(b). The deformation curve in circumferential compression was different from the quasi-linear curve in radial compression. With circumferentially distributed fibers, the block exhibited three deformation stages: elastic deformation, linear deformation after yielding, and densification. The strength was usually smaller than 0.1 MPa. After yielding, the deformation was linear before densification.

Fig. 6. Crushing behaviors in the (a) radial and (b) circumferential directions

Luffa sponge cylinders were compressed laterally, as shown in Figs. 7 and 8. Characteristics of samples are listed in Table 1. Before densification, the curves are quasi-linear, as shown in Fig. 7. When mechanically compressed, the cellular foam in the cylindrical shell was condensed; however, the pore structure did not deform, as shown in Fig. 8.

As the compressed area gradually increased, it subsequently increased the stress load on the fibers. Then the pores were compressed and plastic hinges formed in the shell. The inner surface layer had little contribution to these plastic hinges because it exhibited reduced bending motion. Contractions among fibers supply anti-crushing stability to resist lateral compression.

Fig. 7. Lateral crushing behaviors of luffa sponges along the (a) long and (b) short axes

Behavior after Water-Immersing/Drying Process

Five water-immersing/drying cycles were tested, as shown in Fig. 9. After these cycles, crushed cylinders were restored their initial geometric shape completely, similar to results by Shen et al. (2014). The WDCs exhibited similar geometric deformation curves as the initial samples. But the yielding strength was less than one-third of the initial strength.

Fig. 8. Lateral crushing modes of luffa sponges along the(a) long and (b) short axes.

Fig. 9. Crushing behaviors after the water immersing/drying cycles for (a) A7, (b) A8,(c) A9, (d) A10, (e) A11, (f) A12, (g)A13, and (h) A14

Fig. 10. Uniaxial crushing behaviors of luffa sponges (a) with and (b) without core structures after one water-immersing/drying cycle. The dotted lines denote samples with the inner surface layer removed.

When the inner surface layer was removed, different responses after the water-immersing/drying process were acquired, as shown in Fig. 10. Linear deformation characterizes the response of WDCs without inner surface layer. Furthermore, the curves were consistent with those of initially compressed samples before water-immersing/drying cycles. Therefore, the results indicate that the anti-crushing ability of WDCs without the inner surface layer was nearly restored.

Compared with observations of Shen et al. (2014), advanced understanding on the water-responsive rapid recovery of natural cellular material has been achieved. Damage of the inner surface layer of the luffa sponge may decrease the strength in water-immersing/drying cycles. Without this layer, water-responsive rapid recovery is ideal because of the deformation resistance from interactions among fibers.

Mechanism

The cylindrical shell structure behaves as an ultra-thin lamella covering a thick and compliant bio-cellular matrix. The ultra-thin and stiff lamellae may bear the load, while the thick but compliant cellular matrix supports the ultra-thin layer from buckling. Without the stiff lamellae, the cylinder deforms linearly and has ultra-low load capacity. Without the compliant matrix, membrane buckling controls the failure.

The modulus of elasticity and strength of the cylinder, and , can be predicted using the following equations:

(3)

(4)

(5)

(6)

(7)

(8)

In these equations, and denote the volume fraction of the inner stiff shell and the soft matrix, respectively. and denote the modulus of the inner stiff cylindrical shell and the soft matrix, respectively. and are the modulus and strength of a single fiber, respectively. and denote the thickness and width of a single fiber, respectively. is the distance between neighboring vertical fiber in the inner surface layer, is the volume fraction of the vertical fiber in the inner surface layer, and denote the inside and outside diameters of the cylindrical shell, respectively, and is the area ratio of the inner surface after removing the joint area with the core part. As suggested by Chen et al. (2014), characteristics of luffa sponge cylinders are listed in Table 3. Considering errors in estimating the dimension of the hierarchical structure, Eq. 3 suggests consistent results with the experiments.

Table 3. Characteristics of Luffa Sponge Cylinders (from Chen et al. 2014)

When the inner surface layer is removed, luffa sponge materials deform linearly before densification. The modulus is comparable to the stress. As shown in Fig. 2, fibers are perpendicular to the compression load; therefore, fibers have minimal bending and axial compression deformation. Under compression, fibers are in close contact and laterally compressed. The slope of the macro-linear deformation curve depends on the amount of the contact area. The stress and strain, and , are linearly associated using the equation below:

(9)

Contacts among fibers enhance the anti-crushing ability in lateral compression. Contact area ( ) is a variable to evaluate the stress and determined by the following equations,

(10)

(11)

where is the ultimate compression area of the sample.

Removing the inner surface layer, water-immersing/drying cycles have little influence on the crushing behaviors. Damage of the inner surface layer decreases the yield strength. However, the densification strength is identical to that of the sample without inner surface layer. Damage to the material (D) in the cycle is calculated using the following equation,

(12)

and the strength of the WDCs in the cycle is used to determine in the following equation,

(13)

where denotes the strength of the sample without water immersion. The exponent, 0.85, from Fig. 11(b) describes the weakening response of other samples. It is similar to the relationship described by Shen et al. (2014), where the exponent is 0.65. Ni-P microlattices have a similar regularity in repetitive loadings (Schaedler et al. 2011).

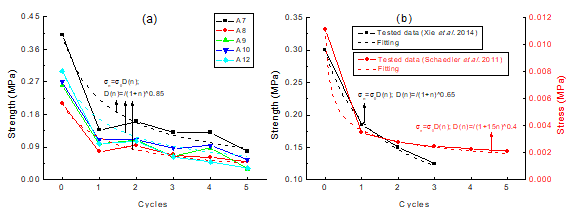
Fig. 11. Crushing behaviors after WDCs in (a) this study compared with (b) previous results from Schaedler et al. (2011) and Xie et al. (2014)

CONCLUSIONS

The hierarchy and anisotropy of the luffa sponge were investigated using quantitative analysis of the crushing behavior. Accordingly, the luffa sponge cylinder was modeled as an ultra-thin and stiff membrane surrounded by a thick and soft supporting matrix. The ultra-thin and stiff inner surface layer endows the axially compressed luffa cylinder with structural properties characterized by elastic deformation and yielding strength.
The luffa cylinders exhibit quasi-linear deformation characteristics and anisotropic responses along axial, radial, and circumferential directions. Four-order hierarchical structures permit the luffa sponge to be quite weight-efficient in resisting compression.
The ultra-thin and stiff inner surface dominates the crushing capabilities, leading to elastic deformation, yielding deformation plateau, and densification. A soft matrix, supporting stiff lamellae model was proposed and was consistent with the prediction of strength.
For radial, circumferential, and lateral compressions with or without the inner surface layer, luffa sponges exhibit quasi-linear large deformation before densification, without yielding or plateau. Contacts among fibers supply anti-crushing capability.
When immersed into water, crushed cylinders restore their geometric shape completely, and the load-bearing capacity can be partly restored. Damage of the inner surface layer during the water immersing/drying cycles decreases the strength of the fibers. Removing the inner surface layer, cylinders are able to completely restore their large quasi-linear deformation during water immersing/drying cycles.

ACKNOWLEDGMENTS

Support from the National Natural Science Foundation of China (11172089, 11372095), Program for New Century Excellent Talents in University (NCET-11-0629), State Key Laboratory of Mechanics and Control of Mechanical Structures (MCMS-0212G01, MCMS-0215G01), and Fund of State Key Laboratory of Structural Analysis for Industrial Equipment (GZ1306) are gratefully acknowledged.

REFERENCES CITED

Anbukarasi, K., and Kalaiselvam, S. (2015). “Study of effect of fibre volume and dimension on mechanical, thermal, and water absorption behaviour of luffa reinforced epoxy composites,” Mater. Des. 66, 321-330. DOI:10.1016/j.matdes.2014.10.078

Chen, Q., and Pugno, N. (2013).”Bio-mimetic mechanisms of natural hierarchical materials: A review,” J. Mech. Behav. Biomed. Mater.19, 3-33.DOI: 10.1016/j.jmbbm.2012.10.012

Chen, Q., Shi, Q., Gorb, S. N., and Li, Z. (2014). “A multiscale study on the structural and mechanical properties of the luffa sponge from Luffa cylindrical plant,” J. Biomech. 47(6), 1332-1339. DOI:10.1016/j.jbiomech.2014.02.010

Fan, H. L., Qu, Z. X., Xia, Z. C., and Sun, F. (2014). “Designing and compression behaviors of ductile hierarchical pyramidal lattice composites,” Mater.Des. 58, 363-367. DOI:10.1016/j.matdes.2014.01.011

Fratzl, P., and Weinkamer, R. (2007). “Nature’s hierarchical materials,” Prog. Mater. Sci. 52,1263-1334.DOI:10.1016/j.pmatsci.2007.06.001

Lakes, R. (1993). “Materials with structural hierarchy,” Nature 361, 511-516. DOI:10.1038/361511a0

Shen, J., Xie, Y. M., Huang, X. D., Zhou, S., and Ruan, D. (2012). “Mechanical properties of luffa sponge,” J. Mech. Behav. Biomed. Mater.15, 141-152. DOI:10.1016/j.jmbbm.2012.07.004

Shen, J., Xie, Y. M., Huang, X. D., Zhou, S., and Ruan, D. (2013). “Behavior of luffa sponge material under dynamic loading,” Int. J. Impact Eng. 57, 17-26. DOI:10.1016/j.ijimpeng.2013.01.004

Shen, J., Xie, Y. M., Zhou, S. W., Huang, X. D., and Ruan, D. (2014). “Water-responsive rapid recovery of natural cellular material,” J. Mech. Behav. Biomed. Mater. 34, 283-293. DOI:10.1016/j.jmbbm.2014.02.022

Schaedler, T. A., Jacobsen, A. J., Torrents, A., Sorensen, A. E., Lian, J., Greer, J. R.,Valdevit, L., and Carter, W. B. (2011). “Ultralight metallic microlattices,” Science 334(6058), 962-965. DOI:10.1126/science.1211649

Taylor, C. M., Smith, C. W., Miller, W., and Evans, K. E. (2011). “The effects of hierarchy on the in-plane elastic properties of honeycombs,” Int. J. Solids Struct. 48(9), 1330-1339.DOI:10.1016/j.ijsolstr.2011.01.017

Wang, X. J., Shen, J. H., Zuo, Z. H., Huang, X., Zhou, S., and Xie, Y. M. (2014). “Numerical investigation of compressive behaviour of luffa-filled tubes,” Compos. Part B: Eng.73, 149-157. DOI:10.1016/j.compositesb.2014.12.017

Article submitted: February 13, 2015; Peer review completed: July 30, 2015; Revised version received: August 1, 2015; Accepted: August 16, 2015; Published: October 30, 2015.

DOI: 10.15376/biores.10.4.8426-8438