Creep behavior of wood plasticized by moisture and temperature

Jin, F., Jiang, Z., and Wu, Q. (2016). "Creep behavior of wood plasticized by moisture and temperature," BioRes. 11(1), 827-838.

Abstract

Moisture in wood acting as a plasticizer will strongly affect the wood’s viscoelastic properties. However, achieving the desired moisture content (MC) at elevated temperatures during creep tests is difficult. The aim of this study is to accurately and systematically investigate the creep behavior of birch wood at high temperatures. Experiments were conducted using a dynamic mechanical analyzer with a relative humidity accessory coupled with polyvinylidene chloride (PVDC) film for wrapping samples. Creep behavior was examined at six MCs (0%, 6%, 12%, 18%, 24%, >30%) and 11 temperatures (5 to 105 °C). The MC of wood was strictly and accurately controlled during creep tests. Instantaneous compliance (IC) and creep compliance (CC) increased with the increase of both temperature and MC, with significant changes at higher temperatures and MCs. The effects on IC and CC were more pronounced when the subject was influenced by MC, with readings approximately three times and one time greater than those influenced by temperature, respectively. Dramatic increases in CC were found at certain temperatures and MC values. There was a complex interaction between temperature and MC on IC and CC.

Download PDF

Full Article

Creep Behavior of Wood Plasticized by Moisture and Temperature

Fangyuan Jin,^a Zhihong Jiang,^a,* and Qinglin Wu ^b

Keywords: Wood; Creep compliance; Temperature; Moisture content; DMA

Contact information: a: School of Engineering, Zhejiang Agriculture and Forestry University, Hangzhou Lin’an 311300, PR China; b: School of Renewable Natural Resources, Louisiana State University Agricultural Center, Baton Rouge, LA 70803, USA;

* Corresponding author: jzh@zafu.edu.cn; jjmoo@foxmail.com

INTRODUCTION

In wood, a natural polymer, creep under imposed stress is a viscoelastic mechanical problem that is generally encountered during processing and utilization. For example, wood creeps both during the drying of solid wood and in the process of the hot-pressing of wood composite panels, as well as during long-term loading of wood members such as roof frames, beams, columns, and walls. Therefore, to make rational and efficient use of wood, it is necessary to understand its creep properties and the influence of creep on wood and wood products in long-term service conditions.

The moisture content (MC) of wood is an important parameter affecting the creep properties of this material. Moisture in wood (MC < 30%) could affect the internal hydrogen bonds between wood polymers, thereby influencing the wood’s plasticity and deformation. There has been considerable research in creep behavior of wood at both varying MCs (Armstrong and Kingston 1960, 1962; Armstrong and Christensen 1961; Armstrong 1972; Ranta-Maunus 1975; Wu 1995; Zhan and Avramidis 2011)), and constant MCs (Youngs 1957; Clouser 1959; Kingston and Budgen 1972; Armstrong 1972; Breese and Bolton 1993; Tissaoui 1996; Jong and Clancy 2002; Kojima and Yamamoto 2005; Moutee 2006; Engelund and Salmén 2012; Hering and Niemz 2012). When creep behavior of wood is investigated at low temperatures, the controlled MC value of the wood during the test is not very difficult to realize. Creep experiments at low temperature were carried out using a water-saturated cloth (Youngs 1957) and chemical materials such as aqueous NaCl and P₂O₅ powder (Kojima and Yamamoto 2005), or by simply putting wood specimens in a conditioning room (Clouser 1959; Armstrong 1972), which consisted of a controlled humidity generator with nitrogen as the carrier gas (Engelund and Salmén 2012) and a controlled temperature and humidity chamber (Moutee 2006; Hering and Niemz 2012). With increasing temperature, however, maintaining a constant MC at elevated temperatures is very difficult because changes in MC take place simultaneously with changes in the temperature of the wood. Therefore, achieving desired MC levels at elevated temperatures during creep tests has been a technical difficulty.

Previous researchers have attempted several different ways to control and maintain a constant MC at a higher temperature during creep tests. Tissaoui (1996) applied aluminum paint in an attempt to add protection during creep tests, especially at high temperatures. Results showed an increase in creep compliance of samples when the temperature was increased, and the creep curves could only be superposed at temperatures below 65 °C because of the loss in moisture. Additionally, the resulting creep curves did not extend beyond two years. Breese and Bolton (1993) investigated the effect of temperature and MC on the time-dependent behavior of isolated earlywood specimens of Sitka Spruce in compression in the radial direction at five levels of temperature (30, 45, 60, 75, and 90 °C) and at MCs of 0%, 5%, 10%, 13%, 19%, and “green”, using two circular stainless-steel discs and butyl rubber “O” rings to seal the MC in samples. They observed the approximate linearity of the curves was lost as temperature and MC increased and also pointed out the variability between samples. Wu (1995) studied the creep properties of Douglas-fir wood in terms of compression and tension at 10% MC and at four levels of temperature (32.2, 48.9, 65.6, and 82.2 °C) in a negative pressure vessel. He obtained the relative humidity (RH) to maintain 10% MC at these temperatures by controlling the total pressure of superheated steam in a negative pressure vessel and used a control specimen suspended alongside the loaded one to monitor MC during the test. Because of the limited experimental conditions and other factors, tests on the effects of different MCs on the creep behavior of wood were not conducted. Results showed that there was some variation in the actual MC of the wood among the tests at different temperatures, creep compliance increased with the increase in temperature both in compression and tension, and temperature at the level of 82.2 °C had the greatest effect on the compressive creep. Jong and Clancy (2002) used acrylic paint to seal in the moisture of a sample of 12% MC and water heating to maintain 30% MC at elevated temperatures. Results showed that the paint and water heating controlled the increase in MC by between 1% and 3% and between 1% and 5%, respectively. They noted that maintaining MC was virtually impossible during the test.

To investigate the creep behavior of wood, the main problem is to maintain a constant temperature and RH, so as to maintain a constant MC during creep testing. Previous studies showed significant limitations in controlling and maintaining the required MC at elevated temperatures. Because of recent advances in dynamic mechanical analysis (DMA) equipped with a RH control system under strictly controlled temperature and MC conditions, it is now possible to achieve and maintain desired MC levels more accurately at elevated temperatures during creep tests. The objective of this study was to investigate the creep behavior of wood at different MCs and temperatures (up to 105 °C) using a method of sample-wrapping coupled with a DMA-RH control system.

EXPERIMENTAL

Materials

Considering a wood species with medium density (0.4 to 0.8 g/cm³) and uniformity of texture, a mature diffuse-porous birch wood (Betula pendula) with a density of 0.57 g/cm³ was chosen for the study. Twenty-millimeter-thick flat-sawn birch lumber was obtained from a floor company in Huzhou, Zhejiang, China. According to the instruction of the DMA instrument, the lumber was sawn and sanded into 3-mm-thick sample boards, and the boards were sawn again to form samples of 60 × 10 × 3 mm (length parallel to grain, width in the tangential direction, and thickness in the radial direction) in size.

Methods

Instruments

A Dynamic Mechanical Analyzer (DMA Q800) with a RH accessory (TA Instrument Company, New Castle, Delaware, USA) (Fig. 1 (a)), a WFO-710 Airing constant temperature drying oven (Ailang Instrument Company, Shanghai, China), and a temperature and humidity testing chamber (Surui Technology Development Company, Tianjin, China) were used for testing.

Fig. 1. (a) The Dynamic Mechanical Analyzer (DMA Q800) with a RH accessory and (b) a dual-cantilever configuration

Experimental design

The two main variables in this experiment were temperature and MC. Eleven levels of temperature, ranging from 5 to 105 °C in increments of 10 °C, and six levels of MC (0%, 6%, 12%, 18%, 24%, and >30%) were included. A full factorial experiment consisting of 11 levels of temperature and six levels of MC was carried out, for a total of 66 combinations. Five replicate combinations were tested, for 330 tests in total. The DMA and its DMA-RH accessory allow temperature ramp and RH adjustment to be automatically realized after being programmed. Therefore, one sample can be used to complete creep tests at 11 levels of temperature. Thus, 66 combinations were completed using six samples, and 330 tests using 30 samples.

The creep experiment was carried out in a dual-cantilever configuration (a span of 35 mm) (Fig. 1 (b)).

Sample conditioning before testing

All samples were oven-dried at 103 °C and weighed to obtain their oven-dry weight prior to sample conditioning. For tests at 0% MC, samples were wrapped with multilayers of polyethylene film prior to testing. For tests at 6%, 12%, 18%, and 24% MC, samples were conditioned in a temperature and humidity testing chamber to the desired MCs. After conditioning, samples were wrapped with multilayers of polyethylene film prior to testing. For tests at > 30% MC, samples were soaked in water prior to testing. The level of MC was checked for some samples by weighing and conditioning them before testing. The real value of the six MCs was 0.3%, 6.1%, 12.1%, 18.0%, 24.2%, and 120% (an approximate value), respectively.

Control of MC of samples during testing

A method of sample wrapping coupled with DMA-RH was employed in this study for close control of the MC of samples. Polyvinylidene chloride (PVDC) film was used to loosely wrap samples to control the MC in samples. The film was only loosely applied so that it could not affect the samples during the test. Preliminary results showed that variations in MC were very small when creep tests from 5 to 95 °C were completed (the experiment was stopped immediately after the creep test at 95 °C. Then, the sample was cooled off, weighed, and its MC was calculated.). Using the above method, the MC of samples with an initial MC of 12.1% reduced to 12.0% when creep tests from 5 to 95 °C were completed, but to 10.9% when creep tests at 105 °C were completed. If DMA-RH was employed only, variations in MC were greater. For example, the MC of samples with an initial MC of 12.2% reduced to 10.1% when creep tests from 5 to 95 °C were completed. Thus, the accuracy of maintaining MC of samples less than or equal to 95 °C during the test could be ensured by employing the method of sample filming coupled with DMA-RH control.

Determination of linear viscoelastic range (LVR)

To eliminate the effect of the value of stress or strain on viscoelastic properties such as creep compliance and to avoid involving complicated constitutive equations for a nonlinear viscoelastic body, the value of stress or strain was set within the LVR. The storage modulus of the material is independent of the imposed stress or strain within LVR. The LVR limit is defined as the value of the stress or strain at which the stress or strain plot deviates from linearity, where the degree of deviation is arbitrarily defined by the investigator (Kaboorani and Blanchet 2014). In this study, the value of the storage modulus at a strain of 0.009% was considered as the initial value of E₀ (the values of storage modulus for all wood specimens were beginning to stabilize by this time) (Jiang and Lu 2009; Kaboorani and Blanchet 2014). The point at which storage modulus was reduced by 5% was determined as the end of LVR (Sun et al. 2007; Jiang and Lu 2009; Kaboorani and Blanchet 2014). The value of stress or strain at this point was determined as a critical value of stress or strain.

To determine the critical stress, stress sweep tests were carried out with a DMA using a multi-stress mode at fixed temperatures from 35 to 255 °C in increments of 10 °C for samples with 0% MC and from 5 to 105 °C in increments of 10 °C for samples with > 30% MC. The load was between 0 and 17.5 N, and the frequency was 1 Hz.

A linear relationship was found up to 4.5 MPa at 35 °C and up to 3.1 MPa at 105 °C for the sample at 0% MC, and up to 3.8 MPa at 35 °C for the sample with > 30% MC. The LVR was reduced to less than 2 MPa when the temperature was increased to 65 °C for the sample with > 30% MC. Considering the applicable temperature range for experiments and the range of the six levels of MCs, a stress of 2 MPa was used in the creep tests to ensure that the creep deformations were mostly within the LVR.

Creep test

Creep tests were conducted with a DMA in creep mode. According to the preliminary experiments, a program was made to allow one sample to be tested successively at temperatures from 5 to 105 °C in increments of 10 °C and at the corresponding optimum humidity. The process of the creep test was creeping, heating up, equilibrating, then creeping again, and this cycle was repeated until the creep test at 105 °C was completed. In each cycle, the sample was heated up to the desired temperature (approximately 15 min) and allowed to equilibrate for 10 min. After equilibrating at the desired temperature, a stress of 2 MPa was applied, and this was held constant for 30 min while the creep strain was measured. A sample of 11 cycles took approximately 11 h in total, including nearly 1 h for conditioning before creep test. Load was not applied by default during heating up and equilibrating. These two phases were regarded as the period of recovery.

RESULTS AND DISCUSSION

The 30-min creep test results for samples at six MCs and 11 temperatures are shown in Fig. 2, expressed as compliance. As shown, with an increase in temperature, the compliance of samples at six MCs increased dramatically. Creep developed very rapidly at higher temperatures. With rising MC, the compliance of samples at the same temperature increased by varying degrees. Creep developed very rapidly at higher MC.

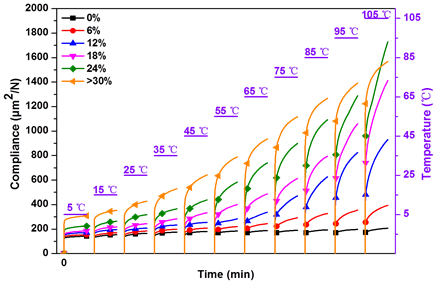
Fig. 2. Creep test results of samples at six MCs and 11 temperatures in 30-min (time of heating up and equilibrating are not proportionately presented)

The compliance shown in Fig. 2 consists of instantaneous compliance (IC) (the reciprocal of modulus of elasticity) and creep compliance (CC). The value of the compliance at which the data “creep rate” collected by DMA universal analysis was 0% was defined as the value of IC in this study. The quantity CC is then defined as the difference between the total compliance and the IC.

Instantaneous Compliance (IC)

Effect of temperature on IC

The IC of samples at six MCs and 11 temperatures is shown in Fig. 3. The IC of samples at six MCs increased continuously as temperature increased, which was consistent with the results of previous studies (Tissaoui 1996; Moutee 2006; Engelund and Salmén 2012). The IC of the samples with higher MCs was more affected by temperature than those at lower MCs. From Table 1, the IC of the sample at 0% MC at 105 °C was 152.3 μm²/N, which is an increase of 31% (0.4 μm²/N/°C, 0.3%/°C) compared with 116.1 μm²/N at 5 °C. The IC of the sample with > 30% MC at 105 °C was 966.0 μm²/N, an increase of 309% (7.3 μm²/N/°C, 3.1%/°C) compared with 236.0 μm²/N at 5 °C. The effect of temperature on the IC of the sample with > 30% MC was the greatest, approximately an order of magnitude larger than that of the sample at 0% MC.

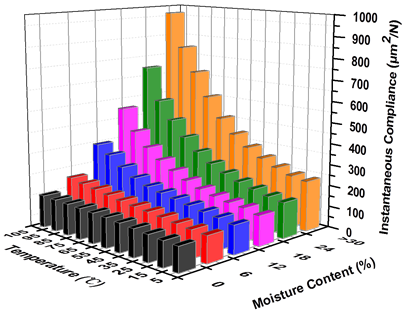
Fig. 3. Instantaneous compliance of samples at six MCs and 11 temperatures

Effect of MC on IC

From Fig. 3 and Table 2 it can be concluded that with increasing MC, the IC at the same temperature increased consistently, which was in agreement with the results of previous studies (Tissaoui 1996; Moutee 2006; Engelund et al. 2012). For example, at 5 °C, the IC with > 30% MC was 236.0 μm²/N, an increase of 103% (4.0 μm²/N/%MC, 3.4%/%MC) compared with 116.1 μm²/N at 0% MC. At 105 °C, the IC of the sample with > 30% MC was 966.0 μm²/N, an increase of 534% (27.1 μm²/N/%MC, 17.8%/%MC) compared with 152.3 μm²/N at 0% MC. The influence of MC on the IC of samples at 105 °C was the most pronounced, about six times as high as those found at 5 °C. The IC of samples at higher temperatures was more affected by MC than those at low temperatures.

In addition, from Table 1 and Table 2, it is clear that the IC of samples was more affected by MC than by temperature in the 5 to 105 °C range. The increment of IC per %MC was about four times that per degree centigrade.

Table 1. Effect of Temperature on IC at Various MCs

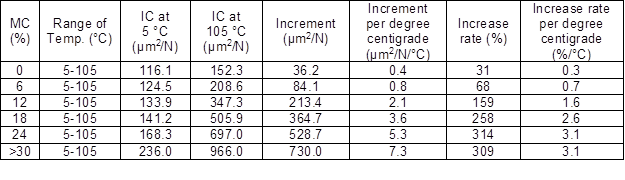
Table 2. Effect of MC on IC at Various Temperatures

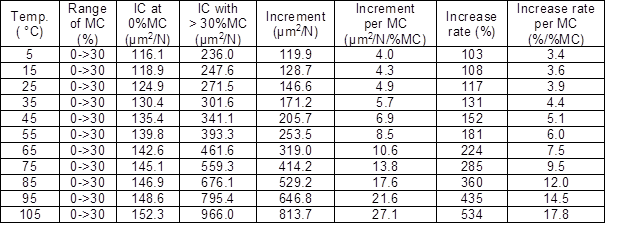
Creep Compliance (CC)

Effect of temperature on CC

The CC of samples at six MCs after 30-min creep tests in the 5 to 105 °C range is shown in Fig. 4. The CC of samples at six MCs increased by varying degrees as temperature increased. This obviously is related to the dependence of the mechanical behavior of wood (as a natural polymer) on temperature (Yang et al. 2004). In other words, when polymer components of wood are in the glassy state, the mobility of their molecular chain parts and chain segments are completely frozen, and thermal motion only occurs at fixed positions (Yang et al. 2004). When the temperature is increased, the amplitude of the thermal motion increases and the molecular chains become loose because of the repulsion between chains (Yang et al. 2004; Engelund and Salmén 2012). Secondary relaxation transitions occur in side groups or some individual chain segments. Relaxation time decreases as the temperature increases.

Temperature had a greater impact on the CC of samples at higher MCs than it did at lower MCs. From Table 3, the CC of the sample at 0% MC at 105 °C was 54.9 μm²/N, an increase of 113% (0.3 μm²/N/°C, 1.1%/°C) compared with 25.8 μm²/N at 5 °C. The CCs of the sample at 24% MC at 5 and 105 °C were 56.8 μm²/N and 1031.0 μm²/N, respectively. The rate of CC change at 24% MC was 1715% (9.7μm²/N/°C, 17.2%/°C) as influenced by temperature in the 5 to 105 °C range. The effect of temperature on the CC of samples at higher MCs was more pronounced.

Fig. 4. Creep compliance of samples after 30-min creep tests at six MCs and 11 temperatures

Table 3. Effect of Temperature on CC after 30-min Creep Test at Various MCs

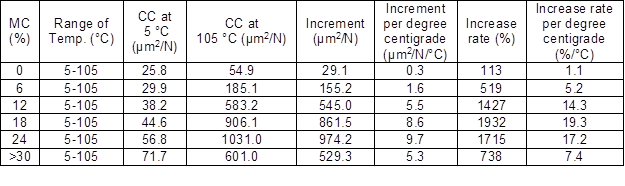
From Fig. 4, it can be observed that the CCs of the sample with > 30% MC at 95 and 105 °C were only slightly greater than that at 85 °C. This is perhaps related to a more complex phenomenon, namely mechano-sorptive creep, the creep triggered by the change in MC (Hanhijärvi and Mackenzie-Helnwein 2003). Because of the noticed loss in MC, the sample with > 30% MC was greatly affected by mechano-sorptive creep above 85 °C. At high temperatures as obtained in kiln drying, irrecoverable deformations evolve simultaneously with mechano-sorptive creep (Hanhijärvi and Mackenzie-Helnwein 2003). Therefore, irrecoverable deformation might be developed after the creep test at 85 °C, which resulted in the non-expected CCs at 95 and 105 °C.

The CC of samples at six MCs experienced a sudden and dramatic increase when temperature was higher than a certain value, as shown in Fig. 4. For the sample at 6% MC, a pronounced increase in CC at 75 °C was apparent, which could be referred to as a “jump” (here it means the temperature at which CC exhibited a step-change for the first time, see Fig. 4). Such jumps for samples at 12%, 18%, 24%, and > 30% MC were found at 65, 55 (though this jump was not very clearly shown), 45, and 35 °C, respectively. The remarkable increase of CC at 12% MC and 65 °C is coherent with the rule of thumb that states that the conditioning step at the end of wood drying schedule should not be done below 60 °C of temperature and 10% EMC. Combined with Fig. 2, it could be concluded that with the increase in MC, the temperature range at which this jump occurred was moved to the region of low temperature. This is probably because the glass transition temperature of the constituents, such as lignin, hemicelluloses, and cellulose in the wood, moved to a lower temperature with increasing MC of the sample (Salmén 1984; Kelly et al. 1987). At a certain MC, the cellulose component in wood may experience a glass transition. The glass transition temperature of cellulose decreases with increasing MC (Yin 1996).

For the sample at 0% MC, there was no significant change in CC between 5 and 105 °C, whereas a dramatic increase was discovered near 195 °C in the preliminary creep test (between 35 and 255 °C) (Tissaoui 1996).

Table 4. Effect of MC on CC after 30-min Creep Test at Various Temperatures

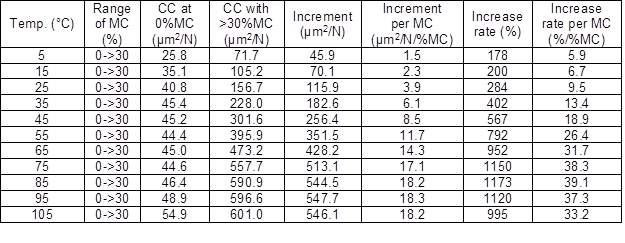
Effect of MC on CC

As shown in Fig. 4, with the increase in MC, the CC at the same temperature increased by varying degrees. Moisture acts as a plasticizer in wood (Yin 1996). With the increase in MC, the hydrogen bonds in wood, especially in hemicellulose which has a low stiffness and a high moisture absorption capacity due to a low degree of polymerization and crystallinity (Persson 2000), will be affected, broken, and re-formed, which will give rise to a weakening of the wood and a slight increase in CC, thus increasing the deformation of wood with time in response to a fixed applied stress. From Table 4, at 5 °C, the CCs of samples at 0% and > 30% MC were 25.8 μm²/N and 71.7 μm²/N, respectively, which showed that the rate of CC change was 178% (1.5 μm²/N/%MC, 5.9%/%MC) for MC in the range studied. At 85 °C, the CCs of samples at 0% and > 30% MC were 46.4 μm²/N and 590.9 μm²/N, respectively, which showed that the rate of CC change was 1173% (18.2 μm²/N/% MC, 39.1%/% MC) for MC in the range studied. The CC of samples at higher temperatures was more affected by MC than the CC at low temperatures.

From Fig. 4, it is worth noting that the CCs of the sample with >30% MC above 85 °C were less than the corresponding values at 24% MC. This may be linked to the same reason as mentioned earlier, namely mechano-sorptive creep. The sample with > 30% MC was affected more and earlier by mechano-sorptive creep compared with the sample at 24% MC due to the relatively greater loss in MC. Therefore, the irrecoverable deformation of the sample with > 30% MC generated earlier than that at 24% MC, which resulted in the CC at 85°C. More research needs to be done to obtain a better understanding of this phenomenon.

In addition, from Tables 3 and 4, it can be seen that the CC was greatly influenced by both MC and temperature, but more so by MC. The increment of CC per %MC was double that per degree centigrade.

Finally, it should be pointed out that there was an exponential relationship between the effects of MC and temperature on creep properties (IC and CC), not simply a linear relationship. The influence on IC and CC was more pronounced at both higher temperature and MC. Data in Tables 1 through 4 were only analyzed and considered approximately as a linear relationship.

Interaction between Temperature and MC

The IC and CC values of samples were greatly affected by MC at higher temperatures and also influenced by temperature at higher MCs. This is the result of the interaction between temperature and MC (Breese and Bolton 1993). Water molecules entering the cell wall result in an increased distance between cell wall elements and a decrease in cohesion, thus making the molecular chain segments become active (Engelund and Salmén 2012). Another reason is that the potential energy of wood molecular groups rises as temperature increases, which also leads to an improvement in the mobility of molecular chain segments. The interaction between temperature and MC on the IC and CC is not a simple superposition, but rather a complex functional relationship (Hanhijärvi and Mackenzie-Helnwein 2003). Further research needs to be done to give a much better interpretation of the temperature-MC interaction effect.

CONCLUSIONS

The instantaneous compliance (IC) and creep compliance (CC) of samples increased dramatically with increases in both temperature and moisture content (MC), especially when temperature and MC were both high. The IC and CC of samples with higher MCs were affected more than those with lower MCs by temperature in the 5 to 105 °C range, at approximately one order of magnitude greater. The IC and CC at higher temperatures were affected over six times as greatly by MC as those in regions of lower temperature.
Compared with temperature (from 5 to 105 °C), MC had a greater influence on the creep behavior of wood. The impact of MC on IC was three times greater than the effect of temperature, and the influence of MC on CC was one time greater than the effect of temperature.
Remarkable increases in CC for samples at 6%, 12%, 18%, 24%, and > 30% MC were discovered at 75, 65, 55, 45, and 35 °C, respectively. At higher temperatures and MCs, a complex interaction between temperature and MC on IC and CC was found.

ACKNOWLEDGEMENTS

The authors sincerely thank National Engineering and Technology Research Center of Wood-based Resources Comprehensive Utilization (Key Laboratory of Wood Science and Technology of Zhejiang Province). They are also grateful for the financial support from “The Fund for Supporting Excellent Visiting Students Overseas in the First Subject of Forestry Engineering, Zhejiang A & F University,” and Zhejiang Agriculture and Forestry University Forestry Engineering Key Discipline Open Fund (2014LYGCZ2006).

REFERENCES CITED

Armstrong, L. D., and Kingston, R. S. T. (1960). “Effect of moisture changes on creep in wood,” Nature 185(4716), 862-863. DOI: 10.1038/185862c0

Armstrong, L. D., and Christensen, G.N. (1961). “Influence of moisture changes on deformation of wood under stress,” Nature 196(4791), 869-870. DOI: 10.1038/191869a0

Armstrong, L. D., and Kingston, R. S. T. (1962). “The effect of moisture content on the deformation of wood under stress,” Austr. J. Appl. Sci. 13(4), 257-276.

Armstrong, L. D. (1972). “Deformation of wood in compression during moisture movement,” Wood Sci. 5(2), 81-86.

Breese, M. C., and Bolton, A. J. (1993). “The effect of temperature and moisture content on the time-dependent behavior of isolated earlywood specimens of Sitka Spruce (Picea sitchensis), loaded in compression in the radial direction,” Holzforschung 47(6), 523-528. DOI: 10.1515/hfsg.1993.47.6.523

Clouser, W. S. (1959). “Creep of small wood beams under constant bending load,” Report No. 2150, U.S. Forest Products Laboratory, Madison, WI.

Engelund, E. T., and Salmén, L. (2012). “Tensile creep and recovery of Norway spruce influenced by temperature and moisture,” Holzforschung 66(8), 959-965. DOI: 10.1515/hf-2011-0172

Hanhijärvi, A., and Mackenzie-Helnwein, P. (2003). “Computational analysis of quality reduction during drying of lumber due to irrecoverable deformation. I: Orthotropic viscoelastic-mechanosorptive-plastic material model for the transverse plane of wood,” J. Eng. Mech. 129(9), 996-1005. DOI: 10.1061/(ASCE)0733-9399(2003)129:9(996)

Jiang, J. L., and Lu, J. X. (2009). “Impact of temperature on the linear viscoelastic region of wood,” Can. J. For. Res. 39, 2092-2099. DOI: 10.1139/X09-119.

Jong, F., and Clancy, P. (2002). “Compression properties of wood as functions of moisture, stress and temperature,” Fire and Materials 28(2-4), 209-225. DOI: 10.1002/fam.859

Kaboorani, A., and Blanchet, P. (2014). “Determining the linear viscoelastic region of sugar maple wood by dynamic mechanical analysis,” BioResources 9(3), 4392-4409. DOI: 10.15376/biores.9.3.4392-4409

Kelly, S.S., Rials, T.G., and Glasser, W. G. (1987). “Relaxation behaviour of the amorphous components of wood,” J. Mater. Sci. 22(5), 617-624. DOI: 10.1007/BF01160778

Kingston, R. S. T., and Budgen, B. (1972). “Some aspects of the rheological behavior of wood,” Wood Sci. Technol. 6(3), 230-238. DOI: 10.1007/BF00351580

Kojima, Y., and Yamamoto, H. (2005). “Effect of moisture content on the longitudinal tensile creep behavior of wood,” J. Wood Sci. 51(5), 462-467. DOI: 10.1007/s10086-004-0676-5

Moutee, M. (2006). Modélisation du Comportement Mécanique du Bois au Cours du Séchage, Ph.D. thèse, Faculté de Foresterie et Géomatique, Université Laval, Quebec.

Persson, K. (2000). Micromechanical Modelling of Wood and Fibre Properties, Ph.D. Thesis, Lund University, Sweden.

Ranta-Maunus, A. (1975). “The viscoelasticity of wood at varying moisture content,” Wood Sci. Technol. 9(3), 189-205. DOI: 10.1007/BF00364637

Salmén, L. (1984). “Viscoelastic properties of in-situ lignin under water-saturated conditions,” J. Mater. Sci. 19(9), 3090-3096. DOI: 10.1007/BF01026988

Sun, N., Das, S., and Frazier, C. (2007). “Dynamic mechanical analysis of dry wood: Linear viscoelastic response region and effects of minor moisture changes,” Holzforschung 61(1), 28-33. DOI: 10.1515/HF.2007.006

Hering, S., and Niemz P. (2012). “Moisture-dependent, viscoelastic creep of European beech wood in longitudinal direction,” Eur. J. Wood Prod. 70, 667-670. DOI: 10.1007/s00107-012-0600-4

Tissaoui, J. (1996). Effects of Long-Term Creep on the Integrity of Modern Wood Structures, Ph.D. dissertation, Faculty of Civil Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA.

Wu, Q. (1995). “Rheological behavior of Douglas-fir as related to the process of drying,” Drying Technol. 13(8-9), 2239-2240. DOI: 10.1080/07373939508917079

Yang, T. Q., Luo, W. B., Xu, P., Wei, Y. T., and Gang, Q. G. (2004). “Polymer viscoelastic mechanics,” in: Textbook of Viscoelasticity Theory and Application, Jun Wang, Science Press, Beijing, 223-255.

Yin, S. C. (1996). “Mechanical properties of wood,” in: Textbook of Wood Science, Sici Yin, China Forestry Publishing House, Beijing, 158-183.

Youngs, R. L. (1957). “The perpendicular-to-grain mechanical properties of red oak as related to temperature, moisture content, and time,” Report No. 2079, U.S. Forest Products Laboratory, Madison, WI.

Zhan, J. F., and Avramidis, S. (2011). “Mechanosorptive creep of Hemlock under conventional drying: II. Description of actual creep behavior in drying lumber,” Drying Technol. 29(10), 1140-1149. DOI: 10.1080/07373937.2011.573154

Article submitted: August 21, 2015; Peer review completed: October 24, 2015; Revised version received: November 10, 2015; Accepted: November 13, 2015; Published: November 30, 2015.

DOI: 10.15376/biores.11.1.827-838