Abstract
In recent years, circular saw blades with thinner kerfs have been in high demand for improvement of the production yield of wood-based materials and the reduction of sawdust. In the case of ripping of solid wood, the number of teeth of a circular saw blade is normally set to 40 or 50, with a diameter of 305 mm, which allows less cutting resistance and smooth exhausting of sawdust. However, at certain rotational speeds, self-excited alternate-tooth vibration can easily occur in circular saw blades with such thin kerfs and so few teeth. Therefore, the cutting surface quality tends to be worse. In this study, the mechanism of this self-excited alternate-tooth vibration was clarified. The vibration mode and frequency were predicted by the finite element method. In addition, a circular saw blade with a body thickness 1.5 mm and 50 teeth was employed for wood-cutting experiments. The rotational speed range of the self-excited alternate-tooth vibration modes and their frequencies were investigated. When a double of the tooth passage frequency was slightly higher than the frequencies of the alternate-tooth vibration modes, an alternate-tooth vibration of the regenerative chatter type was excited, owing to the forces on the sides of the tooth.
Download PDF
Full Article
Characteristics of Self-Excited Alternate-Tooth Vibration of Circular Saw Blade
Ken Takeyama,a,b Hideyuki Yokochi,a Satoru Nishio,b and Satoru Tsuchikawa a,*
In recent years, circular saw blades with thinner kerfs have been in high demand for improvement of the production yield of wood-based materials and the reduction of sawdust. In the case of ripping of solid wood, the number of teeth of a circular saw blade is normally set to 40 or 50, with a diameter of 305 mm, which allows less cutting resistance and smooth exhausting of sawdust. However, at certain rotational speeds, self-excited alternate-tooth vibration can easily occur in circular saw blades with such thin kerfs and so few teeth. Therefore, the cutting surface quality tends to be worse. In this study, the mechanism of this self-excited alternate-tooth vibration was clarified. The vibration mode and frequency were predicted by the finite element method. In addition, a circular saw blade with a body thickness 1.5 mm and 50 teeth was employed for wood-cutting experiments. The rotational speed range of the self-excited alternate-tooth vibration modes and their frequencies were investigated. When a double of the tooth passage frequency was slightly higher than the frequencies of the alternate-tooth vibration modes, an alternate-tooth vibration of the regenerative chatter type was excited, owing to the forces on the sides of the tooth.
Keywords: Circular saw blade; Self-excited vibration; Alternate tooth vibration
Contact information: a: Graduate School of Bioagricultural Sciences, Nagoya University, Furo-cho Chikusa-ku Nagoya Aichi, Japan; b: R&D Department of Kanefusa Corporation, 1-1 Nakaoguchi Ohguchi-cho Niwa-gun Aichi, Japan; *Corresponding author: st3842@agr.nagoya-u.ac.jp
GRAPHICAL ABSTRACT
INTRODUCTION
Circular saw blades for wood machining can easily vibrate in the lateral direction owing to their thin design. This causes deterioration of the cutting surface quality and increases the sawdust and noise. In the 1980s and 1990s, the dynamic stability of circular saw blades was analyzed by many researchers (Mote and Szymani 1977; Szymani and Mote 1977; Leu and Mote 1984; Schajer 1986; Holøyen 1987; Hutton 1991; Nishio and Marui 1996). Some researchers analyzed the influence of roll tensioning on the stability of circular saw blades (Szymani and Mote 1974; Schajer and Mote 1983, 1984; Stakhiev 1999, 2003; Cristóvão et al. 2012; Zhang et al. 2014; Li et al. 2015a, 2015b; Li et al. 2016; Li and Zhang 2017). To improve stability, the impact of the temperature distribution and radial slots on the dynamic behavior of circular saw blades has also been analyzed by many researchers (Mote and Nieh 1973; Yu and Mote 1987; Ishihara et al. 2010; Yuan 2012). Some of them investigated the influence of temperature differences between the rim and center of a saw blade on its dynamic stability, whereas others analyzed how the saw blades could be stabilized by guides (Mote et al. 1981; Schajer 1986; Hutton 1991). Other researchers focused on the vibration behavior during cutting and reported on how to control and reduce this vibration. For example, cutting vibration can be suppressed by uncoupling the two vibration modes of the same nodal diameter number using outer slots on the saw blade (Yokochi et al. 1993; Nishio and Marui 1996). This can make the range of vibration of rotational speed narrow, and if any vibration occurs, the vibration amplitude becomes small. Using a high-damping saw body is also very effective for suppressing the resonance amplitude of circular saw blades. A high-damping saw body can be created using damping alloys for its construction (Hattori et al. 1993), putting a damping air film on the saw body (Trochidis 1989), or using inner slots filled with viscoelastic resin (Nishio 2005).
These studies were related to vibration control technology for saw bodies. However, self-excited alternate-tooth vibration cannot be suppressed by these technologies. Self-excited alternate-tooth vibration is defined as two teeth becoming grouped and vibrating alternately in the lateral direction of the saw blade at a particular rotational speed.
Thin-kerf circular saw blades are in high demand for the wood industry for the purposes of yield improvement and the reduction of sawdust. However, they should result in low natural frequencies. Also, higher-order natural frequencies become even lower under the influence of the gullet shape and number of gullets. When using a blade with a thin kerf and lower number of teeth, alternate-tooth vibration is induced in the practical use range of the rotational speed. This is because only the rim part of the saw blade has the same amplitude as the saw blade in these high-order and alternate-tooth vibration modes, even if the saw blade has outer and inner slots with damping material for the suppression of vibration.
In this study, the natural vibration mode and natural vibration frequency for a circular disc and saw blade models were calculated using the finite element method (FEM) modal analysis, and the generated condition of the self-excited alternate-tooth vibration mode was discussed. A tungsten carbide circular saw blade with a high damping efficiency was employed for wood cutting experiments at various rotational speeds. The range of self-excited alternate-tooth vibration modes and their frequencies were investigated, and the characteristic vibration mechanism was theoretically considered.
THEORETICAL RESONANCE CONDITION OF SELF-EXCITED ALTERNATE-TOOTH VIBRATION OF CIRCULAR SAW BLADE DURING SAWING
Theoretical Mode Analysis—Finite Element Method of Circular Disc and Circular Saw
Several studies have reported on the natural vibration modes and natural frequencies of circular discs and circular saw blades (Mote and Szymani 1977; Stakhiev 1998; Orlowski et al. 2007), where vibration modes were limited to be under five nodal diameters. This was because the purposes of these studies were for clarification of the critical rotational speed or for investigation of the behavior of a circular saw blade around the critical rotational speed. Therefore, lower natural frequencies, especially the nodal diameters n = 2, 3, or 4, were the targets of these studies. Even if suppression of the vibration during cutting was the purpose of the studies (Nishio and Marui 1996; Tian and Hutton 2001), the number of focused nodal diameters was less than 14 and higher-order modes have not been analyzed.
In this study, modal analyses of circular disc and circular saw models were performed with the aid of FEM to find the high-order natural vibration modes and high-order natural vibration frequencies. Table 1 shows the dimensions and mechanical properties of the circular disc and circular saw models used in the modal analysis. Figure 1 shows a schematic view of the circular saw model.
Table 1. Dimensions and Mechanical Properties of the Circular Disc and Circular Saw Model Used in the Modal Analysis
Fig. 1. Schematic view of circular saw model for modal analysis
Figure 2 shows the relationship between the number of nodal diameters n and natural vibration frequency for the circular disc and circular saw models. The natural vibration frequency of the circular disc model increased with increments of the number of nodal diameters. In the case of the circular saw model, the natural vibration frequency also increased with increments of the number of nodal diameters. The difference between the natural vibration frequencies of both models was over 1,000 Hz in the range more than 12 nodal diameters. The maximum number of nodal diameters was 25 (i.e., half the number of teeth), and a higher number of nodal diameters of more than 25 was not calculated in the range under 11,000 Hz.
As for the natural vibration modes at 25 nodal diameters, it was observed that two teeth became grouped and vibrated alternately. The higher natural vibration modes, for a nodal diameter of 25, generated characteristic deflections at only the rim part of the saw blade. Its natural vibration frequency was 4,822.5 Hz.
Fig. 2. Relationships between nodal diameters and natural vibration frequencies for disc and circular saw models
Alternate-tooth Vibration Mode
The FEM modal analysis of the circular saw model showed that the alternate-tooth vibration mode (Fig. 3) was n = 25. Because the alternate-tooth vibration mode was generated only at the rim part of the blade, it underscores the difficulty of suppressing that vibration mode even if the saw blade had inner slots with damping material for a high damping capacity. The amplitudes at the outer slots part were small.
Fig. 3. Alternate-tooth vibration modes (0, 25)
Estimation of Tooth Mark Patterns by Alternate-Tooth Vibration
The kind of pattern formed in a sawn surface by alternate-tooth vibration was considered from the results of the FEM modal analysis. The vibration wave on a circular saw blade is mathematically expressed as,
(1)
where D(θ, t) is the displacement of the periphery of the blade at time t, position angle θ, and number of slots s. Also, Z is the number of teeth, n is the nodal diameter number, and fn is the natural vibration frequency. On the right-hand side of Eq. 1, is a slots mode function and. It expresses that the transverse displacement at the front and back parts of the slots is small. Meanwhile, and express the vibration mode function of a circular saw blade and the time function, respectively.
The position angle of the saw teeth is:
(2)
The outer slots on the circular saw body are located between teeth and equally on the periphery of the circular saw blade. The position angle of the outer slot is expressed as:
(3)
The estimated tooth mark pattern obtained using Eqs. 1 and 2 is depicted in Fig. 4 In the figure, the following conditions are assumed: blade diameter 305 mm, rotational speed N = 70 rps (4,200 rpm), the number of slots s = 5, feed per tooth Sz = 0.06 mm, thickness of wood is 45 mm, the saw projection is 2 mm, natural frequency fn. = 4,980 Hz, and the nodal diameter number n = 25.
Fig. 4. Estimated tooth mark pattern on sawn surface using Eqs. (1) and (2).
R: 70 rps (4,200 rpm), fn: 4,980 Hz, n: 25, Z: 50, s: 5.
EXPERIMENTAL
A wood-cutting experiment was conducted to investigate the range of the self-excited alternate-tooth vibrations and sawn surfaces. The validity of the above-mentioned theoretical calculation was examined.
Circular Saw Blade
A tungsten carbide tipped circular saw blade with a high damping efficiency, saw diameter of 305 mm, kerf thickness of 2 mm, body thickness of 1.5 mm, and number of teeth of 50 was employed for the wood-cutting experiments. Five of the inner slots on the saw body were filled with damping material. The thin kerf of 2 mm and the thin body thickness of 1.5 mm were used for improvement of the yield rate and to reduce cutting resistance. And blade with 50 teeth is typically used for rip sawing and produces less cutting resistance. To check the reproducibility, an experiment was conducted using two circular saws of the same dimensions.
Experimental Condition
Western hemlock (Tsuga heterophylla Sarg., moisture content 12%, thickness: 45 mm × length: 400 mm × width: 120 mm) was ripped using circular saw blades, which was clamped by a 100 mm diameter of flange. The rotational speeds of the spindle during sawing were varied from 40 to 90 rps (2,400 to 5,400 rpm) at each step of 2 rps (120 rpm). The feed rate per tooth was set to a constant 0.06 mm. The lateral displacement during cutting was measured using a gap detector (SENTEC LS-700 HA-50S, Osaka, Japan), which was placed near the cutting point and the resolution of the gap detector was 1 µm. The data were collected with a data logger (KEYENCE NR-500, Osaka, Japan). The sampling frequency of measurement was 100,000 Hz, and the number of samples in FFT (Fast Fourier Transform) was 16,384 for each measurement. In addition, the quality of the sawn surface was observed.
RESULTS AND DISCUSSION
Vibration Frequency During Sawing
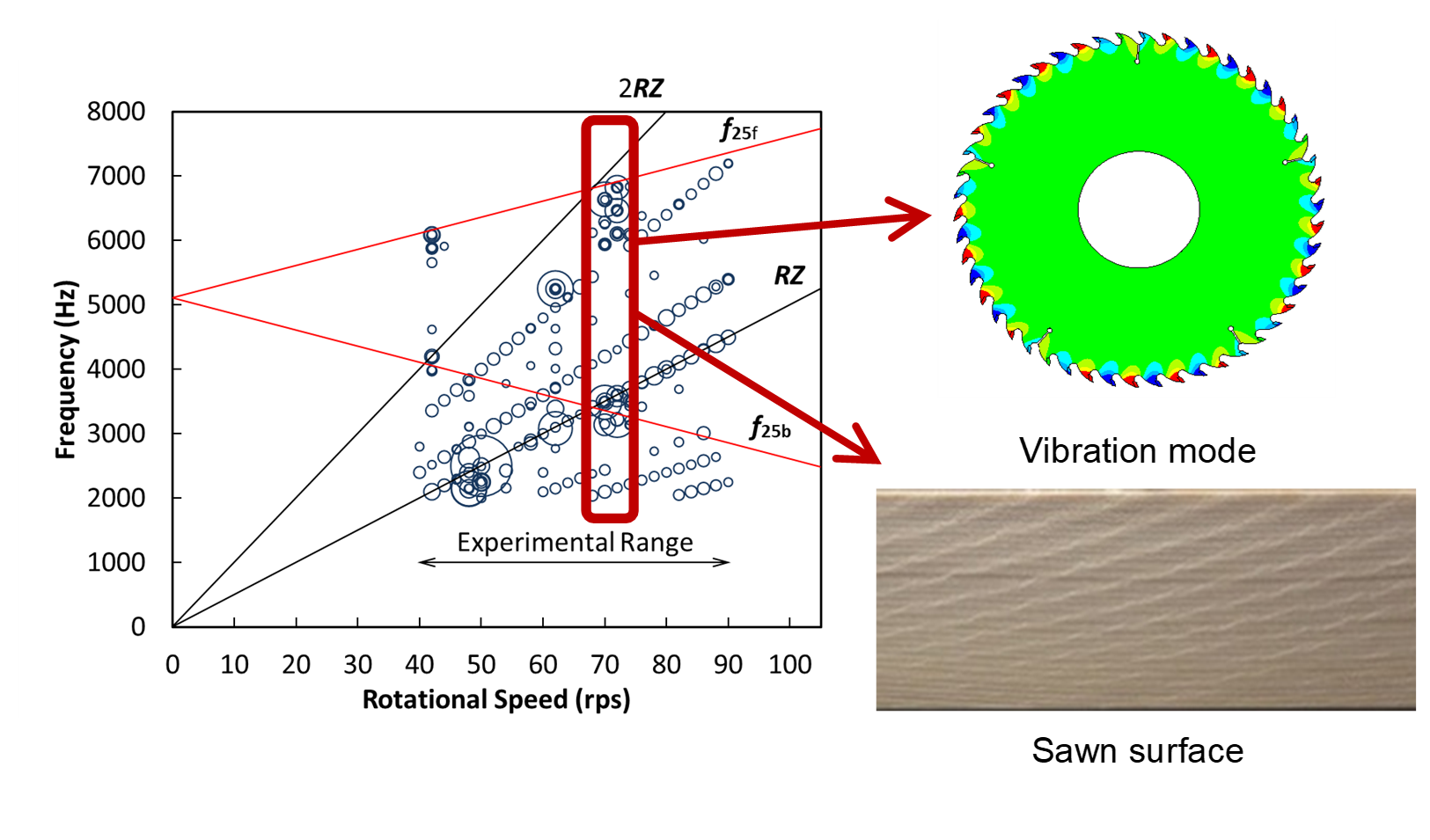
Figures 5(a) and (b) show the relationships between the rotational speed and frequency of the cutting vibration with circular saw No. 1 and No. 2, respectively. The diameter of the circles represents the amplitude level of the saw blade vibration, which was calculated with FFT. Plots below 2,000 Hz and an amplitude level below 0.0002 have been cut off for clarity. The two black lines show the tooth passage frequency R×Z and its integer multiples, where R is the rotational speed (rps) and Z is the number of teeth (= 50). The red lines show the forward wave f25f and the backward wave f25b of the alternate-tooth vibration mode f25. The forward wave f25f and backward wave are expressed, respectively, as follows.
Alternate-tooth vibration was generated, and its amplitude was excited at a rotational speed of 70 and 72 rps (4,200 and 4,320 rpm), where the forward wave f25f is slightly less than a double of the tooth passage frequency 2RZ. Additionally, alternate-tooth vibration was generated at a rotational speed, 42 rps (2,520 rpm), where the backward wave f25b is slightly less than a double of the tooth passage frequency 2RZ. The alternate-tooth vibration was confirmed in both Fig. 5(a) and (b), and it was determined that the reproducibility was achieved.
Fig. 5. Relationship between rotational speed and frequency of vibration
Fig 6. Results of spectral analysis. R: 70 rps (4,200 rpm), circular saw No.1
Figure 6 shows the result of a spectral analysis at a rotational speed of 70 rps (4,200 rpm). The forward wave f25f was 6,638.2 Hz and the backward wave f25b was 3,139.6 Hz. In addition to the forward and backward waves, peaks appeared at intervals of 350 Hz.
Fig. 7. Sawn surface when self-excited alternate-tooth vibration is generated (70 and 72 rps) or not generated (68 and 80 rps)
Because it appeared as a result of the gap detector measuring the passage of five slits at 70 rps (4,200 rpm) of the revolving blade, it was believed to be noise rather than a vibration component. The peak at 3,488.8 Hz was the pass frequency of the teeth and was believed to be the excitation frequency. At the same time, there was a peak at 3,139.6 Hz, which is a backward wave f25b. The amplitude of the forward wave f25f is dominant in this vibration. The frequency of alternate-tooth vibration f25 was estimated to be 4,888.9 Hz.
Sawn Surface Aspects with Alternate-Tooth Vibration
Figure 7 shows photographs and the roughness of sawn surfaces when self-excited alternate-tooth vibration occurred and when it did not occur. The roughness was measured using a surface roughness meter (SURFTEST SV-3100, Mitsutoyo, Kawasaki, Japan).
When no alternate-tooth vibration was generated, at rotational speeds of 68 and 80 rps (4,080 and 4,800 rpm), the maximum height of the surface roughness was from 10 to 23 µm. On the other hand, when alternate-tooth vibration was generated, at 70 and 72 rps (4,200 and 4,320 rpm), the maximum height of the surface roughness was from 40 to 60 μm. This roughness is not large but represents a loss when compared with a sawn surface under conditions in which alternate-tooth vibration is not generated, as it requires more finishing. The tooth mark pattern was consistent with the one predicted in Fig. 4. Therefore, the generated vibration was confirmed to be the alternate-tooth vibration with the mode shape and mode frequency related to 25 nodal diameters (half the number of teeth), as determined by the FEM modal analysis.
CONCLUSIONS
- With a thin-body blade, higher natural frequencies are more likely to produce vibration. Also, the frequencies of the higher modes are reduced by the number and shape of the gullets.
- The alternate-tooth vibration could not be suppressed, even by a blade with high body damping. For example, having inner slots with damping material did not help because the alternate-tooth vibration mode only involved movement of the teeth and not the inner part of the blade.
- Alternate-tooth vibration is a self-excited vibration. It is generated at the rotational speed at which the alternate-tooth vibration mode is slightly less than double the tooth passage frequency of the saw blade.
REFERENCES CITED
Cristóvão, L., Ekevad, M., and Grönlund, A. (2012). “Natural frequencies of roll-tensioned circular sawblades: Effects of roller loads, number of grooves, and groove positions,” BioResources 7, 2209-2219. DOI: 10.15376/biores.7.2.2209-2219
Hattori, N., Ando, K., Kitayama, S., and Nakashima, K. (1993). “Suppression of the whistling noise in circular saws using a newly-developed high-damping alloy,” Mokuzai Gakkaishi 39, 891-896
Holøyen, S. (1987). “Vibrations and natural frequencies of angular slot circular saws,” Holz Roh Werkst. 45, 101-104. DOI: 10.1007/BF02605981
Hutton, S. G. (1991). “The dynamics of circular saw blades,” Holz Roh Werkst. 49, 105-110. DOI: 10.1007/BF02614349
Ishihara, M., Noda, N., and Ootao, Y. (2010). “Analysis of dynamic characteristics of rotating circular saw subjected to thermal loading and tensioning,” J. Therm. Stresses 33, 501-517. DOI: 10.1080/01495731003659208
Leu, M. C., and Mote, C. D. (1984). “Origin of idling noise in circular saws and its suppression,” Wood Sci. Technol. 18, 33-49. DOI: 10.1007/BF00632129
Li, B., and Zhang, Z. (2017). “Research on the effect of yield strength of circular saw blade on roll tensioning process,” J. Wood Sci. 63, 140-146. DOI: 10.1007/s10086-016-1602-3
Li, B., Zhang, Z., Li, W., and Peng, X. (2015°). “Effect of yield strength of a circular saw blade on the multi-spot pressure tensioning process,” BioResources 10, 7501-7510. DOI: 10.15376/biores.10.4.7501-7510
Li, B., Zhang, Z., Li, W., and Peng, X. (2015b). “A numerical simulation on multi-spot pressure tensioning process of circular saw blade,” J. Wood Sci. 61, 578-585. DOI: 10.1007/s10086-015-1508-5
Li, S., Wang, C., Zheng, L., Wang, Y., Xu, X., and Ding, F. (2016). “Dynamic stability of cemented carbide circular saw blades for woodcutting,” J. Mater. Process. Technol. 238, 108-123. DOI: 10.1016/j.jmatprotec.2016.07.018
Mote, C. D., and Nieh, L. T. (1973). “On the foundation of circular saw stability theory,” Wood Fiber 5, 160-169
Mote, C. D., and Szymani, R. (1977). “A review report on principal developments in thin circular-saw vibration and control research. Part 1: Vibration of circular saws,” Holz Roh Werkst. 35, 189-196. DOI: 10.1007/BF02610942
Mote, C. D., Schajer, G. S., and Holo̸yen, S. (1981). “Circular-saw vibration control by induction of thermal membrane stresses,” J. Eng. Ind. 103, 81-89. DOI: 10.1115/1.3184465
Nishio, S. (2005). “Stable sawblade,” Proc. 17th IWMS, pp 418-420
Nishio, S., and Marui, E. (1996). “Effects of slots on the lateral vibration of a circular saw blade,” Int. J. Mach. Tool Manuf. 36, 771-787. DOI: 10.1016/0890-6955(95)00088-7
Orlowski, K., Sandak, J., and Tanaka, C. (2007). “The critical rotational speed of circular saw: Simple measurement method and its practical implementations,” J. Wood Sci. 53, 388-393. DOI: 10.1007/s10086-006-0873-5
Schajer, G. S., and Mote, C. D. (1983). “Analysis of roll tensioning and its influence on circular saw stability,” Wood Sci. Technol. 17, 287-302. DOI: 10.1007/BF00349916
Schajer, G. S., and Mote, C. D. (1984). “Analysis of optimal roll tensioning for circular saw stability,” Wood Fiber Sci. 16, 323-338
Schajer, G. S. (1986). “Why are guided circular saws more stable than unguided saws?,” Holz Roh Werkst. 44, 465-469. DOI: 10.1007/BF02608068Stakhiev, Y. M. (1998). “Research on circular saws vibration in Russia: From theory and experiment to the needs of industry,” Holz Roh Werkst. 56, 131-137. DOI: 10.1007/s001070050284
Stakhiev, Y. M. (1999). “Research on circular saws roll tensioning in Russia: Practical adjustment methods,” Holz Roh Werkst. 57, 57-62. DOI: 10.1007/PL00002622
Stakhiev, Y. M. (2003). “Research on circular saw disc problems: Several of results,” Holz Roh Werkst. 61, 13-22. DOI: 10.1007/s00107-002-0353-6
Szymani, R., and Mote, C. D. (1974). “A review of residual stresses and tensioning in circular saws,” Wood Sci. Technol 8, 148-161. DOI: 10.1007/BF00351369
Szymani, R., and Mote, C. D. (1977). “Principal developments in thin circular saw vibration and control research: Part 2: Reduction and control of saw vibration,” Holz Roh Werkst. 35, 219-225. DOI: 10.1007/BF02608337
Tian, J. F., and Hutton, S. G. (2001). “Cutting-induced vibration in circular saws,” J. Sound Vib. 242, 907-922. DOI: 10.1006/jsvi.2000.3397
Trochidis, A. (1989). “Vibration damping of circular saws,” Acustica 69, 270-275
Yokochi, H., Nakashima, H., and Kimura, S. (1993). “Vibration of circular saws during cutting Ⅱ. Effect of slots on vibration,” Mokuzai Gakkaishi (Japan) 39, 1246-1252
Yu, R. C., and Mote, C. D. (1987). “Vibration of circular saws containing slots,” Holz Roh Werkst. 45, 155-160. DOI: 10.1007/BF02627571
Yuan, L. (2012). “Influence of radial slots on the vibration characteristics of circular saw blade,” Appl. Mech. Mater. 226, 232-236. DOI: 10.4028/www.scientifi c.net/AMM.226-228.232
Zhang, M. S., Zhang, Y., Ke, J. J., Li, X. W., and Cheng, L. B. (2014). “The influence of tangential roller pressure on the stability of circular saw blade,” Appl. Mech. Mater. 614, 32-35. DOI: 10.4028/www.scientifi c.net/AMM.614.32
Article submitted: February 11, 2021; Peer review completed: March 14, 2021; Revised version received and accepted: April 3, 2021; Published: April 13, 2021.
DOI: 10.15376/biores.16.2.3840-3850
