Compression test of thermally-treated beech wood: Experimental and numerical analysis

Abstract

Experimental and numerical analysis of a compression test carried out on samples of as-received and thermally-treated beech (Fagus sylvatica L.) wood is presented. In a normal climate, samples with the dimensions of 20 x 20 x 20 mm were exposed to static compressive loads parallel and transverse to the grain. Afterwards, the test was modelled using the finite element method. It was confirmed that, after thermal modification, the wood’s density decreased and the stiffness in both tested directions increased. After the thermal treatment, the strength of beech wood increased in the direction parallel to the grain and decreased in the direction transverse to the grain. Based on the comparison of experimental and numerical results, it is possible to use the hyperelastic constitutive law to reasonably model the force and displacement obtained in the compression test samples.

Full Article

Compression Test of Thermally-Treated Beech Wood: Experimental and Numerical Analysis

Gorazd Fajdiga,^a Boštjan Zafošnik,^b,c Bojan Gospodarič,^a and Aleš Straže ^a,*

Experimental and numerical analysis of a compression test carried out on samples of as-received and thermally-treated beech (Fagus sylvatica L.) wood is presented. In a normal climate, samples with the dimensions of 20 x 20 x 20 mm were exposed to static compressive loads parallel and transverse to the grain. Afterwards, the test was modelled using the finite element method. It was confirmed that, after thermal modification, the wood’s density decreased and the stiffness in both tested directions increased. After the thermal treatment, the strength of beech wood increased in the direction parallel to the grain and decreased in the direction transverse to the grain. Based on the comparison of experimental and numerical results, it is possible to use the hyperelastic constitutive law to reasonably model the force and displacement obtained in the compression test samples.

Keywords: Thermally-treated beech wood; Mechanical properties; Numerical simulation 

Contact information:  a:  Department of Wood Sciences and Technology, Biotechnical Faculty, University of Ljubljana, Jamnikarjeva 101, SI-1000 Ljubljana, Slovenia; b:  The College of Industrial Engineering, Mariborska Cesta 2, SI-3000 Celje, Slovenia; c:  Prometheus, Boštjan Zafošnik s.p., Tacenska Cesta 125E, 1000 Ljubljana, Slovenia; *Corresponding author: ales.straze@bf.uni-lj.si 

INTRODUCTION

Thermal treatment is a promising, environmentally friendly method for the protection of wood that reduces its hygroscopicity and consequently improves its dimensional stability and durability, both of which are needed for outdoor applications (Bourgois and Guyonnet 1988; Tjeerdsma et al. 1998; Militz 2002; Bekhta and Niemz 2003). The important negative aspect of thermal modification is the loss in mass and strength, and the alteration of stiffness, which limit the potential use of thermally treated wood in structural applications.

Timber engineering deals with the evaluation of the load-bearing capacity of structural members in areas connected with mechanical connectors, openings, and notches. The load-bearing safety of structural units is usually acquired on the basis of experimental investigations with subsequent finite element (FE) simulations (Gaff et al. 2015). The numerical data of strength and stiffness of solid wood from several published works (Kollmann and Cote 1968; Dinwoodie 2000; Mackerle 2005) has been reported. In reference to compressive loads, many studies have been conducted on elastic compression mechanisms (Bodig and Jayne 1982; Niemz 1993) and underlying fracture criteria (Daudeville 1999; Mackenzie-Helnwein et al. 2003). Further publications examined the different angles of the grain (Reiterer and Stanzl-Tschegg 2001), and special aspects, such as the impact of temperature, moisture content (Hering et al. 2012; Hering et al. 2013; Ozyhar et al. 2013a), size effects (Schneeweiss 1963; Dill-Langer et al. 2003), creep dependency (Keith 1972), and the strain rate effects (Reid and Peng 1997; Vural and Ravichandran 2003).

Changes and modifications to the wooden components were confirmed after the thermal treatment of wood from previous works (Kollmann and Fengel 1965; Dietrichs et al. 1978; Bourgois and Guyonnet 1988; Yildiz and Gümüskaya 2007) and appear to be involved in the effect of thermal treatment on the general reduction of wood mechanical properties (Kubojima et al. 2000a; Santos 2000; Windeisen et al. 2008; Taghiyari et al. 2012). Consequently, the reexamination of the mechanical properties of thermally treated wood is desired when the material is purposed for construction applications. During compressive loading testing, a slight increase in the compression strength along the grain was reported for poplar, beech, and ash woods after the thermal modification procedure (Windeisen et al. 2008; Taghiyari et al. 2012). The authors contribute the rise in compression strength to the relative increase in lignin content and its condensation, which was confirmed using NIR spectroscopy (Windeisen et al. 2008).

This study was performed to investigate the impact of an industrial thermal treatment process on the behavior of defect-free wood under compression loads. Furthermore, these findings can be used to elaborate on the potential use of thermally-treated wood in the construction sector by researching proper material simulation models.

EXPERIMENTAL

Materials

Ten beech wood boards (Fagus sylvatica L.), 32 mm by 2 m (thickness by length (L)), having no visible defects, were randomly selected from the conditioned warehouse (T = 20 °C; RH = 65%) of an industrial thermal treatment company (Evolen, Novska, Croatia). Selected boards were split into halves (L = 1 m) for the control (C) board samples and thermally-treated board samples (TT). Industrial thermal treatment in an unsaturated steam atmosphere (P_atm = 1.2 bar) was performed at the Evolen company (Croatia) on TT board samples. The treatment included the following phases: a pre-drying phase (T = 105 °C; t = 24 h) and a stepwise heating phase (ΔT = +15 °C/h). Heating at a maximum temperature of 210 °C for 4 h was followed by cooling (ΔT = –15 °C/h) and conditioning (T = 20 °C; RH = 65%). The treatment was regarded as an intensive modification, and offered a compromise between good stability and durability, as well as an assumed decrease in mechanical properties. However, detailed processing data was confidential and thus could not be published.

Two prismatic and oriented compression wood specimens 20 × 20 × 20 mm (longitudinal × radial × tangential) were constructed after the treatment process from each oriented board of unmodified (C) and thermally-treated wood (TT) for the transverse (T) and along the grain (L) uniaxial compression testing.

Methods

Experimental Procedures

Compression wood specimens were conditioned at room temperature (T = 20 ±    0.1 °C) by storing them into a chamber with a saturated salt solution (NaNO₂; RH = 65 ±  1%) to achieve the equilibrium state. Beforehand, the compression test specimens were weighed (Δm = ± 0.001 g) and measured (ΔL = ± 0.01 mm) to determine the density (ρ) of each specimen.

Transverse (T) and longitudinal (L) displacement-controlled compression tests were conducted using a Universal Testing Machine (ZwickZ100, Ulm, Germany) with a load cell with the maximum capacity of 100 kN. The specimens were loaded until failure with a constant loading rate so that the specimen failure was reached in 90 ± 30 sec. The loading rate was adjusted in both tested wood directions (Fig. 1). The stress-strain data was captured at 0.1 s time intervals.

The Young’s modulus of elasticity (MOE) was obtained from the ratio of the stress (σ) to the relative strain (ε) measured in the linear elastic range. The specific stress boundaries σ_i,1 and σ_i,2 were set at 10% and 40% of the specimen strength and adjusted in accordance with the wood direction. The ultimate strength (σ_max) was calculated from the maximum load (F_max) at the point of failure and at the cross sectional area (A) of the unloaded specimen (Fig. 1).

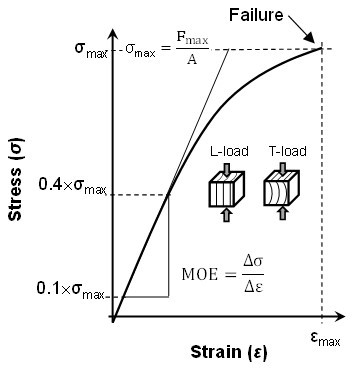
Fig. 1. Principle of loading direction and determination of compression modulus of elasticity and ultimate stress from the stress-strain relationship

Specimens were dried after the compression test in a vacuum drier (T = 50 °C; P = 20 mbar). The gravimetric method was used to determine the moisture content (MC) from the difference between equilibrium (m_e) and oven-dry mass (m₀) of each specimen (SIST EN 13183-1).

Numerical procedures

In case the force-displacement curve consisted of linear and non-linear parts it is not possible to model the test results using Hook’s Law, which applies only for linear elastic materials. In this case it is a possibility to use hyperelastic material models (Constitutive Law) to calibrate the data presented in the form of the experimental force-displacement curve.

Hyperelastic materials are described in terms of a “strain energy potential,” which defines the strain energy stored in the material per unit of reference volume (volume in the initial configuration) as a function of the strain of a single point in the material (Abaqus 2013). Several traditional constitutive hyperelastic models (Yeoh, Ogden, Neo Hooke, Marlow, etc.) were analyzed in this study. Through extensive numerical simulations, Marlow’s constitutive model was chosen as an appropriate model for the data presented in this work.

The form of the strain energy potential per unit of reference volume in the Marlow constitutive model is defined as follows (Abaqus 2013):

where U_dev indicates the deviatoric part, U_vol  stands for the volumetric part,  stands for the first deviatoric strain invariant, and J_el is the elastic volume ratio. The deviatoric part of the potential is defined as either uniaxial, equibiaxial, or planar, depending on the test data, while the volumetric part is defined by the volumetric test data, Poisson’s ratio, or specifying the lateral strains together with the uniaxial, equibiaxial, or planar test data (Abaqus 2013).

The Marlow model was appropriate when only one set of test data was available. In this case, the strain energy potential was constructed so it would fit the test data very accurately. Furthermore, the model covered reasonable behavior in other deformation modes (Abaqus 2013).

Regarding the symmetry of the test samples (a cube with 20 mm long sides), only one quarter of the test samples were modeled with the appropriate symmetry boundary conditions being specified (Fig. 2). The symmetric planes were y-z and x-y. Figure 2 presents the boundary conditions with quasi-static load (displacement) in the direction –y and with the support of the lower surface in the plane x-z, in the direction of the normal y. The model was discretized with 20 noded quadratic hexa elements (Fig. 2c). The presented numerical model adequately described the conditions during the compression test.

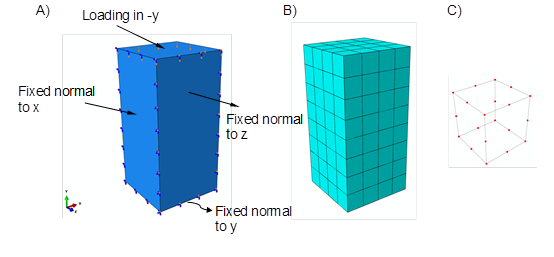
Fig. 2. Finite element model: A) boundary conditions B) discretization of the model, and C) quadratic finite element

RESULTS AND DISCUSSION

The thermal treatment significantly reduced the density of beech wood, determined at a normal climate (∆ρ = –10.3%), from a mean value of 712 kg/m³ to 639 kg/m³ (Fig. 3). The reduction of wood density was expected and confirmed in several studies (Kubojima et al. 2000a; Poncsak et al. 2006), primarily as a consequence of the thermal degradation of wood polyoses (Dietrichs et al. 1978; Bourgois and Guyonnet 1988). However, smaller portion of wood density changes can be attributed to the reduction in the equilibrium moisture content, which was lowered at the tested climate from 7.9% to 3.3% (Fig. 4). Volume shrinkage of 2.0% is namely established by reduced EMC of thermally treated wood (DEMC = -4.6%), when shrinkage coefficients of 0.252 %/% and 0.175 %/% in tangential and radial direction of this material are considered (Firšt et al. 2010). Therefrom the relative wood mass loss of approx. 12% was achieved after the treatment, and even exceeded the reduction of wood density.

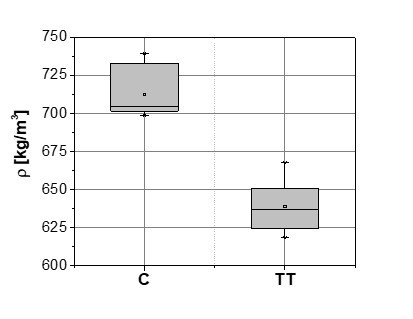
Fig. 3. Wood density (ρ) distribution before (C) and after (TT) the thermal treatment of beech wood

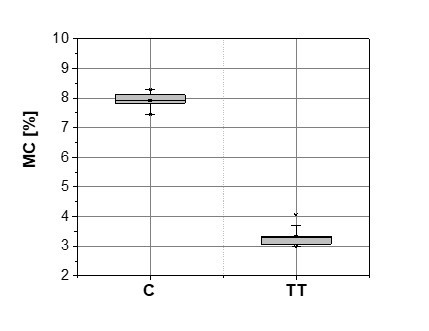
Fig. 4. Moisture content (MC) distribution before (C) and after (TT) the thermal treatment of beech wood

The stiffness of thermally-treated beech wood, determined at a normal climate, was generally increased. The 29.4% increase in mean MOE along the grain was confirmed after the thermal treatment (MOE_L.C = 7.5 GPa; MOE_L.TT = 9.7 GPa). Similarly, the stiffness transverse to the grain (MOE_T.C = 1.8 GPa; MOE_T.TT = 2.1 GPa) increased by 16.2% (Fig. 5). This increase in stiffness is often reported at mild thermal treatment conditions (Kubojima et al. 2000b; Santos 2000), where it is related to the formation of new chemical bonds with higher binding energy than in case of cleaved hydrogen bonds (Rusche 1973). The separate FT-NIR spectroscopic analysis of the same material also confirmed chemical modification of hemicelluloses, amorphous and semi-crystalline cellulose, and lignin (Straže et al. 2013).  However, increased stiffness after thermal treatment might be related to the reduced MC of thermally treated beech wood, since the negative relationship between wood stiffness and moisture content is well known (Borrega and Kärenlampi 2008; Hering et al. 2012; Ozyhar et al. 2013b).

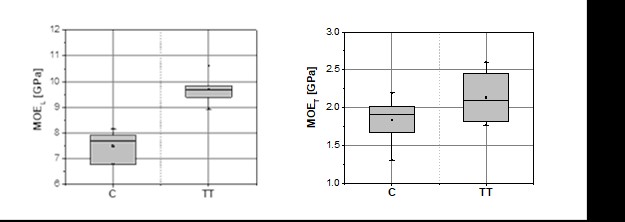
Fig. 5. Longitudinal (left) and transverse stiffness distribution (right) before (C) and after (TT) the thermal treatment of beech wood

The thermal treatment caused alternate changes in the compression strength of beech wood. After the treatment, the ultimate compression strength of beech along the grain increased by 44.8% (σ_max.L.C = 49.7 MPa; σ_max.L.TT = 72.0 MPa), whereas the compression strength transverse to the grain decreased by 24.7% (σ_max.T.C = 10.5 MPa; σ_max.T.TT = 7.9 MPa) (Fig. 6). This slight increase in compression strength along the grain was also found for various wood species after thermal modification; this was explained by the relative increase in lignin content and its condensation after the process (Zaman et al. 2000; Windeisen et al. 2008; Taghiyari et al. 2012). Studies indicate a clear increase in compression strength of thermally-treated wood along the grain, additionally with a lower amount of bound water, which was established also in this research (Boonstra et al. 2007).

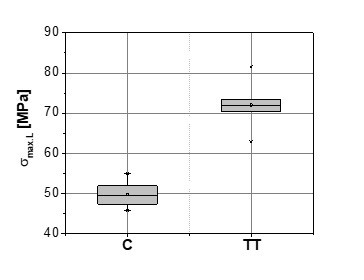
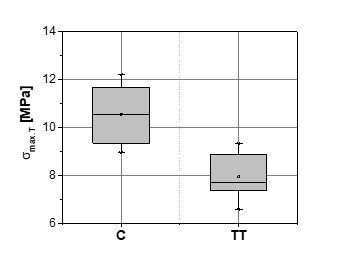
Fig. 6. Longitudinal (left) and transverse ultimate strength distribution (right) before (C) and after (TT) the thermal treatment of beech wood

The compression strength perpendicular to the grain was much lower than the strength parallel to the grain; this might be explained by the presence of weak and soft secondary bonds acting in the transverse direction of the cellulose microfibrils (Winandy and Rowell 1984). The FT-NIR study of this material also confirmed changes of semi-crystalline cellulose regions (Straže et al. 2013). In the transverse direction, the effect of the cellulose microfibrils on the compression strength was limited when compared to the longitudinal direction. Therefore, the assumed degradation of hemicelluloses within the lignin-hemicellulose matrix after the thermal treatment might reduce the load sharing capacity of wood and more prominently effect the compression strength in the transverse direction (Winandy and Rowell 1984; Winandy and Lebow 2001). The decrease in the radial compression strength after thermal treatment might be additionally affected by small radial fissures (Boonstra et al. 2006). 

Numerical Results

Force and displacement were recorded for each compression test and modeled using the finite element method. Therefore each compression test was modeled separately with material response consideration only in one axial plane. Comparison of results for different material models (Marlow, Yeoh, Ogden) are presented in Fig. 7.

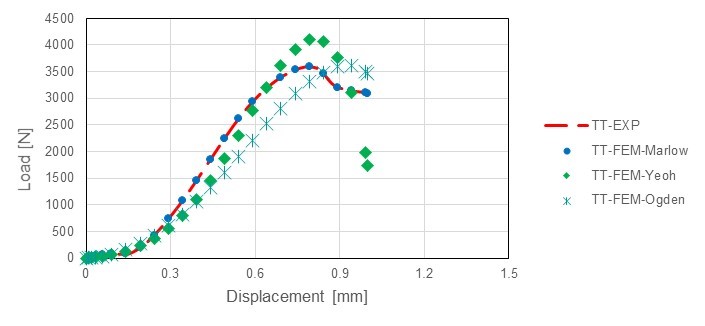
Fig. 7. Comparison between different material models for modelling of compression test for thermally-treated (TT) board samples in the transverse loading direction

Results in Figure 7 show that the Marlow material model was the most appropriate for simulation of presented experimental tests. Therefore it was used for numerical modeling of presented experimental tests.

The comparison between numerical and experimental results is presented in Figs. 8 and 9. It was evident from the results in Fig. 8 that the largest compressive force in the transverse direction was approximately the same for the control (C) and thermally-treated (TT) board samples, whereas the largest compressive forces in the longitudinal direction were approximately 50% larger in thermally-treated (TT) samples than the control (C) samples. The results in Fig. 8 and Fig. 9 also show a favorable alignment between the experimental measured data and computational simulation results. It can be concluded that the Marlow constitutive model was appropriate for computational simulation of the presented problem.

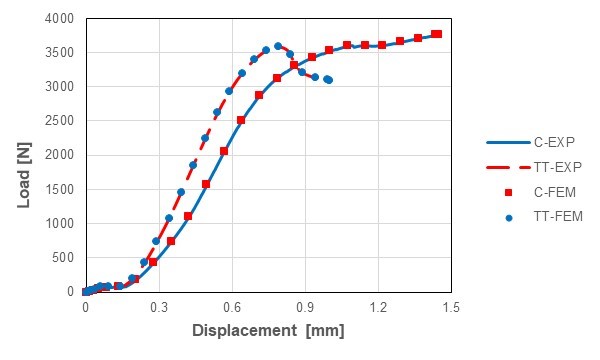
Fig. 8. Comparison between numerical and experimental results for the control (C) and thermally-treated (TT) board samples in the transverse loading direction

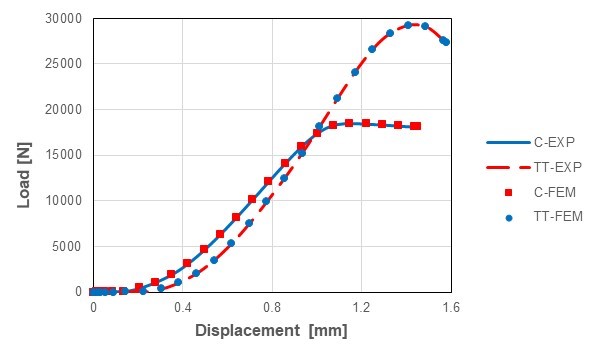
Fig. 9. Comparison between numerical and experimental results for the control (C) and thermally-treated (TT) board samples in the longitudinal loading direction

The presented results apply for cases when forces act in one direction only (either in the longitudinal or transverse direction). Consequently, the use of the presented numerical model is limited, in practice, when loads with components are simultaneously active in both directions – longitudinal and transverse.

CONCLUSIONS

1. The intensive thermal treatment caused notable wood mass loss and a reduction of wood density (10.3%), presumably because of the degradation of wood hemicelluloses. The decreased equilibrium moisture content (∆EMC = –58%) was confirmed at normal climate conditions.
2. After the thermal treatment, the compression modulus of elasticity of beech wood increased by 29.4% along the grain and 16.2% transverse to the grain.
3. Because of the thermal treatment, the ultimate compression strength of beech wood parallel to the grain increased by 44.8% and decreased by 24.7% perpendicular to the grain.
4. The alteration of testing mechanical properties was mostly attributed to the chemical changes of thermally treated wood. Additionally, the impacts of beech wood’s structural anisotropy on strength and stiffness properties were present, combined with differences in EMC of innate and thermally treated wood.
5. It was evident from the experimental results that the largest compressive force in the transverse direction was approximately the same for the control (C) and thermally-treated (TT) board samples, whereas the largest compressive force in the longitudinal direction was approximately 50% larger in thermally-treated (TT) samples than in control (C) samples.
6. In this research, numerical simulations were dealt with separately for loads in the longitudinal and transverse directions. It was established that wood behavior during compression testing can be very accurately described by these two loading directions using the Marlow model for hyperelasticity.

ACKNOWLEDGEMENT

The authors would like to thank the Slovenian Research Agency and Ministry of agriculture, forestry, and food for support of Programme P4-0015, P2-0182, and V4-1419. Thanks also go the Evolen Company (Croatia) for providing timber material for this study.

REFERENCES CITED

Abaqus 6.13. (2013).  “Hyperelasticity,” in: Abaqus Analysis User’s Guide, Dassault Systèmes Simulia Corp, Providence, RI, USA.

Bekhta, P., and Niemz, P. (2003). “Effect of high temperature on the change in color, dimensional stability and mechanical properties of spruce wood,” Holzforschung 57(5), 539-546. DOI: 10.1515/HF.2003.080

Bodig, J., and Jayne, B. (1982). “Determination of mechanical properties,” in: Mechanics of Wood and Wood Composites, Van Nostrand Reinhold Company, New York, USA.

Boonstra, M., Rijsdijk, J. F., Sander, C., Kegel, E. V., Tjeerdsma, B. F., Militz, H., Van Acker, J., and Stevens, M. (2006). “Microstructural and physical aspects of heat treated wood. Part 1. Softwoods,” Maderas Ciencia y Technologia 8(3), 193-208. DOI: 10.4067/S0718-221X2006000300007

Boonstra, M., Van Acker, J., Tjeerdsma, B. F., and Kegel, E.V. (2007). “Strength properties of thermally modified softwoods and its relation to polymeric structural wood constituents,” Annals of Forest Science 64(7), 679-690. DOI: 10.1051/forest:2007048

Borrega, M., and Kärenlampi, P.P. (2008). “Mechanical behaviour of heat-treated spruce (Picea abies) wood at constant moisture content and ambient humidity,” Holz als Roh- und Werkstoff 66(1), 63-69. DOI: 10.1007/s00107-007-0207-3

Bourgois, J., and Guyonnet, R. (1988). “Characterization and analysis of torrified wood,” Wood Science and Technology 22(2), 143-155. DOI: 10.1007/BF00355850

Daudeville, L. (1999). “Fracture in spruce: Experiment and numerical analysis by linear and non linear fracture mechanics,” Holz als Roh- und Werkstoff 57, 425-432. DOI: 10.1007/s001070050068

Dietrichs, H. H., Sinner, M., and Puls, J. (1978). “Potential of steaming hardwoods and straw for feed and food production,” Holzforschung 32(6), 193-199. DOI: 10.1515/hfsg.1978.32.6.193

Dill-Langer, G., Cruz Hidalgo, R., Kun, F., Moreno, Y., Aicher, S., and Herrmann, H. J. (2003). “Size dependency of tension strength in natural fiber composites,” Physica A: Statistical Mechanics and its Applications 325(3-4), 547-560. DOI: 10.1016/S0378-4371(03)00141-9

Dinwoodie, J. M. (2000). “Strength and failure in timber,” in: Timber: Its Nature and Behaviour, Taylor and Francis, New York, USA. DOI: 10.4324/9780203477878

EN 13183-1 “Moisture content of a piece of sawn timber. Part 1: Determination by oven dry method.” European Committee for Standardisation (CEN),  Brussels, 2002, 7 pp.

Firšt, U., Straže, A., and Gorišek, Ž. (2010). “Comparative analyses of sorption isotherms and swelling behaviour of heat treatment and untreated beech, ash, maple and black locust,” in: The 4th Conference on Hardwood Research and Utilisation in Europe 2010, Nemeth, R., and Teischinger, A. (eds.), University of West Hungary Press, Sopron, pp. 148-155.

Gaff, M., Gašparík, M., Borůvka, V., and Babiak, M. (2015). “Simulating stresses associated with the bending of wood using a finite element method,” BioResources 10(2), 2009-2019. DOI: 10.15376/biores.10.2.2009-2019

Hering, S., Keunecke, D., and Niemz, P. (2012). “Moisture-dependent orthotropic elasticity of beech wood,” Wood Science and Technology 46(5), 927-938. DOI: 10.1007/s00226-011-0449-4

Hering, S., Saft, S., Resch, E., Niemz, P., and Kaliske, M. (2013). “Characterisation of moisture-dependent plasticity of beech wood and its application to a multi-surface plasticity model,” Holzforschung 66(3), 373-380. DOI: 10.1515/hf.2011.162

Keith, C. T. (1972). “The mechanical behaviour of wood in longitudinal compression,” Wood Science 4(4), 234-244.

Kollmann, F., and Cote, W. A. (1968). “Mechanics and rheology of wood,” in: Principles of Wood Science and Technology: Solid Wood, Springer-Verlag, Berlin. DOI: 10.1007/978-3-642-87928-9

Kollmann, F., and Fengel, D. (1965). “Änderungen der chemischen Zusamensetzung von Holz durch thermische Behandlung,” Holz als Roh- und Werkstoff 23(12), 461-468. DOI: 10.1007/BF02627217

Kubojima, Y., Okano, T., and Ohta, M. (2000a). “Bending strength and toughness of heat-treated wood,” Journal of Wood Science 46(1), 8-15. DOI: 10.1007/BF00779547

Kubojima, Y., Okano, T., and Ohta, M. (2000b). “Vibrational properties of heat-treated wood,” Journal of Wood Science 46(1), 63-67. DOI: 10.1007/BF00779555

Mackenzie-Helnwein, P., Eberhardsteiner, J., and Mang, H. A. (2003). “A multisurface plasticity model for clear wood and its application to the finite element analysis of structural details,” Computational Mechanics 31(1-2), 204-218. DOI: 10.1007/s00466-003-0423-6

Mackerle, J. (2005). “Finite element analyses in wood research: A bibliography,” Wood Science and Technology 39(7), 579-600. DOI: 10.1007/s00226-005-0026-9

Militz, H. (2002). “Heat treatment of wood: European processes and their background,” in: Internal Research Group on Wood Preservation, Section 4-Processes, No IRG/WP 02-40241, Cardiff, Wales, United Kingdom.

Niemz, P. (1993). “Elastomechanische und rheologische Eigenschaften von Holtz und Holzwerkstoffen,” in: Physik des Holzes und Holz Werkstoffe, DRW-Verlag, Leinfelden-Echterdingen.

Ozyhar, T., Hering, S., and Niemz, P. (2013a). “Moisture-dependent orthotropic tension-compression asymmetry of wood,” Holzforschung 67(4), 395-404. DOI: 10.1515/hf-2012-0089

Ozyhar, T., Hering, S., Sanabria, S. J., and Niemz, P. (2013b). “Determining moisture-dependent characteristics of beech wood by means of ultrasonic waves,” Wood Science and Technology 47(2), 329-341. DOI: 10.1007/s00226-012-0499-2

Poncsak, S., Kocaefe, D., Bouazara, M., and Pichette, A. (2006). “Effect of high temperature treatment on the mechanical properties of birch (Betula papyrifera),” Wood Science and Technology 40(8), 647-663. DOI: 10.1007/s00226-006-0082-9

Reid, S. R., and Peng, C. (1997). “Dynamic uniaxial crushing of wood,” International Journal of Impact Engineering 19(5-6), 531-570. DOI: 10.1016/S0734-743X(97)00016-X

Reiterer, A., and Stanzl-Tschegg, S. E. (2001). “Compressive behaviour of softwood under uniaxial loading at different orientations to the grain,” Mechanics of Materials 33(12), 705-715. DOI: 10.1016/S0167-6636(01)00086-2

Rusche, H. (1973). “Festigkeitseigenschaften von trockenem Holz nach thermischer Behandlung,” Holz als Roh- und Werkstoff 31(7), 273-281. DOI: 10.1007/BF02607297

Santos, J. A. (2000). “Mecanical behaviour of Eucalyptus wood modified by heat,” Wood Science and Technology 34(1), 39-43. DOI: 10.1007/s002260050006

Schneeweiss, G. (1963). “Der Groesseneinfluss im Druckversuch quer zur Faser,” Holzforschung und Holzverwertung 15(6), 125-130

Straže, A., Gorišek, Ž., Pervan, S., Sandak, A., and Sandak, J. (2013). “The sorption properties of some thermally treated hardwoods analysed by thermodynamics, surface fractality and FT-NIR spectroscopy. Characterization of modified wood in relation to wood bonding and coating performance,” 16^th to 18^th October, 2013, Rogla. University of Ljubljana and University of Primorska. pp. 228-237.

Taghiyari, H. R., Enayati, A., and Gholamiyan, H. (2012). “Effects of nano-silver impregnation on brittleness, physical and mechanical properties of heat-treated hardwoods,” Wood Science and Technology 47(3), 467-480. DOI: 10.1007/s00226-012-0506-7

Tjeerdsma, B.F., Boonstra, M., Pizzi, A., Tekely, P., and Militz, H. (1998). “Characterization of thermally modified wood: Molecular reasons for wood performance improvement,” Holz als Roh- und Werkstoff 56(3), 149-153. DOI: 10.1007/s001070050287

Vural, M., and Ravichandran, G. (2003). “Dynamic response and energy dissipation characteristics of balsa wood: Experiment and analysis,” International Journal of Solids and Structures 40(9), 2147-2170. DOI: 10.1016/S0020-7683(03)00057-X

Winandy, J. E., and Lebow, P. K. (2001). “Modelling strength loss in wood by chemical composition. Part I. An individual component model for southern pine,” Wood and Fiber Science 33(2), 239-254.

Winandy, J. E., and Rowell, R. M. (1984). “The chemistry of the wood strength,” in: The Chemistry of Solid Wood, Rowell, R. M. (ed.), American Chemical Society, Washington, DC. DOI: 10.1021/ba-1984-0207.ch005

Windeisen, E., Bächle, H., Zimmer, B., and Wegener, G. (2008). “Relations between chemical changes and mechanical properties of thermally treated wood,” Holzforschung 63(6), 773-778. DOI: 10.1515/HF.2009.084

Yildiz, S., and Gümüskaya, E. (2007). “The effects of thermal modification on crystalline structure of cellulose in soft and hardwood,” Building Environment 42(1), 62-67. DOI: 10.1016/j.buildenv.2005.07.009

Zaman, A., Alen, R. J., Kotilainen, R. (2000). “Heat behaviour of Pinus sylvestris and Betula pendula at 200-230 °C,” Wood and Fiber Science 32(2), 138-143.

Article submitted: June 24, 2015; Peer review completed: October 13, 2015; Revised version received: October 28, 2015; Accepted: November 1, 2015; Published: November 12, 2015.

DOI: 10.15376/biores.11.1.223-234