Dynamic testing of the elastic modulus and shear modulus of full-scale laminated veneer lumber

Huang, Y., Chen, S., Dauletbek, A., Yang, X., Wang, J., Sun, X., Xie, W., and Wang, Z. (2021). "Dynamic testing of the elastic modulus and shear modulus of full-scale laminated veneer lumber," BioResources 16(4), 8273-8288.

Abstract

The feasibility of the dynamic testing was explored for the elastic modulus and shear modulus of full-scale laminated veneer lumber in batches at the production site. In order to do so, dynamic testing and analysis, involving a hammer blow and detection of frequencies, were carried out on the laminated veneer lumber free-plate placed in two ways: suspended and placed on a sponge. The results showed that the mode shape and modal frequency value of the suspended laminated veneer lumber free-plate obtained from the modal test were consistent with those of the specimens placed on the sponge. The elastic modulus and shear modulus values of the laminated veneer lumber free-plate obtained in sponge mode based on the transient excitation method were 3.99% and 3.08% higher than the elastic modulus and shear modulus values of the laminated veneer lumber obtained in suspension mode obtained based on the modal test method. The feasibility and reliability of the elastic modulus and shear modulus values obtained by the laminated veneer lumber free-plate in sponge mode were verified.

Download PDF

Full Article

Dynamic Testing of the Elastic Modulus and Shear Modulus of Full-Scale Laminated Veneer Lumber

Yujie Huang,^a Si Chen,^a Assima Dauletbek,^c Xiaojun Yang,^a Jun Wang,^d Xian`e Sun,^b Wenbo Xie,^a and Zheng Wang ^a,*

Keywords: Laminated veneer lumber; Elastic modulus; Shear modulus; Transient excitation method; Modal test; Free hanging; Sponge supporting

Contact information: a: College of Materials Science and Engineering, Nanjing Forestry University, Nanjing 210037, China; b: Lianyungang Gongliang Wood Products Co., Ltd, Lianyungang 222002, China; c: College of Civil Engineering, Nanjing Forestry University, Nanjing 210037, China; d: College of Computer Science and Technology, Nanjing Forestry University, Nanjing 210037, China;

* Corresponding author: wangzheng63258@163.com

GRAPHICAL ABSTRACT

INTRODUCTION

In the wood processing industry, laminated veneer lumber (LVL) is a widely used engineered structural material. Laminated veneer lumber not only has the natural characteristics of wood, but it also has better mechanical and physical properties, e.g., bending strength, high stiffness, and strong weather resistance, compared to sawn timber. Despite the rapid development of steel structures, natural building materials based on bamboo and wood are deeply favored by users in construction, furniture, interior decoration, transportation, and other industries (Tan and Zhou 2007; Yu et al. 2007; Liu et al. 2007; Zhang et al. 2008; Schweigler et al. 2016; Fu et al. 2019; Ye et al. 2019; Yang et al. 2021; Zhang et al. 2021; Yang et al. 2021). In order to meet the objective needs of various users in LVL products of different quality levels, it is particularly important to carry out online dynamic non-destructive tests of the elastic modulus (E) and shear modulus (G) of LVL and to evaluate the basic research applications for quality grading (Hu et al. 2002; Liang 2008; Cavalli and Togni 2013; Nasir et al. 2019; Wang et al. 2019). Dynamic vibration testing has been commonly and successfully used due to its numerous advantages, e.g., accuracy, speed, simplicity, and high reliability, which yields results that are consistent with the results of the traditional static method (Huang 2008; Gilbert et al. 2017; Hong et al. 2021; Zhang et al. 2021; Zhou et al. 2021). This goes a long way towards enhancing the continuity and efficiency of production.

From 1986 to 1991, Nobuo Sobue measured the modulus of elasticity (MOE) and modulus of rupture (MOR) of wood with different specifications under different constraint conditions (Sobue 1986a,b, 1988, 1991). Sobue used the fast Fourier transformation (FFT) spectrum analysis method to obtain various resonance frequencies of wood and then used Timoshenko’s flexible vibration theory formula to calculate the elastic modulus and shear modulus. These articles analyzed the influence of the clamping position or the supporting position on the vibration frequency of each order and the relationship between the elastic modulus corresponding to each resonance frequency (Sobue 1986a,b, 1988, 1991). Wang et al. (2006) used the transient excitation method to measure the longitudinal elastic modulus (E) and the damping ratio ξ of the strawboard and compared them with the results of the static test method. Their primary conclusion was that the measured longitudinal dynamic E value was 7.83% higher than the static E value (Wang et al. 2006). Xiao et al. (2009) built a non-destructive testing system to dynamically measure the dynamic modulus of elasticity of LVL. The system included an acceleration sensor, a signal conditioning circuit, a peak detection and holding circuit, a digital processing and display circuit, and a single-chip microcomputer. In comparison, the values of the dynamic and static modulus of elasticity, measured by the mechanical testing machine, showed a significant correlation with a coefficient greater than 0.9 (Xiao et al. 2009).

Current experimental research on the elastic modulus and shear modulus of LVL is primarily carried out on small specimens and small batches under laboratory conditions. Although the test results are highly reliable, it is generally impossible to carry out batch testing of large LVL specimens or full-scale LVL products. Based on this, according to the modal theory and free vibration theory, this paper adopted the experimental modal method and the method of free transient excitation to evaluate the accuracy and reliability of E and G dynamic tests on a batch of LVL plate specimens in two different placement modes (Wang et al. 2013, 2014, 2015). The aim of the study was to explore the possibility of full-scale LVL online inspection and its quality grading application work, and laying the foundation for realizing the online inspection of mass LVL product quality in factories, which has good engineering application value.

EXPERIMENTAL

Modal Test Method for the Laminated Veneer Lumber (LVL) Free-Plate in the Suspension Mode

Materials

The 10 pieces of Italian poplar (Populus euramericana cv. ‘I-214’) LVL plates (numbered 1 through 10) had the following characteristics: dimensions of 2700 mm × 770 mm × 30 mm, an average air-dry density (ρ) of 549 kg/m³, and a moisture content (MC) of 12.5%. In addition, 10 pieces of LVL plates (numbered 11 to 20) were manufactured by Guannan Yindelong Wood Industry Co., Ltd, with the following characteristics: dimensions of 2440 mm × 760 mm × 30 mm, an average air-dry density (ρ) of 549 kg/m³, and a MC of 13.0%.

Instruments and accessories

A CRAS dynamic signal acquisition and analysis system, which included an AZ-802 signal conditioning box, AZ-308 signal acquisition box, MaCras mechanical and structural modal analysis software, and PC was purchased, which was manufactured by Nanjing Anzheng Software Engineering Co., Ltd. In addition, a set of free-plate suspension devices, which included a 1 LC1301 hammer (with a mass of 0.35kg and a measuring range of 500N), a LC0501 force sensor with a sensitivity of 4pC/N, was purchased, which was manufactured by Jiangsu Lianneng Electronic Technology Co., Ltd. Two 600 mm × 1200 mm × 150 mm sponge pads, with a density ρ of 45 kg/m³ were purchased, which were produced by Suzhou Tianxin Sponge Factory. In addition, a rubber band was used.

Test method and principle

Based on the dynamic signal vibration test method, the surface of the LVL board was divided into 77 equal points, and each point was tapped in turn to generate lateral free vibration. The mechanical force signal was received through an accelerometer and converted into an analog signal. After signal amplification and low-pass filtering were carried out by the signal conditioning box, the modal parameters and mode shapes of the LVL board specimens were finally obtained through spectrum identification, orthogonal inspection, and other links (Wang et al. 2012). According to Table 7 in GB/T20241-2006, the quality of the specimens were graded. The block diagram of the test system is shown in Fig. 1. In addition, a schematic diagram of how to hitting the LVL free-plate suspended with rubber bands is shown in Fig. 2.

Fig. 1. Block diagram of the test system for the LVL free-plate modal test

Fig. 2. Schematic diagram of how to hitting the LVL free-plate suspended with rubber bands

Placing the test specimens

The LVL specimen was installed on the suspension device with a rubber band to realize a multi-degree-of-freedom linear vibration system. The instruments were connected as shown in Fig. 1, and the accelerometer was placed at the corner of the free-plate (Fig. 3).

Fig. 3. Setup of a free-plate suspension device

Determining the geometric model of the laminated veneer lumber (LVL) specimen by MaCras software

The geometric figure was set as a rectangular parallelepiped with a length of 2700 mm and a width of 770 mm, and the length and width directions were set to 10 equal parts and 6 equal parts, respectively. The geometric model generation diagram and the layout diagram of the 77 equal points are shown in Figs. 4 and 5, respectively.

Parameter settings

The measurement channel was 2, in the Z direction. The total number of geometric nodes was 154, the number of constraint points was 77, and the total number of measurement degrees of freedom was 154.

Testing

Using the hammer excitation method, the running point measurement method, with the accelerometer fixed and the excitation point changed, was used to obtain the frequency response function of the fixed measuring point to each excitation point. The single-input single-output (SISO) frequency response function identification method was adopted, and the modal parameter identification work was completed by fitting the frequency response function curve. Then, the modal measurement was carried out. The analysis frequency was set to 200 Hz, and the FFT was 8192. Before the formal measurement, but after the oscilloscope was qualified, the 77 measurement points were sequentially measured.

Fig. 4. Geometric model of the 154 nodes of the suspended free-plate

Fig. 5. The layout of 77 equal points of the suspended free-plate.

Performing parameter identification to obtain the modal parameters and mode shapes of the specimen

Acquisition of the curve spectrum was performed through initial estimation, and then proceeded through the following stages: gradually completion of the curve fitting, processing of the measurement direction and constraint equation, modal mode normalization and modal orthogonality test procedures, and finally the acquisition of the modal parameters and mode shapes of the LVL specimen.

Transient Excitation Test Method of the LVL Free-Plate Sponge Mode

Material and equipment

Same as the materials and equipment outlined above. The test methods and principles also are the same as outlined above.

Main test steps

First, the LVL was placed on the sponge, as shown in Figs. 6 and 7. The parameters for the system were as follows: the FFT length was 8192, the analysis frequency was 200 Hz, and the voltage range was 5000 mV, which ran freely. The accelerometer was installed on the corner of the LVL test piece, and the corner of the test piece was hit with a hammer. The electrical signal was amplified and filtered through the signal conditioning box and then input to the signal acquisition box. The spectrum of the free-plate specimen was obtained through A/D conversion, and the first-order torsion frequency f_t and the first-order bending frequency f₁ were read. The schematic diagram of how to hitting the LVL free-plate placed on sponge is shown in Fig. 8.

Fig. 6. Schematic diagram of the free-plate placed on the sponge

Fig. 7. Schematic diagram of the free-plate placed on the sponge

Fig. 8. The schematic diagram of how to hitting the LVL free-plate placed on sponge

In order to realize the accuracy and reliability of the E and G values of the LVL plates measured on-site, both sets of LVL plates, i.e., 10 LVL plates (2700 mm × 770 mm × 30 mm) and all 10 LVL plates (2440 mm × 760 mm × 30 mm), were measured in this section.

Transient Excitation Test Method for Laminated Veneer Lumber (LVL) Free-Plate in Suspension Mode

The test materials and instruments, test methods, and principles were the same as previously outlined. The LVL free-plate specimen was suspended with rubber bands. The test system is shown in Fig. 2. The main test steps were the same as outlined above in the Transient Excitation Test Method section. Both sets of LVL plates, i.e., 10 LVL plates (2700 mm × 770 mm × 30 mm) and all 10 LVL plates (2440 mm × 760 mm × 30 mm), were measured in this section.

Modal Test Method for the Laminated Veneer Lumber (LVL) Free-Plate in Sponge Mode

In order to verify the accuracy and reliability of the modal test in suspension mode for the LVL and carry out on-site batch testing of the E and G values of the LVL, it was necessary to conduct modal tests and comparative analysis on the LVL free-plate in sponge mode.

Test method and principle

Same as the test methods and principles outlined above.

Main test steps

The LVL was placed on the sponge pad to realize a multi-degree-of-freedom linear vibration system. The schematic diagram is shown in Figs. 9 and 10. The physical diagram is shown in Fig. 11. The test steps are the same as outlined above in the Transient Excitation Test Method section.

Fig. 9. Joint geometry model of the LVL board placed on the sponge

Fig. 10. Arrangement of the 77 equal points of the LVL board placed on the sponge

Fig. 11. Modal test site of the LVL free-plate placed on the sponge

RESULTS AND DISCUSSION

Theoretical Calculation Formula of the Elastic Modulus (E) and the Shear Modulus (G) of the Test Specimens

According to the beam transverse bending theory, the relationship between its elastic modulus E and the first-order bending frequency (f₁) is shown in Eq. 1,

(1)

where E is the elastic modulus of the specimen (Pa), ρ is the average air-dry density of the specimen (kg/m³), f₁ is the first-order bending frequency (Hz), l is the length of the specimen (m), and h is the thickness of the specimen (m) (Timoshenko 1965)).

The relationship between the first-order torsion frequency f_t of the free-plate and the shear modulus G of the specimen is shown in Eq. 2,

(2)

where G is the shear modulus of the specimen (Pa), l is the length of the specimen (m), b is the width of the specimen (m), h is the thickness of the specimen (m), f_t is the first-order torsional frequency (Hz), ρ is the average air-dry density of the specimen (kg/m³), β = 1/16(16/3-3.36 h/b(1-h⁴/12b⁴ )), γ is the free-plate mode coefficient (γ = 7.4539(1-0.1187 b/l + 0.6013 b²/l²– 0.3824 b³/l³)), r = 0.99998, n = 6, and the applicable aspect ratio of free-plate is l/b = 2 to 8 (Xia et al. 2013).

Modal Test Results and Analysis of the Free-Plate Suspension and Sponge Mode

It can be seen from Table 1 that the first two-order modal frequencies measured under the No. 1 LVL free-plate suspension mode were 16.42 Hz and 19.24 Hz, respectively. They correspond to the first-order torsional mode and the first-order bending mode, as shown in Figs. 12 and 13 (Lv and Xu 2001).

Fig. 12. The first-order torsional mode of the free-plate

Fig. 13. The first-order bending mode of the free-plate

Table 1. The First 10 Modal Frequencies and Damping Values of the Laminated Veneer Lumber (LVL) Free-Plate in Suspension Mode

The modal damping ratio is one of the dynamic characteristics of the structure, which is the damping value under different modal frequencies. For wood materials in an elastic state, the modal damping ratio is within 17%. Obviously, from the modal frequencies of the LVL sheet obtained in Table 1 and the corresponding damping ratio, the LVL sheet specimen is in an elastic state.

Table 2 shows that the first two-order modal frequencies measured under the No. 1 LVL free-plate in the sponge mode were 17.13 Hz and 20.06 Hz, respectively. The vibration modes corresponding to the first-order torsional mode and the first-order bending mode are shown in Fig. 14 and Fig. 15, respectively.

Table 2. The Frequency and Damping Value of the First 10 Modes of the Laminated Veneer Lumber (LVL) Free-Plate in Sponge Mode

Fig. 14. Vibration shape of the first-order torsional mode

Fig. 15. Vibration shape of the first-order bending mode

Obviously, the structural mode of the LVL free-plate in sponge mode was consistent with the results of the first second-order mode and its mode frequency value in suspension mode. The first two-order modal frequencies corresponded to the first-order torsion frequency and the first-order bending frequency, respectively. The LVL elastic modulus (E) and shear modulus (G) values measured under the LVL suspension mode were 8.83% and 8.71% smaller than the E and G values in the sponge mode. Therefore, the E and G values of the LVL free-plate in sponge mode, calculated based on the modal test method, can be regarded as equivalent to the E and G values obtained in suspension mode.

Test Results and Analysis of the Transient Excitation Method in Free-Plate Suspension and Sponge Mode

According to the spectrograms (as shown in Figs. 16 and 17) of the No. 1 test piece and Eqs. 1 and 2, a comparison table of its measurement and calculation was obtained (as shown in Table 3).

Fig. 16. Free-plate frequency spectrum in suspension mode

Fig. 17. Free-plate frequency spectrum in sponge mode

Table 3. Comparison Table of the Test Results of the Free-Plate in Suspension and Sponge Mode

Table 3 shows that the LVL elastic modulus E and shear modulus G values measured in suspension mode were 3.99% and 3.08% smaller than the E and G values in sponge mode, respectively. Combined with the analysis of the results above, it is clear that the No. 1 LVL specimen can be used to measure the E and G values of the LVL free rectangular plate placed on the sponge on site.

To investigate whether the results of the 10 LVL specimens for each of the two specifications can be performed on site for the large-scale dynamic detection of E and G, it was necessary to analyze the correlation between the E and G values of the LVL free-plate in the suspension and sponge modes based on the transient excitation method. According to the calculation results, the test values of the LVL free-plate in sponge mode were consistent with the test results of the LVL free-plate in suspension mode. The former calculated that the E and G values of the 10 2700 mm × 770 mm × 30 mm LVL panels were 3.98% and 5.87% lower than the E and G values of the latter, respectively. The former calculated that the E and G values of the 10 2440 mm × 760 mm × 30 mm LVL panels were 2.59% and 7.09% lower than the E and G values of the latter, respectively.

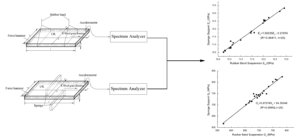
As shown in Figs. 18 and 19, the correlation coefficients (R²) of E and G of the LVL samples tested in two modes were 0.984 and 0.973, respectively, which demonstrates a strong correlation. It was verified that the transient excitation method can be used on the production site to batch-test the E and G values of the LVL plate in sponge mode, which will help improve the quality control work and technical level of quality grading of LVL products (Wang and Ghanem 2021).

Fig. 18. The E correlation diagram in sponge mode and suspension mode

Fig. 19. The G correlation diagram in sponge mode and suspension mode

CONCLUSIONS

The modal tests of the laminated veneer lumber (LVL) free-plate in suspension mode and in sponge mode showed consistent results for the mode shape and modal frequency value. The first second-order modal frequencies corresponded to its first-order torsion frequency and first-order bending frequency, respectively.
The elastic modulus (E) and shear modulus (G) values of the LVL free-plate in sponge mode obtained based on the transient excitation method were 3.99% and 3.08% higher than the E and G values obtained in suspension mode based on the modal test method.
Using the transient excitation method, combined with the measurement results under the free-plate suspension mode, this paper verified the feasibility and reliability of the E and G values obtained by the LVL free-plate in sponge mode, which has high practical application value. The former calculated that the E and G values of the 10 2700 mm × 770 mm × 30 mm LVL panels were 3.98% and 5.87% lower than the E and G values of the latter, respectively. The former calculated that the E and G values of the 10 2440 mm × 760 mm × 30 mm LVL panels were 2.59% and 7.09% lower than the E and G values of the latter, respectively.
This study allows for the dynamic determination of the E and G values of LVL products in batches with high accuracy and reliability. The results are feasible and reliable for practical engineering work, e.g., dynamic online detection and quality grading of LVL products. This method effectively improves the optimal design and content of LVL product technological processes, and the level of its added value is notable.

ACKNOWLEDGMENTS

The authors are grateful for the support of the 2020 Jiangsu Provincial Department of Science and Technology Policy Guidance Program “Italian poplar LVS Structural Plywood Key Process Technology and Equipment Research and Industrialization” project (SZ-LYG2020016), and the 2021 Jiangsu Provincial Agricultural Science and Technology Independent Innovation Fund Project “R&D of key technologies and equipment for online dynamic non-destructive testing and quality grading of straw boards” (CX[21]3049).

REFERENCES CITED

Cavalli, A., and Togni, M. (2013). “How to improve the on-site MOE assessment of old timber beams combining NDT and visual strength grading,” Nondestructive Testing Communications 28(3), 252-262. DOI: 10.1080/10589759.2013.764424

Fu, H., Ding, Y., Wang, Z., Xu, B., and Li, Y. (2019).“Optimal design and application of laminated veneer lumber components for wooden composite doors,” Chinese Journal of Wood Science and Technology 33(4), 54-57. DOI: 10.19455/j.mcgy.20190413

Gilbert, B. P., Bailleres, H., Zhang, H., and McGavin, R. L. (2017). “Strength modelling of laminated veneer lumber (LVL) beams,” Construction and Building Materials 149(11), 763-777. DOI: 10.1016/j.conbuildmat.2017.05.153

Hong, C., Li H., Xiong Z., Lorenzo, R., Li, X., and Wang, Z. (2021). “Axial compressive behavior of laminated bamboo columns with a chamfered section,” Structures 33, 678-692. DOI: 10.1016/j.istruc.2021.04.083

Hu, Y., Gu, J., and Wang, F. (2002). “Developments and prospects in the research on nondestructive testing of physical and mechanical properties of wood and wood composites,” World Forestry Research 15(4), 39-46. DOI: 10.13348/j.cnki.sjlyyj.2002.04.007

Huang, S. (2008). Study on Processing Technology of Strengthened LVL from Plantation Chinese Fir, Master’s Thesis, Beijing Forestry University, Beijing, China.

Liang, S., Wang, X., Cai, Z., Ross, R. J., Allison, R. B., and Fu, F. (2008). “Elastic wave tomography in standing tree decay detection,” Scientia Silvae Sinicae 44(5), 109-114. DOI: 10.11707/j.1001-7488.20080521

Liu, H., Liu, J., and Chai, Y. (2007). “The effect of different factors on MOE and MOR of strengthened bamboo/wood composite LVL,” China Forest Products Industry 49(1), 21-23. DOI: 10.19531/j.issn1001-5299.2007.01.010

Lv, Z., and Xu, J. (2001).“Indentification method of dynamic natural frequencies and damping for large-scale structure,” Journal of Mechanical Engineering 12(6), 72-75+81.

Nasir, V., Nourian, S., Avramidis S., and Cool, J. (2019). “Stress wave evaluation by accelerometer and acoustic emission sensor for thermally modified wood classification using three types of neural networks,” European Journal of Wood and Wood Products 77(1), 45-55. DOI: 10.1007/s00107-018-1373-1

Peng, Y., Wang, Z., and Ai, X. (2018).“Wind-induced fragility assessment of urban trees with structural uncertainties,” Wind & Structures 26(1), 45-56. DOI: 10.12989/was.2018.26.1.045

Schweigler, M., Bader, T. K., Horchreiner, G., Unger, G., and Eberhardsteiner, J. (2016). “Load-to-grain angle dependence of the embedment behavior of dowel-type fasteners in laminated veneer lumber,” Construction and Building Materials 126, 1020-1033. DOI: 10.1016/j.conbuildmat.2016.09.051

Sobue, N. (1986a). “Measurement of Young’s modulus by the transient longitudinal vibration of wooden beams using a fast fourier transformation spectrum analyzer,” Mokuzai Gakkaishi 32(9), 744-747.

Sobue, N. (1986b). “Instantaneous measurement of elastic constants by analysis of the tap tone of wood: Application to flexural vibration of beams,”Mokuzai Gakkaishi 32(4), 274-279.

Sobue, N. (1988).“Simultaneous determination of Young’s modulus and shear modulus of structural lumber by complex vibrations of bending and twisting,” Mokuzai Gakkaishi 34(8), 652-657.

Sobue, N., and Kitazumi, M. (1991). “Identification of power spectrum peaks of vibrating completely-free wood plates and moduli of elasticity measurements,” Mokuzai Gakkaishi 37(1), 9-15.

Tan, S., and Zhou, D. (2007). Wood Industry Handbook, China Forestry Publishing House, Beijing, China.

Timoshenko, S. (1965). Mechanical vibrational science. China Machine Press, Beijing, China.

Wang, Z., Li, L., Yang, J., and Rao, X. (2006).“Measuration and study to elasticity model and damp ratio of the wheat straw board with dynamic and static testing method,” Forestry Science & Technology 18(5), 48-50.

Wang, Z., Li, L., and Gong, M. (2012). “Dynamic modulus of elasticity nad damping ratio of wood-based composites using a cantileverbeam vibration technique,” Construction & Building Materials 28(1), 831-834. DOI: 10.1016/j.conbuildmat.2011.09.001

Wang, Z., Wang, Z., Wang, B. J., Wang, Y., Liu, B., Rao, X., Wei, P., and Yang, Y. (2014). “Dynamic testing and evaluation of modulus of elasticity (MOE) of SPF dimension lumber,” BioResources 9(3), 3869-3882. DOI: 10.15376/biores.9.3.3869-3882

Wang, Z., Gao, Z., Wang, Y., Cao, Y., Wang, G., Liu, B., and Wang, Z. (2015). “A new dynamic testing method for elastic, shear modulus and Poisson’sratio of concrete,” Construction and Building Materials 100, 129-135. DOI: 10.1016/j.conbuildmat.2015.09.060

Wang, Z., Wang, Y., Cao, Y., and Wang, Z. (2016). “Measurement of shear modulus of materials based on the torsional mode of cantilever plate,” Construction and Building Materials 124, 1059-1071. DOI: 10.1016/j.conbuildmat.2016.08.104

Wang, Z., Xie, W., Wang, Z., and Cao, Y. (2018). “Strain method for synchronous dynamic measurement of elastic, shear modulus and Poisson’s ratio of wood and wood composites,” Construction and Building Materials 182, 608-619. DOI: 10.1016/j.conbuildmat.2018.06.139

Wang, Z., Xie, W., Lu, Y., Li, H., and Wang, Z. (2019). “Dynamic and static testing methods for shear modulus of oriented strand board,” Construction and Building Materials 216, 542-551. DOI: 10.1016/j.conbuildmat.2019.05.004

Wang, Z., and Ghanem, R. (2021). “An extended polynomial chaos expansion for PDF characterization and variation with aleatory and epistemic uncertainties,” Computer Methods in Applied Mechanics and Engineering 382, 113854. DOI: 10.1016/j.cma.2021.113854

Xia, T., Liu, W., and Lu, Z. (2013). “The analysis of the influence of ACM spot for whole body first- order torsional mode,” Automotive Technology 40(5), 46-50.

Xiao, J., Yang, J., Sa, C., and Li, C. (2009). “Nondestructive testing of MOE of LVL based on single-chip microcomputer,” China Forest Products Industry 36(5), 19-21+29. DOI: 10.19531/j.issn1001-5299.2009.05.008

Yang, R., Li, H., Lorenzo, R., Sun, Y., and Ashraf, M. (2021). “Flexural behaviour of steel timber composite (STC) beams,” Steel and Composite Structures 41(2), 193-207. DOI: 10.12989/scs.2021.41.2.193

Yang, D., Li H., Wei, D., Lorenzo, R., Corbi, I., Corbi, O., Yuan, C., and Hong, C. (2021). “Length effect on bending properties and evaluation of shear modulus of parallel bamboo strand lumber,” European Journal of Wood and Wood Products 79(6), 1507-1517. DOI: 10.1007/s00107-021-01714-1

Ye, Y., Xu, W., Huang, Q., Chen, C., and Tang, X. (2019). “Effect of veneer thickness on mechanical properties of small-diameter teak laminated veneer lumber,” China Forest Products Industry 56(9), 6-10. DOI: 10.19531/j.issn1001-5299.201909002

Yu, Y., Yu, W., and Wang, G. (2007). “Manufacturing technology and main properties for laminated veneer lumber of eucalyptus,” Scientia Silvae Sinicae 43(8), 154-158.

Zhang, D., Lin, L., Wang, C., Yan, C., Xu, L., and Tang, W. (2008). “Larch LVL for wood structure building production craft and function evaluation,” Forestry Machinery & Woodworking Equipment 36(2), 44-46.

Zhang, H., Li, H., Li, Y., Xiong, Z., Zhang, N., Lorenzo, R., and Ashraf, M. (2021). “Effect of nodes on mechanical properties and microstructure of laminated bamboo units,” Construction and Building Materials 304, 124427. DOI: 10.1016/j.conbuildmat.2021.124427

Zhang, H., Li, H., Hong C., Ziong, Z., Lorenzo, R., Corbi, I., and Ottavia, C. (2021). “Size effect on the compressive strength of laminated bamboo lumber,” Journal of Materials in Civil Engineering ASCE 33(7), 1-12. DOI: 10.1061/(ASCE)MT.1943-5533.0003776

Article submitted: September 2, 2021; Peer review completed: October 9, 2021; Revised version received and accepted: October 23, 2021; Published: October 26, 2021.

DOI: 10.15376/biores.16.4.8273-8288