Abstract
There is a need to understand the effect of wood particle size, as it affects the characteristics of wood-based composites. This study considers the effect of wood particle size relative to the dynamic behavior of wood composites. The compression Split Hopkinson Pressure Bar (SHPB) was introduced to execute dynamic compression testing at the strain rate of 650 s-1, 900 s-1, and 1100 s-1, whereas a conventional universal testing machine (UTM) was used to perform static compression testing at the strain rate of 0.1 s-1, 0.01 s-1, and 0.001 s-1 for four different particle sizes (63 µm, 125 µm, 250 µm, and 500 µm). The results showed that mechanical properties of composites were positively affected by the particle sizes, where the smallest particle size gave the highest values compared to the others. Moreover, the particle size also affected the rate sensitivity and the thermal activation volume of sawdust/HDPE, where smaller particles resulted in lower rate sensitivity. For the post-damage analysis, the applied strain rates influenced deformation behavior differently for all particle sizes of the specimens. In a fractographic analysis under dynamic loading, the composites with large particles experienced severe catastrophic deformation and damages compared to the smaller particles.
Download PDF
Full Article
Effect of Particle Size on Mechanical Properties of Sawdust-High Density Polyethylene Composites under Various Strain Rates
Haliza Jaya,a Mohd Firdaus Omar,a,b* Hazizan Md Akil,c Zainal Arifin Ahmad,c and Nik Noriman Zulkepli a,b
There is a need to understand the effect of wood particle size, as it affects the characteristics of wood-based composites. This study considers the effect of wood particle size relative to the dynamic behavior of wood composites. The compression Split Hopkinson Pressure Bar (SHPB) was introduced to execute dynamic compression testing at the strain rate of 650 s-1, 900 s-1, and 1100 s-1, whereas a conventional universal testing machine (UTM) was used to perform static compression testing at the strain rate of 0.1 s-1, 0.01 s-1, and 0.001 s-1 for four different particle sizes (63 µm, 125 µm, 250 µm, and 500 µm). The results showed that mechanical properties of composites were positively affected by the particle sizes, where the smallest particle size gave the highest values compared to the others. Moreover, the particle size also affected the rate sensitivity and the thermal activation volume of sawdust/HDPE, where smaller particles resulted in lower rate sensitivity. For the post-damage analysis, the applied strain rates influenced deformation behavior differently for all particle sizes of the specimens. In a fractographic analysis under dynamic loading, the composites with large particles experienced severe catastrophic deformation and damages compared to the smaller particles.
Keywords: Wood composite; Particle sizes effect; Dynamic loading; Split Hopkinson pressure bar
Contact information: a: Centre of Excellence Geopolymer and Green Technology (CEGeoGTech), Universiti Malaysia Perlis, Kompleks Pengajian Jejawi 2, 02600 Arau, Perlis; b: School of Materials Engineering, Universiti Malaysia Perlis, Kompleks Pengajian Jejawi 2, 02600 Arau, Perlis; c: School of Material and Mineral Resource Engineering, Universiti Sains Malaysia, 14300, Nibong Tebal, Pulau Pinang, Malaysia;
* Corresponding author: firdausomar@unimap.edu.my
INTRODUCTION
Biocomposites are some of the most advanced and adaptable engineering materials. They can be developed with minimal overall production cost by embedding waste wood particles from other manufacturing processes or recycled materials in polymer. One of the most commonly used wood-derived fillers is wood flour. Wood flour is commercially produced from post-industrial sources, such as planer shavings and sawdust. Wood-derived fillers possess several advantages compared with inorganic fillers, including lower density, greater deformability, eco-friendly, lower abrasiveness, and lower cost (Rahman et al. 2010).
One of the variables distinguishing wood flour is mesh size (particle size). The effect of particle size on the mechanical performance of composites has been addressed by many authors. Particle size greatly influences the mechanical properties of polymeric composites, such as Young’s modulus, yielding stress, fracture toughness, etc. (Hossain et al. 2014). Polymer composites containing particles with a small aspect ratio have also been studied extensively due to their technological and scientific importance (Fu et al. 2008). Composites that had a low aspect ratio showed superior strength, which allows better transfer between the matrix and the fillers (Ashori and Nourbakhsh 2009). Moreover, some researchers concluded on the basis of an energy debonding criterion damage dissipation is strongly dependent on the size of particles, where smaller particles are favorable to increase material toughness (Lauke 2009). Meanwhile, at the same particle content, smaller particle size leads to lower interparticle distance where extensive plastic deformation in the matrix can be easily induced (Zhang et al. 2011).
However, the majority of previous studies only focused on the static behavior without addressing the dynamic mechanical properties of this kind of composite. Many engineering products, and especially composite structures, need to be able to resist high-impact conditions. Therefore, it is critical to determine their dynamic behaviors (e.g. dynamic deformation) in order to avoid any unexpected failure during the service. For example, damage can occur from a hammer being dropped on a composite pipe or from a bullet striking composite armor. Since impact damage resistance is such an important property for composite materials, the desire to produce products or structures that are capable of withstanding high-velocity impacts become even more essential.
In this study, the effect of particle size on the static and dynamic compression properties of sawdust/HDPE composites under various levels of strain rates was examined. In the experimental set-up, a compression split Hopkinson pressure bar (SHPB) apparatus was used to execute high strain rate testing. A universal testing machine (UTM) was used to perform static compression testing of sawdust/HDPE composites using four different sizes of sawdust particles (500 µm, 250 µm, 125 µm, and 63 µm). The size of the sawdust particles was confirmed using a particle size analyzer. Furthermore, composite responses were investigated in terms of their stress/strain behavior, ultimate strength, and stiffness. A correlation between the sawdust particle size, rate sensitivity, and thermal activation volume was also determined. For post-damage analysis, physical observation and scanning electron microscopy (SEM) analysis further clarified the condition of failure for all tested specimens under both static and dynamic loadings.
EXPERIMENTAL
Materials and Fabrication of Composites
High density polyethylene (HDPE) was obtained from ADV System Technology, (Kedah, Malaysia) at 2.0 g/10 min melt flow index (2.16 Kg/190 °C) with the density of 0.9537 g/cm³. Sawdust was obtained from a furniture supplier at Kangar, Perlis, Malaysia, where the initial size is mixed between large and fine particles. The sawdust is from the main species of Sapotaceae, which is also known as Lalaquium spp. (called as nyatoh in Malaysia) and is a light hardwood type. In this study, the automatic hammer continuous grinder (KH-08B) was used to reduce the particle sizes. After that, the sawdust was sieved into four different sizes (i.e. approximately 500 µm, 250 µm, 125 µm, and 63 µm) using a vibratory sieve shaker AS 200 control before sending to the particle size analyzer for particle size confirmation. The HDPE sawdust filler-reinforced composites were prepared by the melt extrusion method. For standardization, 15 wt.% by weight of sawdust was added into the HDPE matrix. A molten sample was taken from the extrusion end, and it was compressed by hot compression molding using a cylinder mold.
Particle Size Analysis
This analysis was purposely run in order to measure the particle size distribution of the sawdust filler. The particle size distribution of micro-sawdust particles was measured by the dry sieving method using dry laser diffraction (Malvern Sciro2000 Mastersizer, Perlis, Malaysia). This approach was employed in order to report the central point of the distribution and to describe the width of distribution. In the case of a symmetric distribution, all central values are equivalent: mean = median = mode. The mean diameters and particle size distribution were computed [D (v, 0.5)], where D and (v, 0.5) are particle size diameter and median for a volume distribution, respectively.
Post Damage Analysis
Scanning electron microscopy (SEM)
The dynamic fracture of sawdust/HDPE composites was examined using SEM (JEOL JSM-6460LA, Penang, Malaysia). Each sample was prepared from a cross section of fracture surfaces, which was attached to an aluminum mount with carbon double-sided tape and sputter-coated with Au/Pd by using a Palaron SC 515 (Penang) to eliminate the electron charging effect.
Mechanical Tests
Static test
In static testing, the slenderness ratio (l/d) of each compression specimen had a dramatic influence on the frictional effects. In this situation, the ASTM E9-89 (1995) standard was highly recommended for the slenderness ratio of polymeric materials. Therefore, the specimen length was cut based on ASTM Designation E9-89, where the slenderness ratio (d = 12 mm) of the specimen was approximately 1.5. Sawdust/HDPE composites were tested under constant crosshead speeds of 1.08 mm/min, 10.8 mm/min, and 108 mm/min, which corresponded to the strain rates of 0.001 s-1, 0.01 s-1, and 0.1 s-1, respectively, using the UTM. To reduce frictional effects during the test, petroleum jelly was applied to both specimen surfaces. Five measurements were taken for each different loading to compute the average behavior of tested composites.
Dynamic test
This test was done using the compression SHPB apparatus (Fig. 1). The system consisted principally of a gun barrel, a 152 mm striker bar, a 1500 mm input bar, and a 1500 mm output bar, which remained elastic during the tests. High strength silver steel was used in the Hopkinson bars to reduce any drastic impedance mismatch between the specimen and the metallic bars (Nakai and Yokoyama 2008).
The specimen was held in place between the two Hopkinson bars (Fig. 1) by applying a small pre-compression load and by turning the head of the support block. In this test, petroleum jelly was also applied to the bar/specimen interfaces to minimize frictional effects.
A Lagrangian x-t diagram showing the details of the strain pulse propagation in the Hopkinson bars is given in Fig. 2. All three strain pulses—incident, reflected, and transmitted—were recorded with two pairs of strain gauges mounted on the Hopkinson bars.

Fig. 1. Schematic diagram of the split Hopkinson pressure bar apparatus
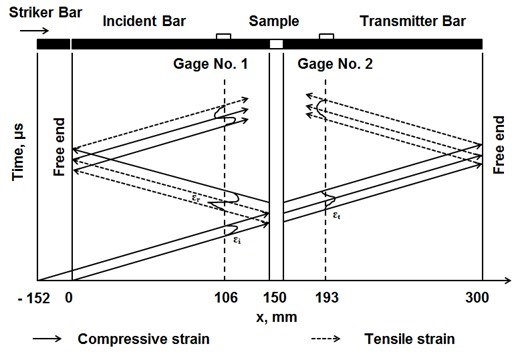
Fig. 2. Lagrangian x-t diagram visualizing wave passage in split Hopkinson bars
The stress (σ), strain (ɛ), and strain rate (έ) of the specimen were determined with the following equations (Omar et al. 2012):
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
where A, E, and c = E/ρ1/2 (ρ = mass density of bar), are cross-sectional area, Young’s modulus, and wave velocity of the bars, respectively. L and As refer to the length and cross-sectional area of the sample, respectively, and the parameters ɛr (t) and ɛt (t) are the collected axial strains of the reflected pulse and transmitted pulse, respectively.
RESULTS AND DISCUSSION
Particle Size Confirmation
Particle size was measured with a size analyser, and the particle shapes were examined using the SEM. Figure 3 shows the cumulative results and the SEM images of four different sizes of sawdust particles. The mean particle sizes of the four sets of sawdust particles were 500 μm, 250 μm, 125 µm, and 63 µm. SEM images were used to identify the particle shapes. The sawdust particles had different shapes, such as cylindrical and spherical, which could both be referred to as irregular shapes (Lu et al. 2010). Thus, the sawdust particles were appropriately sized and shaped. Apart from that, aspect ratio also is one of the important parameters that need to be considered in evaluating the effect of particle size and shape towards composite’s mechanical properties. Theoretically, aspect ratio can be defined as the length of the longest Feret diameter over the length of the shortest Feret diameter [Flongest/Fshortest] (Moschakis et al. 2005) where it has been implemented to sawdust filler as illustrated in Fig. 4. Based on the SEM images in Fig. 3, it was experimentally demonstrated that the aspect ratio of irregular cellulosic sawdust filler used in this study was approximately 3.

Fig. 3. The particle size distribution results (a-d) and SEM images of sawdust microparticles on sawdust/HDPE composites
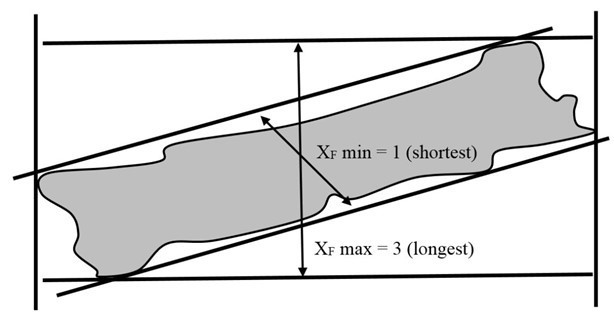
Fig. 4. The determination of aspect ratio for sawdust particles
Stress/strain Characteristics
By recording the amount of deformation (strain) at distinct intervals of compression (stress), many of the material characteristics may be calculated, including yield strength, stiffness, ultimate strength, and fracture (Beer et al. 2001). Therefore, the true compression stress/strain curves of the sawdust/HDPE composites were summarized as a function of filler measured under various loading rates (Fig. 5).
The stress/strain curves of neat HDPE under similar loading rates have been reported previously (Jaya et al. 2016). All sawdust/HDPE composites behaved differently under various loadings, where failure points were examined under dynamic but not static loading. As the strain rate increased, the molecular mobility of the polymer chains decreased; therefore, more fractures developed to acclimate to a larger deformation of specimens (Guo and Li 2007). Moreover, the specimens were subjected with high velocities, which directly contributed to severe catastrophic shear yielding and micro-damage within specimens.
Additionally, the particle sizes had a noticeable influence on the stress/strain mechanical properties of all tested specimens, mainly under high strain rate. At high strain rate loading, composites with smaller particles (125 µm and 63 µm) showed a more significant strain-hardening than composites with larger particles (250 µm and 500 µm). This outcome shows that the particle sizes directly affected the toughness behavior of the composites, as a particle with smaller size tend to have larger surface area, which directly acts as the adhesive factor towards the composite system.
Theoretically, an increase in debonding stress as the particle size decreases would create an adhesive agent that will eventually decrease the toughening effect (Dubnikova et al. 2004). Moreover, according to Kitey and Tippur (2005), filler particle size influences the fracture and cracking behavior when particles are weakly bonded to the matrix. Based on this concern, a failure mechanism under compressive load based on different particle sizes has been proposed (Fig. 6). During compression testing, composites with larger particle size tended to experience a severe disturbance of opening matrix angle within the system, which will eventually result in bigger cracking diameter compared with composites with smaller particles.

Fig. 5. True stress/strain curves of sawdust/HDPE composites with (A) 500 µm, (B) 250 µm, (C) 125 µm, and (D) 63 µm particle under different loading rates
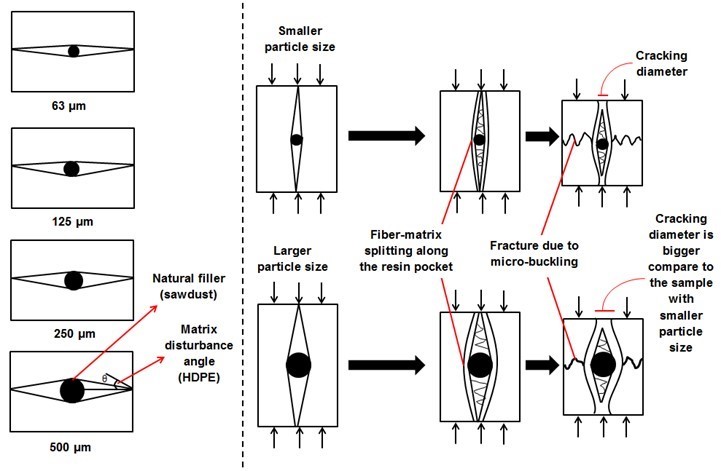
Fig. 6. The deduced failure mechanism under compressive load based on different particle sizes
Stiffness and Strength Properties
The stiffness of a material represents its ability to resist deformation and is characterized by the slope of the linear region of the stress-strain curve (Zabashta 1974). The strength is defined as the maximum stress that the material can sustain under uniaxial compression loading (Kalia et al. 2009). Both of these properties have been used as basic principles throughout the evaluation of material performance. Therefore, these properties were used to assess the performance of the sawdust/HDPE composites as a function of filler size (Figs. 7 and 8). The relationship between particle size and compression modulus was almost identical under both static and dynamic loadings (Fig. 7). Hence, the compression modulus increased steadily with decreasing particle size. This obvious difference in the result between neat HDPE and its composite was initiated by the addition of filler in the matrix, which made it more rigid (Supri and Lim 2009).
At strain rates of 0.001 s-1 and 1100 s-1, the compression modulus of sawdust/HDPE with a particle size of 63 µm increased by approximately a 78.9% and 24.3%, respectively, compared with neat HDPE. In contrast, sawdust/HDPE with a larger particle size (125 µm, 250 µm, and 500 µm) recorded a lower increment in terms of compression modulus compared with the control. In addition, based on one-way ANOVA analysis, at 0.001 s-1 and 1100 s-1 strain rate, the p-value is equal to 0.0001 and 0.0000, respectively, where the value is less than 0.05. These findings indicate a significant difference of compression modulus between those fillers (63 µm, 125 µm, 250 µm, and 500 µm). Theoretically, compression modulus elasticity increases with the addition of micro-particles to a polymer matrix, due to the fact that hard particles have much higher stiffness values than the matrix (Fu et al. 2008). This improvement is more significant when adding smaller particles, as smaller particles increase the stiffness within the composite system more than larger particles (Onuegbu and Igwe 2011).
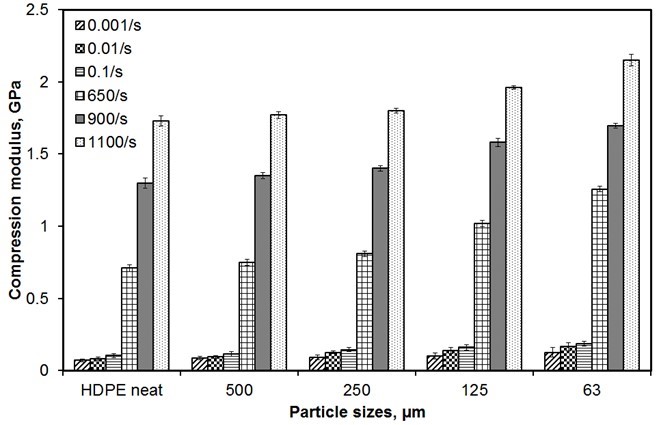
Fig. 7. The compression modulus of neat HDPE and sawdust/HDPE composites under various loading rates as a function of particle sizes
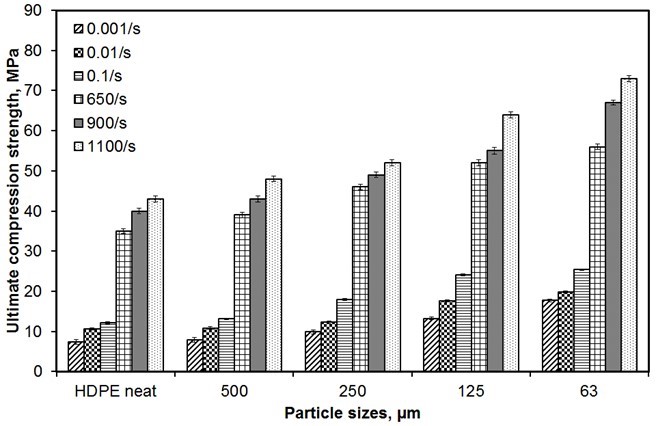
Fig. 8. The ultimate compression strength of HDPE and sawdust/HDPE composites under various loading rates as a function of particle size
Further analysis was carried out on the strength properties of sawdust/HDPE composite as a function of particle size (Fig. 8). The dependency between particle size and ultimate compression strength (UCS) was practically identical under both static and dynamic situations; UCS increased progressively with decreasing particle size. Based on one-way ANOVA analysis, the p-value under 0.001 s-1 and 1100 s-1 strain rate was 0.000. From the statistical point of view, a probability (p-value) less than 0.05 implies that there was a significant difference of the compared parameter between groups. In this case, it shows that there was a significant difference of ultimate compression strength between involved fillers (63 µm, 125 µm, 250 µm, and 500 µm), where the smallest particle recorded higher values. In regard to surface area, smaller particles have a higher total surface area than larger particles upon wide strain rate loading. It follows that the strength increased with increasing surface area of the filler particles through a more efficient stress transfer mechanism (Fu et al. 2008). This result also suggests that when the particle size is relatively large, reducing its size effectively improves the compression strength of the composites. This conclusion is valid for the micro-composites shown in the results above, but it does not apply to nanocomposites due to the effect that nanoparticle size has on strength (Mishra et al. 2005). Furthermore, the UCS values for all tested specimens in Fig. 8 also increased with increasing strain rate. Hypothetically, restriction of the polymer chain movement at high strain rate loading may also enhance the formation of additional Van der Waals interactions between structures. These additional interactions strengthen the polymer composite as the strain rate increases (Omar et al. 2011b).
Strain Rate Sensitivity and Thermal Activation Volume
In order to ease the comparison of strain rate sensitivity between specimens, it is often useful to obtain the results in terms of values. Thus, the strain rate sensitivities were calculated using an established parameter, which is shown in the following equation:
![]() (4)
(4)
where σ1 and σ2 are the flow stress at the fixed strain (0.025) under various strain rates, and and represent the strain rate investigated. At a strain of 0.025, the flow stresses of every specimen under various strain rates remained below the UCS point, giving useful knowledge in terms of stress/strain behavior. There is a definite relationship between strain rate sensitivity and thermal activation volume of the material (Hobeika et al. 2000), which can be expressed by the following equation (Omar et al. 2011a,b),
![]() (5)
(5)
where k is the Boltzmann constant and T is the absolute temperature. Thermal activation is defined as a dislocation-affected region in plastic deformation (Hobeika et al. 2000); in polymers, dislocation refers to the motion results in the rapid transfer of mass along the polymer chains (Zabashta 1974). The calculated strain rate sensitivities and thermal activation volumes of sawdust/HDPE composite specimens are shown in Table 1.
The sawdust particle size had a substantial influence on both the strain rate sensitivity and the thermal activation volume under both static and dynamic loadings. The data demonstrated that smaller particles progressively decreased the strain rate sensitivity of the HDPE/SD composites. Also, the percentage of rate sensitivity reduction between 63 µm and 125 µm was approximately 70% and 10%, under both static and dynamic loadings, respectively. Usually, during the selection of material for extreme applications, the data of strain rate sensitivity would be very useful, where material with less sensitivity properties were required (Omar et al. 2013).
Table 1. The Rate Sensitivities and Thermal Activation Volume of the Neat HDPE and the Sawdust/HDPE Measured Under Static and Dynamic Regions
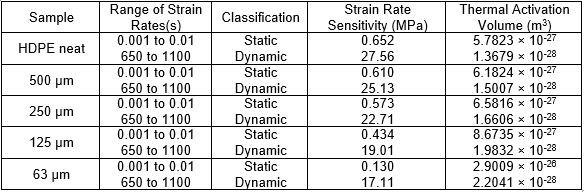
The strain rate sensitivity is frequently used to describe the variation in flow stress, and it corresponds to increasing strain rate, defined as σ/έ, where σ and έ are the flow stress and strain rate, respectively (Korla and Chokshi 2010). In this case, it appeared that the particle surface area influenced the flow stresses (σ: F/A) within the composite system when it was subjected to a force. Theoretically, during loading, composites containing smaller particles (larger surface area) would contribute to the lower flow stress distribution within the composite system, which would eventually decrease the strain rate sensitivity of the flow stresses. However, HDPE/SD composites with smaller particles showed increased thermal activation volume under both static and dynamic loadings. Therefore, the motion of polymer chains was less constrained with smaller particles, which resulted in high thermal activation volume.
Post Damage Analysis
Physical analysis
Figure 9 shows images of neat HDPE and HDPE/SD composites under a wide range of low strain rate loadings (0.001/s, 0.01/s, and 0.1/s). All HDPE/SD composites showed increasing deformation as the strain rate increased.
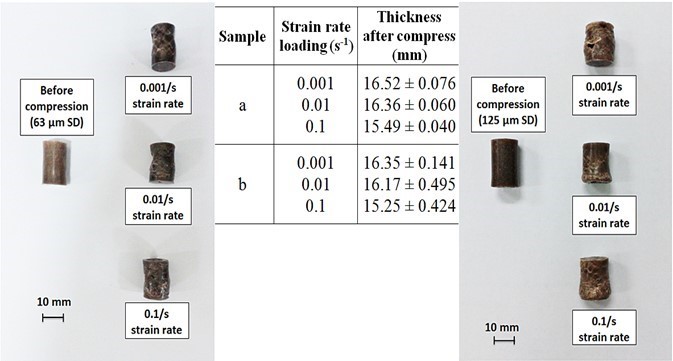
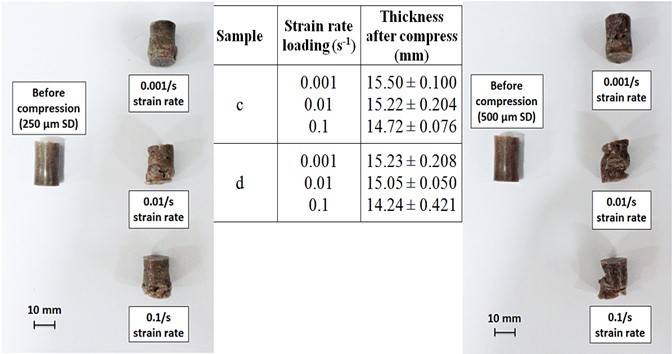
Fig. 9. Deformation of HDPE/SD composites with various particle sizes of (a) 63 µm SD, (b) 125 µm SD, (c) 250 µm SD, and (d) 500 µm SD under wide ranges of static loading
Additionally, composites with larger particles showed dramatic deformation, but the least amount of deformation was observed in composites with the smallest particle size. The samples also became shorter and tended to buckle at the bottom. Furthermore, specimens under dynamic loading also expressed the same trend of deformation, where the rate of deformation increased as the strain rate increased (Fig. 10).
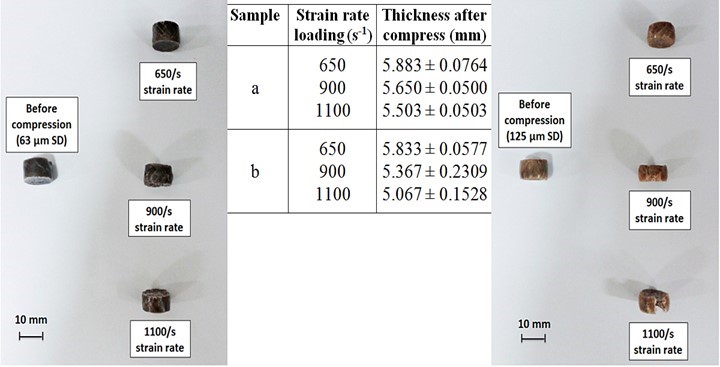
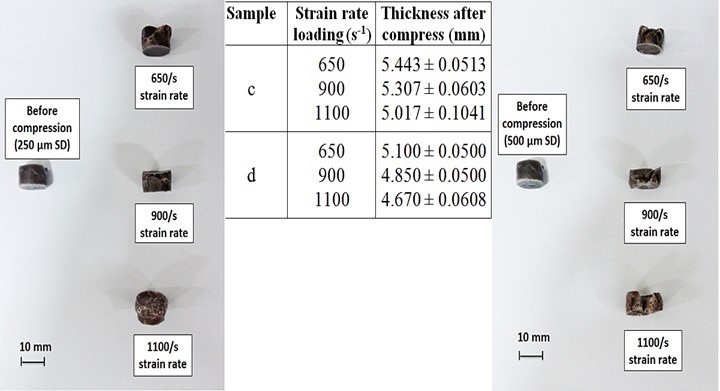
Fig. 10. Deformation of HDPE/SD composites with various particle sizes of (a) 63 µm SD, (b) 125 µm SD, (c) 250 µm SD, and (d) 500 µm SD under wide ranges of dynamic loading
The composite with a larger particle size (500 µm) revealed the most severe damages (cracking). These physical observations proved that the smaller particle size improved the sawdust filler properties and indirectly enhanced the performance of the composites. Interestingly, the photographs in Figs. 9 and 10 showed a good correlation with the stress/strain characteristic discussed in reference to Fig. 5. It was physically shown that the catastrophic fractures could only be seen under a dynamic loading and not under a static loading. All tested specimens were measured and summarized in Figs. 9 and 10.
Fractographic analysis
The fractographic features of the sawdust/HDPE composites under a high strain rate of compression loading were identified by the microscopic observation of failed composite fracture surfaces after high impact loading (Fig. 11). Figure 11 shows SEM micrographs of the dynamic compression fracture at a dynamic loading of 1100 s-1 in sawdust/HDPE composites with different sawdust particle sizes.

Fig. 11. The fracture surface of sawdust/HDPE composites with various particle sizes of (a) 500 µm, (b) 250 µm, (c) 125 µm, and (d) 63 µm under 1100 s-1 of strain rate
Three critical failure mechanisms were identified: translaminar fracture, intralaminar fracture, and interlaminar fracture. One of the first damages that occurs in composites is matrix cracking, which runs parallel to the fillers at a much lower stress (Kashtalyan and Soutis 2007). Matrix cracks develop in the filler direction, and multi-directional cracks form when the density of the matrix cracks increases with the increase in applied load (Zhang et al. 1999). When the matrix is sufficiently stiff and strong, alternative failure modes intervene, such as filler crushing. Filler crushing occurs when the uniaxial strain in the composite is equal to the intrinsic crushing strain (εfc) of the fillers (Fleck and Shu 1995). Subsequently, interlaminar delaminations develop and extend at the tip of the matrix cracks. The stress in the primary load-bearing layer is redistributed, leading to the ultimate failure of composite structures. These damages were severe under composites with larger particle sizes. This observation was in agreement with the explanation made in Figs. 7 and 8, where composites with the smallest particle size (63 µm) recorded higher compression properties than their counterparts with larger sizes.
CONCLUSIONS
Both static and dynamic mechanical tests were executed to determine the effect of particle sizes of sawdust/HDPE composites up to nearly 1100 s-1 of strain rates using the split Hopkinson pressure bar apparatus. From the overall results, the following conclusions were drawn:
- It was found that the stress/strain characteristics of the sawdust/HDPE composites were influenced by particle sizes, where for example the larger the particles in the composite, the greater would be the toughening effect.
- Apart from that, the strain rate sensitivity and thermal activation volume of all tested sawdust/HDPE composites were also calculated. Based on the calculated values, it was found that the reduction in sawdust particle size also significantly decreased the rate sensitivity of the sawdust/HDPE composites, whereas the thermal activation volume showed a contrary trend.
- Finally, for the post-damage analysis, it was found that all tested sawdust/HDPE composite specimens experienced severe catastrophic fractures under dynamic loading. Meanwhile, no fracture was observed in the case of static loading. Thus, it was physically verified that the catastrophic fractures can only be seen under a dynamic loading, rather than under static loading.
ACKNOWLEDGMENTS
The authors thank Universiti Malaysia Perlis (UniMAP) (Grant no.: 9003-00390, 9007-00067, 9017-00014, 9007-00130) for sponsoring and providing financial assistance for this research work.
REFERENCES CITED
ASTM E9-89. (1995). “Standard test methods of compression testing of metallic materials at room temperature,” ASTM International, West Conshohocken, PA, USA.
Ashori, A., and Nourbakhsh, A. (2009). “Reinforced polypropylene composites: Effects of chemical compositions and particle size,” Bioresource Technology, 101, 2515-2519. DOI: 10.1016/j.biortech.2009.11.022
Beer, F. P., Johnston Jr, E. R., and DeWolf, J. (2001). “Stress and strain–Axial loading,” in: Plant, J., (ed.), Mechanics of Materials, 3rd Ed., McGraw-Hill, New York, pp. 48-57.
Dubnikova, I., Berezina, S., and Antonov, A. (2004). “Effect of rigid particle size on the toughness of filled polypropylene,” Journal of Applied Polymer Science 94(5), 1917-1926. DOI: 10.1002/app.21017
Fleck, N. A., and Shu, J. Y. (1995). “Microbuckle initiation in fibre composites: A finite element study,” Journal of the Mechanics and Physics of Solids 43(12), 1887-1918. DOI: 10.1016/0022-5096(95)00057-P
Fu, S.-Y., Feng, X.-Q., Lauke, B., and Mai, Y.-W. (2008). “Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites,” Composites Part B: Engineering 39(6), 933-961. DOI: 10.1016/j.compositesb.2008.01.002
Guo, Y., and Li, Y. (2007). “Quasi-static/dynamic response of SiO2–epoxy nanocomposites,” Materials Science and Engineering: A, 458(1), 330-335. DOI: 10.1016/j.msea.2007.02.011
Hobeika, S., Men, Y., and Strobl, G. (2000). “Temperature and strain rate independence of critical strains in polyethylene and poly (ethylene-co-vinyl acetate),” Macromolecules 33(5), 1827-1833. DOI: 10.1021/ma9910484
Hossain, M. F., Shuvo, S. N., and Islam, M. A. (2014). “Effect of types of wood on the thermal conductivities of wood saw dust particle reinforced composites,” Procedia Engineering 90, 46-51. DOI: 10.1016/j.proeng.2014.11.812
Jaya, H., Omar, M. F., Md Akil, H., Ahmad, Z. A., and Zulkepli, N. N. (2016). “Effect of alkaline treatment on sawdust reinforced high density polyethylene composite under wide strain rate,” Materials Science Forum 840, 103-107. DOI: 10.4028/www.scientific.net/MSF.840.103
Kalia, S., Kaith, B., and Kaur, I. (2009). “Pretreatments of natural fibers and their application as reinforcing material in polymer composites—a review,” Polymer Engineering & Science 49(7), 1253-1272. DOI: 10.1002/pen.21328
Kashtalyan, M., and Soutis, C. (2007). “Stiffness and fracture analysis of laminated composites with off-axis ply matrix cracking,” Composites Part A: Applied Science and Manufacturing 38(4), 1262-1269. DOI: 10.1016/j.compositesa.2006.07.001
Kitey, R., and Tippur, H. (2005). “Role of particle size and filler–matrix adhesion on dynamic fracture of glass-filled epoxy. I. Macromeasurements,” Acta Materialia, 53(4), 1153-1165. DOI: 10.1016/j.actamat.2004.11.011
Korla, R., and Chokshi, A. H. (2010). “Strain-rate sensitivity and microstructural evolution in a Mg–Al–Zn alloy,” Scripta Materialia 63(9), 913-916. DOI: 10.1016/j.scriptamat.2010.06.047
Lauke, B. (2009). “Effect of particle size distribution on fracture toughness of polymers,” Proceedings of 11th Pan-American Congress of Applied Mechanics.
Lu, H., Ip, E., Scott, J., Foster, P., Vickers, M., and Baxter, L. L. (2010). “Effects of particle shape and size on devolatilization of biomass particle,” Fuel 89(5), 1156-1168. DOI: 10.1016/j.fuel.2008.10.023
Mishra, S., Sonawane, S., and Singh, R. (2005). “Studies on characterization of nano CaCO3 prepared by the in situ deposition technique and its application in PP‐nano CaCO3 composites,” Journal of Polymer Science Part B: Polymer Physics 43(1), 107-113. DOI: 10.1002/polb.20296
Moschakis, T., Murray, B. S., and Dickinson, E. (2005). “Microstructural evolution of viscoelastic emulsions stabilised by sodium caseinate and xanthan gum,” Journal of Colloid and Interface Science 284(2), 714-728. DOI: 10.1016/j.jcis.2004.10.036
Nakai, K., and Yokoyama, T. (2008). “Strain rate dependence of compressive stress-strain loops of several polymers,” Journal of Solid Mechanics and Materials Engineering 2(4), 557-566. DOI: 10.1299/jmmp.2.557
Omar, M. F., Akil, H. M., and Ahmad, Z. A. (2011a). “Mechanical properties of nanosilica/polypropylene composites under dynamic compression loading,” Polymer Composites 32(4), 565-575. DOI: 10.1002/pc.21079
Omar, M. F., Akil, H. M., and Ahmad, Z. A. (2011b). “Static and dynamic compressive properties of mica/polypropylene composites,” Materials Science and Engineering: A, 528(3), 1567-1576. DOI:10.1016/j.msea.2010.10.071
Omar, M. F., Akil, H. M., and Ahmad, Z. A. (2013). “Particle size – Dependent on the static and dynamic compression properties of polypropylene/silica composites,” Materials & Design 45, 539-547. DOI:10.1016/j.matdes.2012.09.026
Omar, M. F., Akil, H. M., Ahmad, Z. A., and Mahmud, S. (2012). “The effect of loading rates and particle geometry on compressive properties of polypropylene/zinc oxide nanocomposites: experimental and numerical prediction,” Polymer Composites 33(1), 99-108. DOI: 10.1002/pc.21253
Onuegbu, G. C., and Igwe, I. O. (2011). “The effects of filler contents and particle sizes on the mechanical and end-use properties of snail shell powder filled polypropylene,” Materials Sciences and Applications 2(07), 810. DOI: 10.4236/msa.2011.27110
Rahman, M. R., Islam, M. N., and Huque, M. M. (2010). “Influence of fiber treatment on the mechanical and morphological properties of sawdust reinforced polypropylene composites,” Journal of Polymers and the Environment 18(3), 443-450. DOI: 10.1007/s10924-010-0230-z
Supri, A., and Lim, B. (2009). “Effect of treated and untreated filler loading on the mechanical, morphological, and water absorption properties of water hyacinth fibers-low density polyethylene composites,” Journal of Physical Science 20(2), 85-96.
Zabashta, Y. F. (1974). “On the dislocation mechanism of polymer deformation: Defects of spiral molecules.” Polymer Mechanics 10(4), 493-496. DOI: 10.1007/BF00855438
Zhang, J., Fan, J., and Herrmann, K. (1999). “Delaminations induced by constrained transverse cracking in symmetric composite laminates,” International Journal of Solids and Structures 36(6), 813-846. DOI: 10.1016/S0020-7683(97)00325-9
Zhang, S., Cao, X., Ma, Y., Ke, Y., Zhang, J., and Wang, F. (2011). “The effects of particle size and content on the thermal conductivity and mechanical properties of Al2O3/high density polyethylene (HDPE) composites,” Express Polymer Letters 5(7), 581-590. DOI: 10.3144/expresspolymlett.2011.57
Article submitted: February 26, 2016; Peer review completed: May 9, 2016; Revised version received and accepted: May 30, 2016; Published: June 20, 2016.
DOI: 10.15376/biores.11.3.6489-6504
