Effect of water molecules at different temperatures on properties of cellulose based on molecular dynamics simulation

Wang, W., Ma, W., Wu, M., and Sun, L. (2022). "Effect of water molecules at different temperatures on properties of cellulose based on molecular dynamics simulation," BioResources, 17(1), 269-280.

Abstract

Six hybrid models of cellulose amorphous region and water molecules were established by using a molecular dynamics software to simulate changes of cellulose and water molecules during bamboo hydrothermal treatment. The results indicated that in the range of hydrothermal treatment temperature of bamboo from 150 to 240 °C, the diffusion coefficient of water molecules increased with the increase of temperature, conducive to the processing efficiency of hydrothermal treatment. The mean square displacement (MSD) of the bamboo cellulose chain increased with the increase of temperature, not conducive to the thermal stability of cellulose. The energy change of the system predicts that a higher hydrothermal treatment temperature will result in faster material aging degradation. The comprehensive analysis of mechanical parameters showed that when the hydrothermal treatment temperature did not exceed 180 °C, bamboo cellulose had better plasticity and toughness.

Download PDF

Full Article

Effect of Water Molecules at Different Temperatures on Properties of Cellulose Based on Molecular Dynamics Simulation

Wei Wang,* Wei Ma, Mingshuai Wu, and Liyue Sun

DOI: 10.15376/biores.17.1.269-280

Keywords: Bamboo heat treatment; Molecular dynamics; Diffusion coefficient; Energy change; Mechanical properties

Contact information: College of Engineering and Technology, Northeast Forestry University, Harbin 150040, China; *Corresponding author: vickywong@nefu.edu.cn; cestlavie28@163.com

INTRODUCTION

Bamboo is a natural material with a short production cycle and high mechanical strength, which has great development potential (Sharma et al. 2015). Bamboo is widely used in decoration, architecture, furniture, and many other fields (Asif 2009; Febrianto et al. 2012; Qi et al. 2014; Sun et al. 2020)(!!! INVALID CITATION !!! {Asif, 2009 #14;Febrianto, 2012 #15;Qi, 2014 #16;Sun, 2020 #17}){Asif, 2009 #14;Febrianto, 2012 #15;Qi, 2014 #16;Sun, 2020 #17}. However, bamboo also has many disadvantages, including its low natural durability and the fact that its size tends to change if the environment changes (Colla et al. 2011){Colla, 2011 #18}. Because bamboo is made up of cellulose, hemicellulose, sugars, proteins, and starch, it is prone to mildew, cracking, and moth-eating problems (Liese 1980; Liese 2003). Therefore, the modification of bamboo has a strong practical significance.

Heat treatment can be used to improve the performance of bamboo products (Tao et al. 2015). Bamboo heat treatment is similar to wood heat treatment. It uses air, inert gas, or steam as a heat transfer agent for physical modification treatment at high temperatures between 150 to 240 °C. Heat treatment improves the physical properties, dimensional stability, and hygroscopicity of bamboo because of the change of surface and internal structure and composition of bamboo (Cao et al. 2012; Wang et al. 2018). Appropriate treatment temperature reduces the hygroscopicity and water absorption of bamboo and improves the dimensional stability and durability of bamboo. The high temperature leads to surface hardening and reduces its mechanical strength, which reduces the comprehensive strength of bamboo and affects its application in bamboo products and the bamboo industry (Yang et al. 2016; Azadeh and Ghavami 2018). Different treatment temperatures have a significant effect on the properties of bamboo after hydrothermal treatment.

Many studies have revealed the effect of temperature on the properties of bamboo. Bui et al. (2017) found that bamboo has the best durability and mechanical properties when the temperature is 180 °C and the treatment time is 1 to 2 h. Wang et al. (2020c) reported that high temperature saturated steam treatment reduces the equilibrium moisture content of bamboo and improves the dimensional stability and durability of bamboo stalks; the 180 °C treatment for 10 min is a favorable treatment condition. Wang et al. (2020a) found that the compressive strength, bending strength, and bending elastic modulus of bamboo are increased, while the shear strength is decreased when the temperature is 180 °C.

Hydrothermal treatment can improve the properties of bamboo. Studies have shown that the heat treatment of bamboo in water vapor at suitable temperature can improve the dimensional stability and durability of bamboo. But temperature that is too high will reduce its mechanical strength. Therefore, it is important to find the right hydrothermal treatment temperature.

With the development of heat treatment and molecular dynamics technology, the research on cellulose from the microscopic level of bamboo has gradually become a hotspot of research. Khazraji and Robert (2013) found that the cellulose polymer has strong reactivity with water molecules, and water molecules easily form a hydrogen bonds with the cellulose chain. Huang et al. (2019) revealed that ammonia molecules increase the end distance of cellulose Iβ and thus enhance its compliance. Wang et al. (2020b) found that the mass fraction of water molecules has a greater impact on bamboo heat treatment through molecular dynamics simulation, and cellulose has the best mechanical properties when the mass fraction of water was 3% for heat treatment simulation.

While it is common to study the interaction between cellulose and small molecules from the microscopic point of view, there have been few reports on the effect of temperature on the related properties of bamboo hydrothermal treatment. The goal of this work was to study the effect of water molecules on the mechanical properties of cellulose in the process of bamboo hydrothermal treatment at different temperatures from a microscopic perspective. An attempt is made in this work to find a suitable range of temperature during hydrothermal treatment of bamboo, to provide relevant theoretical support for bamboo hydrothermal treatment.

EXPERIMENTAL

Method

Modeling

Cellulose, the main component of bamboo, is a polymeric compound formed by the polymerization of D-glucopyranose. It consists of crystalline and amorphous regions. The cellulose molecules in the crystalline zones are arranged in a compact and orderly manner, and their mechanical properties are difficult to be broken at high temperatures. However, the amorphous region of cellulose has an irregular structure and good flexibility, which can make the cellulose material show a soft side, and its mechanical properties are easily affected by temperature (Khazraji and Robert 2013). Therefore, the amorphous region was selected to study the effect of temperature on bamboo hydrothermal treatment.

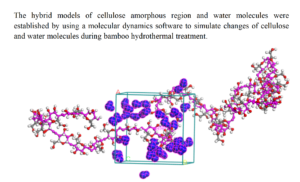
The amorphous region of the bamboo cellulose molecular chain was modeled using Materials Studio 8.0 software (BIOVIA, v.8.0, San Diego, CA, USA). The degree of polymerization (DP) has no remarkable effect on the simulation results of the physical properties of the material (Mazeau and Heux 2008). In this paper, a cellulose chain was created with a DP of 20 (Wang et al. 2018). The construction of the amorphous region polymer adopts the method proposed by Theodorou and Suter (1985) and uses the Amorphous Cell Tools (AC) module for modeling. The model target density was set to 1.5 g/cm³ (Onyon 1972). In the model, 30 water molecules and a cellulose chain with a DP of 20 were added. The size of the simulated unit cell was 20.2 × 20.2 × 20.2 (A³). The established model is shown in Fig. 1.

Fig. 1. Cellulose amorphous region-water model. The red chain is a bamboo cellulose molecular chain, and the blue spheres are water molecules.

Dynamic simulation

The model shown in Fig. 1 was optimized for structure and energy minimization. The Forcite Calculation module was used for structural optimization, and the smart algorithm was chosen to run 5000 steps. The dynamic relaxation of the model was carried out at 25 °C in the canonical ensemble (NVT) for 1000 ps to minimize the energy of the system. The time step was 1 ps. One frame was output every 5000 steps, and the Nose method was selected as the temperature control method. The temperature of bamboo hydrothermal treatment starts from 90 °C and increases by 30 °C each time to 240 °C. This temperature range includes the set temperature required for the bamboo hydrothermal treatment process.

The dynamic simulation was of the model carried out in the isothermal isobaric ensemble (NPT) with a time of 1000 ps. The Andersen method was selected as the temperature control method (Andrea et al. 1983); the Berendsen method was selected as the pressure control method (Berendsen et al. 1984). The Van der Waals force was computed by atom-based calculations (Andersen 1980); the electronic effect was computed by the Ewald method (Ewald 1921). All simulations were performed under the PCFF force field, which originated from the CFF91 force field. It is suitable for calculating organic compounds, especially natural polymer materials.

RESULTS AND DISCUSSION

The Energy

In molecular dynamics simulation, energy was used as the basis for system equilibrium. Figure 2 shows the dynamic energy diagram of the bamboo cellulose-water molecule model. The total energy values of the last 200 ps fluctuated slightly above and below its average value, which showed that the system tends to equilibrium.

Fig. 2. The dynamics energies of model

In Fig. 2, Potential represents total potential energy, Kinetic represents kinetic energy, Non-bond represents non-bond energy term, and Total represents total energy. The non-bond energy term includes electrostatic interaction and van der Waals interaction. In this paper, the PCFF force field is selected, and its total potential energy expression is more complicated (Sun 1995; Maple et al. 2013). It can be simply expressed as Eq. 1,

(1)

where E_nonbond is the non-bond energy term, and (E_cross + E_internal) is the sum of the potential energy of the water molecule and the cellulose molecule, called the bond energy term. The total potential energy of the system is equal to the sum of non-bond energy term and bond energy term. In the simulation process, as the temperature increases, when the total potential energy exceeds the non-bonded energy term, the bond energy term changes from a negative value to a positive value. That means covalent bonds are becoming more unstable. As the heat energy increases, the bond energy term increases and the covalent bond becomes unstable. Some active bonds in the bamboo material are unstable or even broken, which leads to bamboo cellulose aging and degradation.

As shown in Fig. 3, the mean value of the non-bond energy term and the mean value of the total potential energy showed a linear increasing trend with increased temperature; when the temperature was greater than 120 °C, the mean value of the total potential energy gradually became larger than the mean value of the non-bond energy term. The mean value of the bond energy term changes from negative to positive. The bond energy is the difference between the total potential energy and the non-bond energy, as shown in Table 1.

Fig. 3. The average energies of the model at different temperatures

Table 1. The Average Bond Energy of the Model at Different Temperature

The bond energy term increased continuously with the increasing temperature. According to these data, temperature damages bamboo fiber. Therefore, to meet the basic temperature requirements of hydrothermal treatment, the temperature should be lowered as much as possible to reduce the influence of temperature on bamboo.

Diffusion Coefficient of Water Molecules

The diffusion coefficient is an important parameter that reflects the ability of small molecules to diffuse in a substance. The size of the diffusion coefficient can be calculated by the mean square displacement (MSD). The MSD refers to the mean square sum of the vector increment of the water molecule position after the dynamic simulation, as represented by Eq. 2,

where N_w is the number of water molecules in the system. The Einstein relationship can be used to solve the diffusion coefficient by the slope of the mean square displacement when t is large enough (Yang et al. 2013), as shown in Eq. 4,

where K represents the slope of the mean square displacement (MSD) curve. Based on the analysis of the model, the MSD at different temperatures was obtained (Fig. 4).

Fig. 4. Mean squared displacement curves of water at different temperatures

As shown in Fig. 4, the MSD of water molecules increased linearly with time in the simulation time of 0 to 900 ps, and a there was a large deviation from 900 to 1000 s. This deviation can be regarded as a statistical error calculation. The first 900 ps was fit according to the principle of the least square method to find the size of the diffusion coefficient, as shown in Table 2. The diffusion coefficient of the water molecule in the cellulose model increased with rising temperature; at higher temperatures, more energy is absorbed by water molecules. With the increase of its energy, the thermal motion of water molecules becomes more violent, which makes it easier to penetrate the bamboo cellulose chain, thereby improving the processing efficiency of bamboo hydrothermal treatment.

Table 2. Diffusion Coefficient D of Water at Different Temperatures

The MSD of the Bamboo Cellulose Chain

There are five crystalline variants of cellulose in the solid-state, namely cellulose I, II, III, IV, and X. Cellulose I belongs to natural cellulose. It has two different crystalline phases, Iα and Iβ. The former mainly exists in bacterial fibers and belongs to the triclinic unit cell model, while the latter mainly exists in animal fibers and higher angiosperms. It belongs to the monoclinic unit cell model (O’Sullivan 1997). Bamboo cellulose, wood cellulose, and cotton and linen fibers are all-natural cellulose and are derived from higher angiosperms, so their main component cellulose has similar structure and properties. The MSD of the bamboo cellulose chain can indicate the movement of the cellulose molecular chain. The violent movement of the bamboo cellulose chain determines its stability. More movement indicates decreased stability. Therefore, the stability of the overall bamboo structure is reduced. As shown in Fig. 5, the MSD of cellulose molecules increased linearly with time in the simulation time of 0 to 900 ps. Within the scope of 900-1000 ps curve appeared different degree of deviation, because the calculation includes the statistical error. In the temperature range of 90 to 150 °C, the MSD of the bamboo cellulose molecular chain did not change significantly. In the temperature range of 180 to 240 °C, the MSD of the bamboo cellulose molecular chain increased with increasing temperature. Further analysis showed that when the hydrothermal treatment temperature was within the range 160 to 240 °C, the stability of bamboo cellulose decreased with increasing temperature.

Fig. 5. Mean squared displacement curves of bamboo cellulose at different temperatures

Mechanical Properties

The dynamic mechanical parameters of the bamboo cellulose amorphous zone model at different temperatures characterize the effect of temperature on the changes in the mechanical properties of bamboo. Cauchy pressure (C12-C44) is usually used to measure the ductility of a system, which is the ability of a material to deform without cracking. The higher the value is, the better the ductility of the system is. In general, a material with good ductility will have a positive value (C12-C44); otherwise it will have a negative value. Young’s modulus (E) is the longitudinal elastic modulus, which is used to characterize the ability of a material to resist deformation. A larger value indicates the ability of the material to resist deformation. Shear modulus (G) characterizes the ability of a material to resist shear strain, where a larger value represents stronger rigidity and less ductility. Poisson’s ratio (γ) is the absolute value of the ratio of the material’s transverse variable to the longitudinal variable when the material is subjected to external stress. A greater value results in stronger plasticity. The larger ratio of bulk modulus to shear modulus (K/G) indicates greater toughness in the material. The parameters of mechanical properties at different temperatures were obtained by the Forcite module in MS, and the results are shown in Table 3.

Table 3. Elastic Stiffness Constant of Cellulose Models at Different Temperature

When the treatment temperature is 90 ℃, the Cauchy pressure is negative, indicating that the ductility of the system is poor. However, with the increase of temperature, the value of Cauchy pressure increased significantly and showed an increasing trend after 150 ℃, indicating that the ductility of the system was good and had a better and better trend. The authors believe that this is due to the low temperature at 90 ℃ and the weak interaction between water molecules and cellulose, which results in poor ductility. With the increase of temperature, the interaction between water molecules and cellulose becomes more intense, which increases its ductility. An extreme value appears at 120 ℃, which may be because the non-bond energy is the closest to the total potential energy and the bond energy is the smallest, leading to the system in an equilibrium state.

The parameters λ and μ are called Lame constants. They can be calculated by the Forcite module. Lame constants can be used to calculate Young’s modulus (E), shear modulus (G), Poisson’s ratio (γ), bulk modulus (K), as follows,

(5)

(6)

(7)

(8)

As shown in Table 4, with increasing temperature, the value of Young’s variable with the boundary of 180 °C decreased first and then increased. Thus, the flexibility of bamboo material increased first and then decreased. Similarly, the value of shear modulus was smaller at 180 °C; with increasing temperature, the ductility at 180 °C decreased first and then increased. The values of Poisson’s ratio and K/G were higher than other setting temperatures at 180 °C, but if the temperature continues to rise, the Poisson’s ratio and K/G values gradually decreased. When the treatment temperature is below 180 °C, due to the increase of temperature, the interaction between water molecules and cellulose becomes more and more sufficient, leading to the mechanical properties of bamboo gradually becoming better. With the increase of temperature, the intermolecular bond energy gradually increases. When the temperature exceeds 180 ℃, some active bonds in the bamboo material are unstable or even broken due to the large repulsive force between the atoms within the molecule, which leads to the deterioration of the mechanical properties of the bamboo cellulose. At 120 ℃, the mechanical properties of cellulose are also better, which may be attributed to the lowest bond energy term in the system and the equilibrium state.

The simulation results are consistent with good plasticity when the heating temperature does not exceed 180 °C. Overall, these results indicate that if bamboo heat treatment is to pursue better plasticity, toughness, and ductility in the process of selecting water vapor as the heat transfer medium, the temperature setting of bamboo hydrothermal treatment should not exceed 180 °C. It is also consistent with the conclusion that hydrothermal treatment at appropriate temperature can improve the bending elastic modulus of bamboo, and too high temperature will degrade its properties, which Yun et al. (2016) studied.

Table 4. Mechanical Parameter of the Model at Different Temperatures

CONCLUSIONS

When the temperature of the simulated system is greater than 120 °C, the total potential energy of the system begins to exceed the non-bond energy term, and the bond energy term gradually increases. As a result, the covalent bonds become unstable and the bamboo fiber begins to age and degrade.
The diffusion coefficient of water molecules gradually increases with the increase of the hydrothermal treatment temperature. As the temperature rises, water molecules absorb energy to increase their energy, leading to accelerated thermal movement of water molecules, which is more conducive to improving the diffusion coefficient and water molecules entering the bamboo cellulose chain, thus improving the heat treatment processing efficiency of bamboo.
The mean square displacement (MSD) of the bamboo cellulose chain is easily affected when the temperature is greater than 150 °C. If the temperature is increased in the range of hydrothermal treatment temperature, then the thermal stability of the bamboo cellulose chain will decrease, which will affect the stability of bamboo cellulose.
The Cauchy pressure of bamboo cellulose changed from a negative value to a positive value with the increase of temperature, indicating that heat treatment was beneficial to the improvement of bamboo cellulose ductility. Simultaneously, the values of Young’s variable and shear variable first decrease and then increase with the temperature increasing. Both have the minimum values at 180 °C and gradually increase when the temperature exceeds 180 °C. The values of Poisson’s ratio and K/G first increase and then decrease, and have a maximum value at 180 °C, and gradually decrease when above 180 °C. These results suggest that if the goal for the heat-treated bamboo is to achieve better plasticity, toughness, and ductility, then the heat treatment temperature should not exceed 180 °C.

ACKNOWLEDGMENTS

The authors are grateful for the support by The Fundamental Research Funds for the Central Universities (41419020).

REFERENCES CITED

Andersen, H. C. (1980). “Molecular dynamics simulations at constant pressure and/or temperature,” Journal of Chemical Physics 72(4), 2384-2393. DOI: 10.1063/1.439486

Andrea, T. A., Swope, W. C., and Andersen, H. C. (1983). “The role of long ranged forces in determining the structure and properties of liquid water,” Chemical Physics 79, 4576-4584. DOI: 10.1063/1.446373

Asif, M. (2009). “2–Sustainability of timber, wood and bamboo in construction,” Sustainability of Construction Materials 6(5), 31-54. DOI: 10.1533/9781845695842.31

Azadeh, A., and Ghavami, K. (2018). “The influence of heat on shrinkage and water absorption of Dendrocalamus giganteus bamboo as a functionally graded material,” Construction and Building Materials 186, 145-154. DOI: 10.1016/j.conbuildmat.2018.07.011

Berendsen, H. J. C. P., Postma, J., Gunsteren, W., Dinola, A. D., and Haak, J. R. (1984). “Molecular-dynamics with coupling to an external bath,” The Journal of Chemical Physics 81, 3684. DOI: 10.1063/1.448118

Brown, W. R., Jenkins, R. B., and Park, G. S. (2010). “The sorption and diffusion of small molecules in amorphous and crystalline polybutadienes,” Journal of Polymer ence Polymer Symposia 41(1), 45-67. DOI: 10.1002/polc.5070410107

Bui, Q.-B., Grillet, A. C., and Tran, H.-D. (2017). “A bamboo treatment procedure: Effects on the durability and mechanical performance,” Sustainability 9(9), 1444. DOI: 10.3390/su9091444

Cao, Y., Lu, J., , Huang, R., and Jiang, J. (2012). “Increased dimensional stability of Chinese fir through steam-heat treatment,” European Journal of Wood & Wood Products 70(4), 441-444. DOI: 10.1007/s00107-011-0570-y

Colla, W. A., Beraldo, A. L., and Brito, J. O. (2011). “Effects of thermal treatment on the physicochemical characteristics of giant bamboo,” Cerne 17(3), 361-367. DOI:
10.1590/S0104-77602011000300010

Einstein, A. (1905). “Zur Electrodynamik bewegter Korper,” Annalen der Physik 17.

Ewald, P. P. (1921). “Evaluation of optical and electrostatic lattice potentials,” Annals of Physics 64, 253-287.

Febrianto, F., Sahroni, Hidayat, W., Bakar, E. S., Kwon, G.-J., Kwon, J.-H., Hong, S.-I., and Kim, N.-H. (2012). “Properties of oriented strand board made from Betung bamboo (Dendrocalamus asper (Schultes.f) Backer ex Heyne),” Wood Science and Technology 46(1-3), 53-62. DOI: 10.1007/s00226-010-0385-8

Huang, S., Wu, X., and Li, P. (2019). “Diffusion behaviors of liquid ammonia in the cellulose based on molecular dynamics simulation,” International Journal of Clothing Science and Technology 31(5), 705-714. DOI: 10.1108/IJCST-12-2018-0163

Khazraji, A. C., and Robert, S. (2013). “Interaction effects betweeKhazraji, A. C., and Robert, S. (2013). “Interaction effects between cellulose and water in nanocrystalline and amorphous regions: A novel approach using molecular modeling,” Journal of Nanomaterials 2013, article ID 409676. DOI: 10.1155/2013/409676

Liese, W. (1980). “Preservation of bamboos,” Bamboo Research in Asia (https://xueshu.baidu.com/usercenter/paper/show?paperid=d90435335bb56b5818fd773bba652543&site=xueshu_se)

Liese, W. (2003). Centre for Indian Bamboo Resource and Technology, New Delhi, Kumar, S., Ny, A. B. S. A., & Delhi, B. R. N. (2003). Bamboo preservation compendium (https://xueshu.baidu.com/usercenter/paper/show?paperid=892d11699606cdfa1351a3ac3cccbe0a&site=xueshu_se)

Maple, J. R., Hwang, M. J., Stockfisch, T. P., and Hagler, A. T. (2013). “Derivation of class II force fields. III. Characterization of a quantum force field for alkanes,” Israel Journal of Chemistry 34(2), 195-231. DOI: 10.1002/ijch.199400025

Mazeau, K., and Heux, L. (2008). “Molecular dynamics simulations of bulk native crystalline and amorphous structures of cellulose,” Journal of Physical Chemistry B 107(10), 2394-2403. DOI: 10.1021/jp0219395

O’Sullivan, A. C. (1997). “Cellulose: The structure slowly unravels,” Cellulose 4(3), 173-207. DOI: 10.1023/A:1018431705579

Onyon, P. F. (1972). “Polymer Handbook,” Nature, 238(5358), 56-56. DOI: 10.1038/238056a0

Qi, J. Q., Xie, J. L., Huang, X. Y., Yu, W. J., and Chen, S. M. (2014). “Influence of characteristic inhomogeneity of bamboo culm on mechanical properties of bamboo plywood: Effect of culm height,” Journal of Wood Science 60(6), 396-402. DOI: 10.1007/s10086-014-1429-8

Sharma, B., Gatoo, A., Bock, M., and Ramage, M. (2015). “Engineered bamboo for structural applications,” Construction and Building Materials 81, 66-73. DOI: 10.1016/j.conbuildmat.2015.01.077

Sun, H. (1995). “Ab initio calculations and force field development for computer simulation of polysilanes,” Macromolecules 28(3), 701-712. DOI: 10.1021/ma00107a006

Sun, X., He, M., and Li, Z. (2020). “Novel engineered wood and bamboo composites for structural applications: State-of-art of manufacturing technology and mechanical performance evaluation,” Construction and Building Materials 249, 118751. DOI: 10.1016/j.conbuildmat.2020.118751

Tao, Li, Da-li, Cheng, Magnus, E., P., Wålinder, and Ding-guo, Zhou. (2015). “Wettability of oil heat-treated bamboo and bonding strength of laminated bamboo board,” Industrial Crops & Products. DOI: 10.1016/j.indcrop.2015.02.008

Theodorou, D. N., and Suter, U. W. (1985). “Detailed molecular structure of a vinyl polymer glass,” Macromolecules 18(7), 1467-1478. DOI: 10.1021/ma00149a018

Wang, Q., Wu, X., Yuan, C., Lou, Z., and Li, Y. (2020a). “Effect of saturated steam heat treatment on physical and chemical properties of bamboo,” Molecules 25(8). DOI: 10.3390/molecules25081999

Wang, W., Sun, L., Wu, M., Li, X., and Song, W. (2020b). “Molecular dynamics simulation of bamboo heat treatment with cellulose based on molecular different weight fractions of water,” BioResources 15(3), 6766-6780. DOI: 10.15376/biores.15.3.6766-6780

Wang, X., Cheng, D., Huang, X., Song, L., and Xu, B. (2020c). “Effect of high-temperature saturated steam treatment on the physical, chemical, and mechanical properties of moso bamboo,” Journal of Wood Science 66(1). DOI: 10.1186/s10086-020-01899-8

Wang, W., Wang, Y., and Li, X. (2018). “Molecular dynamics study on mechanical properties of cellulose with air/nitrogen diffusion behavior,” BioResources 13(4), 7900-7910. DOI: 10.15376/biores.13.4.7900-7910

Yang, L., Qi, C., Wu, G., Liao, R., Wang, Q., Gong, C., and Gao, J. (2013). “Molecular dynamics simulation of diffusion behaviour of gas molecules within oil–paper insulation system,” Molecular Simulation 39(12), 988-999. DOI: 10.1080/08927022.2013.788180

Yang, T. H., Lee, C. H., Lee, C. J., and Cheng, Y. W. (2016). “Effects of different thermal modification media on physical and mechanical properties of moso bamboo,” Construction & Building Materials 119, 251-259. DOI: 10.1016/j.conbuildmat.2016.04.156

Yun, H., Li, K.-F., Tu, D.-Y., and Hu, C.-S. (2016). “Effect of heat treatment on bamboo fiber morphology crystallinity and mechanical properties,” Wood Research 61(2), 227-233.

Article submitted: May 8, 2021; Peer review completed: July 17, 2021; Revised version received: August 2, 2021; Second revised version received: August 26, 2021; Accepted: November 13, 2021; Published: November 17, 2021.

DOI: 10.15376/biores.17.1.269-280