Estimating design values for two-pin moment resisting dowel joints with lower tolerance limit approach

Uysal, M., and Haviarova, E. (2018). "Estimating design values for two-pin moment resisting dowel joints with lower tolerance limit approach," BioRes. 13(3), 5241-5253.

Abstract

The lower tolerance limits (LTLs) for two-pin moment-resisting dowel joints, constructed of red oak and white oak, were estimated. Dowel joints are widely used in furniture manufacturing, especially for tables and chairs. Despite numerous studies to determine the strength capacities of dowel joints, their design values have not been established. For this purpose, T-shaped edgewise dowel joints were constructed to determine their ultimate failure load capacity levels. In tolerance analysis, the k-tolerance factor changes depending on sample sizes and confidence/proportion levels. Therefore, sample sizes were determined using a modified Faulkenberry-Week method for a univariate normally distributed data set created for a pilot study, which had 30 specimens. At least 215 specimens were required to make tolerance analyses at the 99/99 confidence/proportion level. Accordingly, 220 specimens were constructed. The LTL values were obtained at the 75/75, 90/75, 75/90, 90/90, 95/90, 90/95, 95/95, 99/95, 95/99, and 99/99 confidence/proportion levels to estimate reasonable design values. The results of the study indicated that the LTL method provides a sound design value estimate for dowel joints used in furniture frames.

Download PDF

Full Article

Estimating Design Values for Two-Pin Moment Resisting Dowel Joints with Lower Tolerance Limit Approach

Mesut Uysal and Eva Haviarova *

Keywords: Lower tolerance limits; Dowel joints; Joint design; Static load test

Contact Information: Department of Forestry and Natural Resources, Purdue University, 175 Marsteller Street, West Lafayette, IN 47907 USA; *Corresponding author: ehaviar@purdue.edu

INTRODUCTION

The mechanical properties of wood member and joint strength play a vital role in determining the strength of the furniture frames (Derikvand and Ebrahimi 2015). To produce durable furniture that is able to withstand usage loads, it is necessary to have rational estimates of the joint capacity used in its construction. Joints are the weakest part of the furniture structure and significantly influence its overall reliability. Accordingly, failures are typically due to loose or failed joints rather than fractured legs or rails (Eckelman et al. 2003). Thus, when designing furniture, it is essential to have reliable estimates of the load carrying capacities (and the variability of capacity) of the joints used in construction (Eckelman 1974).

Dowel joints are widely used in chairs and tables because of their favorable cost and production characteristics, and numerous studies have been conducted to determine their load capacity levels (Zhang and Eckelman 1993; Eckelman et al. 2002; Eckelman 2003; Tas 2010; Yerlikaya and Aktas 2013; Yerlikaya 2014). However, reasonable design values for dowel joints used in the furniture frames have not been established.

In engineering design, it is vital to manage data variability due to material properties. Identical samples may not provide similar test results due to inherent variation caused by inconsistency in the creation, location, and propagation of dislocation and cracks (Lee et al. 2015). When large-scale production begins, property variation and the potential for structural failure are expected to increase due to the variability in material used, design errors, and manufacturing errors. Determining the acceptable level of design values should measurably increase the reliability and safety of structures (Wencheng 2011). Therefore, furniture joints must resist external loads by utilizing such design values. At this point, a source of difficulty for designers and engineers lies in estimating the failure probability for structures and making appropriate reliability analyses (Echard et al. 2014).

In a previous paper (Eckelman et al. 2016), the use of statistical lower tolerance limits when determining reasonable design values for mortise and tenon joints was explored. The results of the study indicated that this is a useful approach that provides information needed to rationally determine design values. Of particular interest, the study allows designers to relate the fraction of the average value with the degree of confidence used for design purposes. Therefore, the question arises whether a statistical lower tolerance limit approach could also be used to determine reasonable design values for two-pin moment-resisting dowel joints.

The aim of this study was to examine the estimation of reasonable design values for two-pin moment-resisting dowel joints by using the lower tolerance limits (LTLs) method. In doing so, the goal was to obtain initial insight into appropriate confidence/proportion levels for one configuration of two-pin moment-resisting dowel joints, as well as understanding of the relationship between LTLs and sample size.

EXPERIMENTAL

Materials and Specimen Construction

The construction of the specimens used in this study is shown in Fig. 1. The red oak (Quercus rubra) and white oak (Quercus alba) materials used in specimen construction were obtained from a local sawmill. A single meter-long board was cut from the end of each full-length board obtained for the study. These meter-long boards were conditioned to 7% moisture content and then machined to a thickness of 22.225 mm. Blanks, 63.5 mm wide by 305 mm long, were then machined from these meter-long board and numbered sequentially. The defect-free rails and posts were then randomly selected from this pool of material. Plain red oak dowels (Quercus rubra), averaging 9.4 mm in diameter by 50.8 mm in length, were used in the construction of the specimens.

Fig. 1. Rail configuration. Measurements are given in mm.

Holes were drilled in the rails and posts to a depth of 25.4 mm using a 9.4 mm diameter router bit. The tolerances were 0.05 mm between the surface’s end and the dowel hole wall. The hole walls and half the length of each corresponding dowel were coated with 40% solid content polyvinyl acetate (PVA) adhesive (Franklin International, Columbus, USA). The coated end of each dowel was then inserted into the accompanying rail hole to a depth of 25.4 mm. After the rail components cured for 8 h, the post holes and the exposed dowel surfaces were coated with adhesive. The dowels were then inserted into the holes at the edge of the posts, and the resulting assembly was clamped together for 8 hours. All specimens were subsequently maintained at 7% moisture content.

Determination of the Mechanical Properties of the T-shaped Joints

All tests were conducted on an MTS universal test machine (MTS Systems Corp. Minneapolis, MN, USA). Specimens were held for testing as shown in Fig. 2. The vertical rate of load head movement was 12.7 mm/min. Loads were applied to the rail at a point 0.254 m from the post. Tests were continued until a non-recoverable drop-off in the load occurred (Erdil et al.2005).

Fig. 2. Vertical static loading test set-up

The following expressions were used to calculate bending stresses, shear stresses, and axial stresses of the joints (Eckelman 1971; Hibbeler 2014):

For bending stress,

Where is normal stress due to bending (MPa), F₄ is bending moment capacity (N.mm), P is ultimate load (N), l is moment arm (mm), ȳ is the distance between center of the rails and the surface of the dowel loaded in compression (mm), I_T is total moment of inertia of the dowels (mm⁴), I₁ is moment of inertia of the dowel loaded in tension (mm⁴), I₂ is moment of inertia of the dowel loaded in compression (mm⁴), r is radius of dowels (mm), A₁andA₂are areas of the dowels loaded in tension and compression (mm²), respectively. The parameters d₁ and d₂are distances between the rail center and the centerlines of the dowels loaded in tension and compression (mm), respectively, and y₁ and y₂ are distances between the dowel centerlines loaded in tension and compression, respectively, and the outside of the dowel loaded in compression (mm).

Fig. 3. Configuration of dowels on the cross-section of rail

For shear stress,

where τ is shear stress on the dowel loaded in tension (MPa), F_v is shear force on all dowels (N), b is the dowel diameter (mm), and Q is centroid area of dowel in tension (mm³).

For axial stress,

Where is normal stress due to dowel withdrawal (MPa), F₂ is axial force on dowel in tension (N), and d₃ is the distance between dowels in compression and the outside compression rail edge (mm).

Determination of the Lower Tolerance Limits

A normality assumption for a data set must be shown to make reliable tolerance analyses before calculating tolerance limits. If a distributional assumption were not made, tolerance analysis would be damaged. If data are normally distributed, then univariate/ multivariate tolerance analyses must be taken into consideration. Otherwise, occasionally, data may not be close to normal. In this case, researcher may not wish to make any distributional assumption and non-parametric tolerance intervals can provide an answer to obtain lower tolerance limits (Young 2010).

For design purposes, statistical lower tolerance limits for normal distribution enable a designer to apply test results to the performance one can expect from similar joints in practice—with a specified degree of confidence. These limits are defined by the expression,

where, LTL refers to the lower tolerance limit for a set of test data, X̄ refers to the average capacity of the test results, s refers to the standard deviation of the results, and k is a tolerance factor “such that the probability is γ that at least a proportion β of the distribution will be greater than X̄ – (k_{(n, γ, β)}s), based on a sample size of n” (Natrella 1963).

Tolerance factors, which are a function of chosen sample size and confidence/proportion levels, can be obtained from a number of published sources (Lieberman 1957; Natrella 1963); moreover, they may also be calculated using the expression given by Link (1985), and again later provided in the R-tolerance package by Young (2016).

An important question when using statistical lower tolerance limits to establish reasonable design values for joints used in furniture construction is to recommend what confidence/proportion level is most appropriate for furniture construction. A secondary question of importance involves the sample size needed to establish the data base on which the selected level is based. Sample size determination for univariate normal distribution, based on specified tolerance intervals, was developed by Faulkenberry and Weeks (1968). Young et al. (2016) proposed a procedure on determining sample size for normally distributed data sets by modifying the Faulkenberry-Weeks method.

In the case of non-normal distributed data sets, non-parametric tolerance limits are calculated by means of the following binominal probability expression (Young 2010),

where X_i represents the values below LTL value, is the LTL value, is the significance level (α = 1- γ), n is the sample size, x is the number of samples below the LTL value, p is proportional level (β), and q is one minus the proportion level (1-β).

RESULTS AND DISCUSSION

Sample Size Determination for Normally Distributed Datasets

In the pilot study, according to Central Limit Theorem (CLT), 30 T-shaped edgewise two pin moment-resisting dowel joints, constructed of red oak and white oak, were used as reference data to determine sample sizes using the modified Faulkenberry-Weeks method. The results of these data sets are shown in Table 1. In order to check normality of the data sets, Shapiro-Wilks tests were done for both sample groups. The test do not rejects the null hypothesis (H₀: Dataset is normally distributed) when it is insignificant (p-value>0.05). Therefore test allows to indicate that data fits the normal distribution with 95% confidence (Ghasemi and Zahediasl 2012).

Table 1. Results of the Datasets for 30 T-shaped Joints

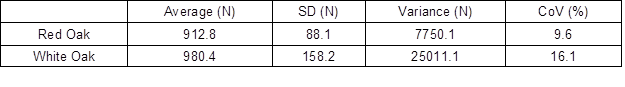
The Shapiro-Wilks normality test shows that p-values for joints constructed of red oak and white oak are 0.061 and 0.236, respectively. Both p-values are greater than 0.05, classifying the data sets as normally distributed, and the proposed methods could be used to determine sample sizes by using the pilot study specimens. Moreover, the lower specification limits were chosen as the reference data mean minus 3σ, due to a classic rule-of-thumb used for setting specification limits, namely, to take +/- 3 standard deviations from the mean of a reference sample (Young et al. 2016). Minimum samples sizes for corresponding confidence/proportion levels are shown in Fig. 4. Identical sample sizes were obtained for both data sets. The minimum sample size requirements increased with higher confidence/proportion levels. Therefore, 220 specimens were constructed for each joint group to analyze LTLs at 75/75, 90/75, 75/90, 90/90, 95/90, 90/95, 95/95, 99/95, 95/99, and 99/99 confidence/ proportional levels.

Fig. 4. Minimum sample size requirements corresponding confidence/proportion levels

Ultimate Load Capacity of the T-shaped Joints

Results for the joint specimens constructed of red oak are illustrated in Fig. 5. The average ultimate load capacity was 948.1 N, with a standard deviation of 120.6 N and a coefficient of variance (CoV) of 12.7%. The highest and the lowest load capacity levels were 1298.9 N and 631.6 N, respectively.

Fig. 5. Ultimate load capacity of T-shaped joint constructed of red oak

Results of the joint specimens constructed of white oak are illustrated Fig. 6. The average ultimate load capacity was 958.4 N with a standard deviation of 146.1 N and a CoV of 15.3%. The highest and lowest load capacities were 1343.4 N and 573.8 N, respectively.

Fig. 6. Ultimate load capacity of T-shaped joint constructed of white oak

The Shapiro-Wilks test (Table 2) shows that the white oak data set was normally distributed (p-value = 0.5992 > 0.05), whereas those of red oak were not normally distributed (p-value = 0.0081 < 0.05). The normality assumption may be violated due to data set outliers (Fig.7). Therefore, LTL values of white oak specimens were calculated using the expression , whereas those of red oak specimens were calculated using binomial probability.

Table 2. Shapiro-Wilk Normality Test for Data Sets

Fig. 7. Boxplots and histogram graphs for a: specimens constructed of white oak b: specimens constructed of red oak

Lower Tolerance Limits of Joint Specimens

The parameters indicated in Eqs. 1 to 11 are shown in Table 3. In respect to the calculations in these equation, results of the LTL values of joints corresponding to bending, shear, and axial stresses are given in Table 4.

According to the results, the LTL value of joints constructed of white oak for bending stress were 118.7 MPa at the 99/99 level. Those of shear stress and axial stress were 2.28 MPa and 61.1 MPa, respectively (Table 4). Ratios of LTL value at 99/99 level and the mean were approximately 59.4%, and there is no specimen below this LTL value. On the other hand, those of red oak are 130.7 MPa, 2.51 MPa, and 67.2 MPa, respectively. Approximately 66.1% of the mean is equal to the LTL value at a 99/99 level. Besides, there were no specimens under the LTL value. Considering this information, it might be concluded that the LTL value of specimens is equal to approximately 2/3 of the average strength.

Table 3. Dimensional Parameters for Stresses

Discussion

LTL methods provide such information that % of the future products would have (1-)% failure probability. That is, the given LTL value would result in reasonable design values, suggesting that stress on the joints should not be exceeded to reduce the product’s failure probability when subjected to external loads such as PN-EN 1728 (2012), PN-EN 1729-2 (2006) (Smardzewski 2015). The joints are designed by using LTL values at desired confidence/proportion levels. In doing so, first the dowel diameter must be determined corresponding to bending, shear, and axial stress shown in Eqs. 1 to 11. The length of the dowels is determine by using following expression (Eckelman 1971),

(14)

where F₂ is withdrawal strength, D is dowel diameter, L is dowel length, S₁ is shear strength of wood member, S₂ is shear strength of dowel, a is adhesive factor, b is dowel tolerance fit factor, and c is dowel surface factor. (The calculation does not fit with the metric system because of its coefficients, so all parameters should be considered in pound-inch system, then results should be converted to metric system.)

Assuming a side frame constructed of either red oak or white oak is subjected to vertical and horizontal external loads according to PN-EN 1728 (2012), PN-EN 1729-2 (2006), the cross-section of the post, stretcher, and rail are shown in Fig. 8. The frame was structurally analyzed using the stiffness (displacement) method, and the bending moment capacity of the side rail to back post joint was 120.6 Nm, while those of shear force were 796.8 N. When using two-pin moment resisting red oak dowel joints on side frames also constructed of red oak, the bending, shear, and axial stresses should not exceed 130.7 MPa, 2.51 MPa, and 67.2 MPa for the side rail to back post joints, respectively. Those frames made of white oak resulted in 118.7 MPa, 2.28 MPa and 61.1 MPa, respectively. Accordingly, the minimum sizes of dowel diameter and length are given in Table 5.

Table 4. LTL Values, Ratio of LTL Value and Mean, and Percent of Specimens below LTL Value for Joints Constructed of White Oak and Red Oak at Specified Confidence/Proportion Levels

Table 5. Minimum Dowel Diameters According to Bending, Shear, and Axial Stress, and Minimum Dowel Length Requirement Corresponding to LTL Value at 99/99 Level

*Tabulated values of shear strength are 12,300 MPa and 12,500 MPa for red oak and white oak at 12% moisture content, respectively (FPL 2010). Those of 7% moisture content are (S₃x [1+0.03*(12-7)]) (Eckelman 2003).

Fig. 8. Configuration of chair side frame and, cross-section of rail, post and stretcher (in mm)

The largest diameters (12 mm for red oak and 13.1 mm for white oak) were obtained in the shear strength. Those diameters must be chosen such that the dowel joints survive under any internal forces when subjected to an external load, as shown in Fig. 8. Correspondingly, dowel lengths were 31.5 mm for red oak and 28.5 mm for white oak when the parameters in Table 5 were plugged into Eq. 14. The given dowel sizes are the minimum requirements according to the external loading in Fig. 8, and theoretically provide 1% failure probability on the side rail to back post joint of chair frames for 99% of the future products.

Probabilistic approaches, such as tolerance intervals, would ensure the reliability of a structure. Regardless of how one sets safety factors using the deterministic approach, probabilistic approaches (reliability analysis) provide more precise and effective results; however, the failure probability never become zero (Papadrakakis et al. 1996, Sediva et al. 2010). Bearing in mind such information, the lower tolerance limits, which determine the reliability and safety of products, would provide a systematic procedure and an insight to determine reasonable design values for furniture joints. However, such procedures must be conducted with design standards identical to this experiment to get homogeneous data. Otherwise, a designer might fail to obtain reliable results.

CONCLUSIONS

The design values for two-pin moment resisting dowel joints were estimated using calculated LTL values because one-sided tolerance limits are used to determine the reliability and safety of products.
Sample sizes for tolerance analysis were determined using modified Faulkenberry-Weeks methods. The minimum sample size requirement for such studies was 215 at the 99/99 confidence/proportion level. Larger sample sizes are needed for higher confidence/proportion levels.
The results provide definitive answers as to what failure probability joints, designed by using given LTL values, would have after loads were imposed on a chair. To produce more reliable chairs, LTL values at the higher confidence/proportion levels must be used.
To produce reliable furniture, recommended stress levels on chair joints constructed of white oak should not exceed 118.7 MPa, 2.28 MPa, and 61.1 MPa at the 99/99 level in bending, shear and axial, respectively. Joints made of red oak should not exceed 130.7 MPa, 2.51 MPa, and 67.2 MPa, respectively.

ACKNOWLEDGEMENTS

This study was supported by the USDA National Institute of Food and Agriculture, Forest Service, Ministry of National Education of the Republic of Turkey, and Wood Research Laboratory at Purdue University.

REFERENCES CITED

Derikvand, M., and Ebrahimi, G. (2015). “Rotational stiffness of L-shaped dowel,” in: Proceeding of the 27th International Conference, Research of Furniture Industry, Ankara, Turkey.

Echard, B., Gayton, N., and Bignonnet, A. (2014). “A reliability analysis method for fatigue design,” International Journal of Fatigue 59, 292-300. DOI: 10.1016/j.ijfatigue.2013.08.004

Eckelman, C. A. (1971). “Bending strength and moment-rotation characteristics of two-pin moment resisting dowel joints,” Forest Products Journal 21(3), 35-39.

Eckelman, C. A. (1974). “Reasonable design stresses for woods used in furniture,” Purdue University Agricultural Experiment Station Research Bulletin 916, 1-7.

Eckelman, C. A., Erdil, Y. Z., and Zhang, J. (2002). “Withdrawal and bending strength of dowle joints constructed of plywood and oriented stranboard,” Forest Products Journal 52(9), 66-74.

Eckelman, C. A. (2003). Textbook of Product Engineering and Strength Design of Furniture, Purdue University, West Lafayette, IN, USA.

Eckelman, C. A., Erdil, Y. Z., and Haviarova, E. (2003). “School chairs for developing countries: Designing for strength and durability, simplicity and ease of construction,” Forest Products Journal 53(2), 1-8.

Eckelman, C. A., Uysal, M., and Haviarova, E. (2016). “Statistical lower tolerance limits for rectangular mortise and tenon joints,” BioResources 11(3), 7162-7171 DOI: 10.15376/biores.11.3.7162-7171

Erdil, Y. Z., Kasal, A., and Eckelman, C. A. (2005). “Bending moment capacity of rectangular mortise and tenon furniture joints,” Forest Products Journal 55(12), 209-213.

Faulkenberry, G. D., and Weeks, D. L. (1968). “Sample size determination for tolerance limits,” Technometrics 10(2), 343-348.

Forest Products Laboratory (FPL) (2010). Wood Handbook: Wood as an Engineering Material, U.S. Department of Agriculture, Forest Products Laboratory, Madision, WI, USA.

Hibbeler, R. C. (2014). Textbook of Mechanics of Materials, Prentice Hall, Pearson, NJ, USA

Ghasemi, A., and Zahediasl, S. (2012). “Normality tests for statistical analysis: A guide for non-statisticians,” International Journal of Endocrinology and Metabolism 10(2), 486-489. DOI: 10.5812/ijem.3505

Lee, Y. L., Makam, S., McKelvey, S., and Lu, M. W. (2015). “Durability reliability demonstration test methods,” Procedia Engineering 133, 31-59. DOI: 10.1016/j.proeng.2015.12.621

Link, C. L. (1985). “An equation for one-sided tolerance limits for normal distributions,” Statistician, United States Department of Agriculture: Forest Service-Forest Products Labarotory, Madison, WI (FPL 458), 1-4.

Natrella, M. G. (1963). National Bureau of Standards Handbook 91: Experimental Statistics, U.S. Government Printing Office, Washington, D.C., USA.

Papadrakakis, M., Papadopoulos, V., and Lagaros, N. D. (1996). “Structural reliability analyis of elastic-plastic structures using neural networks and Monte Carlo simulation,” Computer Methods in Applied Mechanics and Engineering 136(1-2), 145-163. DOI: 10.1016/0045-7825(96)01011-0

PN-EN 1728 (2012). “Furniture. Chairs and stools. Determining strength and durability,” Polish Committee for Standardization, Warsaw, Poland.

PN-EN 1729-2 (2006). “Furniture. Chairs and tables for educational institutions. Part 2: Safety requirements and methods of testing,” Polish Committee for Standardization, Warsaw, Poland.

Sediva, B., Wagnerova, E., Vavra, F., Toupal, T., and Marek, P. (2010). “Statistical monitoring of failures – Methods and use,” in: Proceedings of the 11th International Scientific Conference Electric Power Engineering, Brno, Czech Republic.

Smardzewski, J. (2015). Furniture Design, Springer, Cham, Switzerland. DOI: 10.1007/978-3-319-19533-9

Tas, H. H. (2010). “Strength properties of L-profiled furniture joints constructed with laminated wooden panels,” Academic Journals 5(6), 545-550.

Wencheng, L. (2011). “Principles for determining material allowable and design allowable values of composite aircraft structures,” Procedia Engineering 17, 279-285. DOI: 10.1016/j.proeng.2011.10.029

Yerlikaya, N. C. (2014). “Investigation of optimum dowel spacing for corner joints, which are reinforced with glass-fiber fabric in case-type furniture,” Wood Research 59(1), 191-200.

Yerlikaya, N. C., and Aktas, A. (2013). “Enhancement of T-joints of spruce wood reinforced by using glass-fiber composite laminate,” Academic Journals 8(13), 515-523. DOI: 10.5897/SRE12.681

Young, D. S. (2010). “Tolerance: An R package for estimating tolerance intervals,” Journal of Statistical Software 36(5), 1-39. DOI:10.18637/jss.v036.i05

Young, D. (2016). “Normal tolerance interval procedures in the tolerance package,” The R Journal 8(2), 200-212. ISSN 2073-4859

Young, D. S., Gordon, C. M., Zhu, S., and Olin, B. D. (2016). “Sample size determination strategies for normal tolerance intervals using historical data,” Quality Engineering 28(3), 337-351. DOI: 10.1080/08982112.2015.1124279

Zhang, J. L., and Eckelman, C. A. (1993). “The bending moment resistance of single-dowel corner joints in case construction,” Forest Products Journal 43(6), 19-24.

Article submitted: February 2, 2018; Peer review completed: April 1, 2018; Revised version received: April 19, 2018; Accepted: April 21, 2018; Published: May 22, 2018.

DOI: 10.15376/biores.13.3.5241-5253