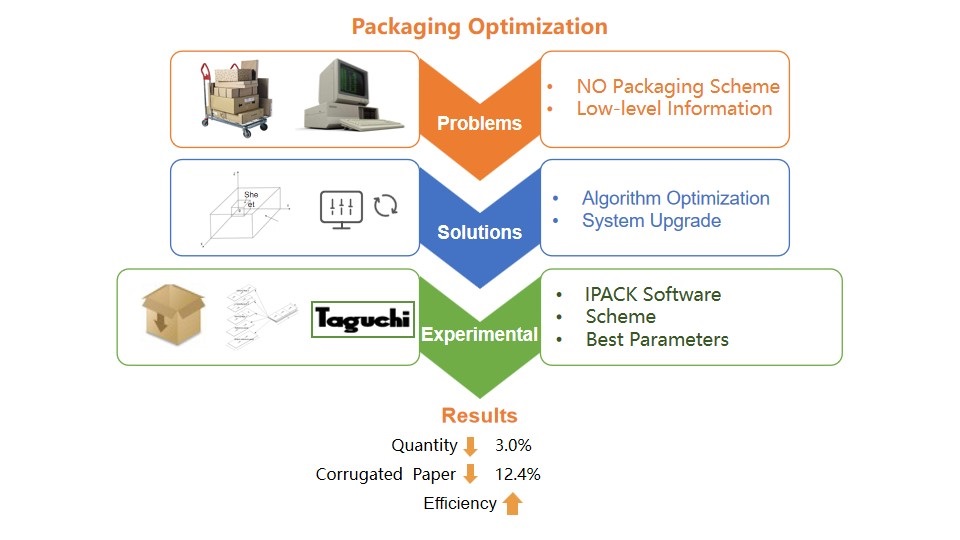
Research on packaging optimization in customized panel furniture enterprises

Wang, G., Zhu, J., Cai, W., Liu, B., Tian, Y., and Meng, F. (2021). "Research on packaging optimization in customized panel furniture enterprises," BioResources 16(1), 1186-1206.

Abstract

Various information systems have been implemented in most of the customized panel furniture companies in China, resulting in increased production difficulty and informational isolation. Enterprises need to adopt more systematic, scientific, and information-based methods to guide the production on the shop floor. Packaging optimization is important because it promotes sustainable development in furniture enterprise. Through the examination of the packaging process in customized panel furniture companies, this study investigated the bottleneck problems of the packaging process, which are predominantly focused on the calculation of the optimal packaging scheme and the upgrade of information systems. After exploring the theories and methods to solve the existing bottleneck problems, the heuristic algorithm was applied to obtain the optimal packaging schemes and complete the upgrade of packaging process information system. Based on the intelligent packaging software in company A, the Taguchi method was applied to find the best optimization parameters, which was proven effective in comparison with the original packaging solution. The number of packaging was decreased by 3.0%, and the amount of packaging corrugated paper decreased by 12.4. The packaging efficiency represented by the total packaging time showed a significant improvement despite the unit packaging time having increased by 2.0%.

Download PDF

Full Article

Research on Packaging Optimization in Customized Panel Furniture Enterprises

Guokun Wang,^a Jiangang Zhu,^a,* Wenwen Cai,^a Bin Liu,^a Yubin Tian,^a and Fanyang Meng ^b

Keywords: Panel furniture enterprise; Packaging optimization; Heuristic algorithm; Informatization; Taguchi method; Stopwatch research method

Contact information: a: College of Furniture and Industrial Design, Nanjing Forestry University, Nanjing 210037, China; b: College of Materials Science and Engineering, Northeast Forestry University, Harbin 230100, China; *Corresponding author: austin_zhu@njfu.edu.cn

GRAPHICAL ABSTRACT

INTRODUCTION

With the development of information technology and the continuous reduction of the threshold of information systems, various types of information systems are gradually being adopted by furniture manufacturing enterprises (Ratnasingam et al. 2019; Xiong et al. 2020). Under the background of the development of “Internet+”, “Industry 4.0” and “Made in China 2025”, industrialization and informatization are gradually merging (Ray et al. 2017; Ratnasingam et al. 2020). However, this practice can lead to increased production difficulty, informational isolation, and process barriers (Yang et al. 2013). Packaging optimization can effectively promote the sustainable development of enterprises. Optimizing packaging can improve product quality, reduce the proportion of fillers, save packaging and transportation costs, reduce warehouse storage space, and reduce the number of times of transportation.

Packaging optimization can be carried out from the aspects of packaging material, packaging structure, packaging operation method, packaging algorithm, etc.

Guo et al. (2015) used an aqueous mixture of corn starch, straw fiber, and foaming agent to prepare a biomass cushion packaging material in a heated mould. The optimal forming parameters were obtained through experiments. After comparing with the mechanical performance of expanded polyethylene and expanded polystyrene, it was concluded that biomass cushion packaging materials can replace current packaging materials.

Pan et al. (2014) used ANSYS software to simulate the phone packaging box. By calculating the force distributions of the packaging box and optimizing the structure, the optimal buffer structure was obtained. After comparing the theoretical simulation results with the measured results, it was concluded that the simulation experiment has certain guiding significance.

In the furniture manufacturing industries, there are some risk factors in the packaging process that may lead to work-related diseases. Colim, etc. conducted investigations and evaluations from the perspective of ergonomics. It was concluded that the use of robot aids equipment can help reduce the probability of disease (Colim et al. 2020).

Chen et al. (2013) solved the problem that some small rectangles needed to be packed into a fixed rectangular object by developing a rectangular layer-packing algorithm (RLPA) combined with modified genetic algorithm (GA) or particle swarm optimization (PSO) algorithm. Through the experiments, the effectiveness of the improved algorithm was verified.

In this paper, the problems and solutions of the panel furniture companies were explored. The solutions were applied to Company A. The packaging optimization was accomplished by using intelligent packaging software, and the Taguchi method was applied to find the best optimization parameters. After verification and evaluation, it was concluded that Company A had successfully completed packaging optimization. Finally, the theory and method suitable for solving the bottleneck problems of packaging optimization in general panel furniture enterprises were summarized.

Problems

The packaging process is the last step in the production process of panel furniture, which is largely occupied with the packing of the finished panels in accordance with certain rules to ensure that the panels can be safely delivered to customers without damage. The packaging rules are the experience summarization of a company to guide the packaging workers in a simple operation. Lacking scientific and effective information to guide the operation, the packaging process usually depends on manual operation. The consequence is the inferior informatization level of the packaging process or even complete separation of the existing information system of the enterprise. The calculation of the optimal packaging scheme and the informatization upgrading of the packaging process have become the bottleneck of the packaging process in panel furniture companies (Nicola 2010; Schaefe et al. 2018).

Packaging scheme

Manual packaging is commonly used in most panel furniture enterprises. A small number of enterprises have stand-alone equipment such as paper cutters and sealing machines. Just a few enterprises have automatic packaging lines (Jin et al. 2016). The main business of panel furniture companies is customized services, resulting in different sizes of panel parts, so it is impossible to form a unified paradigm of packaging.

A packaging scheme refers to the overall scheme design to guide the packaging operation according to the size and type of the product. At present, most enterprises formulate corresponding packaging rules based on their product processing routes, panel size, panel name, panel type, and workers personal packaging experience, which makes the quality of packaging in aspects of quantity, weight, filling rate, etc. completely determined by the worker’s operation and raising uncertainty (Denni et al. 2011).

The rule-based software has been adopted to automatically calculate the packaging scheme, so that the packaging workers can obtain subcontracting information automatically and perform the packaging operation according to the packaging scheme. More importantly, furniture enterprises can achieve effective guidance on packaging operations and greatly reduce their dependence on workers. Unfortunately, the proprietary software is far from operating at its proper capacity. For example, most companies can set only simple rules, such as maximum package weight, maximum package height, etc. The relatively simple packaging solution generated is hardly the optimal solution, not to mention reducing the number of packaging, packaging materials and fillers, and saving transportation costs (Popa et al. 2015).

Packaging Information

Packaging information is composed of subcontracting information, packaging weight, packaging height, number of panels in the package, and placement position of panels in the package. Such data are generated according to the packaging scheme formulated by the size, process route, product characteristics, production line layout, etc. At the moment, most companies only can handle basic packaging information about the number of panels in the package and the total weight of the package.

With the continuous introduction and updating of automatic packaging equipment such as manipulators, paper cutters, box sealing machines, etc., more packaging information is required. It is necessary to know the size of the package, the location of the panels in the package, and the weight of the package in advance. Therefore, to achieve the guidance of the packaging operation effectively, enterprises must first formulate a reasonable and easy-to-maintain packaging scheme, which is capable of breaking the informational isolation and enabling the packaging information to integrate with the entire information system (Liu and Li 2015).

The bottleneck of the packaging process is the calculation of the optimal packaging scheme and the informatization upgrading of the packaging process. There are relatively few studies on the optimal packaging of panel furniture companies, and the packaging methods with complete information source and concise packaging instructions on the production site are relatively insufficient. To thoroughly solve the bottleneck problem of the packaging process, the optimization of packaging must be conducted from the very beginning by refining the optimal packaging scheme and upgrading the information of the packaging process.

Optimal Packaging Solution

The calculation of the optimal packaging scheme is a typical NP-hard problem. Because the NP-hard problem is very complex and has great application value, it has become the focus of research in today’s academia. Constructive heuristic algorithm is a commonly used method to solve the packing problem. This section will study the algorithm of the optimal packaging scheme based on the constructive heuristic algorithm (Nguyen and Kim 2013).

Constructive heuristic algorithm

A constructive heuristic algorithm is a constructed algorithm based on manual loading experience. The algorithm is highly targeted, so the calculation efficiency of the algorithm is very high. The quality of the algorithm depends on the design of the loading strategy. The person who designs the algorithm must be very familiar with the problem to be solved. Through constructive heuristic algorithms, it is often possible to obtain a more reasonable loading scheme than manual loading. However, if the loading strategy is unreasonably obtained, the results may not be satisfactory. Therefore, in the actual construction of the packaging algorithm, it is necessary to continuously optimize the loading strategy based on experience (Yang 2016; Feng et al. 2005).

George and Robinson (2015) introduced the concept of “layers” in the packing problem, that is, loading one layer at a time along one side of the loading box during the packing process. When loading in each layer, it is loaded according to the rules established in advance, and the three-dimensional packing is converted into two-dimensional packing through the layer loading method, which effectively reduces the packing complexity (Alvelos et al. 2009). Because the thickness of the parts of the panel furniture is mostly uniform, when designing the algorithm, the concept of layers can be introduced to reduce the complexity of the algorithm.

Algorithm design

The design of the algorithm must be carried out on the basis of satisfying the constraints of packing (Mayer et al. 2020). The following constraints should be met during the packing of the panel:

● Order constraint, during the packing process, the single order should be used as the dimension for packing.

● Panel type constraints, different types of panels should be packed according to different packing rules according to the actual situation of the enterprise itself.

● The size of the bottom layer is constrained. The lowest panel in the box must be a single panel, and it should be the largest panel in a single package.

● The direction in which the panels are placed is constrained. When the items are placed, their sides should be parallel to the packaging box.

● The weight of the loading box is constrained, where the total weight of the panels in the loading box cannot exceed the maximum load set by the loading box.

● The height of the panels in the loading box is restricted, where the total height of the panels in the loading box cannot exceed the height limit.

An excellent loading strategy can greatly increase the calculation efficiency of the algorithm, which makes it easier to obtain a better loading scheme (Wang 2019). For the packing of panel furniture, the following loading strategies are summarized:

● Sort the panels by the weight, where the heavier panel will be placed first. The weight of the panel is proportional to the volume, and the heavier one is also larger, which is suitable for being placed at the bottom. If the smaller panel is placed underneath, it is not conducive to stabilizing the center of gravity of the package, nor to the managing reasonably of fragmented space.

● Place the panel in the order first at a corner of the loading box space. According to the Cartesian three-dimensional coordinate system, load the starting angle to select the coordinate origin.

● Take the largest bottom panel in the package as the reference panel, find the ratio of the panel to be loaded and the reference panel, sort these ratios, and then find the panels with the ratio of 1.0 or close to 1.0 to combine them. If the new panel meets the loading constraints, keep the new panel for subsequent loading, otherwise discard it. In this way, small-sized panels can be spliced at the same level, reducing the number of packages.

● When selecting panels for loading, try to avoid the occurrence of fragmentary space after loading, and select panels that make the remaining space neat for loading.

● When placing the panel, there are two placement methods, namely, the long side of the panel is placed parallel to the long side of the loading box and the long side of the panel is placed parallel to the short side of the loading box.

● When the initial remaining space is quite large, the division of the remaining space cannot be avoided by loading another panel, so try to choose a larger panel for loading.

Panel packing steps

The workflow of packing the panels based on structural heuristic algorithm is shown in Fig. 1. This workflow is a processing process that is applicable to one order and one rule. Other orders and rule processing processes can refer to this workflow.

Fig. 1. Constructive heuristic algorithm flowchart

The constraints and strategies of heuristic algorithm are constructed based on manual packing experience, which can solve the problem of the onboard packing of furniture and optimize the results of panel packing to a certain extent. But this algorithm has certain disadvantages. The algorithm is designed under the assumption that the thickness of the panel is consistent, and it is only suitable for packaging schemes with the same thickness. Moreover, the area utilization rate is not considered in the constraints, which may result in a low area utilization rate of a certain layer. In the loading strategies, the panels were combined and loaded according to the ratio, but the specific lower limit of the ratio was not given, which needs to be determined according to the specific situation. The calculation of the optimal packaging scheme focuses on improving the cubic utilization rate of packaging, reducing the use of packaging materials and fillers, and thereby reducing the packaging and transportation costs of products, which is of great significance to the rapid development of furniture industry.

Informatization Upgrading Solution

The bottleneck problem in the informatization upgrading of the packaging process lies in the disconnectedness between the packaging information calculated by the packaging scheme and the production equipment, which results in over depending on the experience of the packers.

The calculation of packaging schemes is closely bound up with the upgrade of information technology. The scientific packaging scheme depends on the source of information, and the perfect information system is the guarantee for the implementation of the optimal packaging scheme. In order to achieve the informatization upgrading, the calculated packaging information needs to be able to connect with the existing information system of the enterprise, where the data can be transmitted through Web Service or intermediate database. The packaging information, with more details in packaging size, filler size, and weight for manual packaging, can be transmitted to the automatic sorting line and automatic packaging line. Only by implementing the informatization upgrading is it possible to better achieve the packaging optimization in panel furniture enterprises.

EXPERIMENTAL

Company A mainly engaged in customized panel furniture production. The optimization and upgrading of the packaging process of company A were conducted with an aim to improve the competitiveness and achieve sustainable development of enterprises. Due to the imperfect informatization in its packaging process, only simple subcontracting information was applied to guide the sorting operation. The bottleneck problem of its packaging optimization lay in the inability to automatically calculate the packaging schemes based on existing process routes and packaging rules, bringing the automatic packaging lines cannot obtain packaging information.

Company A designed new packaging rules based on the existing process routes, and issued the rule amendments by upgrading the company’s existing order splitting software – Easym, which can automatically calculate the packaging schemes. However, the packaging schemes of Company A can only subcontract according to the name of the panels on the basis of limiting the weight of the packages and the number of the panels. Unreasonable packaging such as super high and overweight often occurred. Moreover, the packaging information could not be automatically transmitted to the automatic packaging equipment, and it needed to be uploaded manually by personnel.

To resolve the issue, the intelligent packaging software-IPACK software was introduced to company A. The software not only can calculate different schemes according to the existing process routes and packaging rules of the enterprise, and automatically check whether the packaging is reasonable, but also it can be seamlessly connected with the existing information system of the enterprise, which can provide data sources for automatic packaging equipment and provide accurate packaging guidance for on-site production (Bambura et al. 2020).

IPACK Software

IPACK software is a kind of intelligent packaging software tailored to the panel furniture industry, which was developed by Guangzhou Liansi Software Technology Co., Ltd. The software can access the existing bill of materials of the furniture enterprise, pre-calculate the packaging scheme of the panel according to the predefined packaging rules, and automatically generate the packing list. More importantly, the IPACK can be connected to the enterprise’s ERP system, MES system, automatic sorting line and automatic packaging line.

Fig. 2. Splicing diagram

Based on the constructive heuristic algorithm, a packaging scheme, entitled cabinet panel splicing rule, was generated by IPACK software. The principle of cabinet panel splicing is to find qualified panels according to the packing process based on the loading strategy based on the constraints. The next step is to find a larger panel among these panels as the bottom reference panel. Then one uses the layer-by-layer stacking of panels to form the package and finally find the best solution through software calculation (Fig. 2). The splicing rules can be configured in aspects of packaging, load-bearing layer, splicing layer, top layer and merge (Table 1).

Table 1. Main Points of Splicing Rules

The setting value of each parameter in the parameter setting can be further refined. The conditions for merging are controlled by merge rules. Depending on the weight of the package or the number of panels, the method of merging can be chosen, and limit the maximum package weight and other parameters by the merging function in the parameter settings to ensure that its total weight is within the control range (Figs. 3 and 4).

Fig. 3. Parameter setting of merge rules

Fig. 4. Parameter setting of splicing rules

Another commonly used rule in IPACK software is mixed package. The principle of the mixed package rule for cabinet panels is to find the panels that meet the conditions in the packing list through the condition setting, which the parameters can be determined by the maximum weight of the single package, the maximum number of the single package, the maximum length difference, and the maximum width difference. The mixed package of panels and parts can also be combined through the merger rules to meet the qualified packaging.

Optimization Scheme

The panel splicing and mixed package in IPACK software are the two main packaging rules adopted in company A’s packaging optimization. Panel splicing rules are mainly used for cabinet body panel splicing, which uses the three conditions of weight, height and number of layers to limit. Panel mixed packaging is mainly used for small pieces, strips and backboard packaging. After the calculation is completed, the software will automatically generate the completed packaging schemes and transfer the data to the enterprise’s MES system through the SQL database, which realizes the connection with the enterprise’s existing information system.

By introducing IPACK software and restricting the use of packaging rules, company A solved the problem of non-automated calculation in the packaging solution. At the same time, the informatization upgrading in company A is realized by connecting the IPACK software to the existing database of the enterprise, which can transmit data to the equipment and guide the work of the workers at the production site.

Best Optimization Parameters

The reduction in the number of packages directly means the reduction of logistics costs, while the increase in the volume ratio directly means the reduction of the fillers in the packages. These two points have a greater impact on the economic benefits of enterprises in the packaging process (Zhang 2011). The goal of this optimization experiment is to achieve the least number of packages after optimization and the highest volume ratio of the panels in the package.

Because the weight and height of packaging are restricted in company A, the number and volume ratio of packaging are mainly affected by the four variables as the maximum percentage of the splicing layer gap, the maximum percentage of the top layer gap, the maximum percentage of the merged splicing layer gap, and the maximum percentage of the merged top layer gap.

Because the change of the quantity and volume ratio of packaging is affected by the above four variables. Furthermore, each variable is independent of each other. The multifactorial optimization makes the traditional exhaustion method no longer adequate for solving the solution, so the Taguchi orthogonal experiment method will be applied to find the optimal parameters (Chauhan et al. 2018).

Taguchi orthogonal experiment

The Taguchi orthogonal experiment method can effectively solve the problem of an inordinate number of samples and reduce the time to find a solution greatly, which can achieve the similar effects as the exhaustive method (Manigandan et al. 2020). The first step of the Taguchi orthogonal experiment method is to select the control factor and the level of the control factor. Therefore, the maximum percentage of the splicing layer gap, the maximum percentage of the top layer gap, the maximum percentage of the merged splicing layer gap and the maximum percentage of the merged top layer gap are named A, B, C, and D, respectively. Combined with the technician’s experience of Liansi software and the requirements of company A, the level value of each control factor is formulated (Table 2).

Table 2. Values of Each Control Factor Level

The second step is to establish the Taguchi method orthogonal test table. The selecting of the correct orthogonal table and establishing the corresponding parameter combination are the key to the success of the Taguchi method. According to the number of control factors and the number of levels of control factors in this optimization experiment, the L₉ (3⁴) orthogonal table can be selected, and nine sets of orthogonal data can be obtained as shown in Table 3.

Table 3. Orthogonal Data

A total of 1000 cases were randomly selected from the above 9 sets of data for experimental calculations, and the average package quantity and average volume ratio were obtained (Table 4).

Table 4. Calculation Result

In order to count the impact of different levels of each factor on the number of packages and volume ratio, the average value X_ij of the quality characteristics of each factor at this level needs to be solved. The formula is shown in Eq. 1,

(1)

where N_i_j represents the number of experiments with the control factor i at level j, and S_i_j is the sum of the quality characteristic values of the N_ij experiments with the control factor. The value of X_ij can be calculated from the above formula, and the results are shown in Table 5.

Table 5. The Average Values of Quality Characteristic of Each Control Factors

The changes in average package quantity and average volume ratio with different values of control factors are shown in Figs. 5 and 6.

Fig. 5. Trend chart of the influence of changes in control factors on the average package quantity

Fig. 6. Trend chart of the influence of the change in control factors on the average volume ratio

To measure the difference between the average package quantity and the average volume ratio when the value of the control factor changes, the specific gravity will be calculated by the variance calculation shown in Eq. 2,

(2)

where j represents the control factor level number. m_i(S_j) is the j-th level quality characteristic value of the control factor i. m(S) is the average value of the quality characteristics of the control factor i. From the above formula, the influence proportion and percentage of different control factors on the average package quantity and average volume ratio can be obtained as shown in the Table 6.

Table 6. Ratio of the Influence of Each Control Factor on Quality Characteristics

Determine the best parameters

Because this optimization experiment is affected by multiple variables and multiple levels, the importance of each level should be comprehensively considered before the selection of factor level. At the same time, the performance of the performance index should be weighed against the large and small characteristics (Vijay et al. 2018).

By comparing the effect of the average package quantity and the average volume ratio and combining the analysis of the charts and tables, the following conclusions can be drawn:

A has a greater influence on the average volume ratio, and when A takes level 1, its average volume ratio is the highest, so level 1 can be determined by A.

B has a greater influence on the average volume ratio, and when B takes level 1, its average volume ratio is the highest, so level 1 can be determined by B.

C has a greater impact on the average number of packages, and when C takes level 1, the number of packages is the smallest, so level 1 can be determined by C.

D has a greater impact on the average number of packages, and when D takes level 1, the number of packages is the smallest, so level 1 can be determined by D.

Therefore, the final optimized parameter combination is A1, B1, C1, and D1.

After the introduction of IPACK software in company A, the optimal optimization parameters of the packaging rules were basically determined through the Taguchi method. The optimal packaging scheme was obtained and the upgrade of the packaging process information was realized. The obtained optimization solution solved the bottleneck problem of enterprise packaging optimization, but the effect of the optimization and whether it will adversely affect the company’s production capacity still needs further investigation.

RESULTS AND DISCUSSION

IPACK software was applied in Company A to complete the packaging optimization. To explore whether the optimization had a positive impact on the company’s production capacity, the effect of packaging optimization was evaluated by comparing both the number of packages and the packaging efficiency before and after optimization.

Packaging Quantity

The authors randomly selected 10,000 orders and compared the number of packages before and after optimization. Through data analysis, it was found that, on the basis of solving the existing packaging problems in company A, the overall packaging quantity was reduced by 2.96% (Table 7).

Table 7. Ratio of the Influence of Each Control Factor on Quality Characteristics

Table 8. Operation Unit Division Situation Table

Packaging Time

The comparison of packaging time was measured using the stopwatch time research method (Sembiring and Kusumawaty 2018). The worker’s packaging time was divided into five operating units, which is shown in Table 8. Based on experience and work cycle table (Table 9), the number of observations was determined to be 20.

Table 9. Work Cycle Table

Table 10. Determination of Packaging Time before Optimization

In the time measurement, a continuous test method was used. A Casio stopwatch was used to observe the five units of the packaging before and after optimization 20 times, and the actual operating time was obtained. The triple standard deviation method was applied to find and remove outliers. For the calculation of outliers, the average x and standard deviation of each operating unit were calculated as shown in Eqs. 3 and 4.

(3)

(4)

The upper limit of deviation UCL= X+3, and the lower limit of deviation LCL= X-3, those that are not in this area are outliers and should be eliminated. There were no abnormal values before and after packaging optimization (Tables 10 and 11).

The average total packaging time per package before optimization was 228.0 s, and the average total packaging time per package after optimization was 232.5 s. Single package packaging time is increased by 4.5 s, which means an increasing rate of 1.97% for packaging time after optimization.

Table 11. Determination of Packaging Time after Optimization

Packaging Production

The packaging production data of 2 months before and after optimization were randomly selected, and the average number of panels packed per person per day was counted (Tables 12). Through chart comparison (Fig. 7), it is easy to find that production efficiency has been improved, and the optimization effect is obvious.

Table 12. Average Number of Panels Packed per Person per Day

Fig. 7. Average number of panels packed per person per day

Packaging Corrugated Paper

The number of packaging corrugated paper units purchased for 10 months before and after optimization was counted, and the corresponding total number of panels was counted. By calculating the ratio of the two, it was found that the average amount of packaging corrugated paper used per panel had dropped by 12.4% (Table 13).

Table 13. Packaging Corrugated Paper Data Analysis

Evaluation

After packaging optimization, the number of packaging quantity had been reduced, but the unit packaging time had increased slightly. Under the premise that other factors had not changed, the original packaging quantity per unit time of company A was assumed to be X. As shown in Table 14, although the optimized packaging scheme increased the unit packaging time, the production capacity, instead of being reduced, had actually experienced a slight increase due to the decline in the number of packaging quantity.

Table 14. Total Packaging Time Comparison

After company A introduced IPACK software for the optimization, by comparing the four aspects of packaging quantity, packaging time, packing production and packaging corrugated paper, it was concluded that the optimized production capacity had been improved to a certain extent. Meanwhile, the bottleneck problems of packaging in company A had been solved thanks to the optimal packaging scheme under information integration.

CONCLUSIONS

The era of personalized customization has arrived. Traditional panel furniture companies must transform and upgrade to customization, and the traditional mode of manufacturing must also be transformed to intelligent manufacturing, which has been a consensus for panel furniture companies. Enterprises need to adopt more systematic, scientific, and information-based methods to guide the production on the shop floor.
Based on the analysis of the optimization points and essential nodes in the packaging process of panel furniture, it was found that the existing main bottleneck problem was the calculation of the optimal packaging scheme and the informatization upgrading of the packaging process.
Based on the heuristic algorithm, the calculation method of the optimal packaging scheme was proposed.
The upgrading of the packaging process information was the key to solve the problem of disconnectedness between the packaging information calculated by the packaging scheme and the production equipment.
Company A carried out the packaging optimization by using an intelligent packaging software and applied the Taguchi method to find the best optimization parameters. Comparing with the original packaging program, it was found that although the unit packaging time increased by 1.97%, the overall efficiency had improved because the number of packaging was decreased by 2.96%. At the same time, packaging production increased significantly, and the amount of packaging corrugated paper used for each panel dropped by 12.4%, which was a huge improvement. Company A successfully completed all-round packaging optimization.
In order to achieve the optimization and upgrading of packaging in panel furniture companies, it was important first to understand the bottleneck of the company in terms of packaging. The corresponding packaging rules should be formulated according to the company’s process route, product characteristics, production line layout, etc., and the packaging information source can be formed by exploring the best packaging scheme. Finally, on the basis of integrating the packaging information in the existing information system of the enterprise, the packaging process can realize optimization by transmitting the integrated packaging information to the equipment on the production shop floor.
Being a subject of positive significance, the optimization of packaging has long been concerned and is worthy of in-depth research. The packaging optimization in panel furniture companies was conducted in this paper with an aim to enhance the quality of the packaging, but due to the limited knowledge of the authors, the research still has to be improved for further exploration in aspects of the carton box utilization rate, the worker’s operation process, and the optimization of the packing filling volume. Furthermore, due to the space constraints, it hasn’t been explained thoroughly in the introduction of the packaging software and the comparison of the optimization effects before and after optimization.

ACKNOWLEDGMENTS

The authors are grateful for the support of the Joint Research program of Sino-foreign Cooperation in Running Schools of Jiangsu Province, China.

REFERENCES CITED

Alvelos, F., Chan, T. M., Vilaca, P., Gomes, T., Silva, E., and Valerio, D. C. (2009). “Sequence based heuristics for two-dimensional bin packing problems,” Engineering Optimization 41(8). DOI: 10.1080/03052150902835960

Bambura, R., Sujova, E., and Cierna, H. (2020). “Utilizing computer simulation to optimize furniture production system,” BioResources 15(3), 6752-6765. DOI: 10.15376/biores.15.3.6752-6765

Chauhan, N. K., Das, A. K., and Rajesha, S. (2018). “Optimization of process parameters using grey relational analysis and Taguchi method during micro-EDMing,” Materials Today: Proceedings 5(13). DOI: 10.1016/j.matpr.2018.09.029

Chen, W., Zhai, P., Zhu, H., and Zhang, Y. (2013). “Hybrid algorithm for the two-dimensional rectangular layer-packing problem,” Journal of the Operational Research Society 65(7), 1068-1077. DOI: 10.1057/jors.2013.54

Colim, A., Sousa, N., Carneiro, P., Costa, N., Arezes, P., and Cardoso, A. (2020). “Ergonomic intervention on a packing workstation with robotic aid – Case study at a furniture manufacturing industry,” Work 66(1), 229-237. DOI: 10.3233/WOR-203144

Feng, L., Xicheng, L., and Yuxing, P. (2005). “An efficient heuristic algorithm for constructing delay- and degree-bounded application-level multicast tree,” Lecture Notes in Computer Science 3795(1), 1131-1142.

George, J. A., and Robinson, D. F. (2015). “A heuristic for packing boxes into a con-tainer,” Computers Oper. Res. 7(3), 147-156. DOI: 10.1016/0305-0548(80)90001-5

Guo, A., Zhao, J., Li, J., Li, F., and Guan, K. (2015). “Forming parameters optimisation of biomass cushion packaging material by orthogonal test,” Materials Research Innovations 19(5), 521-525. DOI: 10.1179/1432891714Z.0000000001144

Jin, J. W., Chen, S. G., and Wellwood, R. (2016). “Oriented strand board: opportunities and potential products in China,” BioResources 11(4), 10585-10603. DOI: 10.15376/biores.11.4.10585-10603

Liu, S., and Li, J. (2015). “Analysis and realization of eliminate the ‘information isolated island’ in enterprise e-commerce,” in: Proceedings of the 3^rd International Conference on Mechatronics and Industrial Informatics, pp. 611-616.

Manigandan, S., Atabani, A. E., Ponnusamy, V., Pugazhendhi, A., Gunasekar, P., and Prakash, S. (2020). “Effect of hydrogen and multiwall carbon nanotubes blends on combustion performance and emission of diesel engine using Taguchi approach,” Fuel, 118120.

Mayer, B., Tadler, S., Rothenbacher, D., Seeger, J., and Wohrle, J. (2020). “A hierarchical algorithm for multicentric matched cohort study designs,” Current Medical Research and Opinion, Aug-12. DOI: 10.1080/03007995.2020.1808453

Nguyen, V., and Kim, K. (2013). “Heuristic algorithms for constructing transporter pools in container terminals,” in: 2012 IEEE Transactions on Intelligent Transportation Systems 14(2), 517-526. DOI: 10.1109/TITS.2012.2222026

Nicola, Z. (2010). Manufacturing Process Optimization within a Furniture SME, Master’s Thesis, University of Strathclyde, Glasgow, UK.

Pan, D., Qin, H., Liu, S., and Zhang, Z. (2014). “Optimal structure design of mobile phone packing box based on dynamic analysis,” Mechatronics Engineering, Computing And Information Technology (556-562), 4664-4667. DOI: 10.4028/www.scientific.net/AMM.556-562.4664

Popa, C. L., Cotet, C. E., Gavrila, S., and Ionita, V. (2015). “Modelling, simulation and optimization of a packaging and palletizing system,” Applied Mechanics and Materials 760, 205-211. DOI: 10.4028/www.scientific.net/AMM.760.205

Ratnasingam, J., Latib, H., Lee, Y., Lim, C., and Khoo, A. (2019). “Extent of automation and the readiness for industry 4.0 among Malaysian furniture manufacturers,” BioResources 14(3), 7095-7110.

Ratnasingam, J., Yi, L., Azim, A., Halis, R., Liat, L., Khoo, A., Daud, M., Senin, A., Latib, H., Bueno, M., Zbiec, M., Garrido, J., Ortega, J., Gomez, M., Hashim, R., Zakaria, S., Abidin, S., and Amin, M. (2020). “Assessing the awareness and readiness of the Malaysian furniture industry for industry 4.0,” BioResources 15(3), 4866-4885.

Ray, Y., Zhong, X., Eberhard, K., and Stephen, T. (2017). “Newman. intelligent manufacturing in the context of industry 4.0: A review,” Engineering 3(5), 147-156. DOI: 10.1016/J.ENG.2017.05.015

Sembiring, M. T., and Kusumawaty, D. (2018). “Determination of service standard time for liquid waste parameter in certification institution,” in: IOP Conference Series: Materials Science and Engineering, 309(1), 012063. DOI: 10.1088/1757-899X/309/1/012063

Vijay, K. M., Kiran, K. B. J., and Rudresha, N. (2018). “Optimization of machining parameters in CNC turning of stainless steel (EN19) by TAGUCHI’s orthogonal array experiments,” Materials Today: Proceedings 5 (No. 5 Part 2). DOI: 11395-11407.10.1016/j.matpr.2018.02.107

Wang, J.-P. (2019). Research and Application of Furniture Board Packaging Algorithm, Master’s Thesis, Guangdong University of Technology, Guangdong, China.

Xiong, X.-Q., Ma, Q.-R., Yuan, Y.-Y., Wu, Z.-H., and Zhang, M. (2020). “Current situation and key manufacturing considerations of green furniture in China: A review,” Journal of Cleaner Production, 267. DOI: 10.1016/j.jclepro.2020.121957

Yang, W.-L. (2016). “Optimal and heuristic algorithms for constructing interference-free multicast trees subject to delay and energy constraints on wireless mesh networks,” International Journal of Ad Hoc and Ubiquitous Computing 22(2), 106-119.

Yang, X., and Jiang, Q. (2013). “Eliminating the information isolated island of EG system–A case study of CIQ,” Information Technology Applications in Industry, 2708-2711. DOI: 10.4028/www.scientific.net/AMM.263-266.2708

Zhang, H.-Y. (2011). “Rational consideration on package design of wooden furniture,” Advan. Mater. Res. 250-253. DOI: 10.4028/www.scientific.net/AMR.211-212.250

Article submitted: September 1, 2020; Peer review completed: November 17, 2020; Revised version received: December 3, 2020; Accepted: December 4, 2020; Published: December 21, 2020.

DOI: 10.15376/biores.16.1.1186-1206