Abstract
The flow characteristics of dilute aqueous suspensions of cellulose nanocrystals (CNC), nanofibrillated cellulose (NFC), and related products in dilute aqueous suspensions could be of great importance for many emerging applications. This review article considers publications dealing with the rheology of nanocellulose aqueous suspensions in the absence of matrix materials. In other words, the focus is on systems in which the cellulosic particles themselves – dependent on their morphology and the interactive forces between them – largely govern the observed rheological effects. Substantial progress in understanding rheological phenomena is evident in the large volume of recent publications dealing with such issues including the effects of flow history, stratification of solid and fluid layers during testing, entanglement of nanocellulose particles, and the variation of inter-particle forces by changing the pH or salt concentrations, among other factors. Better quantification of particle shape and particle-to-particle interactions may provide advances in future understanding. Despite the very complex morphology of highly fibrillated cellulosic nanomaterials, progress is being made in understanding their rheology, which supports their usage in applications such as coating, thickening, and 3D printing.
Download PDF
Full Article
Rheology of Nanocellulose-rich Aqueous Suspensions: A Review
Martin A. Hubbe,a Pegah Tayeb,a Michael Joyce,a Preeti Tyagi,a Margaret Kehoe,a,b Katarina Dimic-Misic,c and Lokendra Pal a
The flow characteristics of dilute aqueous suspensions of cellulose nanocrystals (CNC), nanofibrillated cellulose (NFC), and related products in dilute aqueous suspensions could be of great importance for many emerging applications. This review article considers publications dealing with the rheology of nanocellulose aqueous suspensions in the absence of matrix materials. In other words, the focus is on systems in which the cellulosic particles themselves – dependent on their morphology and the interactive forces between them – largely govern the observed rheological effects. Substantial progress in understanding rheological phenomena is evident in the large volume of recent publications dealing with such issues including the effects of flow history, stratification of solid and fluid layers during testing, entanglement of nanocellulose particles, and the variation of inter-particle forces by changing the pH or salt concentrations, among other factors. Better quantification of particle shape and particle-to-particle interactions may provide advances in future understanding. Despite the very complex morphology of highly fibrillated cellulosic nanomaterials, progress is being made in understanding their rheology, which supports their usage in applications such as coating, thickening, and 3D printing.
DOI: 10.15376/biores.12.4.Hubbe
Keywords: Nanocellulose hydrogels; Suspension viscosity; Nanofibrillated cellulose; Cellulose nanocrystals; Bacterial cellulose; Colloidal forces
Contact information: a: Department of Forest Biomaterials, North Carolina State University, Raleigh, NC 27695-8005; b: SNP Inc., 1301 South Briggs Ave., Durham NC 27703; c: School of Chemical Technology, Department of Forest Products Technology, Aalto University, 00076 Aalto, Helsinki, Finland;
* Corresponding author: hubbe@ncsu.edu
Contents
INTRODUCTION
Aqueous suspensions in which the viscous aspects are dominated by extremely small cellulosic materials have attracted increasing interest. A rising pace of related publications provides motivation for the present review article. Emphasis in this article will be placed on systems in which the presence of nanocellulose – which generally includes cellulose nanocrystals (CNC), nanofibrillated cellulose (NFC), and processed bacterial cellulose (BC) – have significant effects on flow phenomena (Nechyporchuk et al. 2016). As shown in Fig. 1, a search of the literature showed an accelerating rate of published articles considering related aspects over the last 25 years.
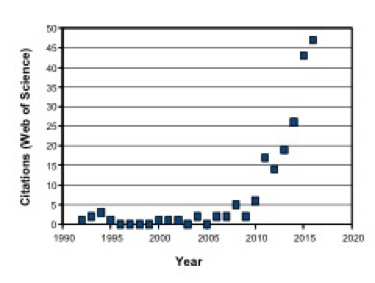
Fig. 1. Annual citations for publications dealing with the rheology of aqueous suspensions of nanocellulose [Search terms: Rheology; Cellulose*; (Nano* or Microfibril* or Crystal* or Whisker*), and then items wrongly present in the list (about half of them) were removed one by one.]
In the course of searching the literature, it became evident that articles dealing with the effects of nanocellulose on viscoelastic properties of solutions or materials fall into different classes, though the boundaries between such classes are often indistinct. A key point of differentiation is whether or not the viscoelastic effects are dominated by the nanocellulose (as in the present article) or by a polymer matrix, which may be a solution, a molten phase, or solid-like. Aspects of the latter type of system have been considered by others (e.g. Zimmermann et al. 2004; Khan et al. 2010; Moon et al. 2011; Ching et al. 2016). General aspects of the viscosity of suspensions of particles in viscous media have been considered by Mewis and Wagner (2012). Thus, the effects of adding nanocellulose to non-aqueous mixtures, melts, or already highly viscous phases of polymer will only be briefly considered in the present work, mainly for the sake of pointing out some contrasting behaviors.
Factors that can affect the viscoelastic behavior of aqueous suspensions that contain nanocellulose will be the primary focus of this article. In general, rheology can be regarded as a relatively mature field of study, within which the properties of different compositions can be well understood and often predicted with confidence (Malkin 2017). However, the structures and detailed surface chemistry of nanocellulose specimens are often incompletely known or too complex to describe accurately by a model equation. Therefore, many questions remain regarding the application of rheological principles to these materials. Aspects that will be considered in this review include effects of nanocellulose morphology and interactive forces between the surfaces. It will be emphasized that the rheological attributes of suspensions tend to be governed by both equilibrium and non-equilibrium (history-dependent) effects. Thus, attention will be paid to studies in which the morphological and surface-chemical attributes of nanocellulose in suspension were systematically varied.
Consequences of the Rheology of Nanocellulose Suspensions
The rheological properties of nanocellulose aqueous suspensions can have important consequences during their preparation, processing, and combination with other materials. Rheological properties of suspensions, including the stability of those properties over time, can be of critical importance for various industrial unit operations, such as pumping, mixing, filtering, storage, application, and metering. As indicated in Fig. 2, for instance, the rheological properties are often profoundly affected by the hydrodynamic shear during flow and pumping, and such rheological changes can be expected to affect whatever manufacturing operations are envisioned. As noted recently by Lindström (2017), the pre-shearing of a nanocellulose suspension, leading to momentarily reduced viscosity, may be important for many potential applications.
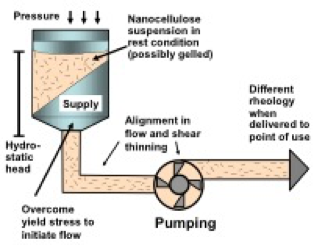
Fig. 2. Schematic representation of delivery system from a supply tank of nanocellulose suspension to its point of use, emphasizing some phenomena to be discussed in this article that tend to change the rheological behavior as a function of shearing and time
Stability with respect to temperature is important for ease of handling and to prevent process upsets when process interruptions occur. Stability of viscous behavior is also very important for maintaining good run conditions. Therefore, rheological measurements are frequently used to characterize nanocellulose characteristics, as well as for monitoring their behavior during their preparation and processing. The type of rheometer and accessories required for measuring rheological properties is dependent on various factors such as relevant shear rate, time scales, temperature, viscosity, sample size, etc. It has been documented that the use of serrated surfaces (in plate-plate rheometry) and a vane spindle (for bob in cup geometry) will decrease the wall-slip effects (Mohtaschemi et al. 2014a,b; Dimic-Misic et al. 2014; Nechyporchuc et al. 2015). Such issues are described in more detail later in this article. Table 1 lists publications in which various rheological measurements were recommended as a means of predicting likely outcomes of treatments for the preparation of nanocellulose suspensions. Figure 3 provides schematic views of some of the devices that have been employed in the reported analyses.
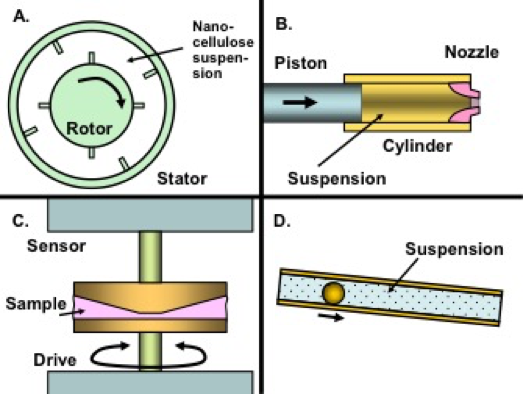
Fig. 3. Schematic views of some common ways to assess the viscosity of aqueous nanocellulose suspensions: A: Couette-type rheometer with baffles (related to “bucket and vane” devices) (Dimic-Misic et al. 2014); B: Extensional viscometer (Dimic-Misic et al. 2015a); C: Cone and plate rotational viscometer (Tanaka et al. 2014); D: Rolling ball viscometer (Tsvetkov et al. 2016)
Figure 4 illustrates alternative systems that utilize either serrated plates or vanes to enable rheological measurements while avoiding wall depletion effects.
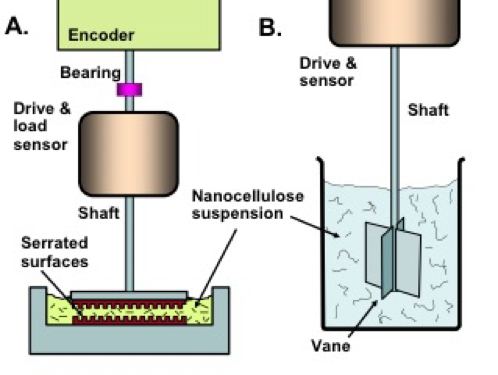
Fig. 4. Schematic views of (a) serrated plate system and (b) vane system for evaluation of suspension rheology while minimizing effects due to wall depletion
Table 1. Publications Suggesting Usage of Rheological Measurements as a Means of Characterizing Nanocellulose Attributes
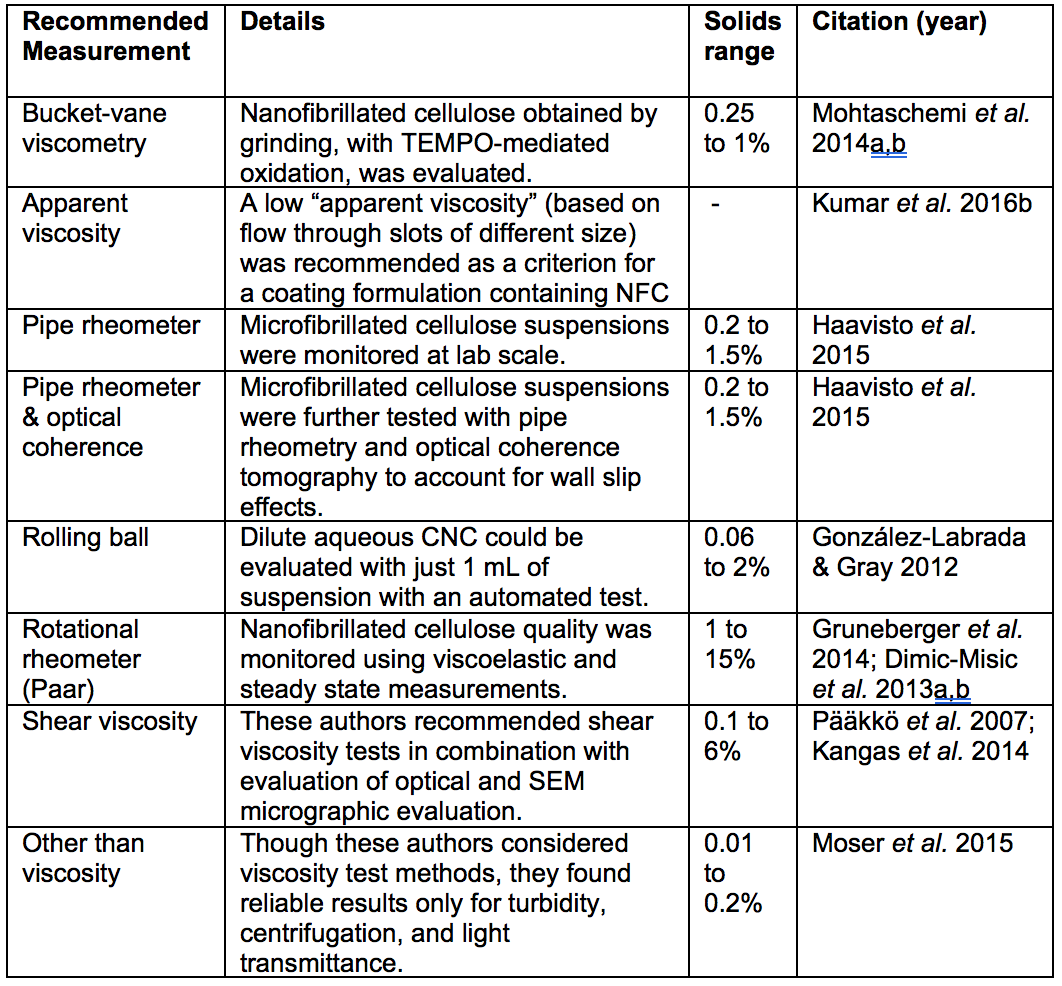
Some of the criteria that have been considered when selecting a test device (as will be noted in later sections) include avoiding slip effects at the wall boundaries, providing a wide enough “gap” in the device to accommodate the suspended solids (including any network structures), and being able to carry out tests with small amounts of suspension.
Applications Involving Rheology
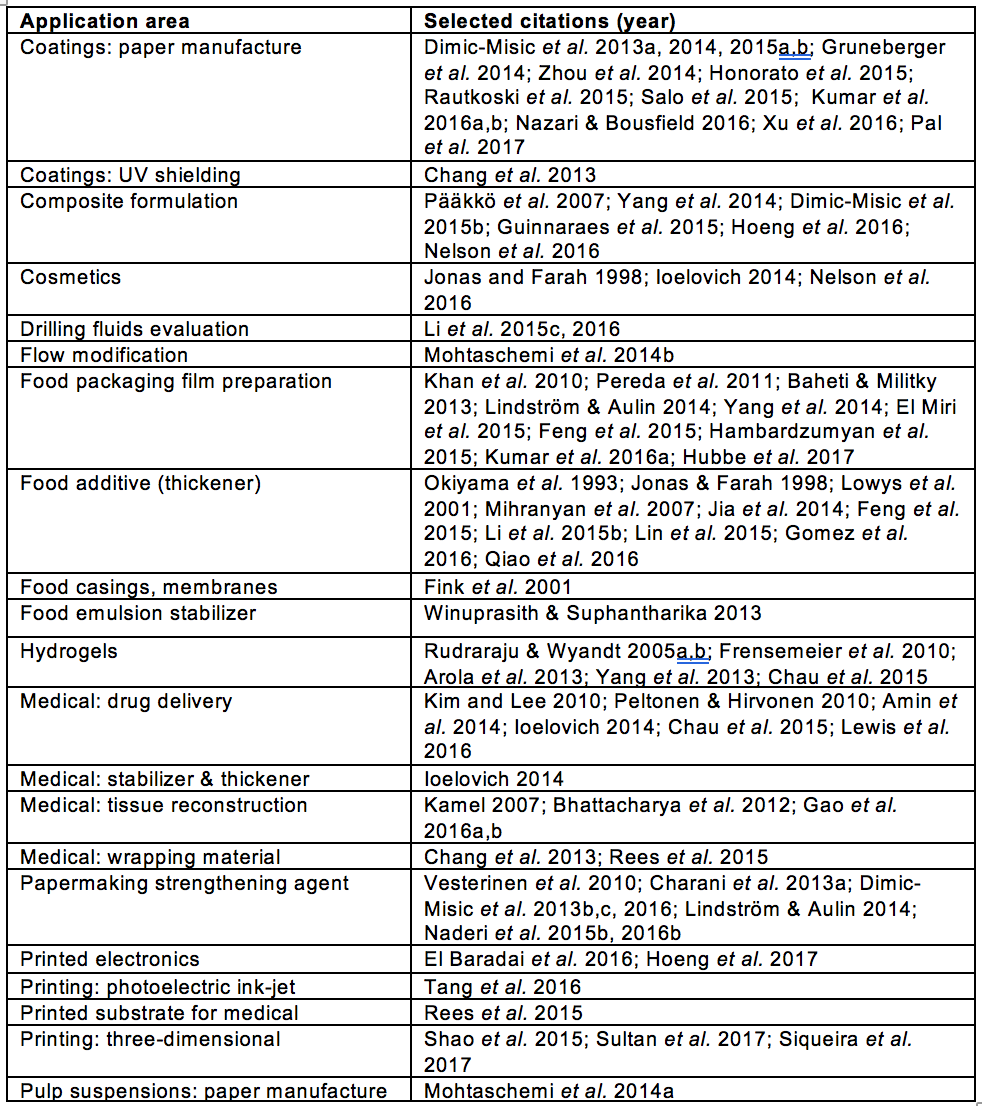
The rheological properties of nanocellulose suspensions can play a major role in different applications, such as thickening, coating, composites, and 3D printing. Table 2 lists various sources that discuss such potential or present uses of nanocellulose.
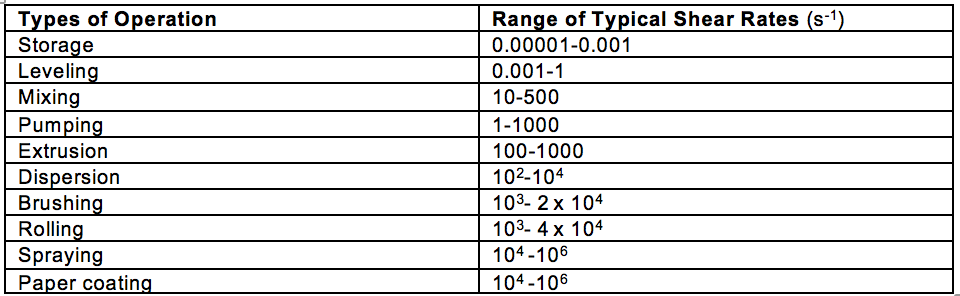
Regardless of the application, the rheological properties of any material is of high importance for the handling and use of a material during application and processing, which can occur over a broad range of shear rates. Table 3 shows generally accepted ranges of shear a material might experience during application and use.
Table 2. References Noting Various Applications in which the Rheology of Nanocellulose Aqueous Suspensions Are Important
Some factors that can strongly influence the rheology of a suspension are the number of particles present and the volume fraction they occupy. A high solids fraction is often desired to reduce material transport and processing costs. Efforts to increase the solids level can benefit from an understanding of the effects of nanocellulose morphology and interactive forces between the nanocellulose surfaces. This is best accomplished by studying the flow characteristics of dilute aqueous suspensions. Other factors of importance are particle size, size distribution, shape, and interactions between particles. The interactions will be discussed in the section dealing with surface chemistry effects.
Table 3. Typical Ranges of Shear Rate for Common Industrial Operations (s-1)
General Effects of Flow
As background for later discussion of the rheological effects of nanocellulose in suspensions, selected general references can be recommended. Basic aspects of hydrodynamics, including a discussion of patterns of flow likely to be encountered in industrial applications, can be found in the book by Malkin (2017). The subject of extensional viscosity and related flow phenomena also have been elucidated, though to a limited extent (Petrie 2006). Time-dependent viscoelastic effects, including thixotropy, have been covered in well-known texts (Barnes 1997; Mewis and Wagner 2009, 2012; Puisto et al. 2012b). In addition, much is known about the rheology of suspensions of non-spherical particles (Chinesta and Ausias 2016). Aspects of the rheology and the viscosity of fluids containing nanoparticles also has been reviewed (Wierenga and Phillipse 1998; Mahbubul et al. 2012). Solomon and Spicer (2010) considered the rheological aspects of suspensions of rod-like particles, focusing on effects of aspect ratio and solids content for a wide range of natural and synthetic rod-like materials. They emphasized differences between gels (having a heterogeneous fractal-like structure) and glasses (having homogeneous network structure). Particular attention will be paid here to some non-reversible effects of stresses, strains, and time on the subsequent viscoelastic behavior of suspensions.
NANOCELLULOSE CHARACTERISTICS RELEVANT TO RHEOLOGY
Factors to Be Considered
Factors affecting the rheological properties of nanocellulose-containing aqueous suspensions can be regarded as falling into two useful categories. One of the most important is morphology, i.e. size and shape of fibrils. Another main point of differentiation is the surface-chemical composition of the solids, which can affect the surface charge. Both the morphology and surface composition can depend on the processes of treatments used to prepare the material. Therefore, a summary of nanocellulose preparation will be given in subsections that follow, with an emphasis on morphology and surface composition. For the sake of completeness, some key findings related to the influence of the viscosity of the suspending medium, in the case of nanocellulose suspensions, also will be reviewed.
Some of the morphological aspects that have received much attention, relative to suspension rheology, can be encompassed by the terms fiber length, fiber diameter, fibrillation, and network structure. Table A (see Appendix) includes such information from the articles considered in this review. Likewise, aspects of surface chemistry of the nanocellulose can often be summarized by terms such as electrostatic or ionic charge, and hydrophilic or hydrophobic nature. In addition, the tendencies of cellulosic materials to swell in water can involve both morphology and surface chemistry.
The most important classes of nanocellulose, in terms of the volume of recent research publications, can be differentiated primarily by their processing, and secondarily by their biological origin. Research related to cellulose nanocrystals (CNCs) will be considered first, since CNCs tend to be the smallest and simplest of the nanocellulose entities, containing only crystalline domains of cellulose polymer. The main means of their isolation from the starting macroscopic cellulosic material is chemical digestion – most often with concentrated acid solution (Eichhorn 2011; Mariano et al. 2014). Alternatively, they can be prepared by oxidization, using ammonium persulfate (Leung et al. 2011) or the 2,2,6,6-tetramethylpiperidine-1-oxyl radical (TEMPO) (Hirota et al. 2010).
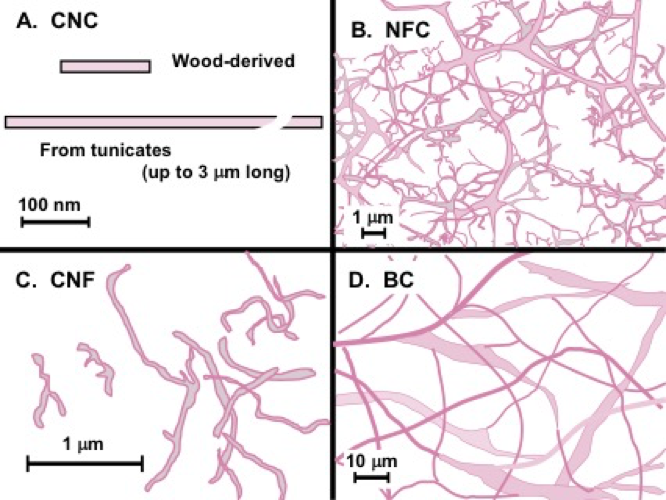
Fig. 5. Simplified diagrams to contrast the typical filament widths and shapes of nanocellulose materials that have been considered in various studies of rheological properties. Graphics were patterned after the following sources: A – multiple sources (cellulose nanocrystals); B: Crawford et al. 2012 (nanofibrillated cellulose); C: Iwamoto et al. 2014 (cellulose nanofibrils); D: Shi et al. 2012 (bacterial cellulose)
By contrast, mechanical processing, often accompanied by chemical or enzymatic pretreatment, plays a dominant role in the preparation of highly fibrillated cellulose materials (Siro and Plackett 2010; Lavoine et al. 2012; Sandquist 2013). In this article such materials will be referred to generally as either nanofibrillated cellulose (NFC) or microfibrillated cellulose (MFC) (Klemm et al. 2011). These labels can be regarded as synonyms, except that the term “nano” is used by many authors to emphasize a smaller size range. The term cellulose nanofibrils (CNF) (Nechyporchuk et al. 2016), which is also sometimes called “cellulose nanofibers,” will be used in this article in a narrow sense, referring to suspensions in which most of the fibrils mostly have been completely detached from each other, so there are no branched or network structures present. Exceptions include possible entanglements or agglomeration that is brought about by attractive forces.
Both CNCs and the fibrillated cellulose can be obtained from a wide variety of plant sources, including bacterial cellulose (BC). However, BC has a special status, since some varieties of BC are already in a similar “nano” size range as NFC even when they are first isolated (Moon et al. 2011). Figure 5 provides a simplified pictorial view of the main form of nanocellulose to be considered in this article.
Cellulose Nano-crystals (CNCs)
Preparation
As described in review articles, CNCs are most commonly prepared by digestion of cellulose in concentrated sulfuric acid (Araki et al. 1998; Gu et al. 2013; Mascheroni et al. 2016), hydrochloric acid (Gu et al. 2013), or other acids (Naderi et al. 2016b), sometimes with the addition of enzymes (Chen et al. 2012; Anderson et al. 2014). As illustrated in Fig. 6, the procedure can be understood based on an envisioned nanostructure of cellulose, in which crystalline regions are interposed by short non-crystalline or damaged regions (Nishiyama et al. 2003). Hirota et al. (2010) showed that CNC also can be prepared by relatively severe TEMPO-mediated oxidation of regenerated cellulose. Efforts are under way to produce CNC profitably at an industrial scale (Moser et al. 2015; Nelson et al. 2016). Some typical treatment conditions are 65% H2SO4 at 70 °C with stirring for 20 minutes (Araki et al. 1998). The main idea is to cleave and dissolve non-crystalline parts of the cellulose and any remaining hemicellulose, leaving behind just the nanocrystalline elements that are presumed to have been present in the starting material. Common plant sources for production of CNCs include delignified wood, cotton, bacterial cellulose, and even regenerated cellulose (Eichhorn 2011; Mariano et al. 2014).
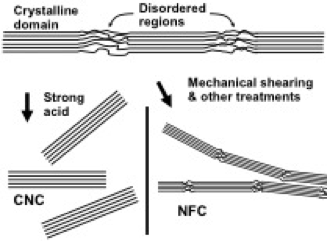
Fig. 6. Schematic illustration of preparation of two contrasting types of nanocellulose, starting with native cellulosic material. Digestion of amorphous regions leads to cellulose nanocrystals (CNCs), whereas mechanical fibrillation (often with the assistance of chemical treatments) can yield nanofibrillated cellulose.
Typical dimensions
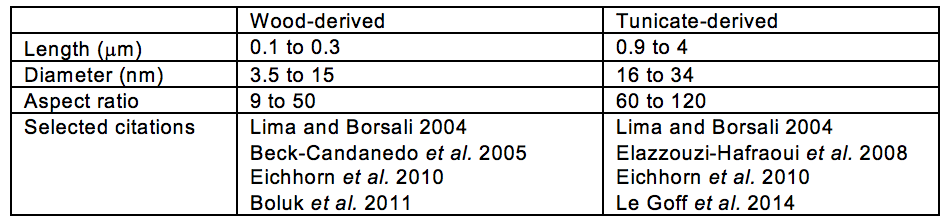
Table 4 lists typical dimensions of CNCs, based on the data collected in Table A (see Appendix). Though the dimensions shown can be regarded as typical, a wide range of dimensions is possible, given the many kinds of source materials and the many isolation strategies that have been employed. While the term “diameter” is shown in the table for this general description, it is worth noting that the cross-section of CNC in generally regarded as either rectangular (Eichhorn 2011) or hexagonal. In particular, an 18-chain hexagonal model has been proposed (Cosgrove 2014).
Table 4. Representative Characteristics of Cellulose Nanocrystal (CNC) Batches
Factors affecting crystal length
One can find different explanations in the literature to account for both the length and the thickness of CNCs. For instance, it has been proposed that the sizes of the crystals obtained after acid digestion are a close reflection of the dimensions of crystalline domains originally present in the cellulosic source material (Araki 2013). Regarding the length, it has been proposed that the native cellulose within lignified plants (e.g. including wood) have quite regular patterns of periodic defects or interruptions in their crystal structure (Araki 2013). Nishiyama et al. (2003) proposed that short polymer chain segments, maybe having approximately five anhydroglucose units, show deviations from the crystalline organization within an elementary fibril. Based on these findings it can be hypothesized that such defects would arise naturally during repeated flexing of a woody plant during its growth, exposure to wind, cycles of moisture change, or effects of thermal stresses (Takahashi et al. 2006; Lucander et al. 2009; Tomczak et al. 2012). As evidence to support the concept that mechanical stresses can cause damage at a molecular level, Joutsimo and Giacomozzi (2015) reported that mechanical stresses encountered by fibers during ordinary industrial processing of kraft fibers affects the fiber nanostructure and can affect the resulting paper properties significantly; fibers prepared to the same specifications under the mechanically gentler conditions of laboratory evaluation exhibited higher strength properties. Another likely explanation is that defects in the cellulose crystal structure are induced by the presence of other cell wall polysaccharides (Cosgrove 2014). Kontturi and Vuorinen (2009) found that CNC particles prepared from never-dried chemical pulps tended to be longer than those prepared from the corresponding dried pulps; it follows that the stresses imposed on the material during drying can induce periodic damage to the crystalline domains.
Some of the longest CNCs, with lengths ranging up to about 4000 nm, have been reported in the case of animal-derived cellulose, as obtained from the protective spines of tunicates (Lima and Borsali 2004; Elazzouzi-Hafraoui et al. 2008; Eichhorn et al. 2010). Unlike typical plant-derived CNCs, the “whiskers” obtained from tunicates generally show very wide distributions of length (Elazzouzi-Hafraoui et al. 2008). This can be tentatively attributed to the relatively infrequent and irregular occurrence of damaging levels of stress on the material during an ordinary life cycle of the animal.
Hairy CNCs
While CNCs are ordinarily regarded as having a simple shape, as would be expected for a crystal, recent work by Lenfant et al. (2015) and van de Ven and Sheikhi (2016) presented CNCs having protruding macromolecular cellulose chains from the ends of the crystals. This is illustrated schematically in Fig. 7. Instead of using concentrated acid, the cited study employed a solution of meta-periodate, an oxidizing agent. Fibrils at the ends of the crystals were substantiated by transmission electron microscopy. Colloidal stability, which was enhanced at neutral to moderately high pH, was ascribed to the carboxylic acid groups provided by periodate oxidation of the protruding chains. Since protruding chains appear not to have been reported for CNCs produced by hydrolysis with acids or cellulases, it seems likely that these features can be expected only in the absence of cellulose-hydrolyzing agents.
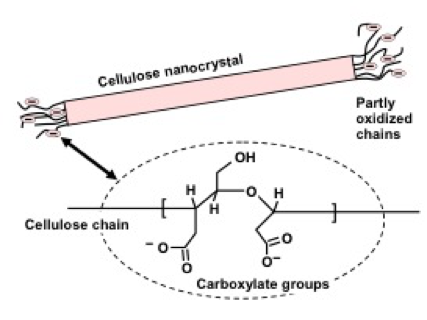
Fig. 7. Schematic view of CNC prepared by periodate oxidation, in which oxidized cellulose chains extend from the ends of the crystals
Highly Fibrillated Cellulose Products
The application of very extensive mechanical shearing of cellulosic materials gives rise to a class of highly fibrillated materials, which generally contain both crystalline and amorphous cellulose. The names microfibrillated cellulose (MFC) and nanofibrillated cellulose (NFC) roughly correspond to different size ranges; however, the demarcation between MFC and NFC can be difficult to distinguish (Kangas et al. 2014). The term cellulose nanofibrils (CNF), which would literally mean that the fibrils are completely detached from each other, has become popular when referring to highly fibrillated cellulose preparations (Eichhorn et al. 2010); however, the term appears to be often misapplied to highly branched or network-like structures rather than suspensions of individual fibrils.
As a working definition, in the present article the term NFC can be taken to mean that the lengths have been substantially (e.g. at least 10 times) reduced compared to the fiber source and the widths or diameters of most of the cellulosic elements are no more than about 100 nm. Interestingly, the definition just stated (intended to define NFC) is substantially broader than the early definition for cellulose microfibrils given by Chanzy (1990), i.e. up to tens of mm in length and 2 to 20 nm in diameter. At the high end, various authors have used the term MFC to designate cellulosic fibers that were nearly their original size, but which had high levels of fibrillation (Haavisto et al. 2015; Moser et al. 2015; Zhang et al. 2015; Schenker et al. 2016; Shafiei-Sabet et al. 2016). Efforts to bring some order to the classification have been attempted (Kangas et al. 2014). The rheological aspects of this kind of cellulose have been recently reviewed (Iotti et al. 2011; Naderi and Lindström 2015; Nechyporchuk et al. (2016).
Faced with the difficulty of directly measuring the aspect ratio of NFC samples, with their branched and network-like attributes, Varanasi et al. (2013) based their estimates on the solids level in aqueous suspension corresponding to detection of gelation (see later discussion).
Fibrillation means
Details of the behavior of highly fibrillated cellulose products can be expected to depend on the type of mechanical action used for size reduction. Several different types of equipment are in current use to prepare highly fibrillated cellulose at various scales of production. In general terms, it appears that similar results can be achieved using contrasting equipment.
Conventional refining equipment, as used for many years in paper manufacture, can be employed, sometimes using modified refiner plates, to produce highly fibrillated celluloses (Kamel 2007; Chen et al. 2016a; Shafiei-Sabet et al. 2016). An advantage of such an approach is that industrial-scale equipment already exists and can be regarded as mature technology. On the other hand, there is no assurance that such equipment has an optimal format when the goal is not to prepare the fibers for ordinary papermaking, but to greatly reduce the dimensions of the cellulosic material.
High-pressure homogenizers have been used in several reported studies of the rheology of nanocellulose suspensions (Gouse et al. 2004, Kamel et al. 2007; Pääkkö et al. 2007; Besbes et al. 2011a,b; Hassan et al. 2011; Liu et al. 2011; Shogren et al. 2011; Li et al. 2012; Zhang et al. 2012; Osong et al. 2013; Winuprasith and Suphantharika 2013; Benhamou et al. 2014; Grueneberger et al. 2014; Kekalainen et al. 2014a; Lindström and Aulin 2014; Naderi et al. 2014a; Chaker and Boufi 2015; Lin et al. 2015; Naderi et al. 2015a,b; Beaumont et al. 2016; Chen et al. 2016b; Hellström et al. 2016; Hiasa et al. 2016; Pääkkönen et al. 2016). These devices work by forcing a suspension through a narrow space with abrupt changes in direction. Key variables are the operating pressure and the number of passes. Kekalainen et al. (2014a,b; 2015) achieved related effects using an inline homogenizer, where the suspension passed between a rotor and stator with a gap of less than 1 mm between alternating sets of teeth projecting into the high-shear zone.
Naderi et al. (2015c) considered a strategy to potentially reduce the energy and improve the outcomes of treatment in a homogenizer. Repeated passes were evaluated as a potential advantageous option in comparison to higher pressure processing with a single pass. Interestingly, these authors observed that films prepared from the highly fibrillated cellulose reached their ultimate strength when using only 40% of the energy required to fully reduce the material to NFC.
Microfluidizers, which involve the collision of opposing streams of suspensions, have also been used to prepare highly fibrillated nanocellulose (Charani et al. 2013a,b; Rezayati Charani et al. 2013; Naderi et al. 2015c, 2016b; Dimic-Misic et al. 2016; Samyn and Taheri 2016; Taheri and Samyn 2016). A possible advantage of this approach is reduced wear on the equipment.
Microgrinders are widely used to produce highly fibrillated cellulose, especially under laboratory conditions (Hassan et al. 2011; Mohtaschemi et al. 2014a; Bettaieb et al. 2015). The microgrinding procedure consists of passing a cellulose suspension between pairs of rough ceramic surfaces, usually prepared from high-hardness SiC mineral particles (Mohtaschemi et al. 2014a).
Chemical assistance to fibrillation
The amount of energy required to produce highly fibrillated cellulose products constitutes a major area of concern, especially for those considering the costs of scaling up processes for commercial production (Zimmermann et al. 2010; Lindström and Aulin 2014; Moser et al. 2015; Naderi et al. 2016a; Nelson et al. 2016). Various treatments with chemicals or enzymes are under investigation to reduce the energy required.
Treatment of cellulose with the relatively stable free-radical species 2,2,6,6-tetramethylpiperidine-1-oxyl radical (TEMPO) in the presence of an oxidizing agent has become a popular route to the production of NFC under reduced energy requirements (Lasseuguette 2008; Lasseuguette et al. 2008; Johnson et al. 2009; Hirota et al. 2010; Besbes et al. 2011a,b; Ishii et al. 2011; Loranger et al. 2012a,b; Mishra et al. 2012; Araki 2013; Benhamou et al. 2014; Fukuzumi et al. 2014; Kekalainen et al. 2014a, 2015; Lindström and Aulin 2014; Mohtaschemi et al. 2014a,b; Nechyporchuk et al. 2014, 2015; Bettaieb et al. 2015; Jowkarderis et al. 2015; Martoia et al. 2015, 2016; Rees et al. 2015; Pääkkönen et al. 2016; Xu et al. 2016). In addition to facilitating the fibrillation of the material, TEMPO-mediated oxidation also imparts a negative charge to the surfaces (at pH values near to or above the pKa value of the carboxylic acids) (Hirota et al. 2010; Isogai et al. 2011; Fukuzumi et al. 2014; Isogai 2015). Because the TEMPO system tends to exclusively oxidize the C6-hydroxyl groups of cellulose, it causes only a moderate reduction of molecular mass (Isogai et al. 2011). It has been estimated that TEMPO-mediated oxidation can enable a reduction of energy by a factor of between 24% and 54% when achieving an approximately equivalent level of fibrillation of the cellulose (Delgado-Aguilar et al. 2015).
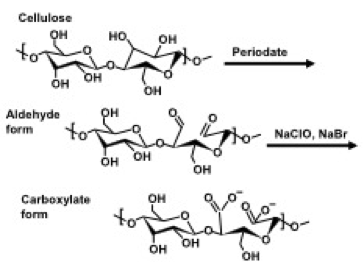
Fig. 8. Reaction sequence for conversion of cellulose to the corresponding aldehyde and carboxylate forms
Other means of establishing carboxylic acid groups at cellulosic surfaces can be used. As indicated in Fig. 8, periodate oxidation, which favors conversion of the C2 and C3 hydroxyl groups to aldehydes and carboxylic acids, also has been evaluated for enabling the easier production of highly fibrillated celluloses (Kekalainen 2014b). Rees et al. (2015) evaluated a combined treatment with TEMPO and periodate. Naderi et al. (2014a,b, 2015a,c, 2016a) achieved energy reductions by carboxymethylation of the cellulose before application of high shear to prepare NFC. Again, the effect of increasing the carboxylic acid content at the cellulose surface was to reduce the energy needed to make NFC. Naderi et al. (2016b) achieved related effects with phosphorylation as a pretreatment before nanofibrillation. The fore-mentioned strategies, based on imparting a negative charge to cellulose, appear to facilitate easier fibrillation and help to electrostatically stabilize the suspensions (see later).
Another promising strategy for energy reduction consists of the partial degradation of the non-crystalline parts of the cellulose chains by optimized cellulase enzymatic treatment (Pääkkö et al. 2007; Hassan et al. 2011; Hellström et al. 2014, 2016; Martoia et al. 2015; Naderi et al. 2015b; Beaumont et al. 2016; Dimic-Misic et al. 2016; Naderi and Lindström 2016; Naderi et al. 2016a). Beaumont et al. (2016) were able to achieve in one pass of high-pressure homogenation of enzymatically hydrolyzed cellulose what needed up to about 20 passes in the absence of such treatment. Nechyporchuk et al. (2014) used a combination of cellulase and TEMPO mediated oxidation to promote the fibrillation of NFC.
Moderately hydrophobic modification of NFC was reported by Missoum et al. (2012a), who grafted long aliphatic chains onto the cellulose. Notably, despite an appreciable level of substitution, the modified NFC was still dispersible in water. The cited authors attributed this water-compatibility to a combination of self-association of hydrophobic groups and the persistence of uncovered, hydrophilic areas on the NFC surfaces.
Network vs. separated structure of fibrillated celluloses
Micrographs of NFC products most often show highly complex structures that would be better described as networks rather than individual fibrils (Chen et al. 2016b; Martiola et al. 2016; Naderi et al. 2016b). For instance, Shogren et al. (2011) described corn cob tissue subjected to two passes of blender action as “networks of microfibrils and larger expanded fibrillar aggregates, while bundles of more separate microfibrils were observed after eight passes”. Chen et al. (2016b) report a “highly tangled fibril network”. Naderi et al. (2014a) use the term “severely entangled structure”. The high aspect ratio and charged nature of nanofibrillated cellulose gives rise to water-trapping properties. The NFC characteristics trigger a mechanism that constructs a gel and can lead to structure ensemble orientation. Strong electrostatic repellence of the highly charged nanoparticle surfaces and the “immobilization of the trapped interstitial water enable creation of elastic structured zones of fibrillated agglomerates within gel matrix” (Dimic-Misic et al. 2016).
Only in exceptional cases have individualized fibrils been reported as being derived from mechanical shearing – usually when accompanied by enzymatic treatment or intensive chemical oxidation (Pääkkö et al. 2007; Iwamoto et al. 2014; Jowkarderis and van deVen 2014; Kekalainen et al. 2015; Li et al. 2015a). Based on reported images, typical lengths of the aggregated structures are often in the range of 20 to 1000 mm. The widths are often in the range 20 to 500 nm. Thus, although the fibrils that compose typical NFC can be clearly in the “nano” range, the gross structure is typically a lot larger. The fact that such structures are firmly joined together by cellulosic elements needs to be kept in mind when considering efforts to predict rheological behavior based on measured or estimated dimensions.
Products that are relatively free of branch points and mechanically joined networks will be referred to in this article as cellulose nanofibrils (CNFs). It is notable that the combination of very high aspect ratio, the presence of both amorphous and crystalline cellulose, and the lack of branching or networking is shared by some forms of bacterial cellulose (native or processed), which will be considered next.
Bacterial Cellulose (BC)
Morphological aspects and other details about bacterial cellulose have been reviewed by Jonas and Farah (1998) and by Moon et al. (2011). Based on the number of publications, there has been strong interest in bacterial nanocellulose due its fibrils’ extremely high elastic moduli (78 GPa), high crystallinity, and absence of hemicellulose. These attributes enable a wide range of possible utilizations in films and aerogels. Bacterial cellulose nanofibrils (BC), such as the Acetobacter species (Iguchi et al. 2000; Lee and Bismarck 2012), have an advantage of being free from wax, lignin, hemicellulose, and pectin, which are all present in plant-based cellulosic materials (Pommet et al. 2008; Lee and Bismarck 2012). Surface modification of natural fibers with bacteria has been employed to deposit bacterial cellulose onto natural fibers to create hierarchical fiber reinforced nanocomposites (Pommet et al. 2008). When high aspect ratio bacterial cellulose is well disintegrated, its rheological behaviour can resemble that of liquid crystals (see later discussion). This suggests that BC fibrils in suspension, under certain shearing conditions, can become oriented, showing “order-disorder” alignment. Such properties of suspensions can be in turn utilized to make anisotropic films or aerogels. The crystallinity index (Cr. I) values of BC films were found to be around 78%) (Tsalagkas et al. 2015). However, it is difficult to define with precision the dimensions of single BC fibrils, as upon fluidization, a suspension may still contain fibrils that are mechanically bonded as part of larger fibril structures (Pääkkönen et al. 2016).
Table 5 lists relevant publications and their main findings with respect to fibrillar dimensions.
Table 5. Reported Bacterial Cellulose Dimensions and Descriptions

As a general rule, native bacterial cellulose consists of very high aspect-ratio fibrils. The length of bacterial cellulose fibrils is seldom reported, and published images often fail to show ends of fibrils (Feng et al. 2015; Pääkönen et al. 2016). Mechanical processing appears especially effective in separating the material laterally into thinner fibrils, while preserving a long length (Lin et al. 2015; Paximada et al. 2016). Thus, the format that one sees in micrographs is often a tangled loose coil or coils (Paximada et al. 2016). Okiyama et al. (1993) and Pääkönen et al. (2016) used the term “flocs” to describe BC suspensions. Authors have reported relatively high levels of water retention, i.e. swelling of bacterial cellulose, e.g. 2 to 4 g/g, relative to other highly fibrillated nanocellulose (Amin et al. 2014). These values are comparable to the water retention of xylan-free NFC suspensions (Pääkonen et al. 2016). The latter authors estimated an agglomerate diameter equal to 5 mm.
Contributions from the Viscosity of the Aqueous Medium
Though nanocellulose is assumed, in this article, to make the major contribution to rheological effects, the viscosity of the suspending medium cannot be ignored, so some points merit review. General background regarding viscous effects in particle-free aqueous systems can be found in available texts (Larson 2005; Malkin 2017). Some factors that can affect the rheology of the medium, and consequently the rheology of the nanocellulose suspension, are discussed in the subsections that follow. Issues related to ionic strength and pH will be deferred to a later section, which focusses on colloidal chemistry effects.
Temperature
In ordinary aqueous media, increasing temperature tends to decrease the coefficient of viscosity in a smooth, predictable way. The viscosity of pure water decreases markedly as the temperature is raised (Korson et al. 1969). That generally implies that water’s contribution to the viscosity of a suspension will decrease with increasing temperature. However, Agoda-Tandjawa et al. (2010) observed no additional important effect of temperature on the viscosity of a NFC suspension. Such findings are consistent with a dominant effect of the nanocellulose on the measured viscosity, noting that the temperature also can affect such factors as the degree of dispersion of the solids and the flexibility of the fibrils.
Polyelectrolytes in solution
When considering viscosities of aqueous mixtures, the effects of polyelectrolytes need to be considered. Dissolved polyelectrolytes, when present in aqueous mixtures with nanocellulose, may remain in the water phase either when they have a low adsorption affinity or when the amount exceeds the adsorption capacity of the surfaces. The emphasis in this review is on system in which polyelectrolytes, if present, are not so concentrated as to dominate viscous effects, relative to the effects of the nanocellulose. The incremental effects of such dissolved polyelectrolytes on the solution viscosity can be estimated from the concentration, molecular mass, and the tendency of the polymer to adopt an expanded conformation (Larson 2005; Malkin 2017). In principle, the viscosity characteristics of polyelectrolytes solutions serving as the suspending medium for solids particles, will be related to the observed viscosities of suspensions, but in a complex way, due to particle-solution interactions.
Even when water-soluble polymers are to be present in the final mixture, it sometimes can be advantageous to initially disperse nanocellulose in their absence. Thus, Going et al. (2015) studied the dispersion of CNC into poly(vinylpyrrolidone, PVP). They dispersed CNC into water prior to the subsequent addition of methanol as a co-solvent in the polymer matrix, which reduced the viscoelasticity properties of the solution. They attributed this reduction to less agglomeration of the nanocellulose.
In the work by Butchosa and Zhou (2014), CMC was adsorbed on the colloidal NFC, and its effect on the system viscosity was monitored. They reported, at the level of 2.3 wt% CMC, that a fully redispersible NFC was achieved. A pertinent example is viscosity reduction of NFC solution as a result of xyloglucan adsorption, which was studied by Ahola et al. (2008)
Unusual viscosity behavior of CNCs dispersion in polyoxyethylene (PEO) solution was reported by Ben Azouz et al. (2012). With increasing addition of CNC, up to 9 wt.%, the viscosity continued to decrease; however, this trend became reversed at higher levels. These observations are in agreement with Cox-Merz rule that will be discussed later in this article.
Bridging effects of nanocellulose
At the limit of relatively low additions of nanocellulose to solutions of polymers in water, the cellulose nanofibrillar aggregates suspended in a gel-like matrix can sometimes function as a kind of cross-linking agent, linking some of the polymers to each other and building the viscosity. For instance, Yang et al. (2014) studied addition of CNC to polyethylene glycol solutions. Strong enhancements in viscosity were observed. Rheological behavior of a 1.0% water solution of hydroxyethyl cellulose mixed with carboxymethyl cellulose (CMC) was studied by Boluk et al. (2012). They observed a significant increase in the viscoelasticity and formation of a gel-like solution, upon addition of cellulose nanocrystal (CNC) into the system. Related effects have been widely reported (e.g. by Guo and Ding 2006; Vesterinen et al. 2010; Boluk et al. 2012; Hu et al. 2014; Lu et al. 2014c; Ahn and Song 2016; Oguzlu et al. 2016).
At ranges of polymer concentration sufficient to dominate viscous effects, when adding nanocellulose, it may be more appropriate to refer to the mixture as a nanocomposite (Hubbe et al. 2008; Eichhorn et al. 2010; Moon et al. 2011; Hubbe et al. 2017) rather than as an aqueous suspension. The rheological properties of nanocellulose-reinforced polymer matrices have been reviewed elsewhere (Moon et al. 2011; Ching et al. 2016).
PHYSICAL ASPECTS OF SUSPENSION VISCOSITY
Rheology of Particle Suspensions
Factors that can affect the viscosity and viscoelasticity of suspensions of nanomaterials generally can be assigned to the categories “physical” and “chemical”. The physical aspects, which will be considered in this section, include sizes, shapes, mechanical properties of materials, flow, formation of flocs, certain yield-point issues, and “wall slip” effects, etc. Many of these physical aspects have general applicability to a broad range of mixtures, so it makes sense to consider them first. Details about the non-hydrodynamic forces of interaction between surfaces tend to be dominated by chemistry – and these will be considered in a later section.
Einstein’s theory
Einstein derived a fundamental relationship to predict the viscosity of Newtonian fluids that contain neutrally-buoyant, non-interacting spheres (Einstein 1911; Mueller et al. 2010). The presence of the spheres was predicted to increase the viscosity, relative to that of the pure liquid (ho), according to Mueller et al. (2010),
h = ho (1 + Bo f) (1)
where f is the volume fraction of the spheres (assumed to be of equal size). According to Einstein, the coefficient Bo should be 5/2, but others have assigned values between 1.5 and 5, based on other sets of assumptions. To be able to apply the equation beyond the highly dilute range, subsequent workers have derived higher-order terms. For instance, the viscosity can be expressed as,
h = ho (1 + 5/2 f + B1 f 2) (2)
where the coefficient B1 has been assigned values between 2.5 and 7.35 (Mueller et al. 2010), depending on whether one accounts for effects of Brownian motion and inertia. Alternatively, to extend the range of accuracy up to about 4% by volume, Brinkman (1952) proposed the following equation (Mahbubul et al. 2012):
h = ho (1 – f)2.5 (3)
Experimental data are often fitted to semi-empirical equations of the form (Krieger 1959; Chen et al. 2007; Mahbubul et al. 2012),
![]() (4)
(4)
where the relative viscosityhr is the ratio between the viscosity of the mixture and that of the suspending liquid, B is the Einstein coefficient, and fm is the maximum packing density volume fraction (equal to about 0.64 for equal spheres). Similar models have been employed for nanocellulose materials by considering them as elongated particles (Nechyporchuk et al. 2016). A relationship similar to Eq. 4 was derived by Dougherty (1959) and Krieger (1972), except that the exponent was –[h] . A yet simpler form, in which the exponent was given as -2, was reported by Maron and Pierce (1956) and Quemada (1982).
Several researchers have employed relationships such as that shown in Eq. 5 to report their results (see Table A). In other words, the measured viscosity can be reported to be dependent on the volume concentration raised to an empirically determined coefficient.
![]() (5)
(5)
As noted in the review by Klemm et al. (2011), the storage modulus of nanocellulose suspensions is often found to follow an analogous relationship,
![]() (6)
(6)
in which the exponent should be 2.25 according to scaling theory (de Gennes 1979). The exponent has been found to be about 3 for volume concentrations above 0.5% (Klemm et al. 2011).
Rheological behavior of nanocellulose suspensions is usually determined by fitting of experimental data of flow curves. The viscosity is commonly observed to decrease with increasing shearing as a power law according to the Oswald de-Waele empirical model; this relationship can be expressed as Eq. 7 (Lasseuguette et al. 2008; Divoux et al. 2013),
![]() (7)
(7)
where k and n are the flow index and the power-law exponent, respectively. The parameter g is the shear rate, usually expressed in s-1. An exponent value of zero indicates a Newtonian fluid, and n > 0 pseudo-plastic (shear thinning) behavior (Dimic-Misic et al. 2014).
Nanocellulose gels prepared from NFC have shown agreement with Eq. 7, where n-values reveal the gel strength (Naderi et al. 2014a; 2016; Lasseuguette et al. 2008). Gel strength is generally characterized by a large degree of independence of elastic moduli (elastic modulus (G´) and loss modulus (G´´) with respect to angular frequency (ɷ), which has more impact at higher frequencies, and higher flocculation within suspension can be revealed with frequency-dependent elastic moduli responses. Pääkönen et al. (2016) found that the shear modulus and viscosity of NFC suspensions decreased with the removal of xylan, a water-binding polysaccharide of hemicellulose, unevenly distributed on the fibril’s surface. Since the removal of xylan also decreased the water retention, it was proposed that a swollen sheath of xylan accounted for the shear modulus of the gel structures.
Aspect ratio of elongated particles
Subsequent investigators have extended Einstein’s predictions to non-spherical particles including ellipsoids (Marchessault et al. 1961; Mueller et al. 2010; Mewis and Wagner 2012) and stiff rods (Berry and Russel 1987; Dhont and Briels 2003; Boluk et al. 2011; Wu et al. 2017). The aspect ratio, i.e. the ratio of length (l) to diameter (d), has been shown to be a key variable governing the rheology of such suspensions. The aspect ratio of fiber suspensions has been predicted to have significant effects on suspension viscosity, even at sufficient dilution such that viscous effects are not affected by inter-particle collisions (Simha 1940; Araki et al. 1998).
For highly dilute suspensions of rods, in systems where the rate of particle Brownian rotation is fast enough to preclude significant alignment of the particles, the intrinsic viscosity can be estimated from (Onsager 1932; Weirenga and Philipse 1998),
![]() (8)
(8)
where r stands for the aspect ratio L/d.
At higher solids levels, effects of interactions between adjacent particles become significant, and it has been found that the following expression can be used to predict the relative viscosity, h/ho (Weirenga and Philipse 1998):
![]() (9)
(9)
The parameter L is the scale length, v is number density of rods, and b is a measure of the degree of freedom from “tube constraints” that prevent rodlike particles from turning around due to crowding by surrounding particles. Sato and Teramoto (1991) added a further term using a mean-field approach under the assumption of no entanglement:
![]() (10)
(10)
where D is the rotational diffusion coefficient.
To relate nanocellulose aspect ratios to observed viscosities, the fm term in Eq. 4 can be estimated from the gel crowding factor (see later discussion) (Celzard et al. 2009). Under the assumption that the alignment of the nanocellulose particles remains chaotic, the definition of the gel crowding factor gives the following,
fm = 64/[(2/3) (L/d)2] = 96 (L/d)-2 (11)
A key challenge in applying such an approach lies in the strong tendency of elongated particles to become aligned when exposed to flow, which is another topic to be discussed in this article. The take-away message at this point is that although Eqs. 4 and 11 appear to have suitable characteristics to enable one to estimate the effects of aspect ratio on suspension viscosity, as a function of volume fraction, such a calculation would require bold assumptions regarding the maximum packing density under the applied hydrodynamic conditions.
Chen et al. (2017) found that in a system containing both polyvinyl alcohol (PVOH) and CNC, the value of fm calculated based on CNC alone was 17.3%, which was much lower than the expected value based on percolation theory. The cited authors proposed that the downward shift was attributable to the space occupied by the loops and tails of adsorbed PVOH. The authors did not observe a corresponding downward shift of fm in the presence of CMC, and they attributed this to a general lack of adsorption of the CMC on the CNC under the conditions of testing. Another possibility is that the relatively stiff nature of CMC at low ionic strength favors flat adsorption onto cellulosic surfaces (Ueno et al. 2007).
Xu et al. (2013) define a related quantity fc, which they identified with the “onset of perculation”. This quantity was predicted to follow the relationship:
fc = 0.7(d/L) (12)
Hill (2008) suggested that a somewhat higher coefficient than 0.7 may be more accurate. Moberg et al. (2017) evaluated values of fc for a series of CNC and NFC suspensions that had been prepared with different aspect ratios and with sufficient negative surfaces charges to achieve excellent dispersion of the particles. Values of fc were found to range from 0.31 to 0.36 for two NFC samples. Higher values of fc in the range 0.75 to 1.92 were determined for various CNC preparations. It is tentatively proposed that the difference can be attributed to the relatively straight nature of typical CNC particles, compared to the curled shapes that are often assumed by NFCs. A non-straight shape in suspension implies a much lower end-to-end distance (Wierenga and Philipse 1998).
Flexibility
Although real fibers are flexible, many of the derivations related to the viscosity of suspensions have, for simplicity, assumed rigid rods. Ishii et al. (2011) found that the flexibility of nanocellulose particles (NFC or CNC) made an important contribution to their rheological behavior beyond the yield point, i.e. flow initiation of suspensions. The length of nanocellulose fibrils and surface charge affect flocculation, with shorter fibrils generally producing smaller agglomerates, and lower surface charge producing higher flocculation within the suspension matrix. Therefore, differences in equilibrium flocculation and/or agglomeration for the different nanocellulose systems depend on the solids content, with obvious strain dependence/hardening for highly flocculated MFC suspensions (Fall et al. 2011).
Switzer and Klingenberg (2003) considered a model that incorporated the bending of fibers. Flexibility generally reduces the observed rigidity of a suspension, compared to predictions based on rigid particles that are otherwise identical (Férec and Ausias 2015). Similarly, swelling of nanocellulose fibrils can reduce the friction between fibrils in a suspension, thus allowing their movement upon application of shear.
Batches of NCF that are produced with chemical treatment typically have higher surface charge and are generally more water-swollen and flexible than low-charged MFC produced by mechanical action alone. They therefore create less friction while in shearing conditions; as a consequence they tend to exhibit more pronounced decreases in viscosity parameters as a consequence of flow (Dimic-Misic et al. 2013b,c). Shear-thinning effects tend to be more pronounced, and the onset of shear thinning generally starts at lower applied shear stress (Keshtkar et al. 2009).
Iwamoto et al. (2014) were better able to account for the viscosity of NFC suspensions by assuming that flexibility made an important contribution. However, Tanaka et al. (2015) were unable to detect any significant contribution of fiber flexibility to the intrinsic viscosities of CNC or NFC suspensions. Thus, it would appear that the flexibility mainly affects systems in which nanocellulose entities are mutually interacting in flow, but maybe not so much when they are widely separated from each other.
Lubrication effects
Friction between contacting surfaces is believed to play an important role with respect to the elastic modulus and other strength characteristics of entangled fibrillar material (Lowys et al. 2001). According to Mewis and Wagner (2009), surface roughness can decrease frictional effects by preventing the close approach of the opposing surfaces. But on the other hand, roughness also can impede the sliding of one surface relative to the other, so the net effect may be hard to predict. Gallier et al. (2014) conducted simulations and showed that surface roughness and inter-particle friction can be expected to contribute significantly to the flocculation within the suspensions and also affect its rheological properties.
Lubrication effects were considered by Bououa et al. (2016a,b). The idea is that liquid medium can tend to hold solid surfaces apart from each other, thereby delaying contact and diminishing the development of frictional forces. As shown by Brenner (1974), such hydrodynamic interactions are expected to significantly affect rheological behavior. Under static or low shear conditions, beyond the yield point, the presence of gels – including nanocellulose suspensions of sufficiently high solids content – can exhibit diverse rheological behavior, depending on the surface charge and the water binding property of fibrils. In the case of high aspect ratio NFC, the application of strain under low shear (beyond the yield point) for continued periods can lead to structure ensemble orientation. The strong mutual electrostatic repulsion of the highly charge nanoparticles and the immobilization of the trapped interstitial water act together to create highly elastic structured zones, that are manifested as rheopectic behavior, i.e. a time-dependent increase in viscosity (Dimic-Misic et al. 2016).
Quantification of Resistance to Flow
Viscometers and rheometers serve various functions in science and in process monitoring. Rotational viscometers measure viscosity at fixed rotational speeds by driving a spindle immersed in the test fluid. By contrast, a rheometer is a device used for measuring the rheological properties over a varied and extended range of conditions. A rheometer can measure both the viscosity and viscoelastic properties of fluids, semi-fluids and solids. It can provide information on the following rheological properties:
- Viscosity as a function of shear rate, shear stress, time, or temperature
- Viscoelastic properties, such as storage (elastic) and loss (viscous) modulus with respect to time, temperature, frequency, and stress/strain
- Transient response-creep and recovery, relaxation modulus
There are two main types of rheometers: controlled strain rheometers and controlled stress rheometers. Controlled strain rheometers apply rotation and measure torque. Controlled stress rheometers apply torque and measure strain. The advantages of a controlled strain rheometer are that the rheological properties of stiff materials and solids can be measured, measurements can be made over a greater dynamic range, and better normal force and dynamic measurements can be made since sample strain is controlled. The advantage of a controlled stress rheometer is that the sample is not forced to move before measurement, enabling weak forces of interaction to be detected. Also, its mechanical design is simpler, and through software control, such devices can mimic controlled strain rheometers. Modern equipment often can perform both controlled-strain and controlled-stress analyses.
Rotational viscometers and rheometers are based in principle on the Searle method of measurement, in which a geometry of known surface area (bob, couette, plate) is in contact with a fluid sample that rests between the geometry and an adjoining surface. The device starts from rest and begins spinning at a preset rotational speed (shear rate). The spinning of the geometry is resisted (shear stress) by the fluid sample. This viscous drag results in a torque value, which can be measured mechanically. The viscosity is calculated from the torque measurement and shear rate. The shear rate is calculated from rotational speed and gap distance between the fixed surface and geometry. In addition to reporting viscosity at a single shear rate, rheometers enable continuous measurements under increasing and decreasing rates of shear to enable a rheogram to be produced. Rheograms are helpful in predicting the flow behavior of materials under several orders of shear and enable the shear thinning and flow recovery of materials to be examined.
Wall Depletion Effects
It is well known that, in simple shear flow, particles and macromolecules will tend to become depleted at the solid boundaries of flow (Chow et al. 1994; Barnes 1995; Mewis and Wagner 2012; Mosse et al. 2012). For instance, such “wall depletion” has been considered to be a serious issue by those wishing to quantify the rheology of macroscopic fiber suspensions (Bennington et al. 1990; Derakhshandeh et al. 2011; Moss et al. 2012). Figure 9 provides a schematic illustration, assuming couette-type (co-axial cylinder) flow under laminar conditions. Related observations have been reported in the case of nanocellulose suspensions (Saarikoski et al. 2012; Mohtaschemi et al. 2014b; Nechyporchuk et al. 2014, 2015; Saarinen et al. 2014; Kumar et al. 2016b; Naderi and Lindström 2016; Nazari et al. 2016). A variety of explanations for wall depletion have been advanced, and the situation can be summarized by noting that a relatively clear layer near the wall will result in a lower energy state during laminar shearing, i.e. an energetically favorable situation. Slippage effects at the walls of cylindrical-type viscometer devices often can be overcome, at least within certain ranges of experimentation, by installation of vanes or by roughening the walls (Bennington et al. 1990; Barnes 1995; Swerin 1998; Mosse et al. 2012; Mohtaschemi et al. 2014b; Nechyporchuk et al. 2014, 2015; Naderi and Lindström 2016).
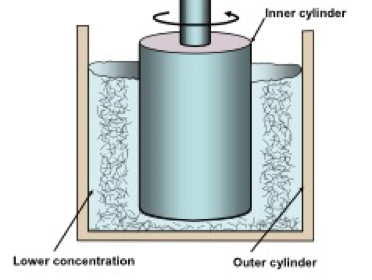
Fig. 9. Schematic illustration of depletion of suspended material at the walls (wall slip) when suspensions are exposed to laminar shear flow, especially when the cylinder surfaces are smooth and there are no vanes extending into the annular region
Avoiding apparent wall-slip, or more precisely solids depletion at the sample-wall interface, in such systems requires use of profiled surfaces or specific measuring geometry, e.g. a serrated surface in plate-plate geometry and a vane-in-cup spindle in cylindrical geometry (Mosse et al. 2012; Mohtaschemi et al. 2014a,b). During rheological measurements complicating interparticle interactions in the system are accompanied by those at the particle-geometry interfaces, inducing further instrumental limitations.
Rheological investigations of highly fibrillated cellulose systems have generally followed the classical demand for industrial applications, i.e. low to high shear viscosity and structure recovery. Such measurements may be well suited for the paper and board industry, for example, but for some applications extended low shear conditions are necessary, where it is favorable that the gel properties are preserved. For these applications where applied stress is necessarily below the yield stress, any required dewatering must occur within the initially linear viscoelastic region (LVE). Apparent wall-slip is one of the major challenging effects when measuring rheology of these materials, where the depletion of dispersed particles from the contact region with the measurement geometry walls leaves a liquid layer with dramatically lower viscosity than the bulk viscosity (Nechyporchuc et al. 2015; Nazari et al. 2016; Puisto et al. 2012a).
The magnitude of applied shear on fibrillar hydrogels in bob in cup geometry, without adopting the vane, was found to induce changes in floc structure and a strong wall-slip effect (Karppinen et al. 2012; Martoia et al. 2015), causing phase separation tendency and influencing the thixotropic properties (Dimic-Misic et al. 2015b; Puisto et al. 2012a,b; Nazari et al. 2016; Buscall 2010). The term bob in cup implies that a cylindrical solid rotor, which may have a flat or shallow pointed end, is rotating within a cylindrical cup, often with a narrow annular space. The effects of the electrosteric properties of suspension constituents, temperature of the mixture, and the consistency on the rheological properties were also studied. It was unsurprisingly observed that different systems displayed different rheological behavior. Such findings make it possible in principle to use the technique to probe these properties, albeit in a state requiring deconvolution of the multiple effects described above (Lasseuguette et al. 2008; Fall et al. 2011; Dimic-Misic et al. 2013b,c; Tanaka et al. 2014).
The fact that modifications of ordinary rheology-measuring devices often are needed to assess the effects of structures present in nanocellulose suspensions prompts a question of whether or not the resulting test data represent situations of practical interest in industrial applications. It is proposed here that the presence of highly uniform suspensions of nanocellulose, especially at solids levels where it is possible for cellulosic structures to fill the whole space, may be the exception rather than the rule. It is proposed that many industrially important processes will themselves be subject to the effects of wall depletion.
Shear Banding
The term “banding” refers to the development of periodic thickened regions and depleted regions relative to the axis of a couette-type viscometer apparatus (Ovarlez et al. 2009). It appears that the periodicity is related to the phenomenon of Taylor vortices (see Fig. 10), which develop when inertial effects start to become large enough to disrupt the purely laminar flow prevailing at lower velocities (Marcus 1984; Mohtaschemi et al. 2014b). According to Overlez et al. (2009) the phenomenon has its roots in a competition between floc destruction due to flow and floc building and strengthening over the course of time. Such a dynamic situation favors the segregation of relatively strong flocculated network fragments, separated by areas in which the solids are either depleted or more dispersed into individual particles.
Several authors have reported band formation when nanocellulose suspensions have been evaluated in the gap between a rotating cylinder and a stationary cylinder (Karppinen et al. 2012; Mohtaschemi et al. 2014b; Nechyporchuk et al. 2014; Saarinen et al. 2014; Dimic-Misic et al. 2015c; Martiola et al. 2015). However, due to lower centripetal force, there should be less chances of shear band formation at relatively lower speed of rotating cylinders.
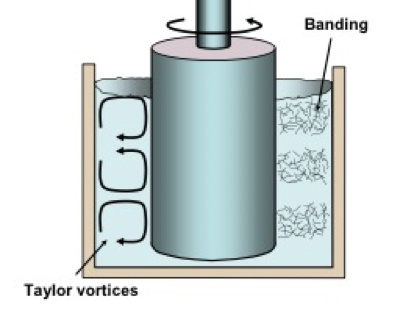
Fig. 10. Schematic diagram of couette transitional flow in a rotating viscometer, illustrating the development of Taylor vortices, and the further tendency for formation of bands enriched with suspended particles
MFC and NFC suspensions are thixotropic and prone to form areas of shear banding within the gel suspension. The fibrils of MFC and NFC have both crystalline and amorphous regions (Usov et al. 2015), which both play a role in low-shear induced structuration, as was addressed in previous publications (Dimic-Misic et al. 2015b).
When these fibrillar suspensions are exposed to ultralow shearing for a prolonged time, an observed rheopectic response suggests the development of fibril-fibril collective structure arising from the axially symmetric shear that leads to fibril alignment (Dimic-Misic et al. 2014; Usov et al. 2015). Depending on the fibril charge and aspect ratio, this alignment can result in the conditions ripe for structure condensation (Dalpke and Kerekes 2005; Naderi et al. 2016a; Dimic-Misic et al. 2013c).
Although a vane spindle in cup geometry decreases the effect of apparent wall-slip, shear banding may be present between regions of different stress. This is a manifestation of the thixotropic nature of such systems, i.e. the viscosity depends on the time of application of different levels of shear. The described conditions can lead to the formation of intra-structural regions of different viscosity and thus flow properties, which, when having in mind the highly crystalline nature of the fundamental elements in NFC or MFC, act to as a precursor for aligned planar structures (Martoia et al. 2015; Nechyporchuk et al. 2014, Nazari et al. 2016).
In nanocellulose suspensions it appears that the tendency of band formation can be enhanced by both the tendency for alignment in flow and the tendency for formation of entangled structures. Dimic-Misic et al. (2015c) proposed that the essentially one-dimensional NFC becomes structured as a two-dimensional band of twisted fibrils under the prolonged influence of low shear that is below the yield point.
Viscosity vs. Solids Content
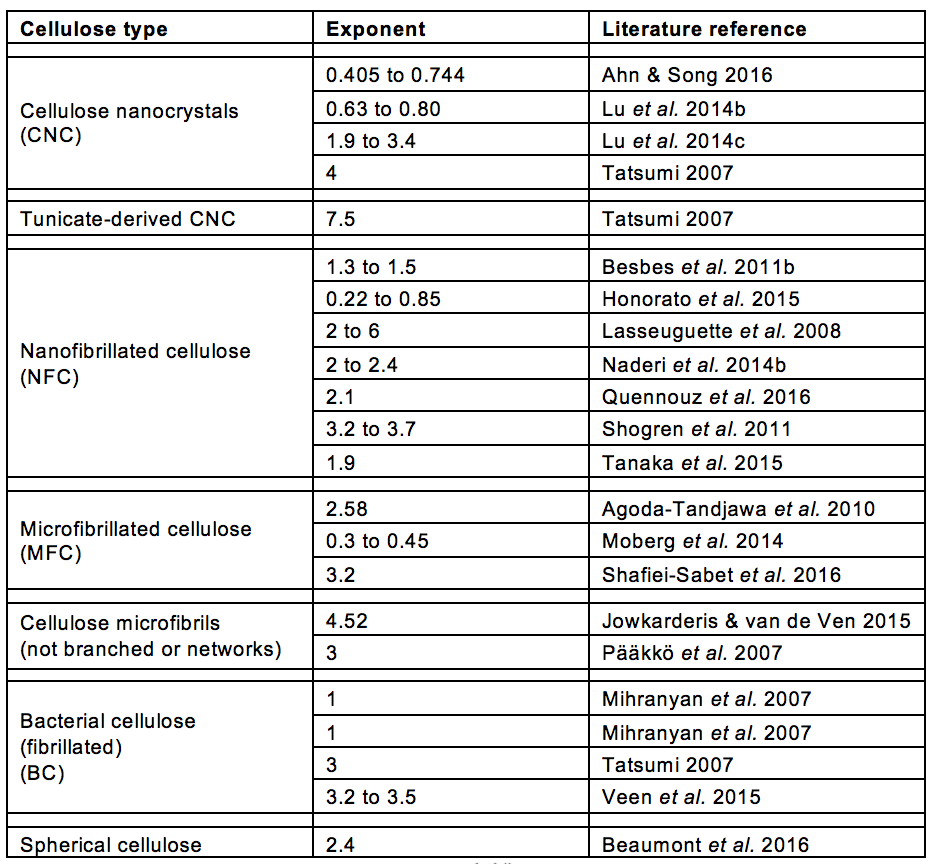
Because of such phenomena as lubrication effects, entanglements, irregular shapes, and fiber flexibility, among others, the relationship between measured viscosity and nanocellulose solids content is likely to be irregular, not necessarily conforming to versions of Eqs. 1 through 12. Table 6, which provides a subset of data from Table A, shows that a range of different values have been observed for the exponent in Eq. 5.
Under flow conditions, an increase of shear rate tends to enhance both the aggregation and fragmentation of MFC (Saarikoski et al. 2012; Saarinen et al. 2014). In the case of NFC, increased shear rate results in deformation of the predominantly gel-like structure, resulting in flow curves showing hysteresis and thixotropic behavior (Illa et al. 2013; Puisto et al. 2012a,b). In complex colloid systems, such as suspensions of NFC or MFC, the final equilibrium state is governed by a number of parameters describing hydrodynamic shear stress that distorts or pulls structures apart, which are often incorporated into the modeling of thixotropy (Coussot et al. 2002, Divoux et al. 2013, Dullaert and Mewis 2006; Hill 2008; Mewis and Wagner 2009).
Inspection of Table 6 shows, first of all, that the value of n determined in different studies of nanocellulose suspensions varied widely. Many studies reported values of n in the range of about 1.5 to 6. Certain studies reported much lower values (Mihranyan et al. 2007; Lu et al. 2014b; Moberg et al. 2014; Honorato et al. 2015; Ahn and Song 2016), and the reason for this difference is not readily apparent. The most interesting results were those of Tatusmi (2007) who showed, under the same conditions of testing, that tunicate-derived CNC, having a very high aspect ratio, yielded a much higher value of n in comparison to more usual CNC particles in suspension.
Table 6. Reported Exponents* for Viscosity-Solids Results for Aqueous Suspensions of Nanocellulose
* Exponents refer to the following equation: ![]()
To provide some additional insight into the value of n, data collected from 40 studies considered in the present review are compiled in Fig. 11. In each case, the data correspond to the viscosities (in Pa×s) vs. percent solids, evaluated at a shear rate of 1 s-1 in an aqueous solution having water-like viscosity (not dominated by polyelectrolytes). As shown in the graph, MFC and NFC suspensions (represented by red diamonds) generally exhibited much higher viscosity, at a given solids level, than the CNC suspensions (shown with dark blue squares. This difference is understandable in terms of the much higher aspect ratio of typical highly fibrillated samples, compared to CNC. The bacterial cellulose results (green circles), of which there were only a few data sets reported in the specified manner, generally fell within the range occupied by the highly fibrillated cellulose suspensions. Another point of reference, when considering Fig. 11, is the viscosity of pure water, which can account for the fact that the most dilute suspensions of CNC did not show viscosity values below about 0.001 Pa×s.
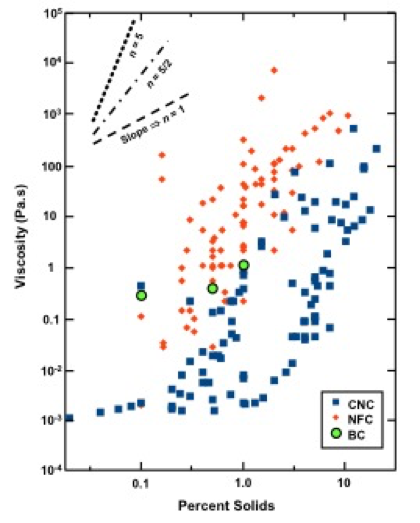
Fig. 11. Representation of viscosity-solids data from 40 studies for 1% solids nanocellulose suspensions, under the conditions of a shear rate of 1 s-1 and water-like viscosity of the aqueous solution
It is worth noting that the results corresponding to CNC appeared to follow two contrasting “tracks” in the solids range between about 0.5% and 5%. Two factors appear to be responsible for this separation of the data. On the one hand, relatively high viscosity of CNC suspensions at low shear rates has been observed in studies involving CNCs having relatively high aspect ratio (Lu et al. 2014a; Tang et al. 2014; Wu et al. 2014). Other authors reported relatively high low-shear-rate viscosities of CNC suspensions when the aqueous conditions favored the presence of net attractive forces between the cellulosic surfaces, leading to the development of structures (Li et al. 2015b; Lewis et al. 2016). The gels have inherently high viscosity at the start of shearing, but once the shearing has started, their viscosities drop. Also, if shear rate is constant, (low shear rate for longer periods of time) due to the thixotropic properties, their transient viscosity slowly decreases, or it increases in the case of longer fibrils. The various systems represented in Fig. 11 also would have involved a wide range of ionic strengths, surface charges, and other details of experimentation.
The trend lines at the upper left of the figure represent three possible values of the exponent in Eq. 5. Note that the middle slope, with n = 5/2, represents the trend predicted by Einstein for non-interacting, equal spheres at very low concentration. The steepest slope corresponds to the maximum slope discussed by Mueller et al. (2010). The lower slope, shown here for comparison, represents an exponent of 1.
The high viscosity values at low suspension solids and broad variability between reported values emphasizes two of the greatest challenges for advancing the application and use of these materials in commercial applications. The broad variability causes concern for product consistency, and high viscosity values at low suspension solids imply high costs for pumping and shipping.
Particle Interactions in Flow
Orientation in flow
For low consistency and non-interacting solid suspensions, particles will have a random arrangement due to Brownian motion of the particles. However, if the particles are interacting, or at relatively high solids concentrations, the particles can aggregate, become aligned, or form or network structure, even forming gel structures having yield behavior, meaning that the viscosity becomes infinite as the shear rate approaches zero. Flow can influence each of these phenomena.
When suspensions of elongated particles are exposed to flow, several related phenomena can occur, including preferential orientation, shear-thinning, and the formation of flocs or entangled groups of fibers. Such phenomena are well known for suspensions of macroscopic fibers (Rahnama et al. 1995; Cui and Grace 2007; Férec et al. 2009; Phan-Thien 2016). For instance, a tendency for cellulosic fibers to become oriented in the direction of flow, which is often perpendicular to the shear fields during laminar flow, has been observed for papermaking pulp fibers (Mason 1954). Alignment in shear flow is brought about by the fact that each half-cycle of shear-induced rotation of an elongated fiber involves a speeding up and a slowing down, where the slowest turning coincides with the flow-aligned condition (Phan-Thien 2016). These phenomena have been carefully studied in laminar shear flow regimes, within which it is possible to precisely predict the rotational, “tumbling” motions of individual fibers (Mewis and Wagner 2012). Berry and Russel (1987) predict that the aligning effects of flow can be reinforced by Brownian motion. Pryamitsyn and Ganesan (2008) predicted a screening effect of Brownian motion, which interacted with the effects of shear in suspensions of rods.
More recently, many authors have reported evidence of orientation of nanocellulose suspensions exposed to laminar shear (Orts et al. 1995, 1998; Ebeling et al. 1999; Bercea and Navard 2000; Noroozi et al. 2014; Hakansson et al. 2016). Ebeling et al. (1999), who used small angle synchrotron X-ray scattering, found that a shear rate of 5 s-1 or higher was sufficient to orient CNCs in a sheared suspension. At lower values of shear rate there was some alignment of larger clusters of CNCs, acting as a group, but such clusters were dispersed by intermediate shear, and the CNCs were oriented as individual particles in the higher shear range.
Shear-thinning
Mongruel and Cloitre (1999) and Switzer and Klingenberg (2003) established that shear thinning behavior, in the case of suspensions of macroscopic fibers, could be attributed to the break-up of clusters and that Newtonian flow behavior was observed at shear rates sufficient to prevent the existence of such clusters. Shear thinning behavior has been widely reported also in the case of nanocellulosic suspensions. Many such cases are listed in Table 7. Based on such reports it is clear that shear-thinning can be regarded as a characteristic feature of nanocellulose suspensions, if the solids content is high enough.
Table 7. Shear Thinning Behavior Reported for Aqueous Suspensions of Nanocellulose
Key: CNC = cellulose nanocrystals; NFC = nanofibrillated cellulose; MFC – microfibrillated cellulose; BC = bacterial cellulose; MCC = microcrystalline cellulose
An interesting question, which might be the subject of future work, is the degree to which shear thinning effects in nanocellulose suspensions can be attributed to particle alignment, which was discussed in the previous section. When particles become aligned, they can be more easily packed into smaller volumes. Likewise, if the volume and amount of particles remain constant, then the mixture may behave as if it is less crowded when there is increasing alignment. Such effects may explain why Bercea and Navard (2000) observed a transition from dilute behavior to gel behavior at a concentration of about (d2/L2) in CNC suspensions under slow shearing conditions, but the transition was shifted to much higher values (approximately d/L) at higher shear rates of shearing. Oguzlu et al. (2017) used similar logic to explain increases in suspension viscosity when the polyelectrolyte carboxymethylcellulose (CMC) was added to nanocellulose suspensions.
Thixotropic systems, i.e. those that exhibit reversible shear-thinning behavior, often show a characteristic time of recovery (Barnes 1997). Thixotropy is important because it can greatly impact the leveling properties of a material after application or during metering. Bercea and Navard (2000) described such processes of recovery in liquid-crystal suspensions of CNC as “fast” in contrast with liquid crystal polymer solutions. Derakhshandeh et al. (2013), in the case of CNC suspensions, found the characteristic recovery time to be generally less than a second and dependent on the shear rate. Orts et al. (1995) found that the relaxation effect occurred more rapidly for shorter microfibrils having aspect ratios near 30. In related work, Le Goff et al. (2014) showed that minutes were required to complete the gelling of suspensions of relatively long CNC particles. In general, the relaxation effects appear to be related to Brownian motion, which tends to restore the random orientation of particles within a characteristic time period.
History-dependent and Irreversible Effects
Quasi-irreversible, non-equilibrium effects have been reported in aqueous suspensions of nanocellulose (Puisto et al. 2012b; Derakhshandeh et al. 2013; Mohtaschemi et al. 2014b). According to Mohtaschemi et al. (2014b) such behavior of NFC suspensions implies that viscosity measurements made at relatively low shear rates can be regarded as non-unique and dependent on the flow history. Whereas ideally thixotropic systems can be counted on to return to their previous steady-state viscosity, at a specified shear rate after a delay time, the concern here is about systems that appear to remain trapped in non-equilibrium states, possibly due to non-equilibrium aspects of either the forming or the breaking down of structures.
Different terminology appears to be in most frequent use when referring to clusters of papermaking fibers vs. clusters of nanocellulose entities. The terms “floc” and “flocculation” are widely used to describe the clustering of papermaking fibers, which typically have aspect ratios of about 100 (Hubbe 2007). Articles dealing with related phenomena in suspension of NFC, MFC, and BC more often have used words such as “entangled” and “entanglements” (Lowys et al. 2001; Pääkkö et al. 2007; Gong et al. 2011; Zhong et al. 2012; Benhamou et al. 2014; Lu et al. 2014b,c; Naderi et al. 2014a; El Miri et al. 2015; Jowkarderis and van de Ven 2015; Li et al. 2015b; Chen et al. 2016b; Martoia et al. 2016; Paximada et al. 2016). Though it is likely that many of the same mechanisms will apply, the use of different terminology is possibly justified by the higher aspect ratios that are typical for NFC and MFC. For instance, it appears likely that NFC clusters may be bound together by the wrapping of fibrillar elements, whereas such a mechanism has not been reported for flocs of ordinary papermaking fibers.
The length of individual fibrils, which together with fibril width determines the aspect ratio, controls fibril alignment and structuration under controlled shear rate conditions. For example, liquid crystalline domains can form under application of ultralow shear, resulting in a high stress response at low strain. Their chiral nature provides a long-range connectivity between long fibrils, such that, over extended time, the aligned bundle of fibrils effectively twist into a rope-like structure; in such situations the trapped gel water tends to be expelled from the interfibril space (Usov et al. 2015; Dimic-Misic et al. 2017a,b).
Crowding factor analysis
Before elongated cellulose entities can form clusters, they must first collide with each other. Mason (1950) introduced the concept of predicting the likelihood of collisions among fibers in a suspension by computing the volumes obtained when each of the fibers rotates about the center of the spherical volume that it occupies. This idea was formalized by Kerekes and Schell (1992), who proposed the definition of a crowding factor. This can be expressed as in Eq. 13,
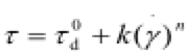 (13)
(13)
where Cv is the volume concentration, L is the fiber length, and d is the fiber diameter. It has been observed in such studies that fiber suspensions having similar values of crowding factor tend to have similar levels of fiber flocculation under similar conditions of flow.
As noted earlier, Celzard et al. (2009) proposed a “gel crowding factor.” The condition of gel formation was observed at a crowding factor value of 60. That is the value above which stirred papermaking fibers will tend to form noticeable and persistent flocs. The cited authors noted that such a “gel crowding factor” is similar in many respects to concepts of a percolation threshold (Philipse and Wierenga 1998; Wierenga and Philipse 1998; Zimmermann et al. 2004; Moon et al. 2011; Mewis and Wagner 2012; Saarikoski et al. 2015; Cao et al. 2016; Meree et al. 2016; Mukherjee et al. 2016; Chen et al. 2017), which can be defined as the solids level in which uniformly distributed suspensions of fibers will form an essentially continuous structure. As noted by Celzart et al. (2009), results calculated by models identified by the term “percolation” are in general agreement with older research in which the term “effective medium theory” had been used and where the particles were modeled as elongated ellipsoids (Landauer 1978). It should be kept in mind that the gel crowding factor, as just described, does not take into account the known effects of electrostatic repulsions (see later discussion).
Formation of fiber flocs and entangled nanocellulose
Persistent floc structures in papermaking pulp suspensions can be held together merely by friction and by the tendency of the fibers to regain their straightness due to their elastic properties. As described by Parker (1972), the fibers can become locked into floc structures as their elastic nature causes them to try to regain the initial straightness that they had prior to the application of shear. The mechanism is illustrated in Fig. 12, which shows some of the simplest floc structures of this type that can be formed. Raghavan and Douglas (2012) proposed that, in order to be effective, such a mechanism requires that the solid particles must be sufficiently long, stiff, and unbreakable. In the case of suspensions of kraft fibers, as used in papermaking, Bennington et al. (1990) concluded that the elastic forces induced by fiber bending contributed to floc stability, but that some other factor, such as attractive forces of surfaces in contact, must also play a role. In principle, such flocs can remain stable under sufficiently gentle shear conditions even in the absence of net attractive forces between the solids (Mason 1950, 1954; Meyer and Wahren 1964; Parker 1972; Swerin et al. 1992; Kerekes 2006; Hubbe 2007).

Fig. 12. Examples of very simple floc structures that can be held together mechanically. A: flocs held together by elastic forces within bent fibers, along with frictional effects; B: Concept of entanglement involving long, flexible fibrils
Since NFC, MFC, and bacterial cellulose can have aspect ratios greatly exceeding 100 (see Table 5), such floc structures can be expected to develop during stirring of the suspensions coexisting with repulsive forces in case of highly charged surfaces. This may be important in terms of rheology, since the resistance to motion can be influenced by whether or not there are fluid-filled gaps between adjacent floc structures. In some cases, rather than having a suspension of nanocellulose particles, the rheology of a suspension might more appropriately be modeled as a suspension of flocs dispersed in a liquid phase or in a gel-like matrix.
Researchers studying nanocellulose suspensions and mixtures have reported observations of agglomeration induced by mixing when the solids level is higher than a certain level, which can be attributed to the formation of a gel-like structure (Iotii et al. 2011; Cao et al. 2016). Cao et al. (2016) confirmed such findings by using ultrasonication to redisperse the agglomerates; the redispersed system provided higher strength of reinforced cement mixtures, as would be expected for a more uniformly distributed network. Likewise, Saarikoski et al. (2012) showed that MFC in sheared suspensions may consist of multiple entities of agglomerates suspended in gel-like matrix that can be separated by application of sufficiently high shear stress sufficient to initiate flow in the suspension, i.e. a yield point. The yield point of nanocellulose suspensions is therefore dependent on both consistency and the size of agglomerates. The effective size is governed by factors including surface charge, swelling, and length of fibrils (Dimic-Misic et al. 2017a).
Due to the very slender nature of NFC, it is reasonable to consider whether or not the elastic restorative forces within the fibrils are high enough to make a significant contribution to floc persistence. In other words, maybe the fibrils within NFC or MFC are not stiff enough for the elastic forces to make a significant contribution. To the best of our knowledge, the needed analysis has not been reported.
Evaluation of rheological properties of intact gel structures
MFC and NFC at sufficiently high solids content tend to form solid-like aqueous hydrogels structures. The rheological characterization of such structures is complicated due to the diverse characteristics of the fibrillar components. This makes it necessary to develop different measuring protocols, and the results often are best described as apparent quantities. The indefinite nature of the results leads to difficulties when trying to establish comparable analytical results (Mohtaschemi et al. 2014a,b, Martoia et al. 2015). To tune the rheological behavior of such systems as a means of enhancing their processability, it is necessary to understand both their viscoelastic and flow behavior in terms of the surface charge and morphology of the highly fibrillated cellulose particles. The rheological characterization of NFC- and MFC-based systems is complicated due to the diverse properties and interactions between both the fibrillar and colloidal components, with non-linear flow curves displaying thixotropy and a difficult-to-define yield stress, which in turn depends on gelation (surface charge) and flocculation (aspect ratio colloidal stability) (Fall et al. 2011; Saarikoski et al. 2012; Naderi and Lindström 2015).
Oscillatory measurements are widely used to examine the contributions of solid-like (elastic) and liquid-like (viscous) interactions on the flow characteristics and mechanical properties of materials having gel-like characteristics. This mode of testing is also referred to as dynamic mechanical analysis (DMA) (Schlesing et al. 2004). DMA can be performed under shear, torsion, compression, or tension with a dynamic stress or strain instrument. Rheometers measure the response of a material to the application of shear forces. Dynamic mechanical tests performed under compression, tension, and torsion enable the mechanical properties of a material, such as tensile strength, elongation, stiffness, and compressibility to be studied. Figure 13 illustrates schematically some common test fixtures used to perform these studies.
While much work has focused on the effect of nanocellulose morphology and interactions on the rheology of suspensions, only a few researchers have coupled rheological and mechanical property findings. Vesterinen et al. (2010) showed a correlation between the rheological and dynamic mechanical properties of microfibrillar cellulose suspensions. Measurements of the viscoelastic properties of a microfibrillar cellulose in water suspension and the dynamic mechanical properties of paper made from the suspensions showed that the strength properties of the paper sheets could be estimated from the viscoelastic behavior of the dilute suspensions. Differences in the yield behavior observed in rheological oscillatory tests were correlated to the strain behavior of the paper sheets in dynamic mechanical testing. A conclusion that can be drawn from these two works is that both the rheological and mechanical properties of a material depend on the compatibility of its components.
Fig. 13. Basic DMA test configurations. A: Compression; B: Tension; C: Bending; D: Shear
There also are some relevant findings in cases where polyelectrolytes made a relatively large contribution to the viscous effects. For example, Yang et al. (2013) examined the mechanical and viscoelastic properties of cellulose nanocrystals reinforced polyethylene glycol nanocomposite hydrogels. By measuring the mechanical responses of the hydrogels under periodic strains, quantitative information on the viscoelastic and rheological properties of the hydrogels were obtained. The results indicated that the mechanical reinforcement and energy dissipation effects were coupled. Energy dissipation via the rearrangement of CNC/PEG interactions was found to facilitate the toughness and extensibility of the polymer nanocomposite hydrogels. Excessive loading of CNCs was found to disturb the homogeneity of the networks, resulting in a reduction in the mechanical properties of the composites.
It is anticipated that future researchers may compare and correlate rheological and mechanical properties. Such correlations may be pertinent, for instance, in applications of cellulosic materials as reinforcing fibers in extruded films for packaging (Hubbe et al. 2017), extruded resins for 3D printing, and injection molded parts. Further work pertaining to the mechanical properties of nanocellulose hydrogels and polylactic acid/MCC composites, respectively, were reported by Mathew et al. (2005) and Frensemeier et al. (2010); however, rheological measurements were not made in those studies.
Let us assume that a given suspension of highly fibrillated cellulose exists as a gel structure. Let us further assume that after the application of moderate force, which can distort the structure, the gel will tend to revert to its initial shape due to stored elastic energy within the nanocellulose structure, plus the persistence of contact points among the cellulose surfaces. As already mentioned, such contact points might be attributable to entanglement of the nanocellulose (Lowys et al. 2001; Raghavan and Douglas 2012; Zhang et al. 2012; Arola et al. 2013; Benhamou et al. 2014; Lu et al. 2014b,c; Naderi et al. 2014a; El Miri et al. 2015; Paximada et al. 2016). Another contribution to relatively persistent contact points among the cellulose surfaces may be net attractive forces, such as those that might result from the addition of salt (Lowys et al. 2001; Beck and Bouchard 2016).
Yield Point Phenomena
The presence of contiguous structures within an aqueous mixture of nanocellulose can be expected to have a major effect on rheological properties. The term contiguous is used here to indicate that the nanocellulose particles form a continuous system of connections, which fills the volume being tested. Araki (2013) suggested the term “structural viscosity” to highlight the essential relationship between such structures and the elastic component of resistance to movement. Frensemeier et al. (2010) suggested the use of conventional Maxwell models (spring and dashpot type) to model the stress-strain behavior of contiguous gels composed of bacterial cellulose.
Much of the emphasis in the literature related to the rheology of nanocellulose suspensions has been focused on theories that can account for quasi-equilibrium conditions, steady-state conditions, and structures that are assumed to be relatively uniform. Such a focus can be justified by the availability of well-accepted theories, which have been found to be useful for understanding the rheology of a wide range of fluids. But nanocellulose suspensions – especially in the case of NFC and bacterial cellulose – may be especially susceptible to entanglement and other non-equilibrium effects. It follows that a focus on non-equilibrium effects is needed. This section will consider such issues as the breakup of gel structures and the rheology of suspensions of clusters of broken-up structures. For example, Naderi et al. (2014a) proposed that the rheology of carboxylated NFC can be understood in terms of a suspension of a severely entangled structure that has been partly disentangled.
According to Mueller et al. (2010), once shear-thinning has occurred in a stirred suspension of relatively high solids content, the system may once again exhibit a linear relationship between stress and strain. Such quasi-Newtonian behavior might be explained by the presence of particle-free shear planes within the mixture. It appears that such fragments of broken networks often remain suspended in suspensions. So rather than acting as a suspension of individual particles, the system acts as a suspension of the partly-broken fragments of the initial gel networks. This situation is illustrated schematically in Fig. 14.
Fig. 14. Schematic view of anticipated transformation of a network-like structure into individual entangled fragments, possibly with some individual fibrils, as a result of continued agitation
Breakup of structure
The manner of breakup of flocculated cellulosic suspensions has been studied both for papermaking pulps and for nanomaterials. In the case of papermaking pulps (Björkman 2003a), break-up of fiber flocs, as a result of agitation of the suspensions, is likely to take place in zones parallel to the greatest local compression of the mixture. Photographs of suspensions flowing in expanding or narrowing channels exhibited narrow zones of interruption between adjacent areas of a contiguous (continuously connected) fiber network. The orientation of those fiber-free zones contrasted sharply when comparing the expanding and narrowing channels. Both the acceleration or slowing of flow, as well as wall effects, appeared to be involved. Tensile stresses within the floc structure were found to easily bring about zones of separation, whereas compression gave rise to a “rope” structure featuring a higher solids content of cellulosic material from which the water had been squeezed out (Björkman 2003b). In follow-up work, Björkman (2006) showed that the viscosity of realistic fiber suspensions could be modeled by treating separated flocs as the suspended entities. The model was set up to allow water to flow in and out of such flocs, which may split and fuse, shrink, or swell. Chen et al. (2002) found that fiber flocs formed at an intermediate shear stress, but that at yet higher shear stress the flocs again became well dispersed. Damani et al. (1993) noted that after stirring, a fiber suspension was transformed into fragments of fiber floc structure, as well as individual fibers in suspension.
In the case of nanocellulose, Martoia et al. (2015) observed that the broken-down structures of sheared NFC suspensions were sensitive to the details of their preparation. NFC produced with enzymatic hydrolysis exhibited “drastic mesostructural changes”, whereas NFC prepared after TEMPO oxidation did not. Such observations are consistent with attraction between cellulosic surfaces, leading to a solid-like structure that can fracture in an irreversible manner. The TEMPO oxidation would provide sufficient electrostatic repulsion to overcome the attraction between approaching surfaces.
Due to the complex nature of flow curves and their thixotropic character, fitting the steady state data to a Herschel-Bulkley yield stress model, as is usually used for nanocellulosic materials, can result in misconception of the obtained dynamic yield stress (τdo) values (Mohtaschemi et al. 2014a,b; Nazari and Bousfield 2016). Therefore, the rheological effect of the physical and colloidal interaction within the sample matrices consisting of solid constituents is investigated with oscillatory measurements (Naderi et al. 2014a; Dimic-Misic et al. 2016b; Kumar et al. 2016b). In such work the rheology of samples is studied without breaking down the microstructure in the gel-like system, thus minimizing the effect of apparent wall slip/depletion. For estimating “static yield” stress (τs0), oscillatory measurements are used, within the linear viscoelastic (LVD) region, obtained with serrated plate-plate geometry (Pääkkönen et al. 2016). Figure 15 provides an example of both steady shear and oscillatory rheometric results for the same system, NFC in the solids range between 2% and 7% (Nazari et al. 2016). As shown in this example, an effect analogous to ordinary shear thinning is often observed when increasing frequencies of oscillation are applied to nanocellulose suspension.
Oscillatory measurements were also used for determination of the apparent yield stress, which was previously defined as static yield point, τs0 (Dalpke and Kerekes 2005; Dimic-Misic et al. 2016). The static stress component (τs0) is described by
![]() (14)
(14)
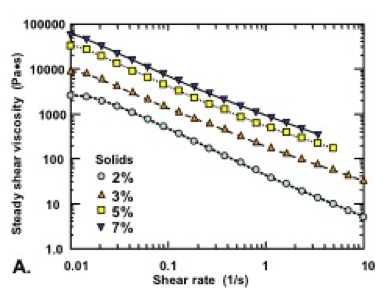
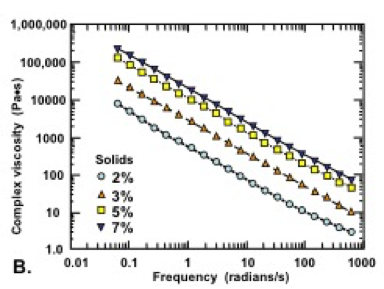
Fig. 15. Viscosity of 2, 3, 5, and 7% (by mass) suspensions of NFC as measured by (A) steady shear and (B) oscillatory rheometry; figure redrawn from the results by Nazari et al. (2016)
During the strain sweep measurements, the elastic modulus G´ is recorded as γ increases. The maximum static stress at the critical strain γc is taken to correspond to the static yield stress τs0, and is determined as the first point of deviation from the linear stress (τs)-strain (γ) curve occurring at the critical strain γc (Horvath and Lindström 2007). Figure 16 provides an example showing how the rheological behavior of a real cellulose fiber suspension (plotted points) can be represented by a model that assumes a single strain-dependent yield point (Horvath and Lindström 2007).
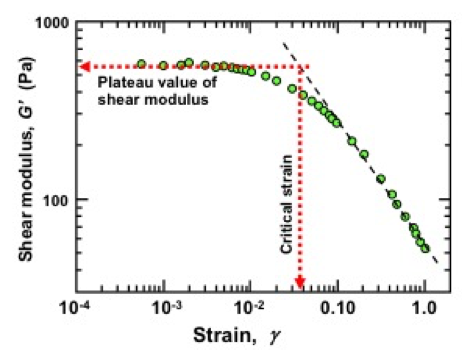
Fig. 16. Schematic illustration contrasting static vs. dynamic yield stress evaluation. Figure redrawn from the data published by Horvath and Lindström 2007)
For the determination of dynamic yield stress (τd0) one takes η ( ) flow curves, applying the Herschel-Bulkley equation, Eq. (15), given by (Dimic-Misic et al. 2013a,b, 2016b; Pääkkönen et al. 2016):
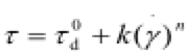 (15)
(15)
The flow curve parameters k and n are related to the time-dependent response of gel matrix of NFC suspensions regarding the morphology of NFC and surface. Lower surface charge systems will tend to have lower water binding properties and repulsion between fibrils, leading such systems to be more flocculated (higher k); in such cases the yield point will be naturally higher due to the higher stress needed to break up the flocculated matrix and put a system in a flow. The static yield stress (τs0), determined from unbroken suspension matrix, (within LVE) is always larger than dynamic yield stress (τd0) (Dimic-Misic et al. 2013b; Pääkkönen et al. 2016).
Extensional Viscosity
Various applications in which nanocellulose suspensions might be used involve squeezing the mixtures through screens, nozzles, or other such circumstances in which the fluid is required to converge or diverge during its passage (Petrie 1999; Dimic-Misic et al. 2015a). Such “extensional flow” has been found to lead to high levels of resistance to flow in the case of polymer solutions (Rodriguez-Rivero et al. 2014). Sufficient flow intensity (e.g. pressure applied) has been shown to be effective in reducing the molecular mass of dissolved polymers (Nguyen and Kausch 1992; May and Moore 2013). Since nanocellulose elements tend to have high aspect ratios, as is the case for soluble polymers, it is reasonable to suspect that high levels of extensional viscosity may result, whether or not soluble polymers are present in the mixture. Indeed, Dimic-Misic et al. (2015a) used extensional viscometry to characterize the effect of ionic strength in MFC and NFC pigment-containing suspensions. It is notable that some salt is invariably present in industrial-scale applications of pulp, even after washing; such salt can affect extensional viscosity of nanocellulose-based coatings. Moberg et al. (2014) carried out similar work and found that sodium chloride first increased the extensional viscosity, but higher concentrations promoted agglomeration,
Filament rheometers, which measure transient extensional viscosity as a function of strain, operate under similar principles. Two types of filament rheometers are filament stretching extensional rheometers (FISER) and capillary break-up extensional rheometers (CaBER) (McKinley and Sridhar 2002). FISER rheometers generate a cylindrical filament by uniaxially stretching a material at a constant strain rate by imposing an exponential endplate displacement. The tensile force and midpoint radius of the filament are measured to compute the transient viscosity. For a CaBER a small volume of sample is injected between two circular endplates. The endplates are quickly separated over a short distance, during which time the initial axial deformation of the sample happens. As the plates are separated, a laser micrometer monitors the change of the filament midpoint diameter with time. The test is performed under controlled temperature conditions. The transient apparent extensional viscosity is calculated by dividing 2 times the surface tension of the fluid by the change of filament diameter as a function of time.
COLLOIDAL CHEMISTRY OF RHEOLOGY & NANOCELLULOSE
Geometrical Aspects of Colloidal Interactions
Models to estimate forces of interaction
When solid objects in aqueous suspension approach each other to within about a few nanometers, increasingly strong forces of interaction develop (Liang et al. 2007). Such forces can be expected to influence the rheological behavior of suspensions that contain particles (Russel 1978). In cases where the materials, shapes, and suspending media are exactly known, such forces can be predicted (Israelachvili 2011). However, the irregular and sometimes relatively unknown nature of nanocellulose surfaces generally require the use of simplified geometric models to estimate the magnitudes of repulsive or attractive forces, which are in addition to the lubrication effects considered in the previous section. Studies of short-range interactions within suspensions are typically modeled either by assuming interactions between parallel planar surfaces or by assuming that at least one of the surfaces can be locally modeled as a sphere or cylinder surface, within the region of close approach between the objects (Israelachvili 2011). The sphere-sphere, and sphere-plane simplified models are closely related to the situation of interactions between cylinders approaching each other in a non-parallel fashion (Sridhar et al. 1997).
Surprisingly, the review of the literature turned up only one recent study in which the researchers had attempted to calculate forces between nanocellulose particles in suspension and to relate the results of those calculations to rheological phenomena. Oguzlu et al. (2017) employed the well-known principles of colloid science to estimate repulsive and attractive components of interactive force. The cited article provides a demonstration of how some of the principles to be described below can be applied to specific cases.
The main classes of short-range forces that develop between solids present in aqueous suspension have been discussed elsewhere (Hubbe and Rojas 2008; Eichhorn 2011; Israelachvili 2011), so only a brief mention will be made here. Many studies have shown that the net force between solids in aqueous media can be modeled as the sum of attractive London dispersion (van der Waals) forces plus electrostatic forces. According to Russel (1978), short-range forces of attraction can be expected to play a key role governing the rheology of suspensions of solids. For instance, in work related to carbon nanofiber suspensions in a polymeric medium, Bounoua et al. (2016a,b) used van der Waals interactions as a key factor in their modeling to account for the yield stress of carbon nanofiber suspensions. However, such forces appear to have received relatively little emphasis in the literature related to the rheology of nanocellulose suspensions.
As noted by Gudarzi et al. (2015) the total force between two identical charged spheres or plates often can be best described by a summation of van der Waals force (FvdW), the double layer force (Fdl), as well as additional attractive forces (Fatt) as follows:
F = FvdW + Fdl + Fatt (16)
In the cited work, the additional attractive forces were attributed to multivalent cationic species.
If one also assumes absolute smoothness and completely uniform composition (which is not actually possible due to the finite size of molecules), then the near-range London-dispersion component of the van der Waals attractive forces can be modeled rather simply as (Hubbe 1984; Bowen and Jenner 1995; Israelachvili 2011),
![]() (17)
(17)
or as
![]() (18)
(18)
where the coefficient A in these equations is the Hamaker constant, R is the radius used in modeling the contact zone, and h represents the effective distance between the surfaces, according to the model. Since one is usually attempting to fit real data, in which the surfaces are rough and the composition might not be uniform, etc., the value of h can be used as a fitting parameter (Hubbe 1984). Values that have been determined for the value of A for cellulose immersed in an aqueous solution have been given in the range of 8.0 to 9.9 x 10-21 J (Bergstrom et al. 1999). More advanced models to account for roughness effects while estimating colloidal forces between solids were reviewed by Walz (1998).
Another major class of short-range forces having a dominant effect on the behavior of suspensions of finely divided materials is electrostatic forces, which are also called “double layer” forces (Hiemenz and Rajagopalan 1997; Liang et al. 2007). The electrostatic interaction energy between equal plates, both assumed to have the same uniform charge density, is given by (Hiemenz and Rajagopalan 1997),
![]() (19)
(19)
where Y is the electrostatic component of interaction energy per unit area between the plates, no is the concentration of ions in the solution, k is the Boltzmann constant, T is absolute temperature, go2 is the square of the surface excess of ions (i.e. the surface charge), k is the reciprocal length parameter defined in Eq. 21, and d is the distance between the surface of the plates (modeled as being completely smooth). A corresponding relationship can be derived for the energy of interaction between surface of adjacent perfect and equal spheres,
![]() (20)
(20)
where R is the effective radius of the spheres, and here d is taken as the closest point between the spheres. It is worth noting that Eq. 20 can be used to estimate the double layer interaction energy between a sphere and a flat surface by doubling the value of R.
The k -1 term in Eqs. 19 and 20 corresponds to the effective range of electrostatic forces within an aqueous solution, a quantity that is sometimes called the thickness of the ionic double layer. Its value, in units of length, is given by,
k -1 = [ Si (zi2ni) 4p e2 / (e kT) ]0.5 (21)
where zi is the valence of ions opposite to that of the charged body of interest, ni is the concentration of that ion, e is the electron charge, e is the dielectric constant of water, k is the Boltzmann constant, and T is the absolute temperature (Hiemenz and Rajagopalan 1997).
Many researchers have carried out energy-vs.-distance calculations based on a summation of attractive London dispersion forces and repulsive ionic double layer forces. Figure 17 depicts a commonly predicted circumstance for cases in which all the surfaces have the same sign of charge (as is often the case for cellulosic surfaces). Such a complex functional relationship between energy and distance arises because of the very different distance-dependencies expressed in Eqs. 17 and 19 (for interaction between two planes) or in Eqs. 18 and 20 (for interaction between spheres or a sphere and a wall) when considering the summation of attractive London dispersion forces and repulsive electrostatic forces. 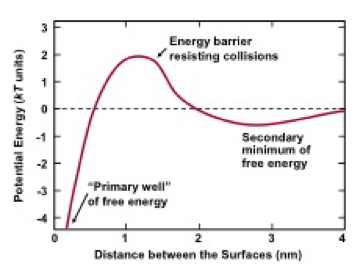
Fig. 17. Illustration of the type of energy-distance curve that is often calculated for systems in which like-charged solid surfaces are interacting in an aqueous suspension
Additional components of force, including effects of water structure (Israelachvili and Wennerstrom 1996; Israelachvili 2011), and polyelectrolyte effects (Claesson et al. 2005) have been considered. Because the effects of water structure are hard to predict and because the morphology of the cellulosic materials are often very complex, there has been a striking lack of attention to quantitatively predicting the net interactive forces or energies of surface interactions in nanocellulose suspensions.
Friction and roughness
Various investigators have shown the value of including frictional effects when modeling the rheological properties of fiber suspensions (Tatsumi et al. 1999; Switzer and Klingenberg 2003; Tatsumi et al. 2008; Férec et al. 2015). Researchers have shown that frictional effects can make important contributions to the viscosities and yield stresses observed in nanocellulose suspensions and gels (Gallier et al. 2014).
Effects of small-scale roughness of cellulosic surfaces can be regarded as a barrier to close approach of the main parts of the surfaces. Since the surfaces are impeded from coming together closely, strong forces of attraction, in particular, would fail to fully develop (Mewis and Wagner 2012). The situation regarding repulsive forces is less clear, however, since the points of roughness holding the main surfaces apart might be regarded as fulfilling that role. As noted by Gallier et al. (2014), fine-scale roughness also can be expected to contribute to resistance to sliding between contacting solid surfaces. So, the net effects of roughness on frictional effects in nanocellulose suspensions are inherently difficult to predict.
Charged Groups and Nanocellulose Suspension Viscosity
General effects
Surfaces bearing the same sign of charge in aqueous suspensions tend to repel each other, and such repulsions are understood to affect the viscosity of suspensions in various ways. Also, the presence of charged groups has been reported to be responsible for the stability of certain types of nanocellulose suspensions. Here the word “stable” means that a suspension remains well dispersed, as individual suspended particles, throughout the period investigated by a set of researchers. Araki (2013) attributed the stability of cellulose nanocrystals to the presence of charged groups, e.g. sulfate half-ester groups. Nanocrystals produced by HCl hydrolysis lack the stability in suspension of those isolated by H2SO4 hydrolysis or when CNC is phosphorylated. This is because the HCl-produced CNC lacks charged groups on its surface (Araki et al. 2000). The introduction of charged groups was found to markedly decrease the viscosity (Araki et al. 1999). Taheri and Samyn (2016) reported finding the lowest viscosity when the zeta potential indicated the greatest negative charge of highly fibrillated cellulose in suspension. Apart from aspect ratio and morphology, charged surfaces could be another explanation for lower viscosity of CNC compared to NFC at same solid concentration.
There are two main ways in which sufficiently strong repulsive forces between surfaces can be expected to affect suspension viscosity. First, by tending to hold the surfaces apart from each other, the frictional effects mentioned in the previous subsection can be decreased (Tatsumi et al. 1999). In other words, the repulsive forces act as a kind of lubricant, causing the surfaces to slip past each other rather easily rather than to become pinned to each other at points of roughness as the surfaces move past each other. Secondly, especially when the solids level is very high, the repulsive forces give the effect of making the suspension seem more crowded (Bergenholtz et al. 2002; Studart et al. 2007). As will be discussed later, the overlapping of electrical double layers can contribute to increased viscosity, and the effective thickness of double layers decreases with increasing ionic strength.
Effects of charge levels present on ordinary cellulosic material
The strengths of the repulsive forces will be affected by the density of the chargeable groups and the extent of their dissociation. Negatively charged groups already present in common cellulosic materials were discussed earlier. Horvath and Lindström (2007) observed a trend of decreased flocculation of cellulosic fibers in increasing negative charge of the surfaces. Likewise, as noted by Agoda-Tandjawa et al. (2010), the uronic acid groups present in the hemicellulose content will tend to reduce the viscosity of nanocellulose suspensions.
Effects of pH on suspension viscosity
Except when the charges are due to strong acids, such as sulfate or sulfonate, the degree of dissociation of negative groups on cellulose-based surfaces will be strongly affected by pH. Pääkkö et al. (2007) observed decreasing viscosity of a nanofibrillated cellulose suspension with increasing pH in the range 2 to 10, which is consistent with dissociation of the carboxylic acid groups. By contrast Agoda-Tandjawa et al. (2010) observed no pH effect in the range 4.5 to 9; the lack of effect was tentatively attributed to a much lower solids content in the cited work.
The expected effects of pH are illustrated in Fig. 18. In principle, when the pH is well below the pKa value of the carboxylic acid groups at the cellulose surface, those groups will be in their protonated (nonionic) form, leading to an absence of electrostatic repulsive forces between the surfaces. Accordingly, in relatively strongly acidic solution there will be a net attraction, resulting in either a strong network or separate clusters of nanocellulose. By contrast, at relatively high pH, the repulsion induced by negative charges on the surfaces will tend to disperse the material in the suspension.
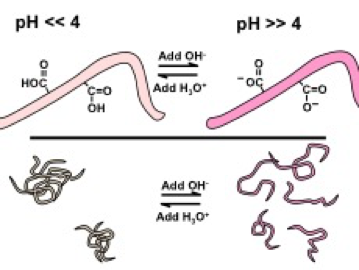
Fig. 18. Schematic view of the effect of low vs. high pH on the charge and degree of inter-fibril adhesion and network formation or clustering
Sulfate groups
Araki et al. (1998, 1999, 2000) observed thixotropic effects in suspensions of uncharged cellulose nanocrystals, whereas time-independent rheological properties were observed for negatively charged nanocrystals that had been prepared with sulfate groups. Those results are consistent with electrostatic repulsion, which was sufficient to inhibit sticking collisions among the cellulosic surfaces.
Further evidence of the effectiveness of sulfate groups relative to interactions between nanocellulose particles in suspension was reported by Araki (2013). Cellulose nanocrystals that were stabilized by such groups showed birefringence (see also Beck-Candanedo et al. 2005), whereas those prepared by digestion in HCl did not. The effect was attributed to sufficiently strong inter-particle repulsion to induce coherent alignment of the crystals in suspension. Shafiei-Sabet et al. (2013) reported that the density of sulfate groups on CNCs affected transitions from isotropic suspensions to liquid crystal suspensions, and subsequently to gelled form.
Ioelovich (2014) showed that conditions of sulfuric acid treatment also can be optimized so as to produce highly fibrillated materials, having a high contribution to viscosity. This is done using cold concentrated H2SO4 in the presence of strong agitation.
Although, as shown by the articles cited in this subsection, sulfate groups on nanocellulose surfaces can be highly effective as stabilizers, viscosity reducers, and cellulose-modification agents, such groups are susceptible to hydrolysis. Beck and Bouchard (2014) showed that the hydrolysis reaction, leading to a loss of the charged groups, is promoted by increasing temperature, lowering of the moisture content, and either acidic or alkaline conditions. Therefore, to avoid losing their negative charge capability during storage, it is recommended to prepare, dry, and store sulfate-stabilized CNC in their neutral salt form rather than in their protonated form. Lewis et al. (2016) reported removal of sulfate groups as a means of gelling CNC suspensions. A procedure has been developed for accurate determination of the sulfur content of CNC (Beck et al. 2015).
Derivatization of cellulosic surfaces with negatively charged groups
Further increases in dispersion stability and/or reductions in viscosity can be achieved by chemical derivatization, which can be used to reach higher negative charge densities (Naderi and Lindström 2016; Nechyporchuk et al. 2016; Heggset et al. 2017). For instance, the viscosity of cellulosic fiber suspensions can be decreased by carboxymethylation (Beghello and Lindström 1998). However, Naderi et al. (2016a) observed higher viscosity when cellulose fibers were carboxymethylated, compared with fibers treated in other ways to impart increased negative charge. The effect was attributed to the swelling effect resulting from the effective increase in negative charge character, leading to more rapid delamination and fibrillation. In another study it was shown that adding salt (sodium chloride) to the carboxymethylated nanofibrillated cellulose caused significant reduction in the viscosity of suspension when concentration of NaCl was greater than 1 mM (Naderi et al. 2014a). A likely explanation is that the suspension became agglomerated, such that the observed viscosity was dominated by the particle-free zones of water between the agglomerates. Horvath and Lindström (2007) observed strong dispersing effects and weaker network strength when carboxymethylcellulose (CMC) was grafted onto the surfaces of cellulosic fibers. Naderi and Lindström (2016) found that grafting with CMC yielded NFC suspensions with time-independent rheological behavior.
TEMPO oxidation
Oxidation mediated by the 2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPO) radical species has been found to give rise to specific conversion of the C6 group of cellulose to the aldehyde, and subsequently under suitable conditions to the carboxylic acid form (Saito et al. 2006; Isogai et al. 2011). Many researchers, as shown in Table 8, have reported results for the viscosity of nanocellulose suspensions prepared with TEMPO oxidation. In summary, this type of treatment has the potential to achieve high levels of carboxylation, providing a negative surface charge while minimizing damage to cellulose nanostructures or molecular mass of the cellulose. As shown, TEMPO-mediated oxidation was found generally to increased dispersibility of nanocellulose (Hirota et al. 2010; Li et al. 2015a), which is consistent with increased electrostatic repulsion between the surfaces. Suspension behavior was sensitive to salt (Crawford et al. 2012; Fukuzumi et al. 2014), which again is consistent with basic theories of colloid science. Higher charge, induced by TEMPO treatments, also facilitated the production of nanocellulose by mechanical means (Loranger et al. 2012a; Mishra et al. 2012a; Kekalainen et al. 2015). The latter findings are consistent with the greater compatibility of the carboxylated surfaces with the water phase.
Periodate oxidation
Oxidation with periodate offers an alternative way to prepare negatively charged cellulose surfaces (Kekalainen 2014b).

Fig. 19. Reaction scheme for periodate-assisted oxidation of cellulose to first yield pairs of aldehyde functions, which can be further oxidized to carboxylic acid groups
Table 8. Rheological Observations in TEMPO-oxidized Nanocellulose Suspensions
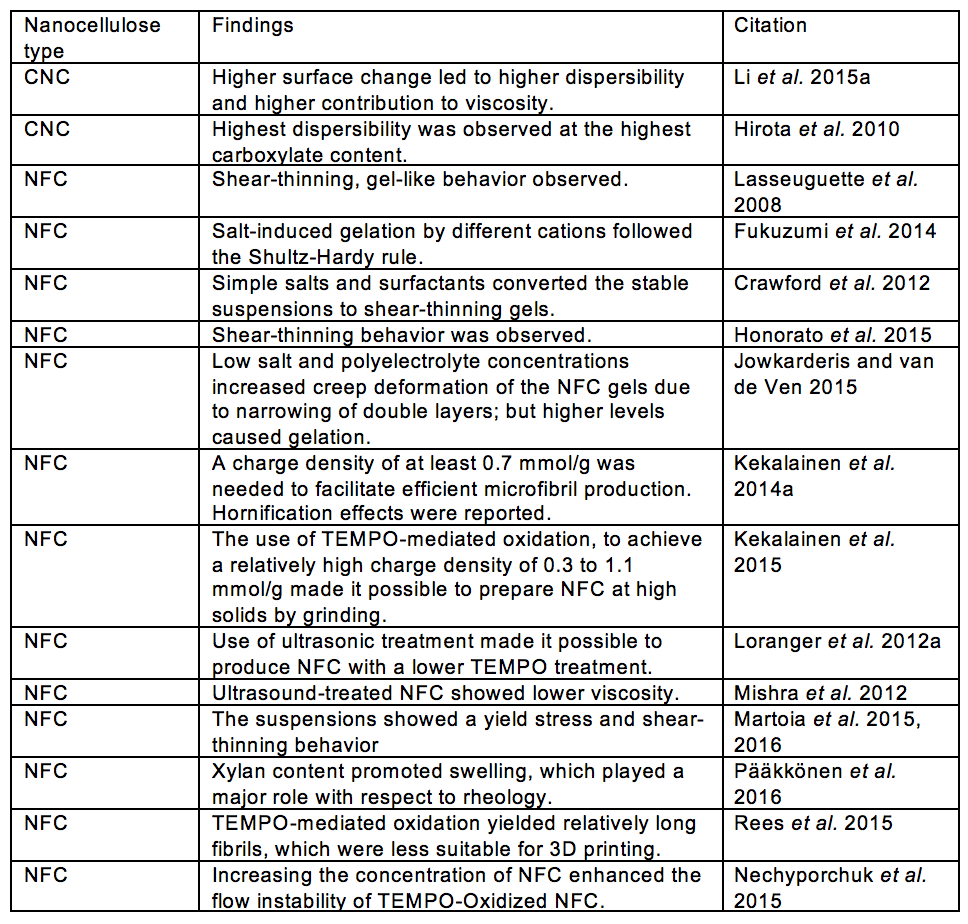
As shown in Fig. 19, treatment of cellulose with periodate initially yields aldehyde groups at the C2 and C3 positions using sodium metaperiodate, and the further action of an oxidizing agent such as sodium chlorite can lead to carboxylic acid groups in those positions.
Because periodate treatment tends to open up the anhydroglucose ring (Chen and van de Ven 2016), such oxidation tends to do more damage to the cellulose degree of polymerization, compared to the TEMPO-mediated oxidation just described. The cited authors showed that, depending on the time of treatment, it was possible to achieve sterically stabilized nanocellulose having a high dialdehyde content. A decreasing viscosity with increasing treatment was attributed to preferential attack at amorphous regions of the cellulose, leading eventually to isolation of crystalline regions. Rees et al. (2015) took advantage of the tendency of periodate treatment to favor shortening of the nanocellulose, since they found that such nanocellulose had a low suspension viscosity that was suitable for 3D printing.
Phosphate derivatization
Araki et al. (2000) appear to have introduced the use of phosphate treatment as a way to induce a negative charge to cellulosic surfaces, promoting their dispersion. They employed mixtures of phosphoric acid and urea. The negative charges at the cellulosic surfaces tended to overcome thixotropic effects, presumably by keeping the cellulosic surfaces from coming into contact with each other. Camarero Espinosa et al. (2013) prepared phosphorylated CNCs. Naderi et al. (2016b) described phosphate treatment of cellulosic surfaces as industrially attractive. Treatment of cellulose with solutions of sodium dihydrogen phosphate was followed by drying, curing for one hour at 150 oC, and then passage through a microfluidizer. Figure 20 illustrates the reaction of hydroxyl groups of cellulose and sodium dihydrogen phosphate. As shown here, the reaction yield can be defined based on the amount of removed water. Rheological properties were described as being similar to suspensions of NFC prepared in other ways.
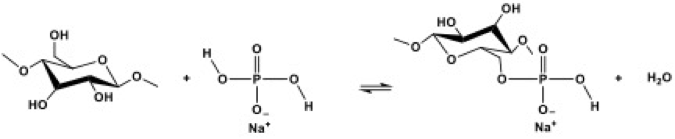
Fig. 20. Reaction scheme for sodium dihydrogen phosphate and cellulose
Cationic modifications
Interesting rheological effects have been shown when cellulosic surfaces have been rendered cationic. For instance, Hasani et al. (2008) observed enhanced gelation when CNC was rendered cationic by reaction with glycidyltrimethylammonium chloride. Likewise, Karppinen et al. (2011) evaluated the effect of cationic methacrylate polymers in gel formation within the microfibrillated cellulose (MFC) suspension. Chaker and Boufi (2015) reacted NFC with the same cationization agent and observed shear-thinning behavior. The viscosity increased with increasing treatment level, especially when comparing the levels 300 and 760 meq/g. While the authors proposed that the enhanced viscosity was attributable to hydrogen bonding, the full results of the study suggest that the effect may have been due to more extensive dispersion and out-stretching of the nanomaterial. Such an explanation is consistent with the finding, reported in the same article, that both cationic and anionic modification of the NFC enhanced the reinforcement potential of the NFC in a polyvinyl alcohol matrix.
Stabilization by Adsorption of Charged Species
Rheological effects due to adsorption of various species from solution often can be interpreted in terms of frictional interactions between the surfaces. Lower inter-fiber friction has been predicted in cases where the presence of extended water-loving polymers at the cellulosic surface tend to impede close approach of the surfaces (Beghello and Lindström 1998; Zauscher and Klingenberg 2000; Lowys et al. 2001; Tatsumi et al. 2008). In other words, steric stabilization (Araki et al. 2001) is expected to overcome attractive interactions, leading to lower or eliminated yield stress. Such effects can be achieved by adding either dispersants or surfactants.
Dispersants
The term “dispersant” will be used here to denote a highly charged, multivalent species having the ability to adsorb onto surfaces in a suspension and render sufficient charge density to give a dispersing effect. As illustrated in Fig. 21, a dispersant can keep the surfaces from colliding and sticking together.
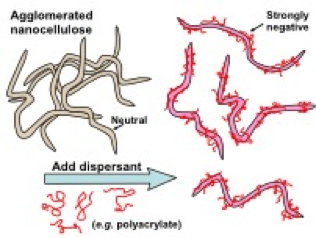
Fig. 21. Schematic illustration of dispersant action
One of the most widely studied dispersants for the stabilization of aqueous nanocellulose suspensions is carboxymethylcellulose (CMC). Dispersing effects for nanocellulose using CMC have been reported (Lowys et al. 2001; Ahola et al. 2008; Vesterinen et al. 2010; Dimic-Misic et al. 2013a, 2014; Butchosa and Zhou 2014; Sorvari et al. 2014; Naderi et al. 2015b,c; Veen et al. 2015; Ahn and Song 2016; de Kort et al. 2016; El Baradai et al. 2016; Nazari and Bousfield 2016; Schenker et al. 2016; Chen et al. 2017). Because CMC shares the same backbone structure with cellulose, it is possible that adsorption can involve alignment of the CMC chains with the cellulose chains (Pönni et al. 2012). Such a mechanism may explain the effectiveness of CMC in such applications. Lowys et al. (2001) found evidence that CMC addition decreased the frictional interaction between the nanocellulose surfaces. Lower gel strength was reported by Sorvari et al. (2014) and Veen et al. (2015). Schenker et al. (2016) observed only small effects on suspension viscosity upon addition of CMC, but time-dependent effects were diminished, which is consistent with less attractive interaction between the cellulose surfaces.
Reported higher viscosity, upon addition of CMC (Vesterinen et al. 2010) is likely due to bridging effects of the polyelectrolyte, since the effect exceeded what could be explained by a contribution of the CMC to viscosity of the suspending medium. A bridging effect, to explain similar observations, was proposed by Zhong et al. (2012).
Surfactants
Surfactants can be defined here as molecules having both hydrophilic and hydrophobic groups, and various researchers have shown that surfactant usage can affect the rheological properties of nanocellulose suspensions. Missoum et al. (2012a) reported that addition of the anionic surfactant sodium dodecyl sulfate (SDS) decreases the viscosity of NFC suspensions over a wide range of shear rate. Results were rationalized by modeling the molecular organization at the surfaces. Quennouz et al. (2016) found that effects of addition of various surfactants to NFC suspensions was dependent on the level of addition. At low addition levels, gel modulus was generally increased. Higher addition levels of charged surfactants led to agglomeration, resulting in a loss of the contiguous structure of the NFC at the solids levels considered. As a consequence, the observed resistance to flow decreased. Notably, however, incorporation of an ethylene-oxide hydrophilic segment in an anionic surfactant avoided the agglomerating effect and the related lowering of measured viscosity.
Electroviscous effect
An electroviscous effect can be defined as an increase in viscosity attributable to ionic charges on the surfaces of suspended particles (Sherwood 1981; Russel 2009; Mewis and Wagner 2012). There appear to be two main contributions to the electroviscous effect, which have become known as primary and secondary (Wiersema and Philipse 1998). The primary electroviscous effect can be attributed to distortion of the ionic double layers due to flow, whereas the secondary effect is attributable to overlap of double layers on adjacent surfaces. The secondary electroviscous effect has been predicted to play a dominant role once the solids content is high enough that pair-wise interactions between particles become common (Wiersema and Philipse 1998).
The mechanism of the secondary electroviscous effect appears to involve the excluded volume concept as already mentioned (Bergenholtz et al. 2002; Studart et al. 2007). When elongated particles are essentially “held apart” from each other by repulsive forces between the surfaces, the suspension behaves as if it is more crowded, and the measured viscosity is likely to be higher.
Several researchers have suggested that an electroviscous effect might account for some aspects of nanocellulose suspensions. For instance, Jowkarderis and van de Ven (2014), Shafiei-Sabet et al. (2014), and Beck and Bouchard (2016) noted a decrease in the viscosity of CNC suspensions upon addition of small amounts of electrolyte, and they attributed the effect to the compression of the electrical double layer thickness. On the contrary, Boluk et al. (2011), who also mentioned an electroviscous effect, found that the addition of NaCl to sulfate-stabilized CNC particles in suspension resulted in a much higher measured viscosity, which would be more consistent with a model of coagulation (see later).
The term “immobilized water” was used by Benhamou et al. (2014) to denote a related effect that depended upon solids level of TEMPO-mediated NFC suspensions. At lower extents of TEMPO treatment, the cited authors proposed that the gel structure was governed primarily by entanglement, but at higher durations of TEMPO treatment the structure became dominated by its contained water. These observations are consistent with the overlap of double layers and osmotic swelling of the material. Likewise, Dimic-Misic et al. (2013c) pointed out that the degree of swelling of the nanocellulose determined the amount of occupied volume, leading to crowding effects and accounting for rheological effects.
Magnetic field effect
Kim and Song (2015) reported large increases in the measured viscosity of CNC suspensions with increasing magnetic field strength. Results were attributed to a tendency of charged nanoparticles to line up perpendicular to an applied field. Because magnetic fields are relatively easy to apply in industrial processes, more research in this area may be helpful.
Steric Stabilization
Steric stabilization can be defined here as inhibition of contact between the surfaces of suspended particles due to the presence of macromolecular tails or loops extending from the surfaces outward into the solution (Araki 2013). In the case of an aqueous solution, it could be added that those macromolecular segments would be hydrophilic. Araki (2013) reviewed studies in which CNC suspensions had been stabilized either by electrostatic or steric mechanisms. It was proposed that the following factors need to be in place to achieve strong steric stabilization in such systems: high molecular mass, high level of stabilizer, and high solvation of the macromolecular loops and tails.
Steric stabilization can most easily be brought about through adsorption of either a water-soluble polymer or a long-chain surfactant compound. Figure 22 provides a schematic view, illustrating how the tails and loops of adsorbed hydrophilic polymers could be expected to impede the close approach of cellulose fibrils. Some authors who have employed CMC as a stabilizer have regarded steric stabilization as a likely contributing mechanism (Butchosa and Zhou 2014). Agoda-Tandjawa et al. (2012) suggested that effects of low-methoxyl pectin could be attributed to such effects. Similar findings were reported by Hiasa et al. (2016). Ferrer et al. (2016) proposed that similar effects can be caused by residual polysaccharides and lignin present in microfibrillated soybean hulls. Results of quartz crystal microbalance (QCM) analysis, considering the dissipation of energy, provided supporting evidence of loosely-bound polyelectrolyte segments following adsorption of CMC or xyloglucan on cellulosic nanofibrils surfaces Ahola et al. (2008). Other evidence in support of the steric stabilization mechanism is a finding by Korhohen et al. (2014) that the stabilizing effect of anionic polyacrylamide for MFC increased with increasing molecular mass. In many such situations, however, it is difficult to draw a clear line between the expected purely electrostatic effects and those attributable to extended polymer segments.
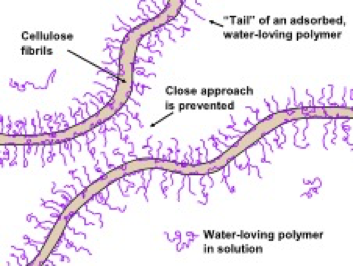
Fig. 22. Schematic illustration of steric stabilization, resulting from the adsorption of water-loving polymers onto cellulose fibrils and tended to prevent their close approach to each other
Steric stabilization also can reasonably play a key role is cases where hydrophilic polymer chains are grafted to cellulosic surfaces (Araki et al. 2001; Araki 2013; Naderi and Lindström 2016). For example, the reduced viscosity reported by Horvath and Lindström (2007) could be reasonably attributed to steric stabilization.
DESTABILIZATION AND NANOCELLULOSE RHEOLOGY
Net attraction between cellulosic surfaces in suspension is another chemical-based contribution that can be expected to affect rheology. In principle, such effects can be attributed to inherent attractive forces (e.g. van der Waals forces; see earlier discussion), reduction of repulsive forces, and various less studied effects, such as flow-induced destabilization. The discussion that follows considers factors that tend to decrease the electrostatic repulsion between the solid surfaces, thus allowing the attractive forces between the cellulosic surfaces to dominate.
Coagulants
A coagulant can be defined as an ionic compound, opposite in charge to suspended particles, thus tending to decrease repulsive electrostatic forces. The coagulant can accomplish this goal mainly in two ways – by decreasing the range of the repulsive forces (double layer compression) and by decreasing the effective charge of the surfaces (specific adsorption).
Simple salts, such as NaCl, act mainly in a non-specific manner. The influence of salt ions on the effective range of electrostatic forces can be calculated based on Eq. 21, as discussed earlier. The quantity k -1 in that equation is proportional to the distance over which electrostatic forces maintain a given level of influence. In principle, with increasing concentration of simple salts, the range and effectiveness of electrostatic forces are decreased, and by default the attractive van der Waals forces can become dominant, leading to agglomeration.
Figure 23 provides a schematic illustration of how the addition of salt can be expected to affect the interaction energy of solids suspended in aqueous solution. Again, it is assumed that all the solid surfaces have a negative charge. As shown, the expected effect of salt addition is to decrease the range and strength of the electrostatic repulsion forces. When sufficient salt has been added (sometimes called the critical coagulation concentration), the solid surfaces can come rapidly into contact, depending on just diffusion and convection. The result can be either a gelled structure or an uneven mixture of agglomerated matter, depending on the solids level, history of shear, and other details.
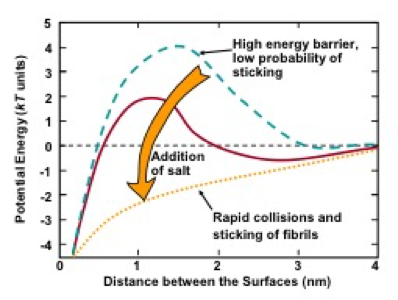
Fig. 23. Schematic illustration of how salt addition can affect the net energy of interaction between like-charged surfaces in aqueous solution, bringing about rapid “sticking” collisions
Effects of monovalent ions on the rheology of nanocellulose and related suspensions have been widely reported (Kratohvil et al. 1969; Ono et al. 2004; Agoda-Tandjawa et al. 2010, 2012; Lu et al. 2014a; Moberg et al. 2014; Shafiei-Sabet et al. 2014; Qi et al. 2015; Sim et al. 2015; Beck and Bouchard 2016; Qiao et al. 2016; Tanaka et al. 2016; Xu et al. 2017). Such effects have been attributed, in many cases, to induced aggregation among the suspended particles above a critical concentration of the ions (Fukuzumi et al. 2014; Lu et al. 2014a). Researchers have proposed that increases in viscosity or yield stress were due to the development of net-attractive contacts within the mixture (Lowys et al. 2001; Agoda-Tandjawa et al. 2012; Sim et al. 2015). In other cases the initial decrease in viscosity, with increasing salt concentrations in a low range, have been attributed to a thinning of ionic double layers at the solid surfaces (Jowkarderis and van de Ven 2015; Shafiei-Sabet et al. 2014; Beck and Bouchard 2016). Since the particles (which may be rods or fibrils) are not being held so far apart from each other, the system does not behave as if it is so crowded. But further addition of salt eventually brings about agglomeration of particles, since the double layer forces are no longer strong enough to keep the suspended matter from contacting each other. The attractive van der Waals forces become dominant, which can lead either to a fully gelled mixtures or to suspensions of clusters of particles. Moberg et al. (2014), Oguzlu et al. (2017), and Wu et al. (2017) noted complicated effects, depending on the level of salt addition. There was increased viscosity at a lower range of salt addition followed by agglomeration and lowered viscosity at a higher range of salt addition. Such observations are consistent with an initial space-filling structure of connected cellulosic particles at the lower range of salt addition. A higher level of salt, especially in the presence of flow, would induce agglomeration, and then the cellulosic structures would no longer fill the available volume without spaces between the fragments.
Fall et al. (2013) proposed a markedly different model to account for the effects of added NaCl to suspensions of carboxymethylated NFC. Rather than just decreasing the double layer thickness, it was proposed that the main effect was to associate with carboxylate groups (counter-ion condensation), leading to a de-facto reduction in surface charge. The specific adsorption was predicted by the authors to take place because of the high density of charged groups on the nanocellulose. The justification for the model appears sound, and it can be expected that future researchers may attempt to follow up with this type of analysis in related systems involving suspensions of cellulosic materials.
Multivalent ions and rheology
When considering the effects of divalent ions, e.g. Ca2+, a critical issue is whether or not the nanocellulose suspension also contains an anionic polyelectrolyte such as CMC. Let us first consider the results of studies in the absence of polyelectrolytes. Several studies have shown that much lower concentrations of divalent ions were sufficient to bring about coagulation or to change the rheology of nanocellulose suspensions, compared to monovalent salt treatment (Kratohvil et al. 1969; Fukuzumi et al. 2014; Jowkarderis and van de Ven 2014; Sim et al. 2015). Agoda-Tandjawa et al. (2012) also described the presence of calcium ions mixing with low-methoxyl pectin (LM pectin) raised the viscosity of microfibrillated cellulose suspension, leading to a gel composite. Such relationships often follow the Schulze-Hardy rule, which states that the critical coagulation concentration is proportional to the negative sixth power of the valence of the added ion that is opposite in charge to the suspended particles (Kratohvil et al. 1969; Hiemenz and Rajagopalan 1997; Fukuzumi et al. 2014). On the other hand, multivalent cations such as Al3+ and Al12(OH)24AlO4(H2O)127+ (Bottero and Fiessinger 1989) can be expected to form complexes at the surfaces of anionic nanocellulose particles, even reversing the surface charge if the dosage is sufficient (Strazdins 1989).
Chau et al. (2015) studied the effects of cation valence and ionic size on the structures formed in suspensions of sulfate-stabilized CNC. A unique finding of the study was that different ionic conditions yielded different “wall thickness” characteristics in which CNCs lined up in parallel within gel structures. The authors proposed that the presence of the cations promoted side-to-side binding of the CNC particles. Both the complex modulus of elasticity and the mesh size were positively correlated with cation valence and cation radius (within a class of valence).
Cationic polyelectrolytes
Lu et al. (2014b) studied the effects on rheology of adding a cationic polyelectrolyte to a CNC suspension. The cationic polymer appeared to participate in the formation of a structure that incorporated the CNC particles. Addition of NaCl weakened such associations and also tended to reduce the crowding in the suspension due to decreased double layer thickness. Further work by the cited authors quantified the critical gel point (Lu et al. 2014c). Notably, there was a relationship between the needed amount of cationic polymer and the specific amount of CNC employed, suggesting a stoichiometric interaction between the two. Such an interaction would be analogous to certain nanoparticle-based systems used as drainage and retention aids during papermaking (Andersson and Lindgren 1996; Hubbe 2005). Lenze et al. (2016) showed that sulfate-stabilized CNC can be used in place of the usual colloidal silica often employed by papermakers, and that similar effects on drainage and retention could be achieved. The observed effects depended on the ratio of amounts of cationic polyelectrolyte and negatively charged nanocellulose.
Ahola et al. (2008) obtained evidence that the interaction of a highly charged cationic polyelectrolyte, poly-(diallyldimethylammonium chloride) (poly-DADMAC) may cause dehydration of the cellulosic surfaces. This assertion was backed up by dissipation analysis, using a quartz crystal microbalance system, in combination with surface plasmon resonance tests. The effects were consistent with the earlier work of Ström and Kunnas (1991), who observed decreased water absorption values following treatment of cellulosic fibers with cationic polymers.
Earlier work involving ordinary-sized cellulose fibers can provide further insight regarding the interaction of cationic polymers with cellulosic surfaces. Swerin (1998) carried out rheological tests of bleached kraft fibers suspensions, showing the effects of flocculation by cationic acrylamide copolymers of very high mass. Critical strain and modulus values were greatly increased by the polymer treatment. The authors accounted for their results by proposing that the polyelectrolyte bridging induced more points of connection within the flocculated fiber structure. It is possible that such a model would not be as suitable in the case of nanocellulose – especially CNC – because it depends on there being a large difference in size between the macromolecule and the cellulose entities.
In the presence of anionic polyelectrolytes, several studies have shown strong gelation upon addition of calcium ions (Agoda-Tandjawa et al. 2012; Jowkarderis and van de Ven 2015; Cao et al. 2016). Such effects are consistent with a bridging interaction, in which the divalent ions mediate between pairs of carboxylate functions (Siew et al. 2005; Bulo et al. 2007). The general principle is shown in Fig. 24. At the same time, it is known that the divalent ions will tend to decrease the molecular extension of negatively charged polymer chains, which sometimes results in a decrease in viscosity (Yang and Zhu 2007).
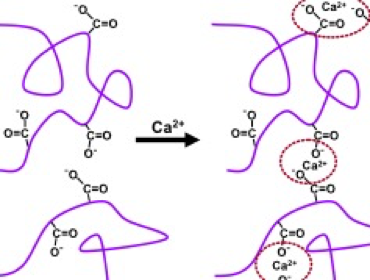
Fig. 24. Hypothetical mechanism by which divalent ions can greatly increase viscous effects within dispersed systems that contain negatively charged polyelectrolytes. Reversible connecting points in the structure are shown with dotted ellipses.
LIQUID CRYSTAL RHEOLOGICAL EFFECTS
Because of their unique optical effects, nanocellulose-based liquid crystals can be regarded as a unique system within which to evaluate various concepts already discussed in this article. Nanocellulose crystals, depending on their aspect length, aspect ratio, uniformity, and the forces between them, can become mutually oriented spontaneously (Marchessault et al. 1961; Dong and Gray 1997). Marchessault et al. (1961) were the first to report a strong dependency of crystal length on such phenomena in the case of CNC.
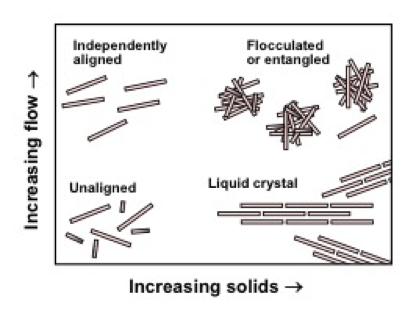
Fig. 25. Some generalized states of organization that have been commonly reported for nanocellulose suspensions, depending on solids level and hydrodynamic shear
As noted by Bercea and Navard (2000), often it is necessary for a certain solids content to be reached before the alignment will take place in the absence of flow. The cited authors showed that there can be a transition from “isotropic at rest” (disoriented) to “anisotropic at rest” (oriented) as a function of increasing concentration of nanocellulose in the suspension. They noted that both the development and dissipation of liquid crystal behavior tended to be more rapid in comparison with polymer solutions having liquid crystal behavior. Echeverria et al. (2015) found that application of high shear transformed CNC liquid crystal suspensions to flow-aligned nematic structure. Figure 25 provides a schematic representation of different states of organization, as a function of solids content and flow, as has been generally described in the literature.
Ordering phenomena observed in sufficiently concentrated or sheared suspensions of nanocrystals include the development of chiral nematic phases (Dong and Gray 1997; Beck et al. 2005). The word “chiral” refers to the presence of a twisting effect, such that there may be a systematic deviation in alignment as a function of distance from an arbitrarily defined reference point. It has been proposed that the detailed twisted shape of cellulose nanocrystals (Majoinen et al. 2016) may result in slight systematic shifts in the alignment of neighboring particles, giving rise to the chiral nature of the liquid crystal suspension (Dufresne 2012). Nematic means that the crystals are oriented parallel to each other but not necessarily organized into coherent planes. Some suspensions of CNC will display iridescence, in which different regions of the mixture will have different appearance, e.g. an undulating rainbow-like pattern. Liu et al. (2014) proposed a mechanism, involving Bragg diffraction effects of regularly spaced layers, to account for such colors. When viewed with polarized light, effects known as birefringence may be detected; such effects can be attributed to the fact that well-aligned cellulose molecules or crystals have different refractive index values depending on the direction of the light (Cranston and Gray 2008). The periodicity in the optical pattern gives evidence of the distances over which the particle alignment remains coherent. Dong and Gray (1997) observed sharp boundaries of the crystalline domains in CNC suspensions. Araki and Kuga (2001) found that very low levels of electrolyte (e.g. below 1 mM NaCl) promoted phase separation of charge-stabilized CNC suspensions and the formation of chiral nematic phases.
The nature of liquid crystal effects in CNC suspensions can be understood by observing how their optical and rheological manifestations can be disrupted in various systematic ways. For instance Dong and Gray (1997) added a series of different monomeric cations and noted that the critical concentration for the development of chiral nematic features was in the order H+ < Na+ < K+ < Cs+. The cited authors proposed that their findings provide evidence of a balancing between attractive forces (e.g. London dispersion) and electrostatic repulsion, in such a way as to hold the particles in mutual alignment. In terms of Fig. 17, such alignment is expected to involve an arrangement and orientation of CNCs so that the distances correspond to a secondary minimum of interaction free energy. Shafiei-Sabet et al. (2013) reported that the transition from isotropic to chiral-nematic ordering depended on the density of sulfate groups on the CNC surfaces. Higher charge corresponded to higher solids at the transition. However, since the different batches of CNC may have differed in other respects, such as particle width, other explanations are possible. Dong et al. (1996) showed that the solids level corresponding to the transition from an isotropic (disordered) to chiral nematic arrangement was shifted to higher values by the addition of electrolytes, which is consistent with the decreasing of double layer thickness.
Liquid crystal phenomena can be detected by comparing the results of certain rheometric tests. Cox and Merz (1958) had observed, in the case of ordinary suspensions of particles, that there is a generally a similarity between the viscosities measured by simple shear tests and those that they calculated from the stress-strain relationships during oscillatory rheometric tests. Thus, for typical suspensions, it is possible to estimate the shear modulus based on steady-state flow data (Doraiswamy et al. 1991). Deviations from this so-called “Cox-Merz rule” have been widely reported in the case of cellulosic nanocrystal suspensions (Lu et al. 2014a; Wu et al. 2014; Ahn and Song 2016; Qiao et al. 2016) and nanofibrils (Nazari et al. 2016). Lu et al. (2014a) studied systems in which the CNC suspensions showed temporary shear-induced birefringence, which disappeared in the absence of flow. By contrast, Noroozi et al. (2014) observed a cholesteric pattern at low shear rates below the yield point of suspension and alignment effects when the shear rates were increased. A cholesteric liquid crystal can be defined as a layered structure in which particles within a given layer have a common alignment, but in which the alignment differs between adjacent layers. By contrast, for high aspect ratio long NFC fibrils chiral alignment due to the low shear rate twisting of fibrils disappears once the shear rate approaches the yield point (Dimic-Misic et al. 2017a,b).
Elastic features of suspensions were noted by Doraiswamy et al. (1991). It was observed that flow-induced ordering within a suspension is able to store a certain amount of energy, which is released when the stress on the system is relaxed. One likely explanation is that the stored energy is associated with repulsive forces between the surfaces; according to that concept, the cessation of flow then allows the particles to move away from positions that were energetically unfavorable in terms of colloidal forces. A second explanation for the stored energy is that it may be due to an entropic effect. The degree of order within the system, under the influence of flow, will spontaneously become somewhat less ordered when then flow field is no longer being applied. Orts et al. (1995) used small angle neutron scattering (SANS) to find evidence of the rate of such relaxation in the case of cellulosic microfibril suspensions. It was found that the degree of alignment tended to increase with increasing shear rate, but the greatest alignment was observable about one minute after the cessation of shear. Such behavior is consistent with a process of mutual alignment among neighboring CNCs due to their electrostatic repulsions. However, such ordering does not necessarily preserve itself in a strict manner over long distances or periods of time. Follow-up work showed that the CNC could also be aligned by a magnetic field (Orts et al. 1998). The relaxation rate can be strongly affected by particle length and aspect ratio (Pääkkönen et al. 2016). Ureña-Benavides et al. (2011) studied the rheology of systems simultaneously containing both isotropic and liquid crystalline regions; the interface between such regions appeared to affect the elastic phenomena. Echeverria et al. (2016) showed that the addition of CNC affected the liquid-crystalline behavior of solutions of the nonionic polymer hydroxypropylcellulose (HPC). At low shear rates, CNC tended to restrict the mobility of the adjacent polymer molecules.
Some studies have indicated that liquid crystal features that are observed in certain suspensions of CNC also can persist when the material is formed into a film with the removal of water (Revol et al. 1992; Liu et al. 2011). Liu et al. (2011) noted a sufficient degree of preserved alignment such as to impart color to the resulting films after drying. Revol et al. (1992) used the term “regularly twisted fibrillar layers” in order to emphasize the slightly twisted nature that cellulose can adopt in suspension. Elazzouzi-Hafraoui et al. (2008) discussed whether such twisting corresponds to a slightly twisted character that cellulose may develop during its biosynthesis and formation into fibrils and crystallites, or whether slight twisting might be an artifact of later processes associated with isolation of the crystallites.
PROCESSING OF AQUEOUS SUSPENSIONS OF NANOCELLULOSE
Though technology related to nanocellulose has received a great deal of attention from researchers, there are many barriers to its industrial application, including the complexity of rheological phenomena. Further difficulties in implementation might be related to the challenges inherent in attempting to reproduce exactly the same nanocellulose characteristics in successive production runs. This section will consider progress in applying what has been learned about nanocellulose rheology in current or potential application areas.
Flow Modification
Drilling fluids, which are employed during the process of extracting petroleum from underground locations, need to have a combination of rheological and filtration properties. Li et al. (2016) showed that CNCs were able to improve the rheological characteristics of drilling fluids that also contained montmorillonite and a material that they called poly-anionic cellulose. The latter consisted of cellulosic fibers having a high density of carboxylate groups at their surfaces. The cellulosic fibers appeared to serve as a filter aid, whereas the CNC appeared to function as a thickener. Li et al. (2015b) showed that CNCs were preferable to MFCs because of their smaller dimensions, higher stability in aqueous suspensions, higher tolerance of high temperatures, and lesser shear-thinning tendency. The higher surface charge density of the studied CNCs was also viewed as being advantageous for that application.
Cellulose-based nanomaterials also have been evaluated for application as thickeners in food (Okiyama et al. 1993; Jonas and Farah 1998; Lowys et al. 2001; Mihranyan et al. 2007; Jia et al. 2014; Feng et al. 2015; Lin et al. 2015; Gomez et al. 2016; Qiao et al. 2016). Many of the cited studies dealt with bacterial cellulose, which has been “generally recognized as safe” for food applications (Shi et al. 2013). The water-holding ability of BC gels, as well as their contribution to providing a smooth texture, has been noted as a desirable property for some food products by the US Food and Drug Administration (Okiyama et al. 1993). BC also appears to act as a stabilizer for emulsified food products (Gomez et al. 2016), which is consistent with its tendency to form gel structures. Lowys et al. (2001) showed that the performance of BC as a thickener could be enhanced by the addition of NaCl. The effect was attributed to net forces of adhesion between the cellulose at points of contact within the gel structure.
Coating Formulation
In aqueous coating formulations for paper products, NFC appears to provide favorable attributes of water retention and thickening (Dimic-Misic et al. 2013a; Gruneberger et al. 2014; Zhou et al. 2014; Rautkoski et al. 2015; Salo et al. 2015; Nazari and Bousfield 2016; Xu et al. 2016). Dimic-Misic et al. (2013a, 2014) reported that NFC tends to act as both viscosity enhancer and water-binding agent, whereas conventional thickeners used in coating formulation, such as CMC, appear to serve more as viscosity enhancers. Lower surface charge MFC fibrils that are less water binding can be used as a viscosity enhancer and dispersant for pigments. Thus, adjustments in the density of the surface charge of NFC and MFC can be used to tune the rheological and water-retaining properties of coating colors.
The rate of immobilization of a coating formulation can affect the resulting smoothness of the coating, as well as influencing whether or not there is premature drying of coating material. Too rapid immobilization can give rise to the formation of stalagmites on the coating blade, which can cause surface imperfections such as scratches and streaks (Dimic-Misic et al. 2013a). Dimic-Misic et al. (2014) and Salo et al. (2015) proposed that flocculation interactions of NFC in a coating formulation may help prevent sagging of a just-applied coating layer on paper, thus helping to maintain a smooth surface. Flocculation can also lead to increased coating bulk, which aids in the coverage of low brightness substrates. Dimic-Misic et al. (2013b) introduced an alternative method for assessment of immobilization, and they reported that the mechanism was governed by the swelling of cellulosic fibrils that affect the gel-like properties of coatings and filler- nanocellulose complex suspensions in general. Pääkönen et al. (2016) referred to such water retention within NFC as “network swelling”. According to Salo et al. (2015), not only was NFC able to reduce sagging effects after application of coating formulations to paper, but also such addition did not adversely affect the leveling of the coating surface, which would be an expected consequence of too-rapid immobilization.
For a paper coating formulation, one of the basic requirements of the mixture is to tolerate a wide range of shear rate during a coating process without much change in its properties. This wide range of shear rate includes low to moderate rates of shear (0.1 to 1000 s-1) during pumping and mixing, high-shear (1000 to 100,000 s-1) during application, and ultra-high shear (100,000 to 2000,000 s-1) in the course of final rod or blade metering process (Roper III 1996). As discussed above, nanocellulose in its unmodified form exhibits very high sensitivity for shear stress and tends to shear thinning behavior. Kumar et al. (2016a) were able to do a controlled continuous application of NFC with a pilot scale slit coater at a low coating speed (1 to 30 m/min). Kumar et al. (2017) developed a specialized slot-die, through which a nanocellulose suspension can be applied to paper. With this device, the slot through which the suspension is delivered is held against a moving paper web on a backing roll, and the slot acts as the metering element.
Printing and 3D Printing Formulation
Nanocellulose also has been considered as a component in formulations for three-dimensional printing, which can be defined as a way to systematically build up planned structures by accurate X-Y placement of fusable droplets, in multiple layers, on a substrate (Shao et al. 2015). The cited authors evaluated the rheological properties of 3D printing formulations that contained MFC and described its functions in thickening and structure building.
As noted by Siqueira et al. (2017), an ideal ink material for 3D printing behaves as a fluid during its passage through print nozzles, but it acquires solid-like characteristics soon after its application on a surface. In principle, such behavior is consistent with the shear-thinning and thixotropic attributes of nanocellulose systems, as reported by many authors. Siqueira et al. (2017) showed in addition that ink-jet printing tends to align CNCs in the print direction due to hydrodynamic shear during printing.
Tang et al. (2016) observed that NFC produced from TEMPO-oxidized bleached hardwood kraft pulp could be used with CdS quantum dots as a coating formulation for photoelectric inks. Related quantum dot materials for inkjet application already had been reported, but not with the inclusion of nanocellulose (Small et al. 2010).
One of the uncertainties regarding the role of nanocellulose during 3D printing applications is whether or not the cellulose fibrils will be able to inter-twine with each other in such a way as to reinforce the boundaries between material that had been in separately applied droplets. In principle, such inter-twining would be important for achieving high strength and avoiding fracture of the formed structures. This is an issue that might be considered in future research.
Smart Effects
The word “smart” can be used to define a system that can be changed markedly and predictably in its behavior through the adjustment of a selected variable, such as temperature or pH. Such systems are of great theoretical interest for nanocellulose-containing suspensions, and they also have potential to be useful.
Thermo-responsive effects of nanocellulose suspensions have been reported by Zoppe et al. (2011) and by Azzam et al. (2016). Zoppe et al. (2011) achieved such effects by grafting of poly(N-isopropylacrylamide) chains onto CNC surfaces. A sharp drop in suspension viscosity was observed when the temperature was increased in the vicinity of the lower critical solution temperature of the polymer. The effects were consistent with aggregation of the CNC particles, a process that was induced by conformational changes in the grafted chains. Azzam et al. (2016) subjected CNC to TEMPO-mediated oxidation, and then formed the amide linkage to thermosensitive Jeffamine polyetheramine M2005 chains. The aggregation behavior first of all could be varied by adjusting the ionic strength and pH. A transition from liquid-like to gel-like properties was triggered reversibly by temperature increases in the range of about 18 to 34 °C. Such effects may have potential medical applications (Scheuble et al. 2016). Though none of these effects can be regarded as unexpected for the polymer types mentioned, these are apparently the first reports of grafted CNC suspensions showing such behavior.
A unique CO2-sensitive system was reported by Wang et al. (2015). CNC was reacted with 1-(3-aminopropyl)imidazole (APIm) by means of a diimidazole-mediated coupling. As a result, the CNC surfaces were populated with primary amine functions. When N2 was bubbled through the suspension of modified CNC, the suspension agglomerated to form a gel. Subsequent sparging of CO2 through the suspension redispersed the particles as a low-viscosity mixture in a reproducible cycle. Since CO2 is known to form carbonic acid in solution, and since sparging with nitrogen gas tends to remove CO2 from the system, the observed effects are consistent with the expected changes in pH.
Unusual gelation conditions were reported by Agoda-Tandjawa et al. 2012 for suspensions containing MFC and pectin. Combinations of both sodium and calcium ions were observed to be effective for gelation of the mixture. It appears that the role of the sodium ion is to suppress the double layer extent and that the calcium then is more able to function as a bridging and gelling agent.
Effects of Drying of Nanocellulose on Redispersion and Rheology
Consequences of ordinary drying
Changes in the properties of nanocellulose as a consequence of drying have been regarded as an important barrier to certain industrial applications (Okiyama et al. 1993; Peng et al. 2012). Researchers have observed great losses in swelling ability or contributions to viscosity when NFC and related materials are dried (Zepic et al. 2014). In the case of CNC, Khoshkava and Kamal (2014) showed that drying by various means yielded dense agglomerates of the nanocellulose particles. In related work, Kekalainen et al. (2014a) showed that the drying of kraft pulp fibers before high-shear homogenization impeded the preparation of NFC; the resulting NFC tended to have lower water retention. Such results are consistent with the coalescence of adjacent nanofibrils into larger units in the course of drying. Such coalescence may involve a crystal healing mechanism at the interfaces (Pönni et al. 2012). Xia et al. (2015) observed that the release of water from nanocellulose hydrogels resulted in permanent changes associated with such hydrogen bonding.
Alternative drying procedures
Ordinary drying of delignified cellulosic material is known to involve semi-permanent closure of mesopores in the cell walls of fibers (Stone and Scallan 1966; Weise 1998; Hubbe et al. 2007), and also the development of organized patterns of hydrogen bonding similar to crystallization at the boundary between cellulose phases (Pönni et al. 2012). The loss of ability of cellulosic material to take up as much water again after it has been dried has been called hornification (Weise 1998). Highly fibrillated cellulose appears to be very susceptible to such effects (Eyholzer et al. 2010; Naderi et al. 2015b). The susceptibility to hornification seems consistent with the relatively high purity of cellulose within many NFC or MFC samples, the fact that cellulose molecules and fibrils often are already well aligned in such materials, and also due to the flexibility and conformability of the cellulosic fibrillar strands.
In an effort to minimize the adverse effects of drying on the ability of NFC and related products to function later as viscosity modifiers, researchers have compared the effects of alternative drying strategies (Khoshkava and Kamal 2014; Zepic et al. 2014; Feng et al. 2015). The idea has been that there may be a way to decrease the degree of hydrogen bond formation between adjacent cellulose entities, thereby facilitating full rewetting, swelling, and contributions to viscosity when the material is placed back in water. Spray drying is often regarded as a practical way to prepare storage-stable, shippable forms of nanocellulose (Amin et al. 2014). The cited authors found that acid treatment decreased the viscosity contribution of BC to a greater extent than spray drying of the material. Zepic et al. (2014) observed that both air drying and oven drying resulted in an interlaced network, consistent with the formation of strong bonding among cellulose fibrils.
Freeze drying typically is carried out under a vacuum, such that net evaporation takes place well below the ambient boiling point of water. The heat of phase change results in a decrease in temperature, and conditions can be adjusted such that much of the process takes place below the freezing point of water. It has been hypothesized that drying under such conditions might avoid the possibility of some aspects of hornification, such that one might expect there to be less effect on the cellulosic material’s ability to contribute to viscosity of aqueous suspensions. Experimental results, however, tell another story. For instance, Agoda-Tandjawa et al. (2010) observed strong decreases in viscosity when comparing suspensions of MFC that had been freeze-dried or never dried. Storage modulus values were decreased to about half the values that would have been achieved with never-dried MFC. Ordinary freezing of the whole suspensions preserved the viscosities of such mixtures, indicating that the observed changes were attributable to drying rather than to the freezing. Zepic et al. (2014) observed that freeze-drying, when compared to ordinary drying, considerably reduced the extent of aggregation and resulted in two classes of solid material – coarse and fine powder fractions. The freeze-dried powders formed more stable suspensions than the spray-dried powders when placed into water. Likewise, Khoshkava and Kamal (2014) observed better dispersion of freeze-dried CNC in comparison to spray-dried CNC. However, they also found that freeze drying led to aggregation, leading to dense particles. They attributed the aggregation to the growth of ice crystals, which tended to force the cellulosic material together. Related findings were reported by Jiang and Hsieh (2014).
Xu et al. (2017) showed recently that ordinary freezing of CNC suspensions can have different effects on the arrangement of particles, depending on the salt concentration. They started by considering charge-stabilized CNC suspensions at sufficiently high solids such that the particles tended to be aligned (anisotropic). Addition of enough salt to thin the double layers, but not to destabilize the suspension, caused the particles to become disoriented. Higher salt, enough to bring about sticking collisions among the particles, caused gelation. But freezing of the three systems led, respectively to smooth aligned layers (no salt), rough layers of clusters (intermediate salt), and very thick layers of networks (high salt), respectively.
A few researchers have considered mechanical processing in an attempt to re-hydrate nanocellulose material after its drying and the loss of swelling ability. Ambrosio-Martin et al. (2015) found that ball milling was effective for breaking up aggregates of nanocellulose that had been freeze-dried.
Chemical Treatments to Avoid Adverse Effects of Drying
Various chemical-based approaches have been considered as means to avoid the above-mentioned adverse consequences of drying nanocellulose. Again, the most successful of these approaches appear to have been aimed at interfering with the formation of organized hydrogen bonding between cellulosic surfaces during the drying process.
Hydrophilic polymer adsorption to minimize hornification
Adoda-Tandjawa et al. (2010) cite studies in which water-soluble natural polymers were added to cellulose suspensions before drying in order to minimize the loss of swelling ability. For instance, Lowys et al. (2001) reported that the ability of MFC to contribute to storage modulus of suspensions could be preserved by adding 5% by dry mass or more of various carboxymethylcellulose (CMC) products. The best results were achieved when using CMC having a relatively high degree of substitution, e.g. 1.2 or 2.0. Butchosa and Zhou (2014) showed that addition of as little as 2.3% of CMC solution (degree of substitution 0.90) in terms of dry mass to NFC before drying allowed for good redispersibility, and the viscosity properties were near to those observed prior to drying. Naderi et al. (2015b) reported similarly favorable results when preparing NFC in the presence of relatively high-negative-charge CMC before drying. One set of samples (prepared by impeller agitation) achieved equal viscosity performance when comparing NFC that had been treated with CMC with never-dried NFC. In the case of NFC that had been prepared with high-shear mixing, some loss in viscosity was observed in the drying step. It is worth noting, in the cited work, that the CMC functioned not only as a way to avoid the negative consequences of drying, but it also greatly facilitated the initial fibrillation. Kim and Lee (2010) evaluated various other hydrophilic polymers for the pretreatment of drug nanosuspensions that contained hydroxypropylcellulose; the addition of 0.5% by mass of carrageenan was sufficient to achieve good redispersibility. Ben Azouz et al. (2012) likewise reported favorable results when pretreating CNC suspensions with poly-(ethyleneoxide) (PEO) before drying. Improved redispersibility was observed. Using a different approach to achieve similar objectives, Eyholzer et al. (2010) were able to produce redispersible NFC by carboxymethylation of the surfaces before drying.
NaCl addition before drying
Missoum et al. (2012b) reported favorable results when combining the approaches of NaCl treatment, followed by freeze drying. This strategy was most successful when carried out at a pH of 8 (pH >> pKa), which is consistent with deprotonation of the carboxyl groups of the NFC. The cited authors proposed that the salt ions associate with the polar –OH groups of the cellulose, thereby impeding the development of hydrogen bonding between the cellulose surfaces during drying. If and when it is decided to use salt to facilitate the drying and subsequent rewetting and use of nanocellulose as a viscosity aid, one needs to take into account the fact that residual NaCl or KCl in the mixture can be expected to contribute to gelation of nanocellulose suspensions (Lowys et al. 2001; Zhang et al. 2015).
Drying after dispersion in non-aqueous solvent
Araki and Arita (2017) pioneered the dispersion of nanocellulose in non-aqueous solvents as a means of preparing easily water-dispersible suspensions. CNC was prepared by hydrolysis of cotton, using concentrated HCl. When dried from water, such CNC cannot be readily redispersed. By contrast, the cited authors achieved high redispersibility when the mixtures were dispersed in such solvents as toluene or cyclohexane prior to drying. Solvents of relatively high dielectric constant and polarity yielded dried cellulosic membranes that could not be redispersed.
CLOSING COMMENTS
It is clear from publications considered in this review that a great deal of progress has been achieved in understanding rheological phenomena related to aqueous suspensions of nanocellulose. Though many aspects of such rheology can be addressed in terms of well-known concepts and models, it appears that some of the most interesting issues involve observations that fall outside of well-established concepts and models. The highly elongated nature of NFC and BC materials in suspension favors irreversible mechanisms, such as entanglement and non-repairable rupture of network structures. Further progress will likely involve yet closer attention to the details of nanocellulose structure and its modifications. Future work may focus on the detailed structure of floc fragments obtained after the breakage of nanocellulose gels that have been stressed or strained beyond their reversible limits.
Another area of focus that may be fruitful for future research is the analysis of interactive forces between cellulosic surfaces. Such studies have the potential to improve scientists’ understanding of gel structures that are formed by nanocellulose particles, and how they can be modified or controlled by chemical treatments or by adjustment of aqueous conditions. Progress in electron-microscopic examination and atomic force microscopy of cellulose nanofibrils segments can be used as the basis for constructing mathematical models, making it possible to estimate component forces, such as van der Waals and electrostatic components of force, as well as the effects of intervening polyelectrolytes.
The present state of knowledge pertaining to aqueous nanocellulose suspensions appears to be sufficient to rationalize, but not necessarily to predict, rheological behaviors based on morphological and surface-chemical specifications. This state of affairs might be attributed to situations in which sharply different rheological behavior may arise depending on whether or not cellulose-based structures within a gel or suspension are contiguous – having a continuous network of cellulosic particles incorporating all of the volume in the test apparatus. Chemical treatments often can lead to opposite effects on viscosity, depending on whether the excluded volume effects (due to double-layer thickness) or coagulation effects (due to sufficient decreases in energy barriers to allow contacts between surfaces) happen to be dominant. A possible way to resolve this state of affairs may require widespread production of highly uniform, individually dispersed fibril products, i.e. CNF according to the nomenclature used in this review article. Whether or not such nanocellulose is ideal for a given application, at least the physical and chemical factors giving rise to rheological phenomena would be easier to predict and control.
Though hydrogels prepared with just nanocellulose and water may have applications in absorbency, food, and medicine, among others, one can envision many further applications in which the aqueous formulation includes not only nanocellulose but also various water-soluble polymers or emulsions. Many of the related issues can be expected to go beyond the scope of what has been considered in the present article. It is our hope that the present consideration of aqueous suspensions of nanocellulose can provide clues about what to expect when viscous effects of matrix materials such as polyelectrolytes or melts may play a dominant role.
Another take-away message from the publications considered in this review is that nanocellulose products appear to have a promising future for the control of rheological properties of formulations in food, pharmaceuticals, and various industrial applications. The structural complexity of the cellulosic material and challenges in defining and reproducing its characteristics from batch to batch seem likely to slow down adoption of nanocellulose in such applications, relative to conventional polymeric thickening agents. However, the people-friendly and eco-friendly nature of the cellulose source material can be regarded as a motivating factor for the eventual adoption of nanocellulose in many such formulations. The inherent fibrillar nature and chemical stability of cellulose are likely to be advantageous relative to the performance of many coatings, films, and composite structures that could be formed with nanocellulose. It is recommended that there should be further efforts to understand the flow behavior of such systems as a means to support future research progress and industrial innovation in these areas.
ACKNOWLEDGMENTS
The authors are grateful for the following sources of support for this work: The Buckman endowment, which supports the work of Dr. Hubbe; the Department of Forest Biomaterials and College of Natural Resources, which supports Dr. Pal; and The NCSU Provost’s Fellowship Award, which supports the work of Preeti Tyagi. The authors wish to thank the following volunteers who recommended numerous corrections, clarifications, and important missing information: Robin Zuluaga of Univ Pontificia Bolivariana, Fac. Ingn. Agroind., Medellin, Colombia; Justin Zoppe of Ecole Polytech. Fed. Lausanne, Inst. Mat., Lausanne, Switzerland; Yaman Boluk of the University of Alberta, Dept. Civil & Environm. Engn., Edmonton, Alberta, Canada; and Jun Araki of Shinshu University, Faculty of Textile Science & Technology, Ueda, Nagano, Japan.
REFERENCES CITED
Agoda-Tandjawa, G., Durand, S., Berot, S., Blassel, C., Gaillard, C., Garnier, C., and Doublier, J. L. (2010). “Rheological characterization of microfibrillated cellulose suspensions after freezing,” Carbohyd. Polym. 80(3), 677-686. DOI: 10.1016/j.carbpol.2009.11.045
Agoda-Tandjawa, G., Durand, S., Gaillard, C., Garnier, C., and Doublier, J. L. (2012). “Rheological behaviour and microstructure of microfibrillated cellulose suspensions/low-methoxyl pectin mixed systems. Effect of calcium ions,” Carbohydr. Polym. 87(2), 1045-1057. DOI: 10.1016/j.carbpol.2011.08.021
Ahn, S. Y., and Song, Y. S. (2016). “Viscoelastic characteristics of all cellulose suspension and nanocomposite,” Carbohydr. Polym. 151, 119-129. DOI: 10.1016/j.carbpol.2016.05.059
Ahola, S., Myllytie, P., Österberg, M., Teerinen, T., and Laine, J. (2008). “Effect of polymer adsorption on cellulose nanofibril water binding capacity and aggregation,” BioResources 3(4), 1315-1328. DOI: 10.15376/biores.3.4.1315-1328
Ambrosio-Martin, J., Lopez-Rubio, A., Fabra, M. J., Gorrasi, G., Pantani, R., and Lagaron, J. M. (2015). “Assessment of ball milling methodology to develop polylactide-bacterial cellulose nanocrystals nanocomposites,” J. Appl. Polym. Sci. 132(10), Article no. 41605. DOI: 10.1002/app.41605
Amin, M. C. I. M., Abadi, A. G., and Katas, H. (2014). “Purification, characterization and comparative studies of spray-dried bacterial cellulose microparticles,” Carbohyd. Polymers 99, 180-189. DOI: 10.1016/j.carbpol.2013.08.041
Anderson, S. R., Esposito, D., Gillette, W., Zhu, J. Y., Baxa, U., and McNeil, S. E. (2014). “Enzymatic preparation of nanocrystalline and microcrystalline cellulose,” TAPPI J. 13(5), 35-42.
Andersson, K., and Lindgren, E. (1996). “Important properties of colloidal silica in microparticulate systems,” Nordic Pulp Paper Res. J. 11(1), 15-21, 57.
Araki, J. (2013). “Electrostatic or steric? – Preparations and characterizations of well-dispersed systems containing rod-like nanowhiskers of crystalline polysaccharides,” Soft Matter 9(16), 4125-4141. DOI: 10.1039/c3sm27514k
Araki, J., and Arita, T. (2017). “Production of ultrafine dry powders of surface-intact and unmodified cellulose nanowhiskers via homogenization in nonpolar organic solvents,” Chemistry Letters 46(9), 1438-1441. DOI: 10.1246/cl.170588
Araki, J., and Kuga, S. (2001). “Effect of trace electrolyte on liquid crystal type of cellulose microcrystals,” Langmuir 17, 4493-4496.
Araki, J., Wada, M., and Kuga, S. (2001). “Steric stabilization of cellulose microcrystal suspension by poly(ethylene glycol) grafting,” Langmuir 17(1), 21-27. DOI: 10.1021/la001070m
Araki, J., Wada, M., Kuga, S., and Okano, T. (1998). “Flow properties of microcrystalline cellulose suspension prepared by acid treatment of native cellulose,” Colloids Surf. 142(1), 75-82. DOI: 10.1016/S0927-7757(98)00404-X
Araki, J., Wada, M., Kuga, S., and Okano, T. (2000). “Influence of surface charge on viscosity anomaly of microcrystalline cellulose suspensions,” in: Hydrocolloids, Pt 1: Physical Chemistry and Industrial Application of Gels, Polysaccharides, and Proteins, K. Nishinari (ed.), Osaka-City-University International Symposium 98/4th International Conference on Hydrocolloids, pp. 283-288. DOI: 10.1016/B978-044450178-3/50035-4
Araki, J., Wada, M., Kuga, S., and Okano, T. (1999). “Influence of surface charge on viscosity behavior of cellulose microcrystal suspension,” J. Wood Sci. 45, 258-261. DOI: 10.1007/BF01177736
Arola, S., Malho, J. M., Laaksonen, P., Lille, M., and Linder, M. B. (2013). “The role of hemicellulose in nanofibrillated cellulose networks,” Soft Matter 9(4), 1319-1326. DOI: 10.1039/c2sm26932e
Azzam, F., Siqueira, E., Fort, S., Hassaini, R., Pignon, F., Travelet, C., Putaux, J. L., and Jean, B. (2016). “Tunable aggregation and gelation of thermoresponsive suspensions of polymer-grafted cellulose nanocrystals,” Biomacromol. 17(6), 2112-2119. DOI: 10.1021/acs.biomac.6b00344
Baheti, V., and Militky, J. (2013). “Reinforcement of wet milled jute nano/micro particles in polyvinyl alcohol films,” Fibers Polymers 14(1), 133-137. DOI: 10.1007/s12221-013-0133-4
Barnes, H. A. (1995). “A review of the slip (wall depletion) of polymer solutions, emulsions and particle suspensions in viscometers: Its cause, character, and cure,” J. Non Newton. Fluid Mech. 56, 221-251. DOI: 10.1016/0377-0257(94)01282-M
Barnes, H. A. (1997). “Thixotropy—A review,” J. Non-Newtonian Fluid Mech. 70, 1-33. DOI: 10.1016/S0377-0257(97)00004-9
Beaumont, M., Rennhofer, H., Opietnik, M., Lichtenegger, H. C., Potthast, A., and Rosenau, T. (2016). “Nanostructured cellulose II gel consisting of spherical particles,” ACS Sustain. Chem. Eng. 4(8), 4424-4432. DOI: 10.1021/acssuschemeng.6b01036
Beck, S., and Bouchard, J. (2014). “Auto-catalyzed acidic desulfation of cellulose nanocrystals,” Nordic Pulp Paper Res. J. 29(1), 6-14. DOI: 10.3183/NPPRJ-2014-29-01-p006-014
Beck, S., and Bouchard, J. (2016). “Ionic strength control of sulfated cellulose nanocrystal suspension viscosity,” TAPPI J. 15(6), 363-372.
Beck, S., Methot, M., and Bouchard, J. (2015). “General procedure for determining cellulose nanocrystal sulfate half-ester content by conductometric titration,” Cellulose 22(1), 101-116. DOI: 10.1007/s10570-014-0513-y
Beck-Candanedo, S., Roman, M., and Gray, D. G. (2005). “Effect of reaction conditions on the properties and behavior of wood cellulose nanocrystal suspensions,” Biomacromolecules 6, 1048-1054. DOI: 10.1021/bm049300p
Beghello, L., and Lindström, T. (1998). “The influence of carboxymethylation on the fiber flocculation process,” Nordic Pulp Paper Res. J. 13(4), 269-273. 10.3183/NPPRJ-1998-13-04-p269-273
Ben Azouz, K., Ramires, E. C., Van den Fonteyne, W., El Kissi, N., and Dufresne, A. (2012). “Simple method for the melt extrusion of a cellulose nanocrystal reinforced hydrophobic polymer,” ACS Macro Lett. 1(1), 236-240. DOI: 10.1021/mz2001737
Benhamou, K., Dufresne, A., Magnin, A., Mortha, G., and Kaddami, H. (2014). “Control of size and viscoelastic properties of nanofibrillated cellulose from palm tree by varying the TEMPO-mediated oxidation time,” Carbohyd. Polym. 99, 74-83. DOI: 10.1016/j.carbpol.2013.08.032
Bennington, C. P. J., Kerekes, R. J., and Grace, J. R. (1990). “The yield stress of fibre suspensions,” Can. J. Chem. Eng. 68, 748-757. DOI: 10.1002/cjce.5450680503
Bercea, M., and Navard, P. (2000). “Shear dynamics of aqueous suspensions of cellulose whiskers,” Macromol. 33(16), 6011-6016. DOI: 10.1021/ma000417p
Bergenholtz, J., Brady, J. F., and Vicic, M. (2002). “The non-Newtonian rheology of dilute colloidal suspensions,” J. Fluid Mechanics 456, 239-275. DOI: 10.1017/S0022112001007583
Bergstrom, L., Stemme, S., Dahlfors, T., Arwin, H., and Odberg, L. (1999). “Spectroscopic ellipsometry characterisation and estimation of the Hamaker constant of cellulose,” Cellulose 6(1), 1-13. DOI: 10.1023/A:1009250111253
Berry, D. H., and Russel, W. B. (1987). “The rheology of dilute suspensions of slender rods in weak flows,” J. Fluid Mech. 180, 475-494. DOI: 10.1017/S0022112087001915
Besbes, I., Alila, S., and Boufi, S. (2011a). “Nanofibrillated cellulose from TEMPO-oxidized eucalyptus fibres: Effect of the carboxyl content,” Carbohydr. Polym. 84(3), 975-983. DOI: 10.1016/j.carbpol.2010.12.052
Besbes, I., Vilar, M. R., and Boufi, S. (2011b). “Nanofibrillated cellulose from alfa, eucalyptus and pine fibres: Preparation, characteristics and reinforcing potential,” Carbohyd. Polym. 86(3), 1198-1206. DOI: 10.1016/j.carbpol.2011.06.015
Bettaieb, F., Nechyporchuk, O., Khiari, R., Mhenni, M. F., Dufresne, A., and Belgacem, M. N. (2015). “Effect of the oxidation treatment on the production of cellulose nanofiber suspensions from Posidonia oceanica: The rheological aspect,” Carbohydr. Polym. 134, 664-672. DOI: 10.1016/j.carbpol.2015.07.091
Bhattacharya, M., Malinen, M. M., Lauren, P., Lou, Y. R., Kuisma, S. W., Kanninen, L., Lille, M., Corlu, A., GuGuen-Guillouzo, C., and Ikkala, O., et al. (2012). “Nanofibrillar cellulose hydrogel promotes three-dimensional liver cell culture,” J. Controlled Release 164(3), 291-298. DOI: 10.1016/j.jconrel.2012.06.039
Björkman, U. (2003a). “Break-up of suspended fibre networks,” Nordic Pulp Paper Res. J. 18(1), 32-37. DOI: 10.3183/NPPRJ-2003-18-01-p032-037
Björkman, U. (2003b). “Stress generation and transmission in suspended fibre networks,” Nordic Pulp Paper Res. J. 18(1), 38-43. DOI: 10.3183/NPPRJ-2003-18-01-p038-043
Björkman, U. (2006). “Floc dynamics in flowing fibre suspensions,” Nordic Pulp Paper Res. J. 20(2), 247-252. DOI: 10.3183/NPPRJ-2005-20-02-p247-252
Boluk, Y., Lahiji, R., Zhao, L. Y., and McDermott, M. T. (2011). “Suspension viscosities and shape parameter of cellulose nanocrystals (CNC),” Colloids Surf. A – Physicochem. Eng. Aspects 377, 297-303. DOI: 10.1016/j.colsurfa.2011.01.003
Boluk, Y., Zhao, L. Y., and Incani, V. (2012). “Dispersions of nanocrystalline cellulose in aqueous polymer solutions: Structure formation of colloidal rods,” Langmuir 28(14), 6114-6123. DOI: 10.1021/la2035449
Bottero, J-Y., and Fiessinger, F. (1989). “Aluminum chemistry in aqueous solution,” Nordic Pulp Paper Res. J. 4(2), 81-89. DOI: 10.3183/NPPRJ-1989-04-02-p081-089
Bounoua, S., Lemaire, E., Ferec, J., Ausias, G., and Kuzhir, P. (2016a). “Shear-thinning in concentrated rigid fiber suspensions: Aggregation induced by adhesive interactions,” J. Rheol. 60(6), 1279-1300. DOI: 10.1122/1.4965431
Bounoua, S., Lemaire, E., Férec, J., Ausias, G., Zubarev, A., and Kuzhir, P. (2016b). “Apparent yield stress in rigid fibre suspensions: The role of attractive colloidal interactions,” J. Fluid Mech. 802, 611-633. DOI: 10.1017/jfm.2016.475
Bowen, W. R., and Jenner, F (1995). “The calculation of dispersion forces for engineering applications,” Advan. Colloid Interface Sci. 56, 201-243. DOI: 10.1016/0001-8686(94)00233-3
Brenner, H. (1974). “Rheology of a dilute suspension of axisymmetric Brownian particles,” Int. J. Multiphase Flow 1, 195-341. DOI: 10.1016/0301-9322(74)90018-4
Brinkman, H. (1952). “The viscosity of concentrated suspensions and solutions,” J. Chem. Phys. 20, 571-571. DOI: 10.1063/1.1700493
Bulo, R. E., Donadio, D., Laio, A., Molnar, F., Rieger, J., and Parrinello, M. (2007). “ ‘Site binding’ of Ca2+ ions to polyacrylates in water: A molecular dynamics study of coiling and aggregation,” Macromol. 40(9), 3437-3442. DOI: 10.1021/ma062467l
Buscall, R. (2010). “Wall slip in dispersion rheometry,” J. Rheol. 54(6), 1177-1183. DOI: 10.1122/1.3495981
Butchosa, N., and Zhou, Q. (2014). “Water redispersible cellulose nanofibrils adsorbed with carboxymethyl cellulose,” Cellulose 21(6), 4349-4358. DOI: 10.1007/s10570-014-0452-7
Cao, Y. Z., Zavattieri, P., Youngblood, J., Moon, R., and Weiss, J. (2016). “The relationship between cellulose nanocrystal dispersion and strength,” Construc. Building Mater. 119, 71-79. DOI: 10.1016/j.conbuildmat.2016.03.077
Celzard, A., Fierro, V., and Kerekes, R. (2009). “Flocculation of cellulose fibers: New comparison of crowding factor with percolation and effective-medium theories,” Cellulose 16, 983-987. DOI: 10.1007/s10570-009-9314-0
Camarero Espinosa, S., Kuhnt, T., Foster, E. J., and Weder, C. (2013). “Isolation of thermally stable cellulose nanocrystals by phosphoric acid hydrolysis,” Biomacromol. 14(4), 1223-1230. DOI: 10.1021/bm400219u
Chaker, A., and Boufi, S. (2015). “Cationic nanofibrillar cellulose with high antibacterial properties,” Carbohydr. Polym. 131, 224-232. DOI: 10.1016/j.carbpol.2015.06.003
Chang, C. P., Wang, I. C., and Perng, Y. S. (2013). “Enhanced thermal behavior, mechanical properties and UV shielding of polylactic acid (PLA) composites reinforced with nanocrystalline cellulose and filled with nanosericite,” Cellulose Chem. Technol. 47(1-2), 111-123.
Chanzy, H. (1990). “Aspects of cellulose structure,” in: Cellulose Sources and Exploitation: Industrial Utilization, Biotechnology and Physico-chemical Properties,” J. F. Kennedy, B. L. Phillips, and P. A. Williams (eds.), Ellis Horwood Ser. in Polymer Sci. & Technol., Chichester, UK, pp. 3-12.
Charani, P. R., Dehghani-Firouzabadi, M., Afra, E., Blademo, A., Naderi, A., and Lindstrom, T. (2013a). “Production of microfibrillated cellulose from unbleached kraft pulp of Kenaf and Scotch pine and its effect on the properties of hardwood kraft: Microfibrillated cellulose paper,” Cellulose 20(5), 2559-2567. DOI: 10.1007/s10570-013-9998-z
Charani, P. R., Dehghani-Firouzabadi, M., Afra, E., and Shakeri, A. (2013b). “Rheological characterization of high concentrated MFC gel from kenaf unbleached pulp,” Cellulose 20(2), 727-740. DOI: 10.1007/s10570-013-9862-1
Chau, M., Sriskandha, S. E., Pichugin, D., Therien-Aubin, H., Nykypanchuk, D., Chauve, G., Methot, M., Bouchard, J., Gang, O., and Kumacheva, E. (2015). “Ion-mediated gelation of aqueous suspensions of cellulose nanocrystals,” Biomacromol. 16(8), 2455-2462. DOI: 10.1021/acs.biomac.5b00701
Chen, B., Tatsumi, D., and Matsumoto, T. (2002). “Floc structure and flow properties of pulp fiber suspensions,” Journal of the Society of Rheology Japan 30(1), 19-25. DOI: 10.1678/rheology.30.19
Chen, D. Z., and van de Ven, T. G. M. (2016). “Morphological changes of sterically stabilized nanocrystalline cellulose after periodate oxidation,” Cellulose 23(2), 1051-1059. DOI: 10.1007/s10570-016-0862-9
Chen, F., Hong, B., Guo, X., and Xue, G. X. (2013a). “Pretreatment of bamboo powder for cellulose nanocrystalline by sulfuric acid hydrolysis,” in: Current Trends in the Development of Industry, L. Yu, W. P. Guo, and J. He (eds.), Advan. Mater Res. 785-786, 346-353. DOI: 10.4028/www.scientific.net/AMR.785-786.346
Chen, G. Y., Yu, H. Y., Zhang, C. H., Zhou, Y., and Yao, J. M. (2016a). “A universal route for the simultaneous extraction and functionalization of cellulose nanocrystals from industrial and agricultural celluloses,” J. Nanoparticle Res. 18(2), article no. 48. DOI: 10.1007/s11051-016-3355-8
Chen, H., Ding, Y, and Tan, C. (2007). “Rheological behavior of nanofluids,” New J. Phys. 9(10), article no. 367. DOI: 10.1088/1367-2630/9/10/367
Chen, N. S., Zhu, J. Y., and Tong, Z. H. (2016b). “Fabrication of microfibrillated cellulose gel from waste pulp sludge via mild maceration combined with mechanical shearing,” Cellulose 32(4), 2573-2583. DOI: 10.1007/s10570-016-0959-1
Chen, P., Yu, H. P., Liu, Y. X., Chen, W. S., Wang, X. Q., and Ouyang, M. (2013b). “Concentration effects on the isolation and dynamic rheological behavior of cellulose nanofibers via ultrasonic processing,” Cellulose 20(1), 149-157. DOI: 10.1007/s10570-012-9829-7
Chen, X. Q., Deng, X. Y., Shen, W. H., and Jiang, L. L. (2012). “Controlled enzymolysis preparation of nanocrystalline cellulose from pretreated cotton fibers,” BioResources 7(3), 4237-4248. DOI: 10.15376/biores.7.3.4237-4248
Chen, Y., Xu, C. J., Huang, J., Wu, D. F., and Lv, Q. L. (2017). “Rheological properties of nanocrystalline cellulose suspensions,” Carbohyd. Polym. 157, 303-310. DOI: 10.1016/j.carbpol.2016.10.002
Chinesta, F., and Ausias, G. (eds.) (2016). Rheology of Non-spherical Particle Suspensions, ISTE Press – Elsevier.
Ching, Y. C., Ali, M. E., Abdullah, L. C., Choo, K. W., Kuan, Y. C., Julaihi, S. J., Chuah, C. H., and Liou, N. S. (2016). “Rheological properties of cellulose nanocrystal-embedded polymer composites: A review,” Cellulose 23(2), 1011-1030. DOI: 10.1007/s10570-016-0868-3
Chow, A. W., Sinton, S. W., Iwamiya, J. H., and Stephens, T. S. (1994). “Shear-induced particle migration in Couette and parallel-plate viscometers: NMR imaging and stress measurements,” Phys. Fluids 6, 2561-2576. DOI: 10.1063/1.868147
Claesson, P. M., Poptoshev, E., Blomberg, E., and Dedinaite, A. (2005). “Polyelectrolyte-mediated surface interactions,” Advan. Colloid Interface Sci. 114, 173-187. DOI: 10.1016/j.cis.2004.09.008
Colson, J., Bauer, W., Mayr, M., Fischer, W., and Gindl-Altmutter, W. (2016). “Morphology and rheology of cellulose nanofibrils derived from mixtures of pulp fibres and papermaking fines,” Cellulose 23(4), 2439-2448. DOI: 10.1007/s10570-016-0987-x
Cosgrove, D. J. (2014). “Re-constructing our models of cellulose and primary cell wall assembly,” Current Opin. Plat Biol. 22, 122-131. DOI: 10.1016/j.pbi.2014.11.001
Coussot, P., Nguyen, Q. D., Huynh, H. T., and Bonn, D. (2002). “Viscosity bifurcation in thixotropic, yielding fluids,” J. Rheol. 46(3), 573-589. DOI: 10.1122/1.1459447
Cox, W. P., and Merz, E. H. (1958). “Correlation of dynamic and steady flow viscosities,” J. Polym. Sci. 28, 619-622. DOI: 10.1002/pol.1958.1202811812
Cranston, E. D., and Gray, D. G. (2008). “Birefringence in spin-coated films containing cellulose nanocrystals,” Colloids Surf. A: Phsicochem. Eng. Aspects 325, 44-51. DOI: 10.1016/j.colsurfa.2008.04.042
Crawford, R. J., Edler, K. J., Lindhoud, S., Scott, J. L., and Unali, G. (2012). “Formation of shear thinning gels from partially oxidised cellulose nanofibrils,” Green Chem. 14(2), 300-303. DOI: 10.1039/c2gc16302k
Cui, H., and Grace, J. R. (2007). “Flow of pulp fibre suspension and slurries: A review,” Int. J. Multiphase Flow 33, 921-934. DOI: 10.1016/j.ijmultiphaseflow.2007.03.004
Dalpke, B., and Kerekes, R. J. (2005). “The influence of fibre properties on the apparent yield stress of flocculated pulp suspensions,” J. Pulp Paper Sci. 31(1), 39-43.
Damani, R., Powell, R. L., and Hagen, N. (1993). “Viscoelastic characterization of medium consistency pulp suspensions,” Can. J. Chem. Eng. 71, 676-684. DOI: 10.1002/cjce.5450710504
de Gennes, P. G. (1979). Scaling Concepts in Polymer Physics, Cornell Univ. Press, Ithaca.
de Kort, D. W., Veen, S. J., Van As, H., Bonn, D., Velikov, K. P., van Duynhoven, J. P. M. (2016). “Yielding and flow of cellulose microfibril dispersions in the presence of a charged polymer,” Soft Matter 12(21), 4739-4744. DOI: 10.1039/c5sm02869h
Delgado-Aguilar, Gonzalez, I., Tarres, Q., Alcala, M., Pelach, M. A., and Mutje, P. (2015). “Approaching a low-cost production of cellulose nanofibers for papermaking applications,” BioResources 10(3), 5345-5355. 10.15376/biores.10.3.5345-5355
Derakhshandeh, B., Kerekes, R. J., Hatzikiriakos, S. G., and Bennington, C. P. J. (2011). “Rheology of pulp fibre suspensions: A critical review,” Chem. Eng. Sci. 66, 3460-3470. DOI: 10.1016/j.ces.2011.04.017
Derakhshandeh, B., Petekidis, G., Sabet, S. S., Hamad, W. Y., and Hatzikiriakos, S. G., (2013). “Ageing, yielding, and rheology of nanocrystalline cellulose suspensions,” J. Rheology 57(1), 131-148. DOI: 10.1122/1.4764080
Dhont, J. K. G., and Briels, W. J. (2003). “Viscoelasticity of suspensions of long, rigid rods,” Colloids Surf. A 213(2–3), 131-156. DOI: 10.1016/S0927-7757(02)00508-3
Dimic-Misic, K., Gane, P. A. C., and Paltakari, J. (2013a). “Micro- and nanofibrillated cellulose as a rheology modifier additive in CMC-containing pigment-coating formulations,” Ind. Eng. Chem. Res. 52(45), 16066-16083. DOI: 10.1021/ie4028878
Dimic-Misic, K., Liu, G., Maloney, T., and Gane P. (2017a). “Effect of fibril length and surface charge on ultralow shear-induced structuring in micro and nanofibrillated cellulose aqueous suspensions,” Cellulose [SUBMITTED].
Dimic-Misic, K., Hummel, M., Paltakari, J., Sixta, H., Maloney, T., and Gane, P. (2015a). “From colloidal spheres to nanofibrils: Extensional flow properties of mineral pigment and mixtures with micro and nanofibrils under progressive double layer suppression,” J. Colloid Interface Sci. 446, 31-43. DOI: 10.1016/j.jcis.2015.01.004
Dimic-Misic, K., Maloney, T. C., and Gane, P. A. C. (2015b). “Defining a strain-induced time constant for oriented low shear-induced structuring in high consistency MFC/NFC-filler composite suspensions,” J. Appl. Polym. Sci. 132(47), article no. 42827. DOI: 10.1002/app.42827
Dimic-Misic, K., Maloney, T. C., and Gane, P. A. C. (2017b). “Effect of fibril length, aspect ratio and surface charge on ultralow shear-induced structuring in micro and nanofibrillated cellulose aqueous suspensions,” Cellulose [in press].
Dimic-Misic, K., Nieminen, K., Gane, P., Maloney, T., Sixta, H., and Paltakari, J. (2014). “Deriving a process viscosity for complex particulate nanofibrillar cellulose gel-containing suspensions,” Appl. Rheol. 24(3), article no. 35616. DOI: 10.3933/APPLRHEOL-24-35616
Dimic-Misic, K., Puisto, A., Gane, P., Nieminen, K., Alava, M., Paltakari, J., and Maloney, T. (2013b). “The role of MFC/NFC swelling in the rheological behavior and dewatering of high consistency furnishes,” Cellulose 20(6), 2847-2861. DOI: 10.1007/s10570-013-0076-3
Dimic-Misic, K., Puisto, A., Paltakari, J., Alava, M., and Maloney, T. (2013c). “The influence of shear on the dewatering of high consistency nanofibrillated cellulose furnishes,” Cellulose 20(4), 1853-1864. DOI: 10.1007/s10570-013-9964-9
Dimic-Misic, K., Rantanen, J., Maloney, T. C., and Gane, P. A. C. (2016). “Gel structure phase behavior in micro nanofibrillated cellulose containing in situ precipitated calcium carbonate,” J. Appl. Polymer Sci. 133(22), article no. 43486. DOI: 10.1002/app.43486
Dimic-Misic, K., Salo, T., Paltakari, J., and Gane, P. (2014). “Comparing the rheological properties of novel nanofibrillar cellulose-formulated pigment coating colours with those using traditional thickener,” Nordic Pulp Paper Res. J. 29(2), 253-270. DOI: 10.3183/NPPRJ-2014-29-02-p253-270
Divoux, T., Grenard, V., and Manneville, S. (2013). “Rheological hysteresis in soft glassy materials,” Physical Review Letters 110(1), 018304. DOI: 10.1103/PhysRevLett.110.018304
Dong, X. M., and Gray, D. G. (1997). “Effect of counterions on ordered phase formation in suspensions of charged rodlike cellulose crystallites,” Langmuir 13, 2404-2409. DOI: 10.1021/la960724h
Dong, X. M., Kimura, T., Revol, J. F., and Gray, D. G. (1996). “Effects of ionic strength on the isotropic-chiral nematic phase transition of suspensions of cellulose crystallites,” Langmuir 12(8), 2076-2082. DOI: 10.1021/la950133b
Doraiswamy, D., Mujumdar, A. N., Tsao, I., Beris, A. N., Danforth, S. C., and Metzner, A.B. (1991). “The Cox-Merz rule extended: A rheological model for concentrated suspensions and other materials with a yield stress,” Journal of Rheology 35, 647-685. DOI: 10.1122/1.550184
Dougherty, T. J. (1959). “Some problems in the theory of colloids,” PhD thesis, Case Inst. Technol.
Dufresne, A. (2012). “Rheological behavior of nanocellulose suspensions and self-assembly,” in: Nanocellulose: From Nature to High Performance Tailored Materials, A. Dufresne (ed.), pp. 193-194. DOI: 10.1515/9783110254600.193
Dullaert, K., and Mewis, J. (2006). “A structural kinetics model for thixotropy,” J. Non-Newtonian Fluid Mechan. 139, 21-30. DOI: 10.1016/j.jnnfm.2006.06.002
Ebeling, T., Paillet, M., Borsali, R., Diat, O., Dufresne, A., Cavaille, J. Y., et al. (1999). “Shear-induced orientation phenomena in suspensions of cellulose microcrystals, revealed by small angle X-ray scattering,” Langmuir 15(19), 6123-6126. DOI: 10.1021/la990046+
Echeverria, C., Almeida, P. L., Feio, G., Figueirinhas, J. L., Rey, A. D., and Godinho, M. H. (2015). “Rheo-NMR study of water-based cellulose liquid crystal system at high shear rates,” Polymer 65, 18-25 DOI: 10.1016/j.polymer.2015.03.050
Echeverria, C., Fernandes, S. N., Almeida, P. L., and Godinho, M. H. (2016). “Effect of cellulose nanocrystals in a cellulosic liquid crystal behaviour under low shear (regime I): Structure and molecular dynamics,” Eur. Polymer J. 84, 675-684. DOI: 10.1016/j.eurpolymj.2016.10.009
Eichhorn, S. J. (2011). “Cellulose nanowhiskers: Promising materials for advanced applications,” Soft Matter 7, 303-315. DOI: 10.1039/C0SM00142B
Eichhorn, S. J., Dufresne, A., Aranguren, M., Marcovich, N. E., Capadona, J. R., Rowan, S. J., Weder, C., Thielemans, W., Roman, M., Renneckar, S., Gindl, W., Veigel, S., Keckes, J., Yano, H., Abe, K., Nogi, M., Nakagaito, A. N. , Mangalam, A., Simonsen, J., Benight, A. S., Bismarck, A., Berglund, L. A., and Peijs, T. (2010). “Review: Current international research into cellulose nanofibres and nanocomposites,” J. Mater. Sci. 45(1), 1-33. DOI: 10.1007/s10853-009-3874-0
Einstein, A. (1911). “Berichtigung zu meiner Arbeit: Eine neue Bestimmung der Molekul Dimensionen,” Ann. Phys. 34(3), 591-592. DOI: 10.1002/andp.19113390313
Elazzouzi-Hafraoui, S., Nishiyama, Y., Putaux, J. L., Heux, L., Dubreuil, F., and Rochas, C. (2008). “The shape and size distribution of crystalline nanoparticles prepared by acid hydrolysis of native cellulose,” Biomacromol. 9(1), 57-65. DOI: 10.1021/bm700769p
El Baradai, O., Beneventi, D., Alloin, F., Bongiovanni, R., Bruas-Reverdy, N., Bultel, Y., and Chaussy, D. (2016). “Microfibrillated cellulose based ink for eco-sustainable screen printed flexible electrodes in lithium ion batteries,” J. Mater. Sci. Technol. 32(6), 566-572. DOI: 10.1016/j.jmst.2016.02.010
El Miri, N., Abdelouandi, K., Barakat, A., Zahouily, M., Fihri, A., Solhy, A., and El Achaby, M. (2015). “Bio-nanocomposite films reinforced with cellulose nanocrystals: Rheology of film-forming solutions, transparency, water vapor barrier and tensile properties of films,” Carbohydr. Polym. 129, 156-167. DOI: 10.1016/j.carbpol.2015.04.051
Eyholzer, C., Bordeanu, N., Lopez-Suevos, F., Rentsch, D., Zimmermann, T., and Oksman, K. (2010). “Preparation and characterization of water-redispersible nanofibrillated cellulose in powder form,” Cellulose 17(1), 19-30. DOI: 10.1007/s10570-009-9372-3
Fall, A. B., Lindström, S. B., Sprakel, J., and Wågberg, L. (2013). “A physical cross-linking process of cellulose nanofibril gels with shear controlled fibril orientation,” Soft Matter 9, 1852-1863. DOI: 10.1039/c2sm27223g
Fall, A. B., Lindström S. B., Sundman, O., Ödberg, L., and Wågberg, L. (2011). “Colloidal stability of aqueous nanofibrillated cellulose dispersions,” Langmuir 27, 11332-11338. DOI:10.1021/la201947x
Feng, X. C., Ullah, N., Wang, X. J., Sun, X. C., Li, C. Y., Bai, Y., Chen, L., and Li, Z. X. (2015). “Characterization of bacterial cellulose by Gluconacetobacter hansenii CGMCC 3917,” J. Food Sci. 80(10), E2217-E2227. DOI: 10.1111/1750-3841.13010
Férec, J., and Ausias, G. (2015). “Rheological modeling of non-dilute rod suspensions,” in: Rheology of Non-Spherical Particle Suspensions, Chinesta, F., and Ausias, G. (eds.), Elsevier, Ch. 4, pp. 77-117. DOI: 10.1016/B978-1-78548-036-2.50004-6
Férec, J., Ausias, G., Heuzey, M. C., and Carreau, P. J. (2009). “Modeling fiber interactions in semiconcentrated fiber suspensions,” J. Rheol. 53, 49-72. DOI: 10.1122/1.3000732
Ferrer, A., Salas, C., and Rojas, O. J. (2016). “Physical, thermal, chemical and rheological characterization of cellulosic microfibrils and microparticles produced from soybean hulls,” Indust. Crops Prod. 84, 337-343. DOI: 10.1016/j.indcrop.2016.02.014
Fink, H. P., Weigel, P., Purz, H. J., and Ganster, J. (2001). “Structure formation of regenerated cellulose materials from NMMO-solutions,” Prog. Polym. Sci. 26(9), 1473-1524. DOI: 10.1016/S0079-6700(01)00025-9
Frensemeier, M., Koplm, C., Jaeger, R., Kramer, F., and Klemm, D. (2010). “Mechanical properties of bacterially synthesized nanocellulose hydrogels,” in: Utilization of Lignocellulosic Materials, T. Heinze, M. Janura, and A. Koschella (eds.), Macromol. Symp. 294-II, 38-44. DOI: 10.1002/masy.200900030
Fukuzumi, H., Tanaka, R., Saito, T., and Isogai, A. (2014). “Dispersion stability and aggregation behavior of TEMPO-oxidized cellulose nanofibrils in water as a function of salt addition,” Cellulose 21(3), 1553-1559. DOI: 10.1007/s10570-014-0180-z
Gallier, S., Lemaire, E., Peters, F., and Lobry, L. (2014). “Rheology of sheared suspensions of rough frictional particles,” J. Fluid Mech. 757, 514-549. DOI: 10.1017/jfm.2014.507
Gao, X., Kusmierczyk, P., Shi, Z. J., Liu, C. Q., Yang, G., Sevostianov, I., and Silberschmidt, V. V. (2016a). “Through-thickness stress relaxation in bacterial cellulose hydrogel,” J. Mechan. Behav. Biomed. Mater. 59, 90-98. DOI: 10.1016/j.jmbbm.2015.12.021
Gao, X., Shi, Z. J., Kusmierczyk, P., Liu, C. Q., Yang, G., Sevostianov, I., and Silberschmidt, V. V. (2016b). “Time-dependent rheological behaviour of bacterial cellulose hydrogel,” Mater. Sci. Eng. C – Mater. Biol. Appl. 58, 153-159. DOI: 10.1016/j.msec.2015.08.019
Going, R. J., Ayranci, C., and Sameoto, D. E. (2015). “Dispersion of cellulose nanocrystals in a water-methanol co-solvent system,” in: Design, Manufacturing and Applications of Composites, R. Vaziri, A. Nakai, B. Crawford, M. Hojjati, T. Kosaka, and S. Hoa (eds.), Univ British Columbia, pp. 240-247.
Gomez, C., Serpa, A., Velasquez-Cock, J., Ganan, P., Castro, C., Velez, L., and Zuluaga, R. (2016). “Vegetable nanocellulose in food science: A review,” Food Hydrocolloids 57, 178-186. DOI: 10.1016/j.foodhyd.2016.01.023
Gong, G. A., Mathew, A. P., and Oksman, K. (2011). “Strong aqueous gels of cellulose nanofibers and nanowhiskers isolated from softwood flour,” TAPPI J. 10(2), 7-14.
González-Labrada, E., and Gray, D. G. (2012). “Viscosity measurements of dilute aqueous suspensions of cellulose nanocrystals using a rolling ball viscometer,” Cellulose 19(5), 1557-1565. DOI: 10.1007/s10570-012-9746-9
Gousse, C., Chanzy, H., Cerrada, M. L., and Fleury, E. (2004). “Surface silylation of cellulose microfibrils: Preparation and rheological properties,” Polymer 45(5), 1569-1575. DOI: 10.1016/j.polymer.2003.12.028
Gray, D. G., and Mu, X. Y. (2016). “Twist-bend stage in the relaxation of sheared chiral nematic suspensions of cellulose nanocrystals,” ACS Omega 1(2), 212-219. DOI: 10.1021/acsomega.6b00100
Gruneberger, F., Kunniger, T., Zimmermann, T., and Arnold, M. (2014). “Rheology of nanofibrillated cellulose/acrylate systems for coating applications,” Cellulose 21(3), 1313-1326. DOI: 10.1007/s10570-014-0248-9
Gu, J., Catchmark, J. M., Kaiser, E. Q., and Archibald, D. D. (2013). “Quantification of cellulose nanowhiskers sulfate esterification levels,” Carbohydrate Polymers 92(2), 1809-1816. DOI: 10.1016/j.carbpol.2012.10.078
Gudarzi, M., Trefalt, G., Szilagyi, I., and Maroni, P. (2015). “Forces between negatively charged interfaces in the presence of cationic multivalent oligoamines measured with the atomic force microscope,” J. Phys. Chem. 119(27), 15482-15490. DOI: 10.1021/acs.jpcc.5b04426
Guinnaraes, M., Botaro, V. R., Novack, K. M., Neto, W. P. F., Mendes, L. M., and Tonoli, G. H. D. (2015). “Preparation of cellulose nanofibrils from bamboo pulp by mechanical defibrillation for their applications in biodegradable composites,” J. Nanosci. Nanotech. 15(9), 6751-6768. DOI: 10.1166/jnn.2015.10854
Guo, R., and Ding, E. Y. (2006). “Rheological and DSC studies on the interaction between kappa-carrageenan and cellulose nanocrystals (CNC),” Chinese Chem. Lett. 17(5), 695-698.
Haavisto, S., Salmela, J., Jasberg, A., Saarinen, T., Karppinen, A., and Koponen, A. (2015). “Rheological characterization of microfibrillated cellulose suspension using optical coherence tomography,” TAPPI J. 14(5), 291-302.
Hakansson, K. M. O., Lundell, F., Prahl-Wittberg, L., and Soderberg, L. D. (2016). “Nanofibril alignment in flow focusing: Measurements and calculations,” J. Phys. Chem. B 120(27), 6674-6686. DOI: 10.1021/acs.jpcb.6b02972
Hambardzumyan, A., Foulon, L., Bercu, N. B., Pernes, M., Maigret, J. E., Molinari, M., Chabbert, B., and Aguie-Beghin, V. (2015). “Organosolv lignin as natural grafting additive to improve the water resistance of films using cellulose nanocrystals,” Chem. Eng. J. 264, 780-788. DOI: 10.1016/j.cej.2014.12.004
Hasani, M., Cranston, E. D., and Westman, G., and Gray, D. G. (2008). “Cationic surface functionalization of cellulose nanocrystals,” Soft Matter 4(11), 2238-2244. DOI: 10.1039/b806789a
Hassan, M. L., Hassan, E. A., and Oksman, K. N. (2011). “Effect of pretreatment of bagasse fibers on the properties of chitosan/microfibrillated cellulose nanocomposites,” Journal of Materials Science 46(6), 1732-1740. DOI: 10.1007/s10853-010-4992-4
Heggset, E. B., Chinga-Carrasco, G., and Syverud, K. (2017). “Temperature stability of nanocellulose dispersions,” Carbohyd. Polym. 157, 114-121. DOI: 10.1016/j.carbpol.2016.09.077
Hellström, P., Heijnesson-Hultén, A., Paulsson, M., Håkansson, H., and Germgård, U. (2014). “The effect of Fenton chemistry on the properties of microfibrillated cellulose,” Cellulose 21(3), 1489-1503. DOI: 10.1007/s10570-014-0243-1
Hellström, P., Heijnesson-Hulten, A., Paulsson, M., Hakansson, H., and Germgard, U. (2016). “A comparative study of enzymatic and Fenton pretreatment applied to a birch kraft pulp used for MFC production in a pilot scale high-pressure homogenizer,” TAPPI J. 15(6), 375-381.
Hiasa, S., Kumagai, A., Endo, T., and Edashige, Y. (2016). “Prevention of aggregation of pectin-containing cellulose nanofibers prepared from mandarin peel,” J. Fiber Sci. Technol. 72(1), 17-26. DOI: 10.2115/fiberst.2016-0006
Hiemenz, P., and Rajagopalan, R. (1997). Principles of Colloid and Surface Chemistry, 3rd Ed, Marcel Dekker, New York. DOI: 10.1201/9781315274287
Hill, R. J. (2008). “Elastic modulus of microfibrillar cellulose gels,” Biomacromolecules 9(10), 2963-2966. DOI: 10.1021/bm800490x
Hirota, M., Tamura, N., Saito, T., and Isogai, A. (2010). “Water dispersion of cellulose II nanocrystals prepared by TEMPO-mediated oxidation of mercerized cellulose at pH 4.8,” Cellulose 17(2), 279-288. DOI: 10.1007/s10570-009-9381-2
Hoeng, F., Denneulin, A., and Bras, J. (2016). “Use of nanocellulose in printed electronics: A review,” Nanoscale 8(27), 13131-13154. DOI: 10.1039/c6nr03054h
Hoeng, F., Denneulin, A., Reverdy-Bruas, N., Krosnicki, G., and Bras, J. (2017). “Rheology of cellulose nanofibrils/silver nanowires suspension for the production of transparent and conductive electrodes by screen printing,” Appl. Surf. Sci. 394, 160-168. DOI: 10.1016/j.apsusc.2016.10.073
Honorato, C., Kumar, V., Liu, J., Koivula, H., Xu, C. L., and Toivakka, M. (2015). “Transparent nanocellulose-pigment composite films,” J. Mater. Sci. 50(22), 7343-7352. DOI: 10.1007/s10853-015-9291-7
Horvath, A. E., and Lindström, T. (2007). “The influence of colloidal interactions on fiber network strength,” J. Colloid Interface Sci. 309, 511-517. DOI: 10.1016/j.jcis.2006.08.066
Hu, Z., Cranston, E. D., Ng, R., and Pelton, R. (2014). “Tuning cellulose nanocrystal gelation with polysaccharides and surfactants,” Langmuir 30(10), 2684-2692. DOI: 10.1021/la404977t
Hubbe, M. A. (1984). “Theory of detachment of colloidal particles from flat surfaces exposed to flow,” Colloids and Surfaces 12(1-2), 151-178. DOI: 10.1016/0166-6622(84)80096-7
Hubbe, M. A. (2005). “Microparticle programs for drainage and retention,” in: Micro and Nanoparticles in Papermaking, Rodriguez, J. M. (ed.), TAPPI Press, Atlanta, Chapter 1, 1-36.
Hubbe, M. A. (2007). “Flocculation and redispersion of cellulosic fiber suspensions: A review of effect of hydrodynamic shear and polyelectrolytes,” BioResources 2, 296-331. DOI: 10.15376/biores.2.2.296-331
Hubbe, M. A., Ferrer, A., Tyagi, P., Yin, Y., Salas, C., Pal, L., and Rojas, O. J. (2017). “Nanocellulose in thin films, coatings, and plies for packaging applications: A review,” BioResources 12(1), 2143-2233. DOI: 10.15376/biores.12.1.2143-2233
Hubbe, M. A., and Rojas, O. J. (2008). “Colloidal stability and aggregation of lignocellulosic materials in aqueous suspension: A review,” BioResources 3(4), 1419-1491. DOI: 10.15376/biores.3.4.1419-1491
Hubbe, M. A., Rojas, O. J., Lucia, L. A., and Sain, M. (2008). “Cellulosic nanocomposites, A review,” BioResources 3(3), 929-980. DOI: 10.15376/biores.3.3.929-980
Hubbe, M. A., Venditti, R. A., and Rojas, O. J. (2007). “What happens to cellulosic fibers during papermaking and recycling? A review,” BioResources 2(4), 739-788. DOI: 10.15376/biores.2.4.739-788
Iguchi, M., Yamanaka, S., and Budhiono, A. (2000). “Bacterial cellulose—A masterpiece of nature’s arts,” Journal of Materials Science 35(2), 261-270. DOI: 10.1023/A:1004775229149
Illa, X., Puisto, A., Lehtinen, A., Mohtaschemi, M., and Alava, M. J. (2013). “Transient shear banding in time-dependent fluids,” Phys. Rev. E 87(2), article no. 022307. DOI: 10.1103/PhysRevE.87.022307
Ioelovich, M. (2014). “Peculiarities of cellulose nanoparticles,” TAPPI J. 13(5), 45-51.
Iotti, M., Gregersen, O. W., Moe, S., and Lenes, M. (2011). “Rheological studies of microfibrillar cellulose water dispersions,” J. Polymers Environ. 19(1), 137-145. DOI: 10.1007/s10924-010-0248-2
Ishii, D., Saito, T., and Isogai, A. (2011). “Viscoelastic evaluation of average length of cellulose nanofibers prepared by TEMPO-mediated oxidation,” Biomacromolecules 12(3), 548-550. DOI: 10.1021/bm1013876
Isogai, A. (2015). “Structural characterization and modifications of surface-oxidized cellulose nanofiber,” J. Japan Petrol. Inst. 58(6), 365-375. DOI: 10.1627/jpi.58.365
Isogai, A., Saito, T., and Fukuzumi, H. (2011). “TEMPO-oxidized cellulose nanofibers,” Nanoscale 3(1), 71-85. DOI: 10.1039/C0NR00583E
Israelachvili, J. N. (2011). Intermolecular and Surface Forces, 3rd Ed., Academic Press, Burlington, MA.
Israelachvili, J., and Wennerstrom, H. (1996). “Role of hydration and water structure in biological and colloidal interactions,” Nature 379)6562), 219-225. DOI: 10.1038/379219a0
Iwamoto, S., Lee, S. H., and Endo, T. (2014). “Relationship between aspect ratio and suspension viscosity of wood cellulose nanofibers,” Polym. J. 46(1), 73-76. DOI: 10.1038/pj.2013.64
Jia, X. J., Chen, Y. W., Shi, C., Ye, Y. F., Abid, M., Jabbar, S., Wang, P., Zeng, X. X., and Wu, T. (2014). “Rheological properties of an amorphous cellulose suspension,” Food Hydrocolloids 39, 27-33. DOI: 10.1016/j.foodhyd.2013.12.026
Jiang, F., and Hsieh, Y.-L. (2014). “Assembling and redispersibility of rice straw nanocellulose: Effect of tert-butanol,” ACS Appl. Mater. Interfaces 6, 20075-20084. DOI: 10.1021/am505626a
Jin, Y., Hengl, N., Baup, S., Pignon, F., Gondrexon, N., Sztucki, M., Romdhane, A., Guillet, A., and Aurousseau, M. (2015). “Ultrasonic assisted cross-flow ultrafiltration of starch and cellulose nanocrystals suspensions: Characterization at multi-scales,” Carbohydr. Polym. 124, 66-76. DOI: 10.1016/j.carbpol.2015.01.073
Johnson, R. K., Zink-Sharp, A., Renneckar, S. H., and Glasser, W. G. (2009). “A new bio-based nanocomposite: Fibrillated TEMPO-oxidized celluloses in hydroxypropylcellulose matrix,” Cellulose 16(2), 227-238. DOI: 10.1007/s10570-008-9269-6
Jonas, R., and Farah, L. F. (1998). “Production and application of microbial cellulose,” Polym. Degrad. Stability 59, 101-106. DOI: 10.1016/S0141-3910(97)00197-3
Joutsimo, O. P., and Giacomozzi, D. (2015). “Changes in cell wall structure during kraft processing of Pinus radiata,” BioResources 10(2), 2461-2478. DOI: 10.15376/biores.10.2.2461-2478
Jowkarderis, L., and van de Ven, T. G. M. (2014). “Intrinsic viscosity of aqueous suspensions of cellulose nanofibrils,” Cellulose 21(4), 2511-2517. DOI: 10.1007/s10570-014-0292-5
Jowkarderis, L., van de Ven, T. G. M. (2015). “Rheology of semi-dilute suspensions of carboxylated cellulose nanofibrils,” Carbohydr. Polymers 123, 416-423. DOI: 10.1016/j.carbpol.2015.01.067
Kamel, S. (2007). “Nanotechnology and its applications in lignocellulosic composites, a mini review,” Express Polymer Lett. 1(9), 546-575. DOI: 10.3144/expresspolymlett.2007.78
Kangas, H., Lahtinen, P., Sneck, A., Saariaho, A. M., Laitinen, O., and Hellen, E. (2014). “Characterization of fibrillated celluloses. A short review and evaluation of characteristics with a combination of methods,” Nordic Pulp Paper Res. J. 29(1), 129-143. DOI: 10.3183/NPPRJ-2014-29-01-p129-143
Karppinen, A., Saarinen, T., Salmela, J., Laukkanen, A., Nuopponen, M., and Seppala, J. (2012). “Flocculation of microfibrillated cellulose in shear flow,” Cellulose 19(6), 1807-1819. DOI: 10.1007/s10570-012-9766-5
Karppinen, A., Vesterinen, A. H., Saarinen, T., Pietikainen, P., and Seppala, J. (2011). “Effect of cationic polymethacrylates on the rheology and flocculation of microfibrillated cellulose,” Cellulose 18(6), 1381-1390. DOI: 10.1007/s10570-011-9597-9
Kekalainen, K., Liimatainen, H., Biale, F., and Niinimaki, J. (2015). “Nanofibrillation of TEMPO-oxidized bleached hardwood kraft cellulose at high solids content,” Holzforschung 69(9), 1077-1088. DOI: 10.1515/hf-2014-0269
Kekalainen, K., Liimatainen, H., Illikainen, M., Maloney, T. C., and Niinimaki, J. (2014a). “The role of hornification in the disintegration behaviour of TEMPO-oxidized bleached hardwood fibres in a high-shear homogenizer,” Cellulose 21(3), 1163-1174. DOI: 10.1007/s10570-014-0210-x
Kekalainen, K., Liimatainen, H., and Niinimaki, J. (2014b). “Disintegration of periodate-chlorite oxidized hardwood pulp fibres to cellulose microfibrils: Kinetics and charge threshold,” Cellulose 21(5), 3691-3700. DOI: 10.1007/s10570-014-0363-7
Kerekes, R. J. (2006). “Rheology of fibre suspensions in papermaking: An overview of recent research,” Nord. Pulp Pap. Res. J. 21(5), 598-612. DOI: 10.3183/NPPRJ-2006-21-05-p598-612
Kerekes, R. J., and Schell, C. J. (1992). “Characterization of fiber flocculation regimes by a crowding factor,” J. Pulp Paper Sci. 18(1), J32-J38.
Keshtkar, M., Heuzey, M. C., and Carreau, P. J. (2009). “Rheological behavior of fiber-filled model suspensions: Effect of fiber flexibility,” J. Rheol. 53(3), 631-650. DOI: 10.1122/1.3103546
Khan, R. A., Salmieri, S., Dussault, D., Uribe-Calderon, J., Kamal, M. R., Safrany, A., and Lacroix, M. (2010). “Production and properties of nanocellulose-reinforced methylcellulose-based biodegradable films,” J. Agric. Food Chem. 58(13), 7878-7885. DOI: 10.1021/jf1006853
Khoshkava, V., and Kamal, M. R. (2014). “Effect of drying conditions on cellulose nanocrystal (CNC) agglomerate porosity and dispersibility in polymer nanocomposites,” Powder Technol. 261, 288-298. DOI: 10.1016/j.powtec2014.04.016
Kim, D. H., and Song, Y. S. (2015). “Rheological behavior of cellulose nanowhisker suspension under magnetic field,” Carbohydrate Polymers 126, 240-247. DOI: 10.1016/j.carbpol.2015.03.026
Kim, S., and Lee, J. (2010). “Effective polymeric dispersants for vacuum, convection and freeze drying of drug nanosuspensions,” Int. J. Pharm. 397, 218-224. DOI: 10.1016/j.ijpharm.2010.07.010
Klemm, D., Kramer, F., Moritz, S., Lindstrom, T., Ankerfors, M., Gray, D., and Dorris, A. (2011). “Nanocelluloses: A new family of nature-based materials,” Angewandte Chemie – Int. Ed. 50(24), 5438-5466. DOI: 10.1002/anie.201001273
Kontturi, E., and Vuorinen, T. (2008). “Indirect evidence of supramolecular changes within cellulose microfibrils of chemical pulp fibers upon drying,” Cellulose 16(1), 64-74. DOI 10.1007/s10570-008-9235-3
Korhonen, M. H. J., Sorvari, A., Saarinen, T., Seppala, J., and Laine, J. (2014). “Deflocculation of cellulosic suspensions with anionic high molecular weight polyelectrolytes,” BioResources 9(2), 3550-3570. DOI: 10.15376/biores.9.2.3550-3570
Korson, L., Drosthan, W., and Millero, F. J. (1969). “Viscosity of water at various temperatures,” J. Phys. Chem. 73(1), 34-39. DOI: 10.1021/j100721a006
Kratohvil, S., Janauer, G. E., and Matijević, E. (1969). “Coagulation of microcrystalline cellulose dispersions,” J. Colloid Interface Sci. 29(2), 187-193. DOI:10.1016/0021-9797(69)90185-4
Krieger, I. M. (1959). “A mechanism for non-Newtonian flow in suspensions of rigid spheres,” Trans. Soc. Rheol. 3, 137-152. DOI: 10.1122/1.548848
Krieger, I. M. (1972). “Rheology of monodisperse latices,” Adv. Colloid Interface Sci. 3(2), 111-136. DOI: 10.1016/0001-8686(72)80001-0
Kumar, V., Elfving, A., Koivula, H., Bousfield, D., and Toivakka, M. (2016a). “Roll-to-roll processed cellulose nanofiber coatings,” Indust. Eng. Chem. Res. 55(12), 3603-3613. DOI: 10.1021/acs.iecr.6b00417
Kumar, V., Nazari, B., Bousfield, D., and Toivakka, M. (2016b). “Rheology of microfibrillated cellulose suspensions in pressure-driven flow,” Applied Rheol. 26(4), article no. 43534. DOI: 10.3933/ApplRheol-26-43534
Kumar, V., Koppolu, V. R., Bousfield, D., and Toivakka, M. (2017). “Substrate role in coating of microfibrillated cellulose suspensions,” Cellulose 24(3), 1247-1260. DOI: 10.1007/s10570-017-1201-5
Landauer, R. (1978). “Electrical transport and optical properties of inhomogeneous media,” in: J. C. Garland and D. B. Tanner (eds,), AIP Conf. Proc. No 40, American Institute of Physics, New-York, pp 2-43.
Larson, R. G. (2005). “The rheology of dilute solutions of flexible polymers: Progress and problems,” J. Rheol. 49(1), 1-70. DOI: 10.1122/1.1835336
Lasseuguette, E. (2008). “Grafting onto microfibrils of native cellulose,” Cellulose 15(4), 571-580. DOI: 10.1007/s10570-008-9200-1
Lasseuguette, E., Roux, D., and Nishiyama, Y. (2008). “Rheological properties of microfibrillar suspension of TEMPO-oxidized pulp,” Cellulose 15(3), 425-433. DOI: 10.1007/s10570-007-9184-2
Lavoine, N., Desloges, I., Dufresne, A., and Bras, J. (2012). “Microfibrillated cellulose: Its barrier properties and applications in cellulosic materials: A review,” Carbohyd. Polym. 90, 735-764. DOI: 10.1016/j.carbpol.2012.05.026
Lee, K. Y., and Bismarck, A. (2012). “Susceptibility of never-dried and freeze-dried bacterial cellulose towards esterification with organic acid,” Cellulose 19(3), 891-900. DOI: 10.1007/s10570-012-9680-x
Le Goff, K. J., Jouanneau, D., Garnier, C., and Aubry, T. (2014). “Gelling of cellulose nanowhiskers in aqueous suspension,” J. Appl. Polymer Sci. 131(17), article no. 40676. DOI: 10.1002/app.40676
Lenfant, G., Heuzey, M. C., van de Ven, T. G. M., and Carreau, P. (2015). “Intrinsic viscosity of suspensions of electrosterically stabilized nanocrystals of cellulose,” Cellulose 22(2), 1109-1122. DOI: 10.1007/s10570-015-0573-7
Lenze, C. J., Peksa, C. A., Sun, W. M., Hoeger, I. C., Salas, C., and Hubbe, M. A. (2016). “Intact and broken cellulose nanocrystals as model nanoparticles to promote dewatering and fine-particle retention during papermaking,” Cellulose 23(6), 3951-3962. DOI: 10.1007/s10570-016-1077-9
Leung, A. C. W., Hrapovic, S., Lam, E., Liu, Y. L., Male, K. B., Mahmoud, K. A., and Luong, J. H. T. (2011). “Characteristics and properties of carboxylated cellulose nanocrystals prepared from a novel one-step procedure,” Small 7(3), 302-305. DOI: 10.1002/smll.201001715
Lewis, L., Derakhshandeh, M., Hatzikiriakos, S. G., Hamad, W. Y., and MacLachlan, M. J. (2016). “Hydrothermal gelation of aqueous cellulose nanocrystal suspensions,” Biomacromol. 17(8), 2747-2754. DOI: 10.1021/acs.biomac.6b00906
Li, B., Xu, W. Y., Kronlund, D., Maattanen, A., Liu, J., Smatt, J. H., Peltonen, J., Willfor, S., Mu, X. D., and Xu, C. L. (2015a). “Cellulose nanocrystals prepared via formic acid hydrolysis followed by TEMPO-mediated oxidation,” Carbohyd. Polym. 133, 605-612. DOI: 10.1016/j.carbpol.2015.07.033
Li, J. H., Wei, X. Y., Wang, Q. H., Chen, J. C., Chang, G., Kong, L. X., Su, J. B., and Liu, Y. H. (2012). “Homogeneous isolation of nanocellulose from sugarcane bagasse by high pressure homogenization,” Carbohydr. Polym. 90(4), 1609-1613. DOI: 10.1016/j.carbpol.2012.07.038
Li, M. C., Wu, Q. L., Song, K. L., Lee, S., Qing, Y., and Wu, Y. Q. (2015b). “Cellulose nanoparticles: Structure-morphology-rheology relationships,” ACS Sustain. Chem. Eng. 3(5), 821-832. DOI: 10.1021/acssuschemeng.5b00144
Li, M. C., Wu, Q. L., Song, K. L., De Hoop, C. F., Lee, S., Qing, Y., and Wu, Y. Q. (2016). “Cellulose nanocrystals and polyanionic cellulose as additives in bentonite water-based drilling fluids: Rheological modeling and filtration mechanisms,” Indust. Eng. Chem. Res. 55(1), 133-143. DOI: 10.1021/acs.iecr.5b03510
Li, M. C., Wu, Q. L., Song, K. L., Qing, Y., and Wu, Y. Q. (2015c). “Cellulose nanoparticles as modifiers for rheology and fluid loss in bentonite water-based fluids,” ACS Appl. Mater. Interfaces 7(8), 5006-5016. DOI: 10.1021/acsami.5b00498
Liang, Y., Hilal, N., Langston, P., and Starov, V. (2007). “Interaction forces between colloidal particles in liquid: Theory and experiment,” Advan. Colloid Interface Sci. 134-135, 151-166. DOI: 10.1016/j.cis.2007.04.003
Lima, M. M. D., and Borsali, R. (2004). “Rodlike cellulose microcrystals: Structure, properties, and applications,” Macromol. Rapid Commun. 25(7), 771-787. DOI: 10.1002/marc.200300268
Lin, D. H., Li, R., Lopez-Sanchez, P., and Li, Z. X. (2015). “Physical properties of bacterial cellulose aqueous suspensions treated by high pressure homogenizer,” Food Hydrocolloids 44, 435-442. DOI: 10.1016/j.foodhyd.2014.10.019
Lindström, T. (2017). “Aspects on nanofibrillated cellulose (NFC) processing, rheology and NFC-film properties,” Current Opin. Colloid Interface Sci. 29, 68-75. DOI: 10.1016/j.cocis.2017.02.005
Lindström, T., and Aulin, C. (2014). “Market and technical challenges and opportunities in the area of innovative new materials and composites based on nanocellulosics,” Scan. J. Forest Res. 29(4), 345-351. DOI: 10.1080/02827581.2014.928365
Liu, D. G., Chen, X. Y., Yue, Y. Y., Chen, M. D., and Wu, Q. L. (2011). “Structure and rheology of nanocrystalline cellulose,” Carbohyd. Polym. 84(1), 316-322. DOI: 10.1016/j.carbpol.2010.11.039
Liu, D. G., Wang, S., Ma, Z. S., Tian, D. L, Gu, M. Y., and Lin, F. Y. (2014). “Structure-color mechanism of iridescent cellulose nanocrystal films,” RSC Adv. 4, article 39322. DOI: 10.1039/c4ra06268j
Loranger, E., Jradi, K., and Daneault, C. (2012a). “Nanocellulose production by ultrasound-assisted TEMPO oxidation of kraft pulp on laboratory and pilot scales,” IEEE International Ultrasonics Symposium, pp. 953-956. DOI: 10.1109/ULTSYM.2012.0238
Loranger, E., Piche, A. O., and Daneault, C. (2012b). “Influence of high shear dispersion on the production of cellulose nanofibers by ultrasound-assisted tempo-oxidation of kraft pulp,” Nanomater. 2(3), 286-297. DOI: 10.3390/nano2030286
Lowys, M. P., Desbrieres, J., and Rinaudo, M. (2001). “Rheological characterization of cellulosic microfibril suspensions. Role of polymeric additives,” Food Hydrocolloids 15(1), 25-32. DOI: 10.1016/S0268-005X(00)00046-1
Lu, A., Hemraz, U., Khalili, Z., and Boluk, Y. (2014a). “Unique viscoelastic behaviors of colloidal nanocrystalline cellulose aqueous suspensions,” Cellulose 21(3), 1239-1250. DOI: 10.1007/s10570-014-0173-y
Lu, A., Song, Y. B., and Boluk, Y. (2014b). “Electrolyte effect on gelation behavior of oppositely charged nanocrystalline cellulose and polyelectrolyte,” Carbohydr. Polym. 114, 57-64. DOI: 10.1016/j.carbpol.2014.07.040
Lu, A., Wang, Y. X., and Boluk, Y. (2014c). “Investigation of the scaling law on gelation of oppositely charged nanocrystalline cellulose and polyelectrolyte,” Carbohydr. Polymers 105, 214-221. DOI: 10.1016/j.carbpol.2014.01.077
Lucander, M., Asikainen, S., Pohler, T., Saharinen, E., and Bjorkqvist, T. (2009). “Fatigue treatment of wood by high-frequency cyclic loading,” J. Pulp Paper Sci. 35(3-4), 81-85.
Mahbubul, I. M., Saidur, R., and Amalina, M. A. (2012), “Latest developments on the viscosity of nanofluids,” Intl. J. Heat Mass Transfer 55(4), 874-885. DOI: 10.1016/j.ijheatmasstransfer.2011.10.021
Majoinen, J., Hassinen, J., Haataja, J. S.., Rekola, H. T., Kontturi, E., Kostiainen, M. A., Ras, R. H. A., Törmä, P., and Ikkala, O. (2016). “Chiral plasmonics using twisting along cellulose nanocrystals as a template for gold nanoparticles,” Advan. Mater. 28(26), 5262-5267. DOI: 10.1002/adma.201600940
Malkin, A. Y. (2017). Rheology: Concepts, Methods, and Applications, Elsevier. ISBN: 978-1-927885-21-5
Marchessault, R. H., Morehead, F. F., and Koch, M. J. (1961). “Some hydrodynamic properties of neutral suspensions of cellulose crystallites as related to size and shape,” J. Colloid Sci. 16(4), 327-344. DOI: 10.1016/0095-8522(61)90033-2
Mariano, M., El Kissi, N., and Dufresne, A. (2014). “Cellulose nanocrystals and related nanocomposites: Review of some properties and challenges,” J. Polym. Sci. Part B – Polym. Phys. 52(12), 791-806. DOI: 10.1002/polb.23490
Marcus, P. S. (1984). “Simulation of Taylor-Couette flow. 1. Numerical methods and comparison with experiment,” J. Fluid Mechan. 146, 45-64. DOI: 10.1017/S0022112084001762
Maron, S. H., and Pierce, P. E. (1956). “Application of Ree-Eyring generalized flow theory to suspensions of spherical particles,” J. Colloid Sci. 11, 80-95. DOI: 10.1016/0095-8522(56)90023-X
Martoia, F., Dumont, P. J. J., Orgeas, L., Belgacem, M. N., and Putaux, J. L. (2016). “Micro-mechanics of electrostatically stabilized suspensions of cellulose nanofibrils under steady state shear flow,” Soft Matter 12(6), 1721-1735. DOI: 10.1039/c5sm02310f
Martoia, F., Perge, C., Dumont, P. J. J., Orgeas, L., Fardin, M. A., Manneville, S., and Belgacem, M. N. (2015). “Heterogeneous flow kinematics of cellulose nanofibril suspensions under shear,” Soft Matter 11(24), 4742-4755. DOI: 10.1039/c5sm00530b
Mascheroni, E., Rampazzo, R., Ortenzi, M. A., Piva, G., Bonetti, S., and Piergiovanni, L. (2016). “Comparison of cellulose nanocrystals obtained by sulfuric acid hydrolysis and ammonium persulfate, to be used as coating on flexible food-packaging materials,” Cellulose 23(1), 779-793. DOI: 10.1007/s10570-015-0853-2
Mason, S. G. (1950). “The flocculation of pulp suspensions and the formation of paper,” Tappi 33(9), 440-444.
Mason, S. G. (1954). “Fiber motions and flocculation,” Tappi 37(11), 494-501.
Mathew, A. P., Oksman, K., and Sain, M. (2005). “Mechanical properties of biodegradable composites from poly lactic acid (PLA) and microcrystalline cellulose (MCC),” J. Appl. Polym. Sci. 97(5), 2014-2025. DOI: 10.1002/app.21779
Matsumiya, Y., Watanabe, H., Abe, K., Matsumura, Y., Tani, F., Kase, Y., Kikkawa, S., Suzuki, Y., and Ishii, N. (2017). “Rheology of nano-cellulose fiber suspension,” Nihon Reoroji Gakkaishi 45(1), 3-11. DOI: 10.1678/rheology.45.3
May, P. A., and Moore, J. S. (2013). “Polymer mechanochemistry: Techniques to generate molecular force via elongational flows,” Chem. Soc. Reviews 42(18), 7497-7506. DOI: 10.1039/c2cs35463b
McKinley, G. H., and Sridhar, T. (2002). “Filament-stretching rheometry of complex fluids,” Ann. Rev. Fluid Mechan. 34, 375-415. DOI: 10.1146/annurev.fluid.34.083001.125207
Meree, C. E., Schueneman, G. T., Meredith, J. C., and Shofner, M. L. (2016). “Rheological behavior of highly loaded cellulose nanocrystal/poly(vinyl alcohol) composite suspensions,” Cellulose 23(5), 3001-3012. DOI: 10.1007/s10570-016-1003-1
Mewis, J., and Wagner, N. J. (2009). “Thixotropy,” Adv. Colloid Interface Sci. 147-148, 214. DOI: 10.1016/j.cis.2008.09.005
Mewis, J., and Wagner, N. J. (2012). Colloidal Suspension Rheology, Cambridge University Press, New York.
Meyer, R., and Wahren, D. (1964). “On the elastic properties of three-dimensional fiber networks,” Svensk Papperstidning 67, 432-436.
Mihranyan, A., Edsman, K., and Stromme, M. (2007). “Rheological properties of cellulose hydrogels prepared from Cladophora cellulose powder,” Food Hydrocolloids 21(2), 267-272. DOI: 10.1016/j.foodhyd.2006.04.003
Mishra, S. P., Manent, A. S., Chabot, B., and Daneault, C. (2012). “Production of nanocellulose from native cellulose – Various options utilizing ultrasound,” BioResources 7(1), 422-436. DOI: 10.15376/biores.7.1.0422-0436
Missoum, K., Bras, J., and Belgacem, M. N. (2012a). “Organization of aliphatic chains grafted on nanofibrillated cellulose and influence on final properties,” Cellulose 19(6), 1957-1973. DOI: 10.1007/s10570-012-9780-7
Missoum, K., Bras, J., and Belgacem, M. N. (2012b). “Water redispersible dried nanofibrillated cellulose by adding sodium chloride,” Biomacromol. 13(12), 4118-4125. DOI: 10.1021/bm301378n
Moberg, T., Rigdahl, M., Stading, M., and Bragd, E. L. (2014). “Extensional viscosity of microfibrillated cellulose suspensions,” Carbohyd. Polym. 102, 409-412. DOI: 10.1016/j.carbpol.2013.11.041
Moberg, T., Sahlin, K., Yao, K., Geng, S. Y., Westman, G., Zhou, Q., Oksman, K., and Rigdahl, M. (2017). “Rheological properties of nanocellulose suspensions: Effects of fibril/particle dimensions and surface characteristics,” Cellulose 24(6), 2499-2510. DOI: 10.1007/s10570-017-1283-0
Mohtaschemi, M., Dimic-Misic, K., Puisto, A., Korhonen, M., Maloney, T., Paltakari, J., and Alava, M. J. (2014a). “Rheological characterization of fibrillated cellulose suspensions via bucket vane viscometer,” Cellulose 21(3), 1305-1312. DOI: 10.1007/s10570-014-0235-1
Mohtaschemi, M., Sorvari, A., Puisto, A., Nuopponen, M., Seppala, J., and Alava, M. J. (2014b). “The vane method and kinetic modeling: Shear rheology of nanofibrillated cellulose suspensions,” Cellulose 21(6), 3913-3925. DOI: 10.1007/s10570-014-0409-x
Mongruel, A., and Cloitre, M. (1999). “Shear viscosity of suspensions of aligned non-Brownian fibres,” Rheol. Acta 38, 451-457. DOI: 10.1007/s003970050196
Moon, R. J., Martini, A., Nairn, J., Simonsen, J., and Youngblood, J. (2011). “Cellulose nanomaterials review: Structure, properties and nanocomposites,” Chem. Soc. Rev. 40, 3941-3994. DOI: 10.1039/c0cs00108b
Moser, C., Lindstrom, M. E., and Henriksson, G. (2015). “Toward industrially feasible methods for following the process of manufacturing cellulose nanofibers,” BioResources 10(2), 2360-2375. DOI: 10.15376/biores.10.2.2360-2375
Mosse, W. K. J., Boger, D. V., and Garnier, G. (2012). “Avoiding slip in pulp suspension rheometry,” J. Rheol. 56, 1517-1533. DOI: 10.1122/1.4752193
Mueller, S., Llewellin, E. W., and Mader, H. M. (2010). “The rheology of suspensions of solid particles,” Proc. R. Soc. London, A 466, 1201-1228. DOI: 10.1098/rspa.2009.0445
Mukherjee, T., Kao, N., Gupta, R. K., Quazi, N., and Bhattacharya, S. (2016). “Evaluating the state of dispersion on cellulosic biopolymer by rheology,” J. Appl. Polymer Sci. 133(12), article no. 43200. DOI: 10.1002/APP.43200
Naderi, A., and Lindström, T. (2015). “Rheological measurements on nanofibrillated cellulose systems: A science in progress,” in: Cellulose and Cellulose Derivatives: Synthesis, Modification and Applications, M. I. H. Mondal (ed.), Nova Science Publishers, New York, pp. 187-204
Naderi, A., and Lindström, T. (2016). “A comparative study of the rheological properties of three different nanofibrillated cellulose systems,” Nordic Pulp Paper Res. J. 31(3), 354-363. DOI: 10.3183/NPPRJ-2016-31-03-p354-363
Naderi, A., Lindstrom, T., Erlandsson, J., Sundstrom, J., and Flodberg, G. (2016a). “A comparative study of the properties of three nanofibrillated cellulose systems that have been produced at about the same energy consumption levels in the mechanical delamination step,” Nordic Pulp Paper Res. J. 31(3), 364-371. DOI: 10.3183/NPPRJ-2016-31-03-p364-371
Naderi, A., Lindstrom, T., and Pettersson, T. (2014a). “The state of carboxymethylated nanofibrils after homogenization-aided dilution from concentrated suspensions: A rheological perspective,” Cellulose 21(4), 2357-2368. DOI: 10.1007/s10570-014-0329-9
Naderi, A., Lindstrom, T., and Sundstrom, J. (2014b). “Carboxymethylated nanofibrillated cellulose: Rheological studies,” Cellulose 21(3), 1561-1571. DOI: 10.1007/s10570-014-0192-8
Naderi, A., Lindstrom, T., and Sundstrom, J. (2015a). “Repeated homogenization, a route for decreasing the energy consumption in the manufacturing process of carboxymethylated nanofibrillated cellulose?” Cellulose 22(2), 1147-1157. DOI: 10.1007/s10570-015-0576-4
Naderi, A., Lindstrom, T., Sundstrom, J., and Flodberg, G. (2015b). “Can redispersible low-charged nanofibrillated cellulose be produced by the addition of carboxymethyl cellulose?” Nordic Pulp Paper Res. J. 30(4), 568-577. DOI: 10.3183/NPPRJ-2015-30-04-p568-577
Naderi, A., Lindstrom, T., Sundstrom, J., Pettersson, T., Flodberg, G., and Erlandsson, J. (2015c). “Microfluidized carboxymethyl cellulose modified pulp: A nanofibrillated cellulose system with some attractive properties,” Cellulose 22(2), 1159-1173. DOI: 10.1007/s10570-015-0577-3
Naderi, A., Lindstrom, T., Weise, C. F., Flodberg, G., Sundstrom, J., Junel, K., Erlandsson, J., and Runebjork, A. (2016b). “Phosphorylated nanofibrillated cellulose: Production and properties,” Nordic Pulp Paper Res. J. 31(1), 20-29. DOI: 10.3183/NPPRJ-2016-31-01-p020-029
Nazari, B., and Bousfield, D. W. (2016). “Cellulose nanofibers influence on properties and processing of paperboard coatings,” Nordic Pulp Paper Res. J. 31(3), 511-520. DOI: 10.3183/NPPRJ-2016-31-03-p511-520
Nazari, B., Kumar, V., Bousfield, D. W., and Toivakka, M. (2016). “Rheology of cellulose nanofibers suspensions: Boundary driven flow,” J. Rheology 60(6), 1151-1159. DOI: 10.1122/1.4960336
Nechyporchuk, O., Belgacem, M. N., and Pignon, F. (2014). “Rheological properties of micro-/nanofibrillated cellulose suspensions: Wall-slip and shear banding phenomena,” Carbohydr. Polym. 112, 432-439. DOI: 10.1016/j.carbpol.2014.05.092
Nechyporchuk, O., Belgacem, M. N., and Pignon, F. (2015). “Concentration effect of TEMPO-oxidized nanofibrillated cellulose aqueous suspensions on the flow instabilities and small-angle X-ray scattering structural characterization,” Cellulose 22(4), 2197-2210. DOI: 10.1007/s10570-015-0640-0
Nechyporchuk, O., Belgacem, M. N., and Pignon, F. (2016). “Current progress in rheology of cellulose nanofibril suspensions,” Biomacromol. 17(7), 2311-2320. DOI: 10.1021/acs.biomac.6b00668
Nelson, K., Retsina, T., Iakovlev, M., van Heiningen, A., Deng, Y. L., Shatkin, J. A., and Mulyadi, A. (2016). “American process: Production of low cost nanocellulose for renewable, advanced materials applications,” in: Materials Research for Manufacturing: An Industrial Perspective of Turning Materials into New Products,” L. D. Madsen and E. B. Svedberg (eds.), Springer Series in Materials Science 224, 267-302. DOI: 10.1007/978-3-319-23419-9_9
Nguyen, T. Q., and Kausch, H.-H. (1992). “Chain extension and degradation in convergent flow,” Polymer 33(12), 2611-2621. DOI: 10.1016/0032-3861(92)91145-R
Nishiyama, Y., Kim, U. J., Kim, D. Y., Katsumata, K. S., May, R. P., and Langan, P. (2003). “Periodic disorder along ramie cellulose microfibrils,” Biomacromol. 4(4), 1013-1017. DOI: 10.1021/bm025772x
Noroozi, N., Grecov, D., and Shafiei-Sabet, S. (2014). “Estimation of viscosity coefficients and rheological functions of nanocrystalline cellulose aqueous suspensions,” Liquid Crystals 41(1), 56-66. DOI: 10.1080/02678292.2013.834081
Oguzlu, H., Danumah, C., and Boluk, Y. (2016). “The role of dilute and semi-dilute cellulose nanocrystal (CNC) suspensions on the rheology of carboxymethyl cellulose (CMC) solutions,” Can. J. Chem. Eng. 94(10), 1841-1847. DOI: 10.1002/cjce.22597
Oguzlu, H., Danumah, C., and Boluk, Y. (2017). “Colloidal behavior of aqueous cellulose nanocrystal suspensions,” Current Opin. Colloid Interface Sci. 29, 49-56. DOI: 10.1016/j.cocis.2017.02.002
Okiyama, A., Motoki, M., and Yamanaka, S. (1993). “Bacterial cellulose. 3. Development of a new form of cellulose,” Food Hydrocolloids 6(6), 493-501. DOI: 10.1016/S0268-005X(09)80073-8
Ono, H., Shimaya, Y., Sato, K., and Hongo, T. (2004). “H-1 spin-spin relaxation time of water and rheological properties of cellulose nanofiber dispersion, transparent cellulose hydrogel (TCG),” Polym. J. 36(9), 684-694. DOI: 10.1295/polymj.36.684
Onsager, L. (1932). “Viscosity and particle shape in colloid solutions,” Phys. Rev. 40, 1028-1038.
Orts, W. J., Godbout, L., Marchessault, R. H., and Revol, J. F. (1995). “Shear-induced alignment of liquid-crystalline suspensions of cellulose microfibrils,” in: Flow-Induced Structure in Polymers, A. I. Nakatani and M. D. Dadmun (eds.), Ch. 23, ACS Symp. Ser. 597, 335-348. DOI: 10.1021/bk-1995-0597.ch023
Orts, W. J., Godbout, L., Marchessault, R. H., and Revol, J. F. (1998). “Enhanced ordering of liquid crystalline suspensions of cellulose microfibrils: A small angle neutron scattering study,” Macromolecules 31(17), 5717-5725. DOI: 10.1021/ma9711452
Osong, S. H., Norgren, S., and Engstrand, P. (2013). “An approach to produce nano-ligno-cellulose from mechanical pulp fine materials,” Nordic Pulp Paper Res. J. 28(4), 472-479. DOI: 10.3183/NPPRJ-2013-28-04-p472-479
Ougiya, H., Hioki, N., Watanabe, K., Morinaga, Y., Yoshinaga, F., and Samejima, M. (1998). “Relationship between the physical properties and surface area of cellulose derived from adsorbates of various molecular sizes,” Biosci. Biotech. Biochem. 62(10), 1880-1884. DOI: 10.1271/bbb.62.1880
Ovarlez, G., Rodts, S., Château, X., and Coussot, P. (2009). “Phenomenology and physical origin of shear localization and shear banding in complex fluids,” Rheol. Acta 48, 831-844. DOI: 10.1007/s00397-008-0344-6
Pääkkö, M., Ankerfors, M., Kosonen, H., Nykanen, A., Ahola, S., Österberg, M., Ruokolainen, J., Laine, J., Larsson, P. T., Ikkala, O., et al. (2007). “Enzymatic hydrolysis combined with mechanical shearing and high-pressure homogenization for nanoscale cellulose fibrils and strong gels,” Biomacromolecules 8(6), 1934-1941. DOI: 10.1021/bm061215p
Pääkkönen, T., Dimic-Misic, K., Orelma, H., Pönni, R., Vuorinen, T., and Maloney, T. (2016). “Effect of xylan in hardwood pulp on the reaction rate of TEMPO-mediated oxidation and the rheology of the final nanofibrillated cellulose gel,” Cellulose 23(1), 277-293. DOI: 10.1007/s10570-015-0824-7
Pahimanolis, N., Hippi, U., Johansson, L. S., Saarinen, T., Houbenov, N., Ruokolainen, J., and Seppala, J. (2011). “Surface functionalization of nanofibrillated cellulose using click-chemistry approach in aqueous media,” Cellulose 18(5), 1201-1212. DOI: 10.1007/s10570-011-9573-4
Pal, L., Tyagi, P., and Hubbe, M. A. (2017). “Effects of montmorillonite, kaolinite, protein, and AKD on nanocellulose-based barrier coating packaging,” TAPPI PaperCon 2017, Minneapolis, MN
Parker, J. D. (1972). “The sheet forming process,” TAPPI STAP Ser. 9, TAPPI Press, New York.
Paximada, P., Dimitrakopoulou, E. A., Tsouko, E., Koutinas, A. A., Fasseas, C., and Mandala, I. G. (2016). “Structural modification of bacterial cellulose fibrils under ultrasonic irradiation,” Carbohydr. Polym. 150, 5-12. DOI: 10.1016/j.carbpol.2016.04.125
Peltonen, L., and Hirvonen, J. (2010). “Pharmaceutical nanocrystals by nanomilling: Critical process parameters, particle fracturing and stabilization methods,” J. Pharmacy Pharmacology 62(11), 1569-1579. DOI: 10.1111/j.2042-7158.2010.01022.x
Peng, Y. C., Gardner, D. J., and Han, Y. S. (2012). “Drying cellulose nanofibrils: In search of a suitable method,” Cellulose 19(1), 91-102. DOI: 10.1007/s10570-011-9630-z
Pereda, M., Amica, G., Rácz, I., and Marcovich, N. E. (2011). “Structure and properties of nanocomposite films based on sodium caseinate and nanocellulose fibers,” J. Food Eng. 103, 76-83. DOI: 10.1016/j.jfoodeng.2010.10.001
Petrie, C. J. (1999). “The rheology of fibre suspensions,” J. Non-Newtonian Fluid Mech. 87(2-3), 369-402. DOI: 10.1016/S0377-0257(99)00069-5
Petrie, C. J. S. (2006). “Extensional viscosity: A critical discussion,” J. Non-Newtonian Fluid Mechanics 137, 15-23. DOI: 10.1016/j.jnnfm.2006.01.011
Phan-Thien, N. (2016). “Introduction to suspension rheology,” in: Chinesta, F., and Ausias, G. (eds.) Rheology of Non-spherical Particle Suspensions, Elsevier, Ch. 1.
Philipse, A. P., and Wierenga, A. M. (1998). “On the density and structure formation in gels and clusters of colloidal rods and fibers,” Langmuir 14, 49-54. DOI: 10.1021/la9703757
Pommet, M., Juntaro, J., Heng, J. Y., Mantalaris, A., Lee, A. F., Wilson, K., and Bismarck, A. (2008). “Surface modification of natural fibers using bacteria: Depositing bacterial cellulose onto natural fibers to create hierarchical fiber reinforced nanocomposites,” Biomacromolecules 9(6), 1643-1651. DOI: 10.1021/bm800169g
Pönni, R., Vuorinen, T., and Kontturi, E. (2012). “Proposed nano-scale coalescence of cellulose in chemical pulp fibers during technical treatments,” BioResources 7(4), 6077-6108. DOI: 0.15376/biores.7.4.6077-6108
Pryamitsyn, V., and Ganesan, V. (2008). “Screening of hydrodynamic interactions in Brownian rod suspensions,” J. Chem. Phys. 128(13), 134901. DOI: 10.1063/1.2842075
Puisto, A., Illa, X., Mohtaschemi, M., and Alava, M. J. (2012a). “Modeling the viscosity and aggregation of suspensions of highly anisotropic nanoparticles,” Eur. Phys. J. E 35(1), article no. 6. DOI: 10.1140/epje/i2012-12006-1
Puisto, A., Illa, X., Mohtaschemi, M., and Alava, M. (2012b). “Modeling the rheology of nanocellulose suspensions,” Nordic Pulp Paper Res. J. 27(2), 277-281. DOI: 10.3183/NPPRJ-2012-27-02-p277-281
Qi, W. H., Xu, H. N., and Zhang, L. F. (2015). “The aggregation behavior of cellulose micro/nanoparticles in aqueous media,” RSC Advan. 5(12), 8770-8777. DOI: 10.1039/c4ra08844a
Qiao, C. D., Chen, G. X., Zhang, J. L., and Yao, J. S. (2016). “Structure and rheological properties of cellulose nanocrystals suspension,” Food Hydrocolloids 55, 19-25. DOI: 10.1016/j.foodhyd.2015.11.005
Quemada, D. (1982), “Unstable flows of concentrated suspensions,” Lecture Notes in Physics 164, 210-247. DOI: 10.1007/3-540-11581-1_8
Quennouz, N., Hashmi, S. M., Choi, H. S., Kim, J. W., and Osuji, C. O. (2016). “Rheology of cellulose nanofibrils in the presence of surfactants,” Soft Matter 12(1), 157-164. DOI: 10.1039/c5sm01803j
Raghavan, S. R., and Douglas, J. F. (2012). “The conundrum of gel formation by molecular nanofibers, wormlike micelles, and filamentous proteins: Gelation without cross-links?,” Soft Matter 8, 8539-8546. DOI: 10.1039/c2sm25107h
Rahnama, M., Koch, D. L., and Shaqfeh, E. S. (1995). “The effect of hydrodynamic interactions on the orientation distribution in a fiber suspension subject to simple shear flow,” Phys. Fluids 7(3), 487-506. DOI: 10.1063/1.868647
Rantanen, J., Dimic-Misic, K., Pirttiniemi, J., Kuosmanen, P., and Maloney, T. C. (2015). “Forming and dewatering of a microfibrillated cellulose composite paper,” BioResources 10(2), 3492-3506. DOI: 10.15376/biores.10.2.3492-3506
Rautkoski, H., Pajari, H., Koskela, H., Sneck, A., and Moilanen, P. (2015). “Use of cellulose nanofibrils (CNF) in coating colors,” Nordic Pulp Paper Res. J. 30(3), 511-518. DOI: 10.3183/NPPRJ-2015-30-03-p511-518
Rees, A., Powell, L. C., Chinga-Carrasco, G., Gethin, D. T., Syverud, K., Hill, K. E., and Thomas, D. W. (2015). “3D bioprinting of carboxymethylated-periodate oxidized nanocellulose constructs for wound dressing applications,” Biomed. Res. Intl., article no. 925757. DOI: 10.1155/2015/925757
Revol, J. F., Bradford, H., Giasson, J., Marchessault, R. H., and Gray, D. G. (1992). “Helicoidal self-ordering of cellulose microfibrils in aqueous suspension,” Int. J. Biol. Macromol. 14, 170-172. DOI: 10.1016/S0141-8130(05)80008-X
Rezayati Charani, P., Dehghani-Firouzabadi, M., Afra, E., and Shakeri, A. (2013). “Rheological characterization of high concentrated MFC gel from kenaf unbleached pulp,” Cellulose 20(2), 727-740. DOI: 10.1007/s10570-013-9862-1
Rodriguez-Rivero, C., Hilliou, L., Del Valle, E. M. M., and Galan, M. A. (2014). “Rheological characterization of commercial highly viscous alginate solutions in shear and extensional flows,” Rheologica Acta 53(7), 559-570. DOI: 10.1007/s00397-014-0780-4
Roper, J. A. III (1996). “Introduction to the rheology of paper coatings,” Coating Binders Short Course: Course Notes, 23 pp., TAPPI Press, Atlanta.
Rudraraju, V. S., and Wyandt, C. M. (2005a). “Rheological characterization of microcrystalline cellulose/sodiumcarboxymethyl cellulose hydrogels using a controlled stress rheometer: Part I,” Intl. J. Pharmaceutics 292(1-2), 53-61. DOI: 10.1016/j.ijpharm.2004.10.011
Rudraraju, V. S., and Wyandt, C. M. (2005b). “Rheology of microcrystalline cellulose and sodium carboxymethyl cellulose hydrogels using a controlled stress rheometer: Part II,” Int. J. Pharm. 292(1-2), 63-73. DOI: 10.1016/j.ijpharm.2004.10.012
Russel, W. B. (1978). “Rheology of suspensions of charged rigid spheres,” Journal of Fluid Mechanics 85, 209-232. DOI: 10.1017/S0022112078000609
Russel, W. B. (2009). “Structure-property relations for the rheology of dispersions of charged colloids,” Indust. Eng. Chem. Res. 48(5), 2380-2386. DOI: 10.1021/ie800385m
Saarikoski, E., Rissanen, M., and Seppala, J. (2015). “Effect of rheological properties of dissolved cellulose/microfibrillated cellulose blend suspensions on film forming,” Carbohyd. Polym. 119, 62-70. DOI: 10.1016/j.carbpol.2014.11.033
Saarikoski, E., Saarinen, T., Salmela, J., and Seppala, J. (2012). “Flocculated flow of microfibrillated cellulose water suspensions: An imaging approach for characterisation of rheological behavior,” Cellulose 19(3), 647-659. DOI: 10.1007/s10570-012-9661-0
Saarinen, T., Haavisto, S., Sorvari, A., Salmela, J., and Seppala, J. (2014). “The effect of wall depletion on the rheology of microfibrillated cellulose water suspensions by optical coherence tomography,” Cellulose 21(3), 1261-1275. DOI: 10.1007/s10570-014-0187-5
Saito, T., Nishiyama, Y., Putaux, J. L., Vignon, M., and Isogai, A. (2006). “Homogeneous suspensions of individualized microfibrils from TEMPO-catalyzed oxidation of native cellulose,” Biomacromol. 7(6), 1687-1691. DOI: 10.1021/bm060154s
Salmela, J., Haavisto, S., Koponen, A., Jäsberg, A., and Kataja, M. (2013). “Rheological characterization of micro-fibrillated cellulose fiber suspension using multi scale velocity profile measurements,” Advances in Pulp and Paper Research, 15th Fundamental Research Symposium, Cambridge, England, pp. 495.
Salo, T., Dimic-Misic, K., Gane, P., and Paltakari, J. (2015). “Application of pigmented coating colours containing MFC/NFC: Coating properties and link to rheology,” Nordic Pulp Paper Res. J. 30(1), 165-178. DOI: 10.3183/NPPRJ-2015-30-01-p165-178
Samyn, P., and Taheri, H. (2016). “Rheology of fibrillated cellulose suspensions after surface modification by organic nanoparticle deposits,” J. Mater. Sci. 51(21), 9830-9848. DOI: 10.1007/s10853-016-0216-x
Sandquist, D. (2013). “New horizons for microfibrillated cellulose,” APPITA J. 66(2), 156-162.
Sato, T., and Teramoto, A. (1991). “Dynamics of stiff-chain polymers in isotropic solution: Zero-shear viscosity of rodlike polymers,” Macromolecules 24(1), 193-196. DOI: 10.1021/ma00001a030
Schenker, M., Schoelkopf, J., Mangin, P., and Gane, P. (2016). “Rheological investigation of complex micro and nanofibrillated cellulose (MNFC) suspensions: Discussion of flow curves and gel stability,” TAPPI J. 15(6), 405-416.
Scheuble, N., Geue, T., Kuster, S., Adamcik, J., Mezzenga, R., Windhab, E. J., and Fischer, P. (2016). “Mechanically enhanced liquid interfaces at human body temperature using thermosensitive methylated nanocrystalline cellulose,” Langmuir 32(5), 1396-1404. DOI: 10.1021/acs.langmuir.5b04231
Schlesing, W., Buhk, M., and Osterhold, M. (2004). “Dynamic mechanical analysis in coatings industry,” Prog. Organic Coatings 49(3), 197-208. DOI: 10.1016/j.porgcoat.2003.09.009
Shafiei-Sabet, S., Hamad, W. Y., and Hatzikiriakos, S. G. (2012). “Rheology of nanocrystalline cellulose aqueous suspensions,” Langmuir 28(49), 17124-17133. DOI: 10.1021/la303380v
Shafiei-Sabet, S., Hamad, W. Y., and Hatzikiriakos, S. G. (2013). “Influence of degree of sulfation on the rheology of cellulose nanocrystal suspensions,” Rheol. Acta 52(8-9), 741-751. DOI: 10.1007/s00397-013-0722-6
Shafiei-Sabet, S., Hamad, W. Y., Hatzikiriakos, S. G. (2014). “Ionic strength effects on the microstructure and shear rheology of cellulose nanocrystal suspensions,” Cellulose 21(5), 3347-3359. DOI: 10.1007/s10570-014-0407-z
Shafiei-Sabet, S., Martinez, M., and Olson, J. (2016). “Shear rheology of micro-fibrillar cellulose aqueous suspensions,” Cellulose 23(5), 2943-2953. DOI: 10.1007/s10570-016-1040-9
Shao, Y., Chaussy, D., Grosseau, P., and Beneventi, D. (2015). “Use of microfibrillated cellulose/lignosulfonate blends as carbon precursors: Impact of hydrogel rheology on 3D printing,” Indust. Eng. Chem. Res. 54(43), 10575-10582. DOI: 10.1021/acs.iecr.5b02763
Sherwood, J. D. (1981). “The primary electro viscous effect in a suspension of rods,” J. Fluid Mech. 111, 347-366. DOI: 10.1017/S0022112081002413
Shi, Z. J., Zang, S. S., Jiang, F., Huang, L., Lu, D., Ma, Y. G., and Yang, G. (2012). “In situ nano-assembly of bacterial cellulose-polyaniline composites,” RSC Adv. 2, 1040-1046. DOI: 10.1039/C1RA00719J, Paper
Shi, Z. J., Zang, Y., Phillips, G. O., and Yang, G. (2013). “Utilization of bacterial cellulose in food,” Food Hydrocolloids 35, 539-545. DOI: 10.1016/j.foodhyd.2013.07.012
Shogren, R. L., Peterson, S. C., Evans, K. O., and Kenar, J. A. (2011). “Preparation and characterization of cellulose gels from corn cobs,” Carbohyd. Polym. 86(3), 1351-1357. DOI: 10.1016/j.carbpol.2011.06.035
Siew, C. K., Williams, P. A., and Young, N. W. G. (2005). “New insights into the mechanism of gelation of alginate and pectin: Charge annihilation and reversal mechanism,” Biomacromol. 6(2), 963-969. DOI: 10.1021/bm049341l
Sim, K., Lee, J., Lee, H., and Youn, H. J. (2015). “Flocculation behavior of cellulose nanofibrils under different salt conditions and its impact on network strength and dewatering ability,” Cellulose 22(6), 3689-3700. DOI: 10.1007/s10570-015-0784-y
Simha, R. (1940). “The influence of Brownian movement on the viscosity of solutions,” J. Phys. Chem. 44(1), 25-34. DOI: 10.1021/j150397a004
Siqueira, G., Kokkinis, D., Libaroni, R., Hausmann, M. K., Gladman, A. S., Neels, A., Tingaut, P., Zimmermann, T., Lewis, J. A., and Studart, A. R. (2017). “Cellulose nanocrystal inks for 3D printing of textured cellular architectures,” Adv. Funct. Mater. 2017, article 1604619. DOI: 10.1002/adfm.201604619
Siro, I., and Plackett, D. (2010). “Microfibrillated cellulose and new nanocomposite materials: A review,” Cellulose 17(3), 459-494. DOI: 10.1007/s10570-010-9405-y
Small, A. C., Johnston, J. H., and Clark, N. (2010). “Inkjet printing of water ‘soluble’ doped ZnS quantum dots,” Eur. J. Inorg. Chem. 2010(2), 242-247. DOI: 10.1002/ejic.200900871
Solomon, M. J., and Spicer, P. T. (2010). “Microstructural regimes of colloidal rod suspensions, gels, and glasses,” Soft Matter 6(7), 1391-1400. DOI: 10.1039/b918281k
Sorvari, A., Saarinen, T., Haavisto, S., Salmela, J., Vuoriluoto, M., and Seppala, J. (2014). “Modifying the flocculation of microfibrillated cellulose suspensions by soluble polysaccharides under conditions unfavorable to adsorption,” Carbohydr. Polym. 106, 283-292. DOI: 10.1016/j.carbpol.2014.02.032
Sridhar, I., Johnson, K. L., and Fleck, N. A. (1997). “Adhesion mechanics of the surface force apparatus,” J. Phys. D. – Appl. Phys. 30(12), 1710-1719. DOI: 10.1088/0022-3727/30/12/004
Stone, J. E., and Scallan, A. M. (1966). “Influence of drying on the pore structures of the cell wall,” in: Consolidation of the Paper Web, Trans. Symp. at Cambridge, 1975, F. Bolam (ed.), Tech. Section British Paper & Board Makers Assoc., London, pp. 145-174.
Strazdins, E. (1989). “Theoretical and practical aspects of alum use in papermaking,” Nordic Pulp Paper Res. J. 4(2), 128-134. DOI: 10.3183/NPPRJ-1989-04-02-p128-134
Ström, G., and Kunnas, A. (1991). “The effect of cationic polymers on the water retention value of various pulps,” Nordic Pulp Paper Res. J. 6(1), 12-19. DOI: 10.3183/NPPRJ-1991-06-01-p012-019
Studart, A. R., Amstad, E., and Gauckler, L. J. (2007). “Colloidal stabilization of nanoparticles in concentrated suspensions,” Langmuir 23(3), 1081-1090. DOI: 10.1021/la062042s
Subramanian, R., Kononov, A., Kang, T., Paltakari, J., and Paulapuro, H. (2008). “Structure and properties of some natural cellulosic fibrils,” BioResources 3(1), 192-203. DOI: 10.15376/biores.3.1.192-203
Sultan, S., Sequeira, G., Zimmermann, T., and Mathew, A. P. (2017). “3D printing of nano-cellulosic biomaterials for medical applications,” Current Opin. Biomed. Eng. 2, 29-34. DOI: 10.1016/j.cobme.2017.06.002
Sun, X. X., Wu, Q. L., Lee, S., Qing, Y., and Wu, Y. Q. (2016). “Cellulose nanofibers as a modifier for rheology, curing and mechanical performance of oil well cement,” Sci. Reports (6), article no. 31654. DOI: 10.1038/srep31654
Swerin, A. (1998). “Rheological properties of cellulosic fibre suspensions flocculated by cationic polyacrylamides,” Colloids and Surface A 133, 279-294. DOI: 10.1016/S0927-7757(97)00212-4
Swerin, A., Powell, R. L., and Ödberg, L. (1992). “Linear and nonlinear dynamic viscoelasticity of pulp fiber suspensions,” Nordic Pulp and Paper Research Journal 7(3), 126-132. DOI: 10.3183/NPPRJ-1992-07-03-p 126-132
Switzer, L. H., and Klingenberg, D. J. (2003). “Rheology of sheared flexible fiber suspensions via fiber-level simulations,” J. Rheol. 47, 759-778. DOI: 10.1122/1.1566034
Taheri, H., and Samyn, P. (2016). “Effect of homogenization (microfluidization) process parameters in mechanical production of micro- and nanofibrillated cellulose on its rheological and morphological properties,” Cellulose 23(2), 1221-1238. DOI: 10.1007/s10570-016-0866-5
Takahashi, C., Ishimaru, Y., Iida, I., and Furuta, Y. (2006). “The creep of wood destabilized by change in moisture content. Part 3: The influence of changing moisture history on creep behavior,” Holzforschung 60(3), 299-303. DOI: 10.1515/HF.2006.048
Tanaka, R., Saito, T., Hanninen, T., Ono, Y., Hakalahti, M., Tammelin, T., and Isogai, A. (2016). “Viscoelastic properties of core-shell-structured, hemicellulose-rich nanofibrillated cellulose in dispersion and wet-film states,” Biomacromol. 17(6), 2104-2111. DOI: 10.1021/acs.biomac.6b00316
Tanaka, R., Saito, T., Hondo, H., and Isogai, A. (2015). “Influence of flexibility and dimensions of nanocelluloses on the flow properties of their aqueous dispersions,” Biomacromol. 16(7), 2127-2131. DOI: 10.1021/acs.biomac.5b00539
Tanaka, R., Saito, T., Ishii, D., and Isogai, A. (2014). “Determination of nanocellulose fibril length by shear viscosity measurement,” Cellulose 21(3), 1581-1589. DOI: 10.1007/s10570-014-0196-4
Tang, A. M., Liu, Y., Wang, Q. W., Chen, R. S., Liu, W. Y., Fang, Z. Q., and Wang, L. S. (2016). “A new photoelectric ink based on nanocellulose/CdS quantum dots for screen-printing,” Carbohydr. Polym. 148, 29-35. DOI: 10.1016/j.carbpol.2016.04.034
Tang, Y. J., Yang, S. J., Zhang, N., and Zhang, J. H. (2014). “Preparation and charac-terization of nanocrystalline cellulose via low-intensity ultrasonic-assisted sulfuric acid hydrolysis,” Cellulose 21(1), 335-346. DOI: 10.1007/s10570-013-0158-2
Tatsumi, D. (2007). “Rheology of cellulose fiber disperse systems and cellulose solutions,” Nihon Reoroji Gakkaishi 35(5), 251-256. DOI: 10.1678/rheology.35.251
Tatsumi, D., Ishioka, S., and Matsumoto, T. (1999). “Effect of particle and salt concentrations on the rheological properties of cellulose fibrous suspensions,” Nihon Reoroji Gakkaishi 27(4), 243-248. DOI: 10.1678/rheology.27.243
Tatsumi, D., Kourogi, H., Chen, B., and Matsumoto, T. (2008). “Effect of natural additives on the rheological properties of cellulose fiber disperse systems,” Colloids and Surfaces A—Physicochemical and Engineering Aspects 316(1–3), 151-158. DOI: 10.1016/j.colsurfa.2007.09.001
Tomczak, A., Jelonek, T., and Jakubowski, M. (2012). “Changes in the structure and properties of wood as an effect of the impact of wind on trees,” Sylwan 156(10), 776-783.
Tsalagkas, D., Dimic-Misic, K., Gane, P., Rojas, O. J., Maloney, T., and Csoka, L. (2015). “Rheological behavior of sonochemically prepared bacterial cellulose aqueous dispersions,” SIE Conference, Belgrade, Conference Proceedings
Ueno, T., Yokota, S., Kitaoka, T., and Wariishi, H. (2007). “Conformational changes in single carboxymethylcellulose chains on a highly oriented pyrolytic graphite surface under different salt conditions,” Carbohydrate Res. 342(7), 954-960. DOI: 10.1016/j.carres.2007.01.017
Ureña-Benavides, E. E., Ao, G. Y., Davis, V. A., and Kitchens, C. L. (2011). “Rheology and phase behavior of lyotropic cellulose nanocrystal suspensions,” Macromol. 44(22), 8990-8998. DOI: 10.1021/ma201649f
Usov, I., Nyström, G., Adamcik, J., Handschin, S., Schütz, C., Fall, A., Bergström, L., and Mezzenga, R. (2015). “Understanding nanocellulose chirality and structure-properties relationship at the single fibril level,” Nature Communications 6, article no. 7564. DOI:10.1038/ncomms8564
van de Ven, T. G. M., and Sheikhi, A. (2016). “Hairy cellulose nanocrystalloids: A novel class of nanocellulose,” Nanoscale 8(33), 15101-15114. DOI: 10.1039/c6nr01570k
Varanasi, S., He, R. L., and Batchelor, W. (2013). “Estimation of cellulose nanofibre aspect ratio from measurements of fibre suspension gel point,” Cellulose 20(4), 1885-1896. DOI: 10.1007/s10570-013-9972-9
Veen, S. J., Versluis, P., Kuijk, A., and Velikov, K. P. (2015). “Microstructure and rheology of microfibril-polymer networks,” Soft Matter 11(46), 8907-8912. DOI: 10.1039/c5sm02086g
Vesterinen, A. H., Myllytie, P., Laine, J., and Seppala, J. (2010). “The effect of water-soluble polymers on rheology of microfibrillar cellulose suspension and dynamic mechanical properties of paper sheet,” J. Appl. Polym. Sci. 116(5), 2990-2997. DOI: 10.1002/app.31832
Walz, J. Y. (1998). “The effect of surface heterogeneities on colloidal forces,” Advan. Colloid Interface Sci. 74, 119-168. DOI: 10.1016/S0001-8686(97)00042-0
Wang, H. D., Jessop, P. G., Bouchard, J., Champagne, P., and Cunningham, M. F. (2015). “Cellulose nanocrystals with CO2-switchable aggregation and redispersion properties,” Cellulose 22(5), 3105-3116. DOI: 10.1007/s10570-015-0690-3
Wang, H. K., Zhang, X. X., Jiang, Z. H., Yu, Z. X., and Yu, Y. (2016). “Isolating nanocellulose fibrils from bamboo parenchymal cells with high intensity ultrasonication,” Holzforschung 70(5), 401-409. DOI: 10.1515/hf-2015-0114
Weise, U. (1998). “Hornification – Mechanisms and terminology,” Paperi Puu – Paper & Timber 80(2), 110-115.
Wierenga, A. M., and Philipse, A. P. (1998). “Low-shear viscosity of isotropic dispersions of (Brownian) rods and fibres; A review of theory and experiments,” Colloids and Surfaces A: Physicochemical and Engineering Aspects 137, 355-372. DOI: 10.1016/S0927-7757(97)00262-8
Winuprasith, T., and Suphantharika, M. (2013). “Microfibrillated cellulose from mangosteen (Garcinia mangostana L.) rind: Preparation, characterization, and evaluation as an emulsion stabilizer,” Food Hydrocolloids 32(2), 383-394. DOI: 10.1016/j.foodhyd.2013.01.023
Wu, Q., Li, X. W., Fu, S. Y., Li, Q., and Wang, S. Q. (2017). “Estimation of aspect ratio of cellulose nanocrystals by viscosity measurement: Influence of surface charge density and NaCl concentration,” Cellulose 24(8), 3255-3264. DOI: 10.1007/s10570-017-1341-7
Wu, Q., Meng, Y. J., Wang, S. Q., Li, Y. J., Fu, S. Y., Ma, L. F., and Harper, D. (2014). “Rheological behavior of cellulose nanocrystal suspension: Influence of concentration and aspect ratio,” J. Appl. Polym. Sci. 131(15), article no. 40525. DOI: 10.1002/app.40525
Xia, Z. Y., Patchan, M., Maranchi, J., and Trexler, M. (2015). “Structure and relaxation in cellulose hydrogels,” J. Appl. Polymer Sci. 132(24), article no. 42071. DOI: 10.1002/app.42071
Xu, X. Z., Liu, F., Jiang, L., Zhu, J. Y., Haagenson, D., and Wiesenborn, D. P. (2013). “Cellulose nanocrystals vs. cellulose nanofibrils: A comparative study on their microstructures and effects as polymer reinforcing agents,” ACS Appl. Mater. Interfaces 5(8), 2999-3009. DOI: 10.1021/am302624t
Xu, Y., Atrens, A. D., and Stokes, J. R. (2017). “Rheology and microstructure of aqueous suspensions of nanocrystalline cellulose rods,” J. Colloid Interface Sci. 496, 130-140. DOI: 10.1016/j.jcis.2017.02.020
Xu, Y. X., Kuang, Y. D., Salminen, P., and Chen, G. (2016). “The influence of nano-fibrillated cellulose as a coating component in paper coating,” BioResources 11(2), 4342-4352. DOI: 10.15376/biores.11.2.4342-4352
Yang, J., Han, C. R., Duan, J. F., Xu, F., and Sun, R. C. (2013). “Mechanical and viscoelastic properties of cellulose nanocrystals reinforced poly(ethylene glycol) nanocomposite hydrogels,” ACS Appl Mater Interfaces 5, 3199-3207. DOI: 10.1021/am4001997
Yang, S. J., Tang, Y. J., Wang, J. M., Kong, F. G., and Zhang, J. H. (2014). “Surface treatment of cellulosic paper with starch-based composites reinforced with nanocrystalline cellulose,” Indust. Eng. Chem. Res. 53(36), 13980-13988. DOI: 10.1021/ie502125s
Yang, X. H., and Zhu, W. L. (2007). “Viscosity properties of sodium carboxymethyl cellulose solutions,” Cellulose 14(5), 409-417. DOI: 10.1007/s10570-007-9137-9
Zauscher, S., and Klingenberg, D. J. (2000). “Surface and friction forces between cellulose surfaces measured with colloidal probe microscopy,” Nord. Pulp Pap. Res. J. 15(5), 459-468. DOI: 10.3183/NPPRJ-2000-15-05-p459-468
Zepic, V., Fabjan, E. S., Kasunic, M., Korosec, R. C., Hancic, A., Oven, P., Perse, L. S., and Poljansek, I. (2014). “Morphological, thermal, and structural aspects of dried and redispersed nanofibrillated cellulose (NFC),” Holzforschungg 68(6), 657-667. DOI: 10.1515/hf-2013-0132
Zhang, J. H., Song, H. N., Lin, L., Zhuang, J. P., Pang, C. S., and Liu, S. J. (2012). “Microfibrillated cellulose from bamboo pulp and its properties,” Biomass Bioenergy 39, 78-83. DOI: 10.1016/j.biombioe.2010.06.013
Zhang, X. X., Yu, Y., Li, W. J., Ren, D., and Wang, H. K. (2015). “An efficient dispersive agent – KCl for ultrasonic preparation of microfibrillated cellulose (MFC),” BioResources 10(4), 6635-6642. DOI: 10.15376/biores.10.4.6635-6642
Zhong, L., Fu, S., Peng, X., Zhan, H., and Sun, R. (2012). “Colloidal stability of negatively charged cellulose nanocrystalline in aqueous systems,” Carbohydr. Polym. 90(1), 644-649. DOI: 10.1016/j.carbpol.2012.05.091
Zhou, D. D., Tang, Y. J., Zhang, N., Zhang, J. H., and Liu, D. D. (2014). “Effect of various cellulose derivatives on the properties of pigment coatings: A comparative study,” Digest J. Nanomater. Biostruc. 9(1), 305-315.
Zhu, Y., Luo, X. G., Wu, X., Li, W., Li, B., Lu, A., and Liu, S. L. (2017). “Cellulose gel dispersions: Fascinating green particles for the stabilization of oil/water Pickering emulsion,” Cellulose 24(1), 207-217. DOI: 10.1007/s10570-016-1093-9
Zimmermann, T., Bordeanu, N., and Strub, E. (2010). “Properties of nanofibrillated cellulose from different raw materials and its reinforcement potential,” Carbohydr. Polym. 79(4), 1086-1093. DOI: 10.1016/j.carbpol.2009.10.045
Zimmermann, T., Pöhler, E., and Geiger, T. (2004). “Cellulose fibrils for polymer reinforcement,” Adv. Eng. Mater. 6, 754-761. DOI: 10.1002/adem.200400097
Zoppe, J. O., Osterberg, M., Venditti, R. A., Laine, J., and Rojas, O. J. (2011). “Surface interaction forces of cellulose nanocrystals grafted with thermoresponsive polymer brushes,” Biomacromol. 12(7), 2788-2796. DOI: 10.1021/bm200551p
DOI: 10.15376/biores.12.4.Hubbe
APPENDIX
Table A. Compilation of Key Parameters from Publications Dealing with Nanocellulose Aqueous Suspensions
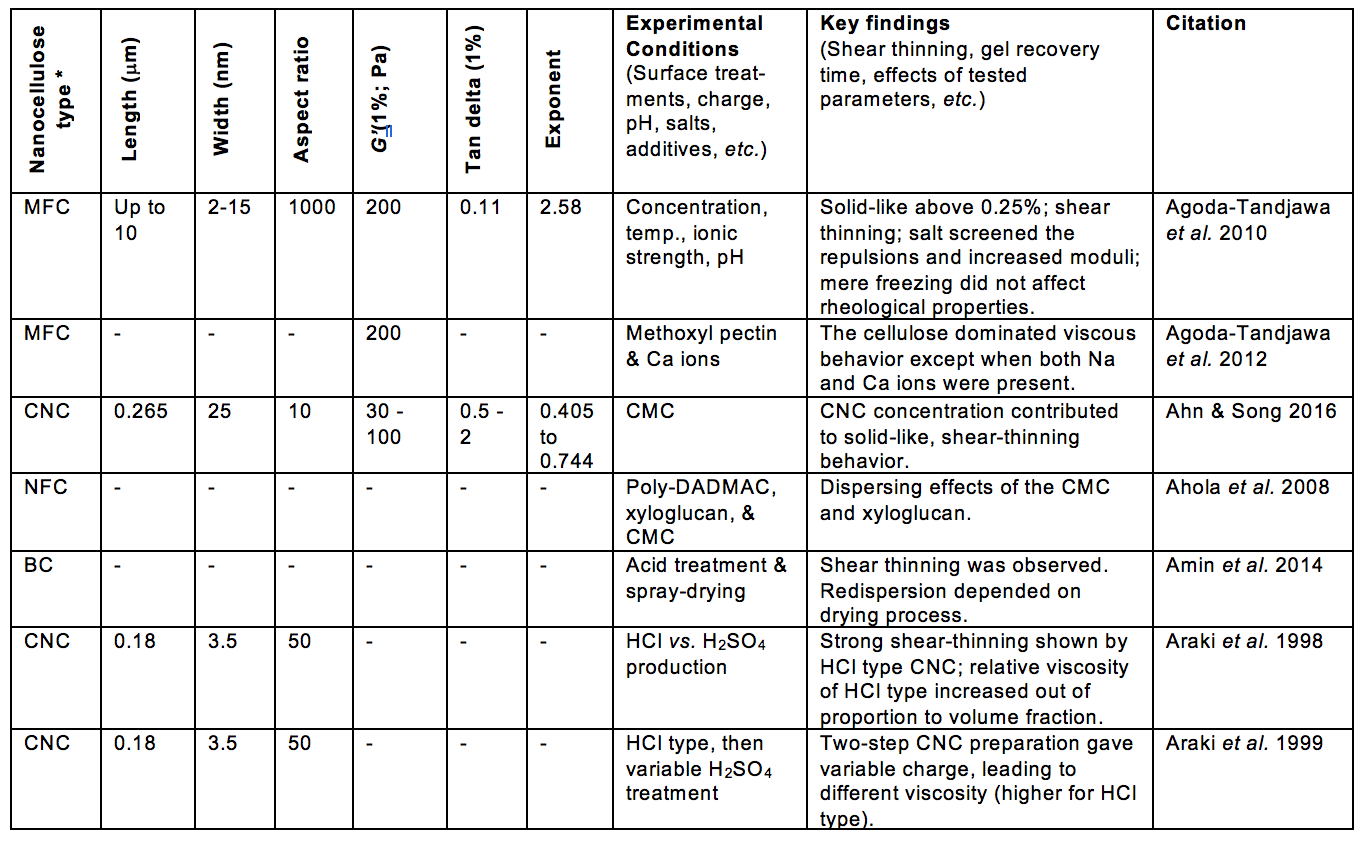
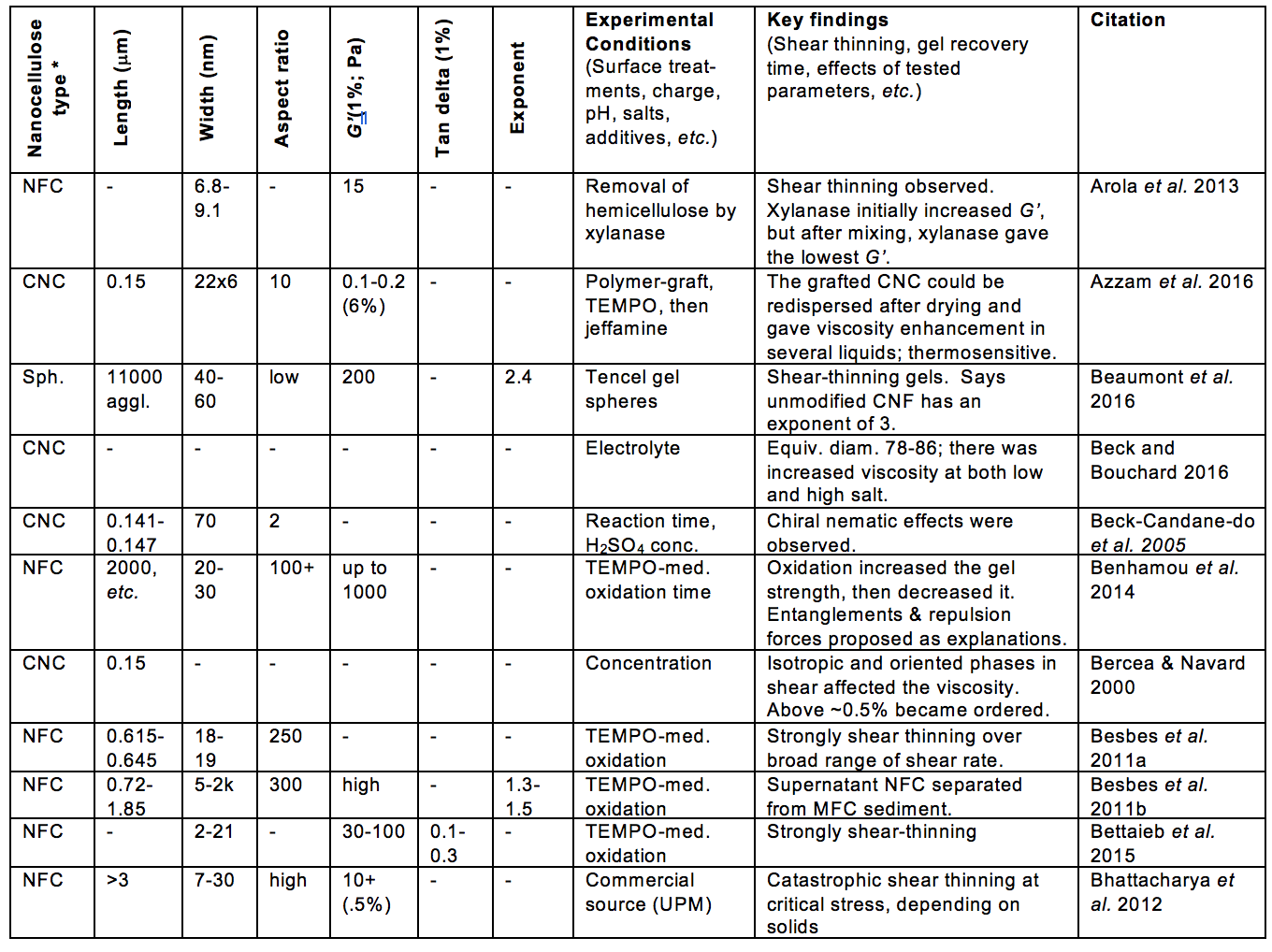
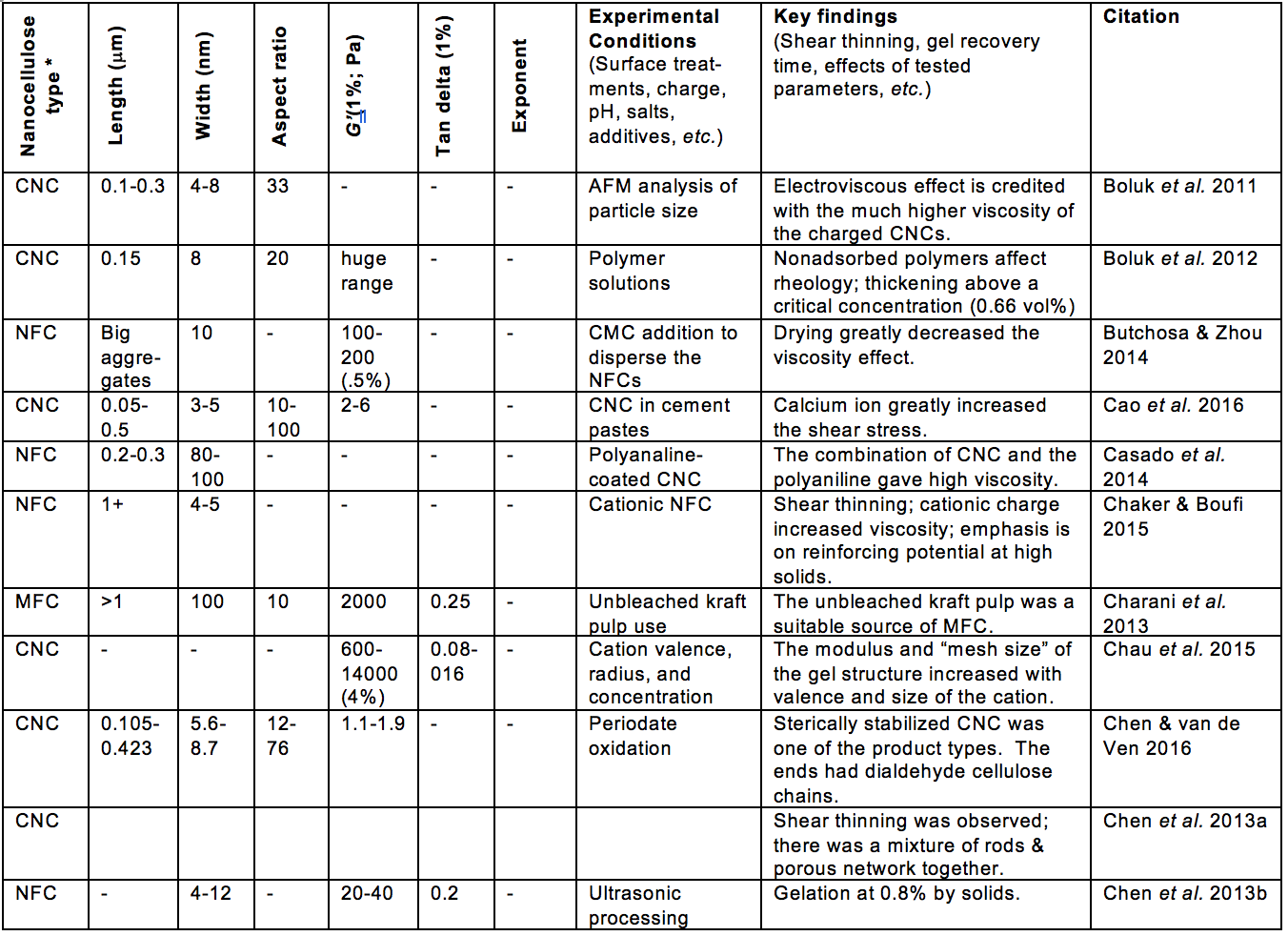
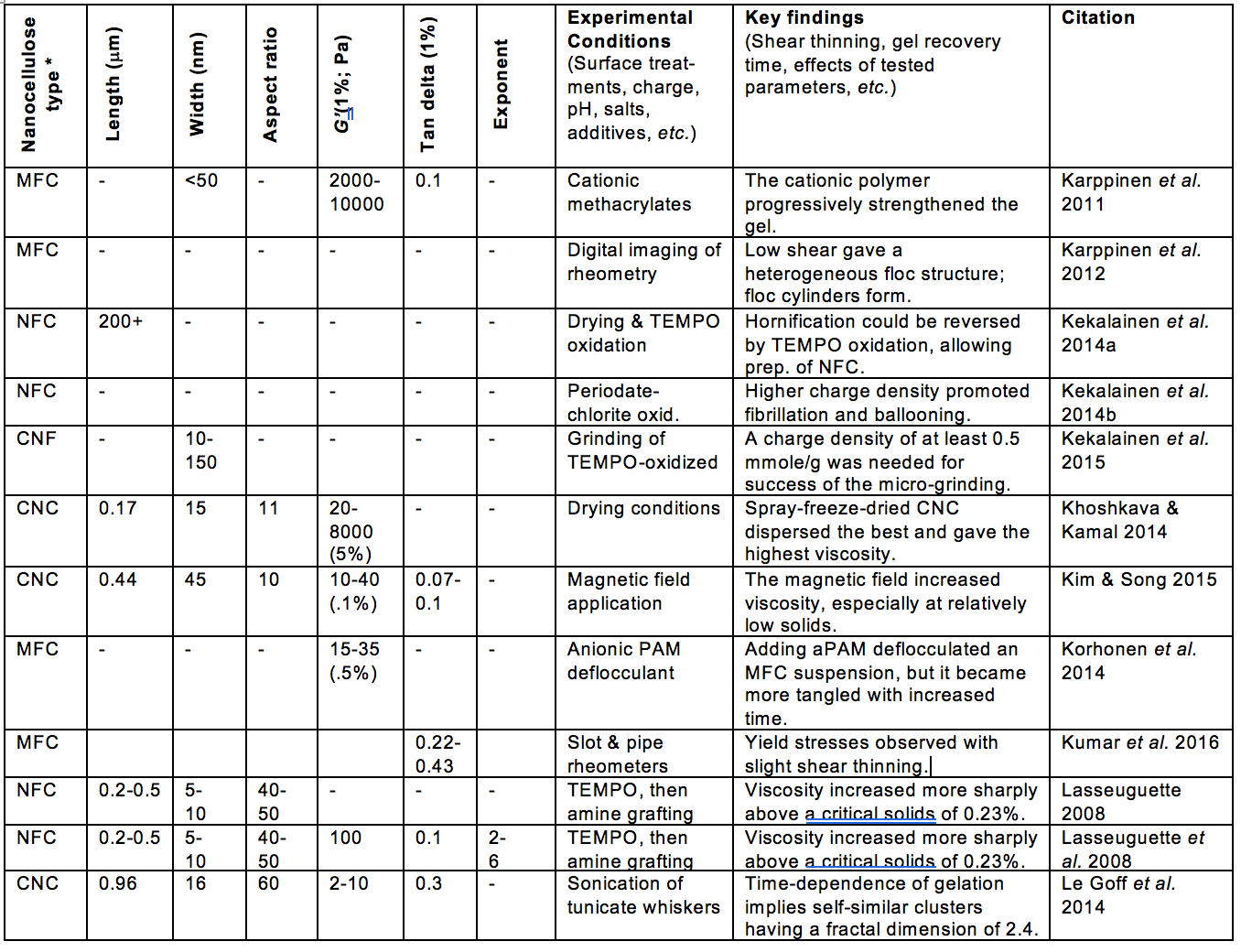
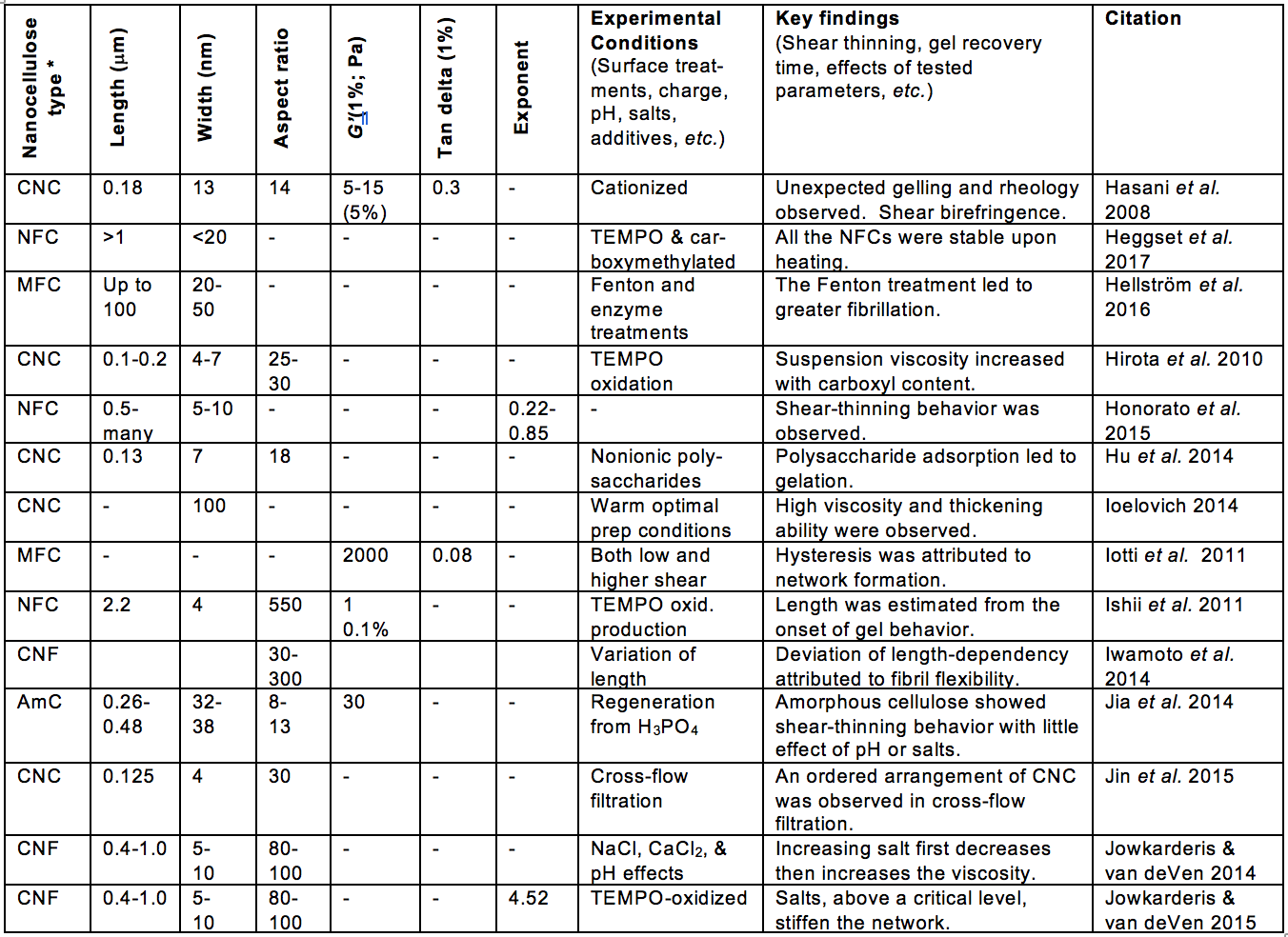
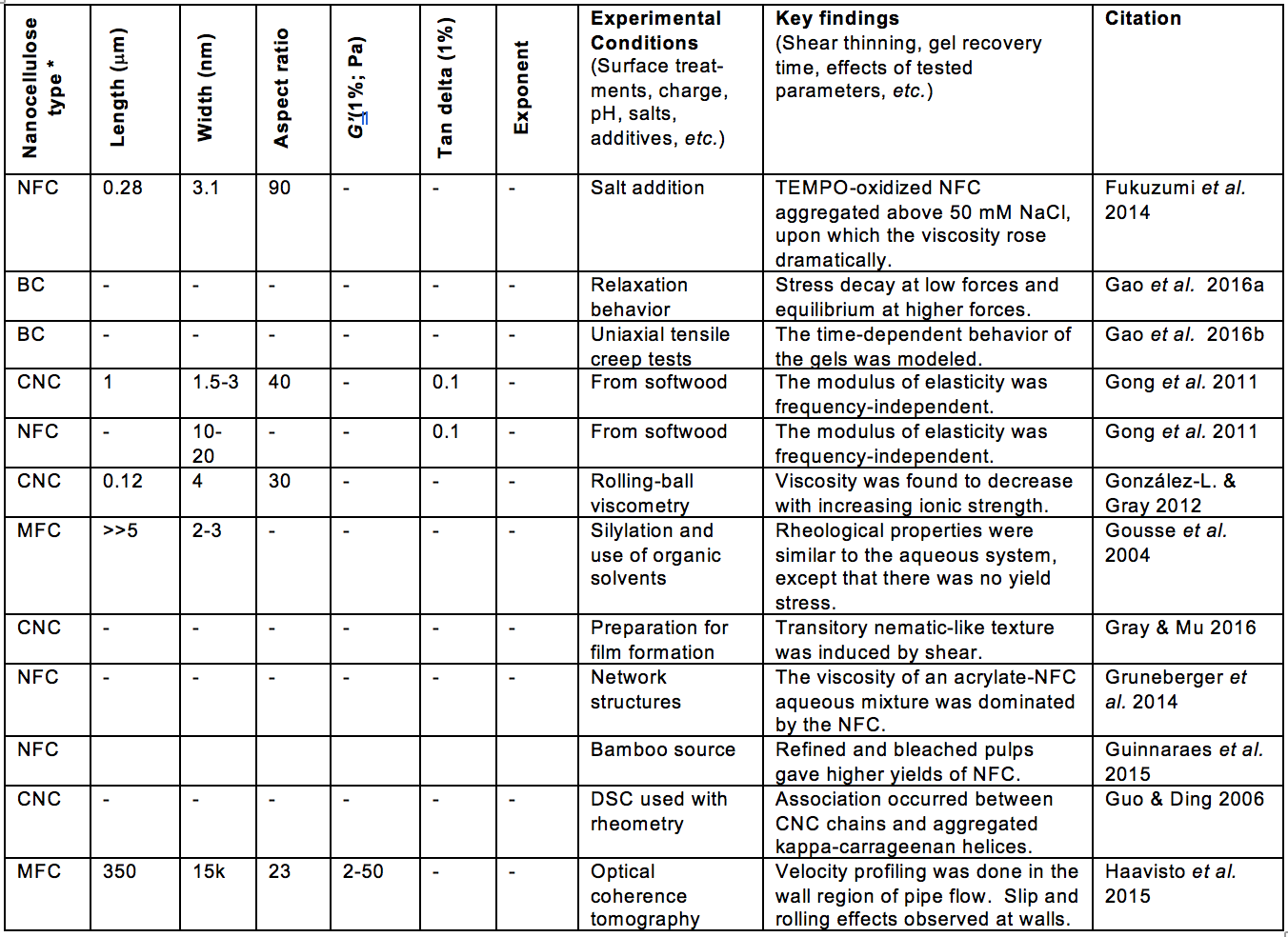
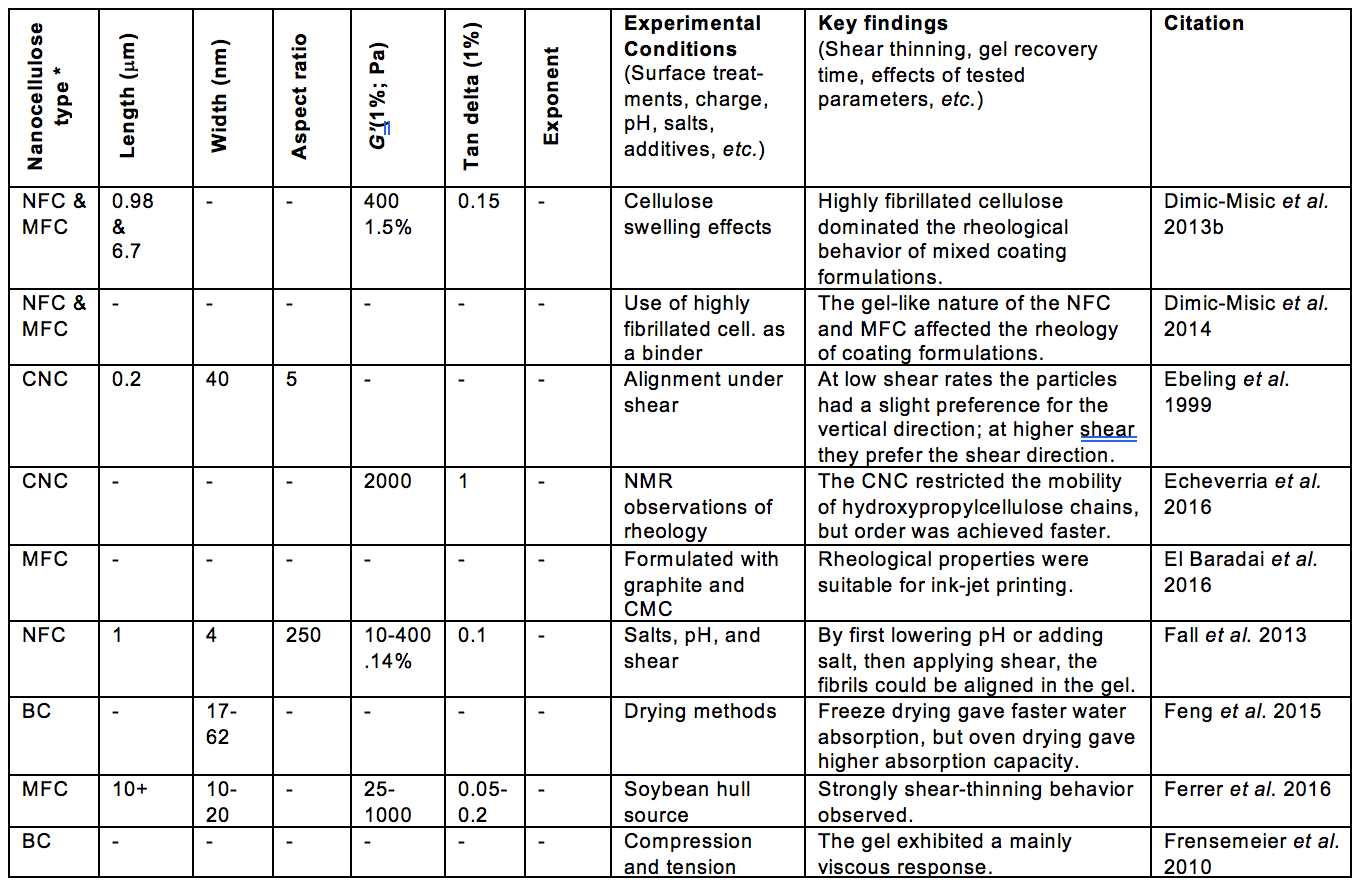
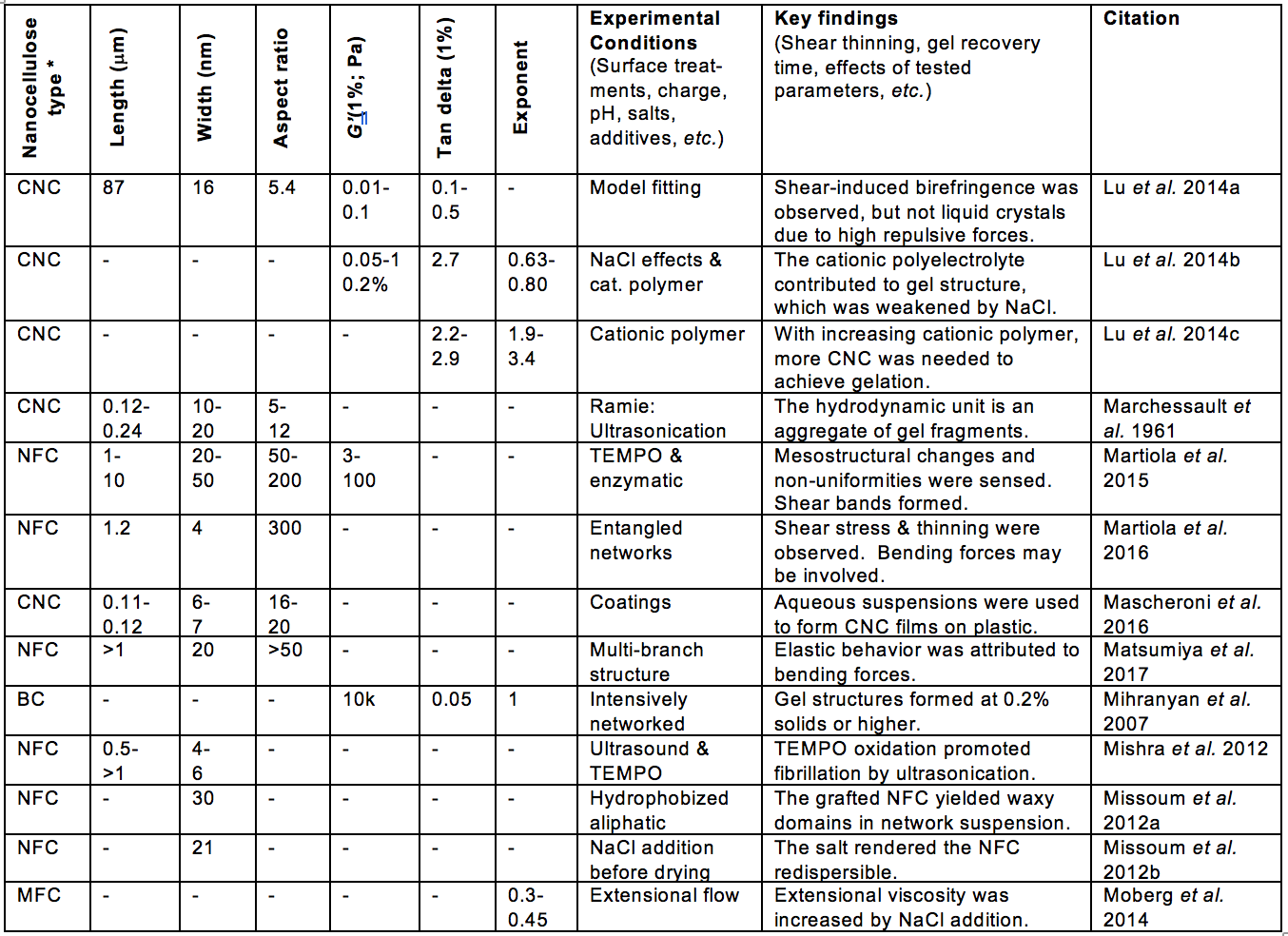
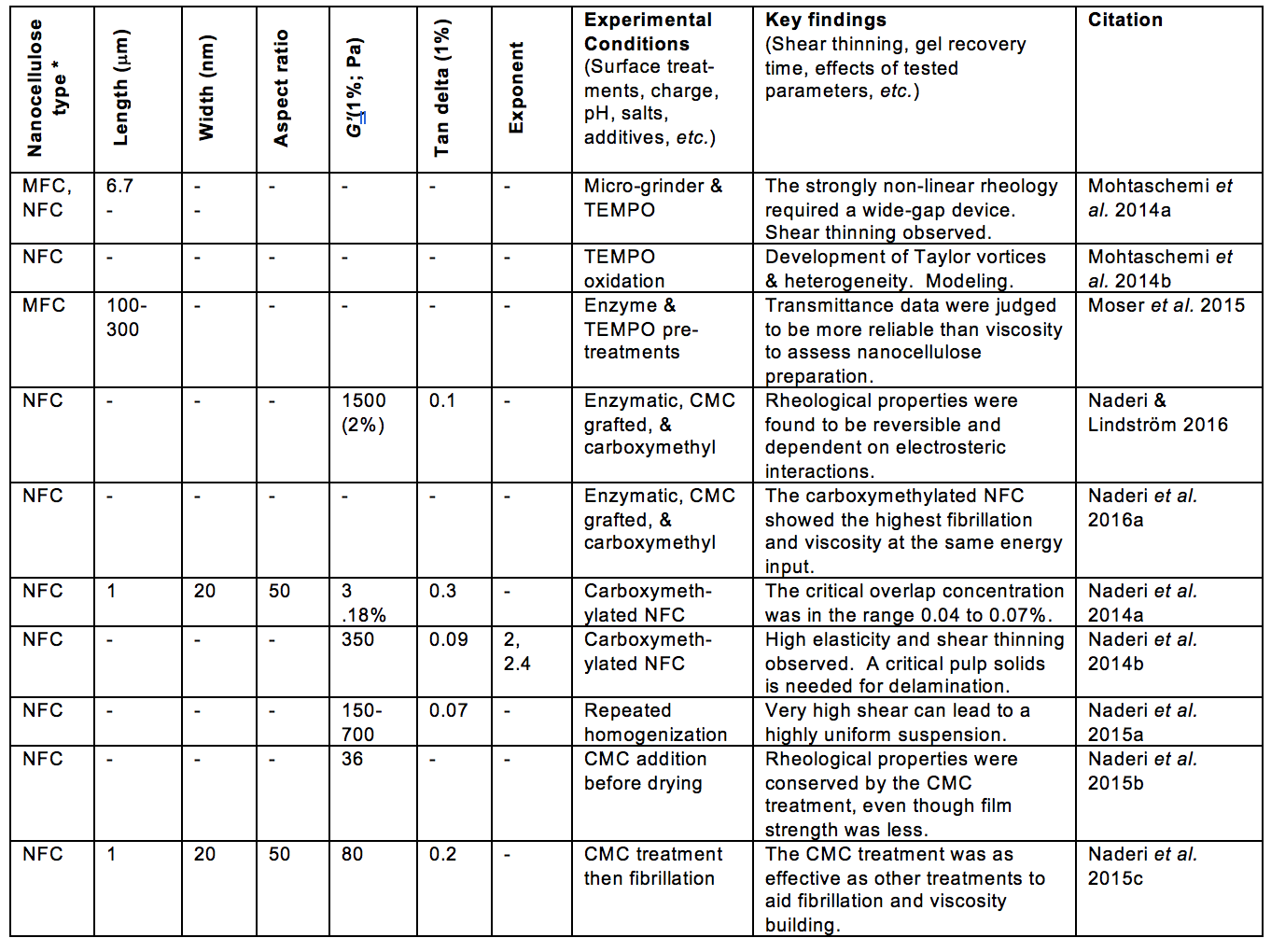
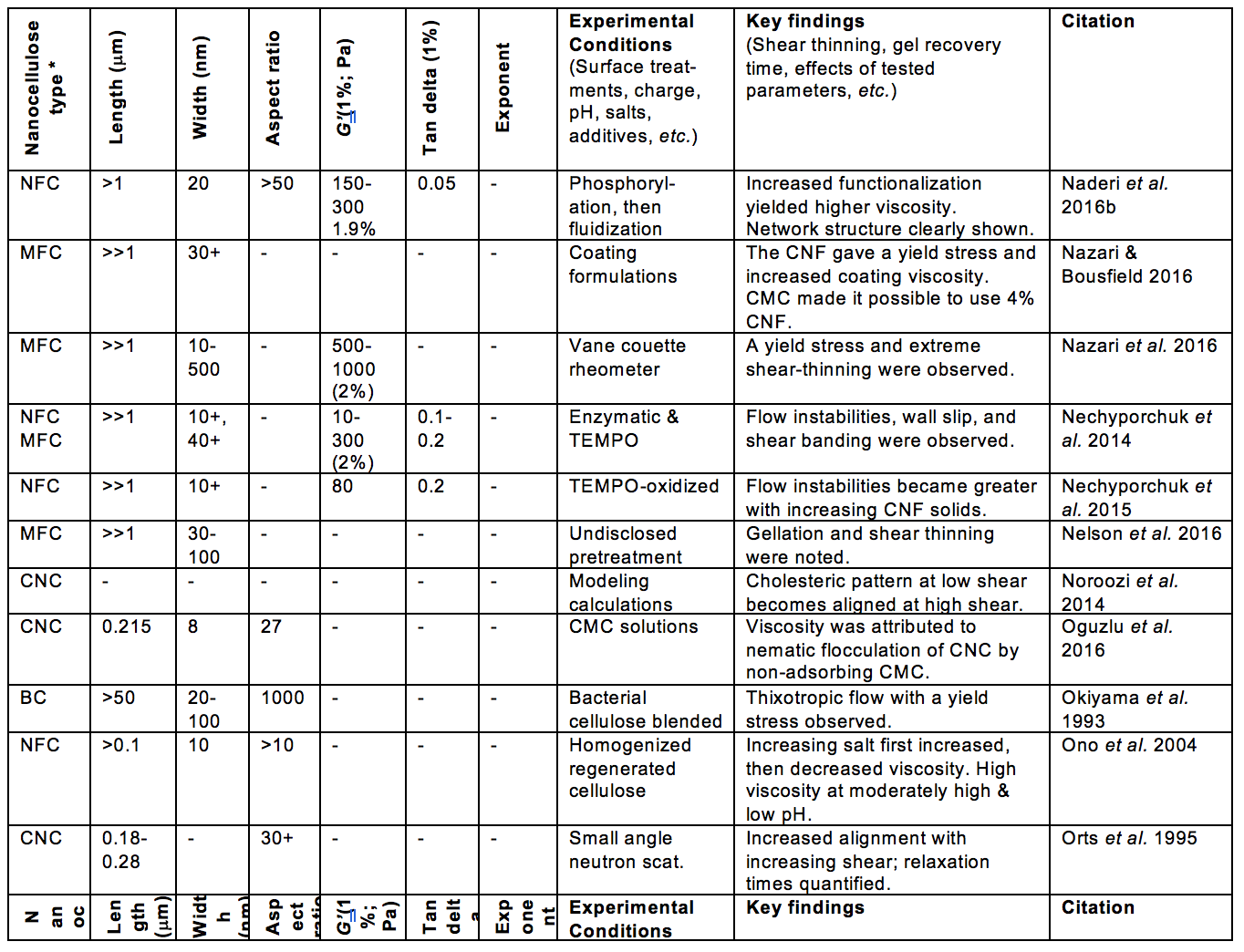
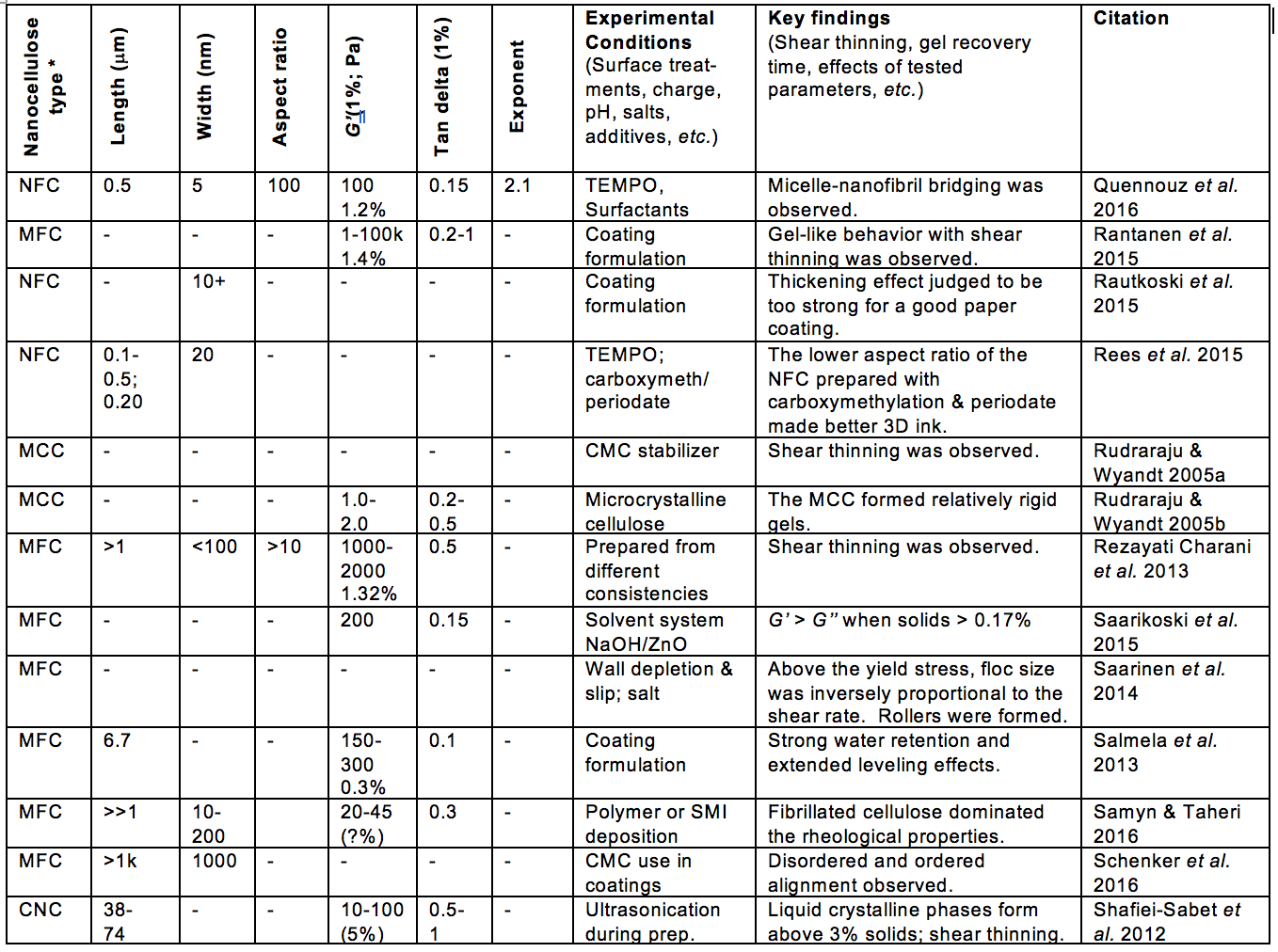
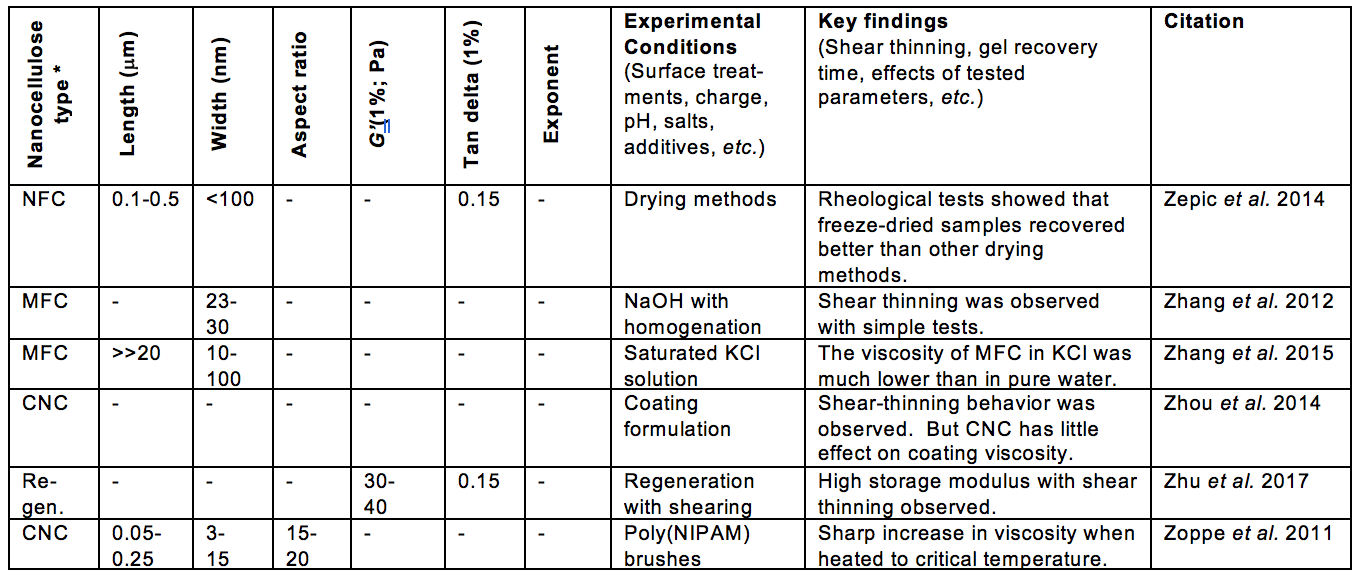 12
12
Key: AmC = amorphous cellulose;
BC = bacterial cellulose (in most cases having been subjected to mechanical shearing);
CNC = cellulose nanocrystals (made by breaking down amorphous regions, often by sulfuric acid digestion);
CNF = cellulose nanofibrils (essentially no branches or networks, e.g. by cellulase and/or TEMPO oxidation);
MFC = microfibrillated cellulose (sheared; highly fibrillated cellulosic fibers, but can be larger than NFC);
NFC = nanofibrillated cellulose (sheared; fibril diameter less than 100 nm and length less than 100 mm);
Regen. = regenerated cellulose;
Sph = spherical cellulose particles
Note: In the columns for storage modulus, G’, and tan delta, the default is to show the value corresponding to a 1% solids suspension; if such data were available only at another solids, that solids level is shown (as percent).
The “Exponent” refers to the equation, hr = , where the reduced viscosity is a function of the volume fraction of solids, raised to a power.
