Measurement of the Poisson’s ratio of materials based on the bending mode of the cantilever plate

Abstract

Principles and methods to dynamically test the Poisson’s ratio of isotropic material and timber are proposed in this work. Five species of lumbers were processed into cantilever plates of tangential, radial, and cross sections with different length-width ratios of 6, 5, 4, and 3. The “Shell 63” element in ANSYS software was adopted to calculate strain and stress under the first-order bending mode. The paste position of the strain rosette for the Poisson’s ratio of timber was obtained through strain-stress relationship and regression analysis under states of stress, strain analysis, and plane stress. This method was also applied to steel, aluminum, and glass. For both isotropic and orthotropic materials such as timber, the paste positions of the strain rosette were determined by the position where transverse stress within the plate was zero during the first-order bending vibration. Meanwhile, the lateral and longitudinal strains of the spectrum were measured using the transient excitation method. In the spectrum, the ratio of linear amplitude between the lateral and longitudinal strain of the first-order bending frequency was taken as the measured value of the Poisson’s ratio of the material. The accuracy of the results was verified by axial tension and static four-point bending tests.

Full Article

Measurement of the Poisson’s Ratio of Materials Based on the Bending Mode of the Cantilever Plate

Zizhen Gao,^a Xian Zhang,^a Yunlu Wang,^a Renchen Yang,^a Ganggang Wang,^b and Zheng Wang ^a,*

Principles and methods to dynamically test the Poisson’s ratio of isotropic material and timber are proposed in this work. Five species of lumbers were processed into cantilever plates of tangential, radial, and cross sections with different length-width ratios of 6, 5, 4, and 3. The “Shell 63” element in ANSYS software was adopted to calculate strain and stress under the first-order bending mode. The paste position of the strain rosette for the Poisson’s ratio of timber was obtained through strain-stress relationship and regression analysis under states of stress, strain analysis, and plane stress. This method was also applied to steel, aluminum, and glass. For both isotropic and orthotropic materials such as timber, the paste positions of the strain rosette were determined by the position where transverse stress within the plate was zero during the first-order bending vibration. Meanwhile, the lateral and longitudinal strains of the spectrum were measured using the transient excitation method. In the spectrum, the ratio of linear amplitude between the lateral and longitudinal strain of the first-order bending frequency was taken as the measured value of the Poisson’s ratio of the material. The accuracy of the results was verified by axial tension and static four-point bending tests.

Keywords: Cantilever plate; First-order bending mode; Stress; Strain; Poisson’s ratio

Contact information: a: College of Materials Science and Engineering and b: College of Mechatronics Engineering, Nanjing Forestry University, Nanjing, Jiangsu 210037 China;

* Corresponding author: wangzheng63258@163.com

INTRODUCTION

Timber is an orthotropic material. The elastic constants in the main direction are E_L, E_R, E_T, G_LR, G_LT, G_RT, µ_LR, µ_RT, µ_RL, µ_TL, and µ_TR. Among the six Poisson’s ratios, only three of them are independent, specifically µ_LR, µ_LT, and µ_RT (or µ_TR); the other three can be calculated based on the forward elastic modulus and the aforementioned Poisson’s ratios through the symmetry of the flexibility matrix. Therefore, there are nine independent elastic constants for timber—three each for elastic modulus, shear moduli, and Poisson’s ratio (Sun 1999; Tan and Zhou 2007). Poisson’s ratio is defined as the absolute value of the ratio between transverse strain and longitudinal strain in the linear segment of the axial tension (compression) curve (Liu 1983).

From the perspective of definition, the specimen for testing Poisson’s ratio should be under unidirectional stress, and the corresponding strain should be in the linear segment of the tensile curve. Generally, axial compression is often applied to the static test of the Poisson’s ratio of timber, with specimen sizes of 20 mm × 20 mm × 30 mm, 20 mm × 20 mm × 50 mm, or 30 mm × 30 mm × 60 mm. If the Poisson’s ratio of the cantilever plate is measured based on the first-order bending mode, there is a transverse normal stress (σ_y) in addition to the normal stress (σ_x) during its first-order bending vibration. In other words, internal stress is not an uneven biaxial plane stress during the first-order bending vibration of the cantilever plate. Furthermore, there is a difference of constant factor between stress and strain at each point during the modal vibration of the plate. However, the given value of stress or strain itself has no engineering meaning.

According to the stress and strain analysis of the cantilever plate in the first-order bending mode, the transverse stress (σ_y) in the plate is very small. It even monotonically decreases from a positive to a negative value along the centerline of the plate, which means there is a position (x₀) where σ_y = 0. In other words, there is an area where the cantilever plate is under uniaxial stress during the first-order bending vibration of the cantilever plate, in accordance with the definition of Poisson’s ratio. Furthermore, during the modal vibration of the plate, there is a difference of constant factor among the stresses of various points, which does not hinder the measurement of the Poisson’s ratio because it is the ratio of transverse strain to longitudinal strain. Therefore, the constant factor is eliminated during the calculation of Poisson’s ratio. It is thus feasible to measure Poisson’s ratio by pasting the strain gauge at the appropriate position based on the first-order bending mode of the cantilever plate (Fu 2002). It should be noted that the transverse stress (σ_y) should not be ignored, even if it is very small, because there is a significant difference among the three elastic moduli of timber. The correct measured value of Poisson’s ratio can only be obtained when the strain rosette is at the position of σ_y = 0.

In 2015, Wang (2015) dynamically measured the Poisson’s ratios along the grain of the radial section (µ_LR), across the grain on the radial section (µ_RL), and across the grain on the transverse section (µ_RT) of timber. In 1996, Ma (1996) studied the distribution of the 0° uniaxial fiber-composite cantilever plate on the center line (–ε_y/ε_x) along the plate length (with length-to-width ratios of 3, 4, and 5) using the difference method (Ma 1996), thus determining Poisson’s ratio. However, the principle of testing µ_LR, µ_LT, and µ_RT was not provided with an overall explanation in the two literatures theoretically.

There are a lot of methods of measuring Poisson’s ratio of materials. For example, there are the mechanical static testing method using two pairs of extensometers, the acoustic method using stimulated Brillouin scattering (SBS), surface acoustic wave (SAW) and acoustic microscopy (AM), the electrometric method, and the optical method based on the theory of photoelastic wave and vibration theory of elastic resonance. However, at present, there have been rather few studies on the Poisson’s ratio of wood. Especially, the dynamic measurement of Poisson’s ratio for viscoelastic materials has not received enough attention. The axial tension or compression is the most commonly used method for statically testing the wood Poisson ratio. Because the method of the axial tension or compression test should be conducted using the material testing machine, there is the problem of loading through the centre. For the axial compression method, the contact condition between the machine clamp and the surface of specimen may also cause problems. Therefore, the measurement of wood Poisson’s ratio by the axial tension or axial compression test has critical requirements that are hard to fulfill. Besides, it is difficult to get high accuracy, and the resulting Poisson’s ratio values are prone to showing a large dispersion. In this work, the method of dynamic testing of wood Poisson’s ratio according to the first-order bending mode of the cantilever plate is proposed. This approach can quickly determine the position to paste the strain rosette and has advantages of swiftness, convenience, high accuracy, and good repeatability. In addition, the testing data has low dispersion. The position to paste strain rosette for dynamic measurement of Poisson’s ratio in tangential section _LT is related to wood density and width-to-length ratio of the cantilever plate; the position to paste strain rosette for dynamic measurement of Poisson’s ratio in radial section _LR and in cross section _RT are only related to width-to-length ratio of the cantilever plate. The frequency spectrums of lateral and longitudinal strain of the strain rosette were obtained by transient excitation method. The value of Poisson’s ratio by dynamic test is the ratio between linear spectral amplitudes of transverse and longitudinal strains under the first-order bending frequency. Poisson’s ratios in the tangential and radial sections of Pinus tabulaeformis, in the radial and cross sections of Sitka spruce, Mongolian oak, and others were measured by dynamic tests. Then the correctness of it was verified by static tests.

Particularly, Functional Gradient Material (FGM) and nanowire are both advanced materials with function of use, adaption to the environment, and controllability. They represent the development direction of material science in this century. Over the years, a lot of research work has been conducted on FGM from three aspects: material design, manufacture, and performance evaluation. Indeed, many innovative achievements have been obtained, but the mechanical properties still remains in the period of theoretical prediction. In addition, there are quite a few papers about experimentally measuring elastic constants of FGM and nanowire materials. Thereinto, the theory of hyperbolic sine shear deformation was applied to analyzing static bending and free vibration of FGM (Hebali et al. 2014). In another paper (Bouderba et al. 2013), the theory of trigonometric shear deformation was applied to describing the distribution of transverse shear stress and predicting the thermomechanical bending response of functionally graded plates for FGM. Currently, nanomaterials still remain in the step of computational analysis by finite element theory. In our work, finite element calculation and experimental tests are combined. This idea and method can be applied to the dynamic measurement and analysis of Poisson’s ratio of novel materials, such as FGM and nanowires.

In this work, the principle and method for dynamically testing the Poisson’s ratio of timber were explained based on the stress-strain physical relationship (Hooke’s Law) and the stress-strain analysis of the cantilever plate in the first-order bending mode. Furthermore, the accuracy of the testing results was verified using a static test.

Furthermore, the principle and method of testing the Poisson’s ratio of timber were also applied to isotropic materials. The position of the strain rosette used to measure Poisson’s ratio was also obtained from the dynamic testing of the isotropic materials. The results showed that the Poisson’s ratios of the materials (e.g., steel, rolled aluminum, and copper) according to both the dynamic and static tests corresponded to the code values. This work applies to the measurement of Poisson’s ratio for both metals and nonmetals isotropic materials, and wood which is a heterogeneous and anisotropic natural polymer material.

EXPERIMENTAL

Dynamic and static tests were conducted to measure the Poisson’s ratios of timber and isotropic materials. The static test was aimed at verifying the correctness of dynamic test.

Method of Pasting the Strain Rosette and Bridge Connection

Specimens from the tangential section (LT), radial section (LR), and transverse section (RT) were made according to the L, R, and T directions of timber. Based on the length-to-width ratios (or width-to-length ratios) of the cantilever plate, the positions of the strain rosette were calculated according to Eqs. 3, 4, and 5. Both the upper and lower sides of the plate were pasted with a cross strain rosette at the calculated position. The testing results showed that the ratios of lateral strain to longitudinal strain for the upper and lower sides of the plate using a quarter bridge connection were not always the same. Sometimes the difference was significant, which indicates the variation of performance along the thickness of the plate. To improve the accuracy of the measurement, the transverse and longitudinal strain gauges of the upper and lower sides were connected in the half-bridge for mutual compensation in measuring Poisson’s ratio. For isotropic materials, only one cross strain rosette should be pasted on both the upper or lower sides of the cantilever plate, namely the quarter-bridge connection.

Experimental Flow Chart

Figure 2 shows the flow chart of measuring the dynamic Poisson’s ratio. Data were collected from two channels. Channel 1 was connected to the longitudinal strain gauge, and Channel 2 was connected to the transversal strain gauge. The specimen was excited at the position near the free end of the centerline to do free vibration. Based on the first-order bending frequency of the cantilever specimen, a low-pass filter was first applied for filtering out the second and higher orders of frequencies (Wang 2007). The collected data were processed using Nanjing Analyzer (Nanjing Analyzer Software Engineering Co., Ltd.; Nanjing, China) with SsCRAS software (vibration and dynamic signal acquisition analysis system) for spectrum analysis (Brancheriau and Bailleres 2002; Wang et al. 2008). The amplitudes of the linear spectrum of the lateral and longitudinal strain of the first-order bending frequency can be seen in Fig. 1. The ratio of amplitude between the transverse and longitudinal strains was the measured value of Poisson’s ratio. Each test was conducted three times. The average of the amplitude ratio between the transverse and longitudinal strain was taken to be the dynamically measured value of the specimen’s Poisson’s ratio.

Fig. 1. Flow chart of measuring Poisson’s ratio using the transient excitation dynamic test

RESULTS AND DISCUSSION

Figure 2 shows the frequency spectrum of Mongolian Oak specimen No. 4 (Wang et al. 2008; Wang et al. 2012). Through the calculation of the amplitude ratios between the transverse and longitudinal strain at the first-order bending frequency, the Poisson’s ratio was calculated to be 0.577.

Figure 3 shows the waveform of Mongolian Oak specimen No. 4. Channel 1 represents the waveform of the longitudinal strain, and Channel 2 represents the waveform of the transverse strain. The waveforms of the longitudinal and transverse strains are in reverse, with a phase difference of 180°; they differed by a negative sign.

Fig. 2. Frequency spectrum of Mongolian Oak specimen No. 4

Fig. 3. Waveforms of the longitudinal and transverse strains of Mongolian Oak specimen No. 4

According to the waveform of Mongolian Oak specimen No. 4, the Poisson’s ratio was calculated to be 0.578 based on the average ratio of the peak values of transverse to longitudinal dynamic strains. This result indicates that the measured values of Poisson’s ratio are the same whether they were calculated from the time domain (peak-to-peak value of waveform) or from the frequency domain (amplitude of the linear spectrum at the first-order bending frequency of the frequency spectrum). Therefore, the dynamically measured value of Poisson’s ratio was obtained from the frequency spectrum.

Dynamic Measurement of Poisson’s Ratio for Timber

Dynamic measurement of Poisson’s ratios µ_LT and µ_LR for Chinese pine

The size of the Chinese pine specimen was 300 mm × 60 mm × 12.2 mm, with a clamping length of 60 mm; thus a cantilever plate of l/b = 4 was realized. There were five specimens each for both the radial and tangential sections. The position of the strain rosette on the radial section was x₀ = 0.544l, determined by Eq. 4; the position of the strain rosette on the tangential section was x₀ = 0.567l, determined by Eq. 3. Air-dry density was calculated with an average of 0.472 g/cm³.

Fig. 4. Frequency spectrums of the longitudinal and transverse strains of tangential-section Chinese Pine specimen No. 6

Table 1. Dynamic Testing Values of µ_LR and µ_LT of Chinese Pine

The measured values of the dynamic Poisson’s ratio µ_LR on the radial section for Chinese pine were as follows: mean value of 0.41, standard deviation of 0.032, and variation coefficient of 7.8%. The measured values of the dynamic Poisson’s ratio µ_LT on the tangential section of Chinese Pine were as follows: mean of 0.48, standard deviation of 0.040, and variation coefficient of 8.4%.

Dynamic measurement of the Poisson’s ratio µ_LR of Sitka spruce

The size of the radial-section specimen of Sitka spruce was 625 mm × 107 mm × 12.2 mm, with a clamping length of 60 mm. Thus, a cantilever specimen of l/b = 4.5 was realized, and the number of specimens was 11. When l/b = 4.5, the position of the strain rosette on the radial section was x₀= 0.52l, according to Eq. 4.

Fig. 5. Frequency spectrums of the longitudinal and transverse strains of radial-section Sitka spruce specimen No. XJ7

Table 2. Dynamic Testing Values of µ_LR of Sitka Spruce

The measured values of the dynamic Poisson’s ratio µ_LR of the radial section of Sitka spruce were as follows: mean value of 0.40, standard deviation of 0.033, and variation coefficient of 8.1%.

Dynamic measurement of the Poisson’s ratio (µ_RT) of Sitka spruce

The cross-section specimen of Sitka spruce measured 220 mm × 60 mm × 12.2 mm, with a clamping length of 40 mm. Thus, a cantilever specimen of l/b = 3 was realized, and the number of specimens was four. As l/b = 3, the position of the strain rosette on the radial section should be x₀= 0.5 l, according to Eq. 5.

Fig. 6. Frequency spectrums of the longitudinal and transverse strains of the cross-section of Sitka Spruce specimen No. 2

Table 3. Dynamic Testing Values of the µ_RT of Sitka Spruce

The measured values of the dynamic Poisson’s ratio µ_LR of Sitka spruce on the cross section were as follows: mean value of 0.57, standard deviation of 0.042, and variation coefficient of 7.4%.

Dynamic measurement of the Poisson’s ratio of Mongolian oak

Table 4. Dynamic Testing Values of the Poisson’s Ratio of Mongolian Oak

The size of the specimen was 710 mm × 130 mm × 18 mm, with a clamping depth of 60 mm, and 10 specimens were prepared. The cantilever plate had dimensions of 650 mm × 130 mm × 18 mm and l/b = 5, with an average air-dry density of 800 kg/m³.

The along-the-grain specimen of Mongolian oak, obtained from the floor blank without notches, was not a single radial-section or tangential-section specimen. For the specimen of Mongolian oak with ρ = 800 kg/m³ of l/b = 5, the positions of the strain rosette were all x₀ = 0.5l according to Eqs. 3 and 4.

The measured values of the dynamic Poisson’s ratio of Mongolian oak were as follows: mean value of 0.48, standard deviation of 0.073, and variation coefficient of 15.2%.

Static Measurement of Poisson’s Ratio for Timber

Measurement of the Poisson’s ratio by the axial tension test

First, three pieces of lumber with nominal sizes of 300 mm × 40 mm × 12.2 mm that were sawn from a large board of Sitka Spruce with a width of 107 mm were taken as specimens in the dynamic test (the same specimen numbers were selected).

The measurement set-up consisted of the following:

● YD-28A type dynamic strain gauges (East China Electronic Instrument; Shanghai, China);

● BX120-5AA type Strain Gauge with resistance of 120 ohms, sensitivity factor of 2.08 ± 1% and length and width of 5 mm and 3 mm (Beijing Yiyang Strain and Vibration Testing Technology Co., Ltd.; Beijing, China)

● One Nanjing Analyzer AZ308R-type Signal Collection Box (Nanjing Analyzer Software Engineering Co., Ltd.; Nanjing, China);

● One SANS100KN-300KN Universal Mechanical Testing Machine. (Shenzhen Sans Material Test Instrument Co., Ltd.; Shenzhen, China).

Before testing, each side of the specimen was pasted with a strain rosette. Longitudinal and transverse gauges on both sides were connected in the series to eliminate the bending strain caused by improper loading during the stretching process. The outputs of the longitudinal and transverse gauges of the strain rosette were connected to Channels 1 and 2, respectively, of the signal collection box by the quarter-bridge method. SsCRAS software was used to record the longitudinal and transverse strains. During testing, the test machine provided continuous loading, with a tensile loading rate of 1 mm/min. The recorded values of the longitudinal and transverse strains were within a loading range between the lower limit of 2 kN and the upper limit of 3.5 kN. In data processing, the text file of the signal collection box recorded the values of the longitudinal and transverse strains under loads from the lower to upper limits. Then, several groups of values were selected to verify their linearity for the determination of Poisson’s ratio based on the slope. Poisson’s ratio was simply calculated according to Eq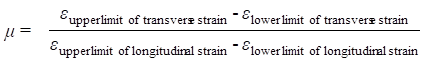. 1:

 (1)

Static measurement of Poisson’s ratio with a four-point bending test

The specimens were selected from those used in the measurement of the dynamic Poisson’s ratio, with the same specimen numbers. The nominal size of the radial section of Chinese pine and Sitka spruce was 300 mm × 12.2 mm × 12.2 mm, with a span of 240 mm and a loading type l/3-l/3-l/3. The nominal size of the transverse section of Sitka spruce was 220 mm × 12.2 mm × 12.2 mm, with a span of 200 mm and a loading type l/4-l/2-l/4.

Table 5. Four-Point Bending and Axial Tension Measurement of the Static Poisson’s Ratio for the Tangential Section of Chinese Pine and the Transverse and Radial Sections of Sitka Spruce

For specimens taken from the radial and tangential sections, the lower limit loading was 4.165 N, and the upper limit loading was 16.66 N (△P = 12.496 N). In terms of the transverse-section specimen, the lower limit loading was 1.0192 N, and the upper limit loading was 2.744 N (△P = 1.7248 N). Furthermore, µ = –Δε_{transverse strain} / Δε_{longitudinal strain}.

Each specimen was tested three times, and the average of the second and third test values was taken as the measured value of the Poisson’s ratio.

Measurement of Poisson’s Ratio for Isotropic Materials

The dynamic and static testing methods of measuring the Poisson’s ratio for timber can be applied to isotropic materials. The only difference was the position to paste strain rosette.

Figure 7 shows the dynamic and static loading methods for measuring the Poisson’s ratio of the cantilever plate made of isotropic materials. The Poisson’s ratio was measured by exciting the cantilever plate to the first-order bending vibration (Wang et al. 2015), while the static Poisson’s ratio was measured by applying a concentrated load at the midpoint of the free end of the cantilever plate to generate static strain.

Fig. 7. Static and dynamic loading methods for measuring the Poisson’s ratio of the cantilever plate

For specimens of steel, rolled aluminum, and rolled pure copper with sizes as indicated in Table 6, positions to paste strain rosette were determined by Eqs. 7 and 8. Testing results are also shown in Table 6.

Table 6. Results of the Dynamic and Static Poisson’s Ratios of Steel, Aluminum, and Copper

According to the data in Table 6, the measured Poisson’s ratios of rolled aluminum and pure copper were within the range of their code values. Furthermore, the Poisson’s ratios obtained from the dynamic and static tests were extremely consistent, with a maximum difference of only 3.5%; the dynamically tested Poisson’s ratio of steel was also in accordance with that of the static test in axial tension, with a difference of only 1.3%. Therefore, the accuracy of the dynamic measurement of Poisson’s ratio for isotropic materials was verified by the axial tension and bending tests.

When the cantilever plate is in bending vibration or static bending, points in the plate are in the condition of biaxial plane stress. According to the stress-strain relationship of isotropic and orthotropic materials under the condition of biaxial stress, in other words, the Hooke’s Law, absolute value of the ratio between transverse and longitudinal strains equals to the Poisson’s ratio only on the points where transverse stress σ_y = 0. To determine the position where σ_y = 0 when the cantilever plate is in first-order bending vibration or static bending, by ANSYS software, the output stress and strain results showed that there is truly a point where σ_y = 0. At this position the absolute value of the ratio between transverse and longitudinal strains equals the input value of Poisson’s ratio in ANSYS. Therefore, the position where σ_y = 0 is where strain rosette should be pasted. At this position, measured absolute value of the ratio between transverse and longitudinal strains can be accepted as measured value of Poisson’s ratio. It is recommended for dynamic measurement of Poisson’s ratio that the ratio between amplitudes of transverse and longitudinal strain in the linear part of first-order bending frequency in the spectrum of cantilever plate should be taken as the measured value of Poisson’s ratio.

The calculation results showed that the positions where σ_y = 0 for dynamic and static tests are different. Its correctness has been verified by dynamic and static tests of steel, rolled aluminum and pure copper (Table 6).

Dynamic tests of Poisson’s ratio for Chinese pine (tangential and radial sections), Sitka spruce (radial and cross sections) and Mongolian oak were conducted according to correct positions to paste strain rosette proposed in this work. To verify the correctness of positions to paste strain rosette, static axial tension tests of Poisson’s ratio for Sitka spruce (radial section) and static four-points bending tests for Chinese Pine (tangential section) and Sitka spruce (cross section) were then conducted. Data in Table 5 indicates that the results from static and dynamic tests were fairly identical according to the mean values. As for data scattering, results from dynamic testing were better than that from static tests. This demonstrates the correctness of dynamic measurement of Poisson’s ratios µ_LT, µ_LR, and µ_RT is verified by static axial tension test and static four-points bending test.

For timber and isotropic materials, principles of dynamic and static measurements of Poisson’s ratio are as follows:

Stress-Strain Relationship of Timber

During the first-order bending vibration, there was biaxial plane stress within the cantilever plate. In terms of the tangential section of the cantilever plate, the relationship between strains ( in the Ldirection and in the T direction) and stresses (σ_L and σ_T) can be expressed as follows:

 (2)

According to the symmetry of the flexibility matrix, it was determined that E_Tµ_LT = E_Lµ_TL. The first subscript letter of µ notes the direction of stretching, and the second letter denotes the direction of shrinkage. Meanwhile, µ_TL denotes the shrinkage along direction L caused by stretching along direction T, specifically

The expressions for σ_L and σ_T were derived from to Eq. 1, such that

 when σ_T = 0,  , namely 

Similarly, through analysis of the relationship between strain (ε_L, ε_R) and stress (σ_L, σ_R) in the directions of L and R, it was found that

 when σ_R = 0, namely 

Based on the above analysis, for tangential-section timber cut along the L and T directions, µ_LTcan be measured by pasting a cross strain rosette at the position of σ_T = 0. For radial sections of timber intercepted along the L and R directions, µ_LR can be measured by pasting the cross strain rosette at the position of σ_R = 0.

For the Poisson’s ratios of the transverse section (µ_RT or µ_TR), the relevant stress-strain relation can be described in Eq. 3,

 (3)

which is solved as,

 , 

when σ_R = 0,  and when σ_T = 0, 

According to the symmetry of the flexibility matrix, it was found that E_Tµ_LT = E_Lµ_TL (on the tangential section); E_Rµ_LR = E_Lµ_TL (on the radial section); and E_Tµ_RT = E_Rµ_TR (on the transverse section). Therefore, there are only three independent Poisson’s ratios: µ_LT, µ_LR, and µ_RT (or µ_TR).

Stress and Strain Analysis of the First-order Bending Mode of the Cantilever Plate

Material constants input in ANSYS calculation

The “Shell 63” element was used for ANSYS calculation, with mesh generations of 60 × 10, 50 × 10, 40 × 10, and 30 × 10 applied to specimens with l/b = 6, 5, 4, and 3, respectively. In the ANSYS calculation, the main-direction elastic constants of the tangential section (Table 1) were input to obtain the positions of the strain rosette pasted for measuring µ_LT.

Table 7. Elastic Constants of Balsa, Spruce, Scots pine, Ash, and Beech (Tangential Section)

In the ANSYS calculation, the relationships between the coordinate axes (x, y, and z) and the timber directions (L, T, and R) were as follows.

On the radial section:  ;

On the tangential section:  (corresponding to data in Table 1);

On the transverse section:  .

The nine elastic constants were input to the radial and transverse sections of timber according to the corresponding relationships between the coordinate axes and timber directions.

Output information of ANSYS calculation

Based on the stress data of the first-order bending mode, σ_y/σ_x was calculated by selecting the σ_xand σ_y of each node on the center line of the plate. Based on the strain data of the first-order bending mode, –ε_y/ε_x and –ε_z/ε_x were calculated by selecting the ε_x, ε_y, and ε_z of each node along the center line of the plate. The results show that –ε_y/ε_x increased with x/l, while –ε_z/ε_x declined with x/l.

After calculation, it was found that –ε_y/ε_x = µ_LT and –ε_z/ε_x = µ_LR were in the same position of x₀ ( ). Furthermore, σ_y/σ_x changed sign at the position of x₀, satisfying σ_y/σ_x = 0. Therefore, according to Testing Principle 1, the absolute value of the ratio between the measured transverse and longitudinal strain is the Poisson’s ratio when the cross strain rosette is pasted at x₀.

For the tangential-section specimens of Scots pine (l/b = 5), the σ_y/σ_x vs.–ε_y/ε_x curve was plotted based on the stress and strain data of the first-order bending mode calculated using the ANSYS modal program (Fig. 8). At the position of x₀ determined by σ_y/σ_x = 0, the value of –ε_y/ε_x was exactly equal to the value of µ_LT for Scots Pine. Figure 1 shows that x₀ = 0.5286l ~ 0.53l.

Fig. 8. Position of the strain rosette pasted for measuring the Poisson’s ratio of Scots pine (l/b = 5)

Position of the strain rosette pasted for measuring the µ_LT, µ_LR, and µ_RT of timber

Table 1 shows the cantilever plates of the five tree species. From the analysis of stress and strain of the first-order bending mode (20 calculation schemes), the paste positions of the strain rosette for measuring µ_LT were obtained (see Table 2). According to the calculation, the width of the plate was 123 mm, with thicknesses of 8 mm, 12.2 mm, and 18 mm, respectively. Thus, –ε_y/ε_xwas independent of plate thickness.

Table 8. Position of Strain Rosette x/l Pasted for Measuring the µ_LT of Cantilever Plates from Five Tree Species

Based on the data in Table 2, the binary linear regression of x/l (calculated position) for ρ and b/lwere obtained as follows. The paste position of the strain rosette for measuring the µ_LT of the tangential section was obtained according to Eq. (4):

 (4)

 ；  .

Equation 3 was used to calculate the paste positions of the strain rosette for measuring µ_LR and µ_RT, although they are not so correlated as µ_LT and air-dry density ρ. However, they have a close relationship with the length-to-width ratio of the cantilever plate, and the results are shown as follows:

The paste position of the strain rosette for measuring µ_LR on the radial section is:

 (5)

(  , n=4,  ～6).

The paste position of the strain rosette for measuring µ_RT on the transverse section is:

 (6)

(  , n=4,  ～6).

Positions to Paste Strain Rosette for Measurement of Poisson’s Ratio of Isotropic Materials

The principle and method of dynamically measuring the Poisson’s ratio of timber are also applicable for isotropic materials, which was analyzed and verified as follows. For the cantilever plate made of isotropic materials in the first-order bending vibration, relationships between the normal stresses (σ_x and σ_y) and between the line strains (ε_x and ε_y) in the plate were:

 (7)

From Eq. 6, σ_x and σ_y can be solved as:

 , 

When σ_y = 0, it was determined that –ε_y/ε_x = µ. In other words, the absolute value of the ratio between the linear strains ε_y and ε_x at the position of σ_y = 0 is the Poisson’s ratio of the material.

Dynamic and static stress and strain of cantilever plates made of steel, aluminum and glass was calculated by ANSYS. Input material constants are as followed:

Steel: E=200 GPa, µ=0.30, ρ=7800 kg/m³;

Aluminum: E=69 GPa, µ=0.34, ρ=2700 kg/m³;

Glass: E=55 GPa, µ=0.25, ρ=2500 kg/m³.

In ANSYS calculation, “Shell 63” element was used in meshing with 50 × 10 to compute for dynamic and static stress and strain of cantilever plate specimen with l/b of 6, 5, 4 and 3.

Positions to paste strain rosette for measurement of Poisson’s ratio of steel, aluminum and glass are shown in Table 9 and 10.

Table 9. Position of the Strain Rosette Pasted for Measuring the Dynamic Poisson’s Ratio of a Cantilever Plate x/l

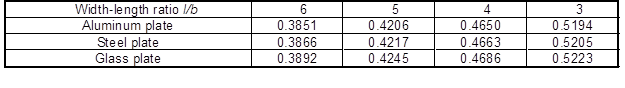
Table 10. Position of the Strain Rosette Pasted for Measuring the Static Poisson’s Ratio of a Cantilever Plate x/l

Based on the data for the steel cantilever plates in Tables 8 and 9, the positions of the strain rosette pasted for measuring the dynamic and static Poisson’s ratios were expressed in Eqs. 8 and 9, respectively:

x/l = 0.7387 – 0.0869l/b + 0.0047l²/b² (8)

(r = 0.99999, n = 4, l/b = 3, 4, 5 and 6)

x/l = 0.6291 – 0.0134l/b + 6 × 10^-4l²/b² (9)

(r = 1, n = 4, l/b = 36)

Equations 8 and 9 were obtained based on the data for steel. However, considering the data in Tables 8 and 9 and the Poisson’s ratios of rolled aluminum and pure copper, this test can also be applied to isotropic materials.

Future Directions

In this work, the Poisson’s ratio of the material was dynamically measured based on the stress-strain analysis of the first-order bending mode of the cantilever plate. In fact, in this work, the elastic modulus of tested materials can be also calculated by the testing result of the first-order bending frequency. Based on the results from this paper, we plan to carry out the research work of simultaneously measuring the elastic modulus, shear modulus, and Poisson’s ratio of materials in our future work. Besides, in the future, ideas in this study are also expected to be used in dynamic measurement and analysis of the elastic constants of novel materials such as FGM and nanowires, in order to improve the assessment level of mechanical properties of these materials and establish the evaluation standard. We expect to make more contributions to the application of novel materials in various fields such as civil engineering, aerospace engineering, biomedical engineering, mechanical engineering, optics, electromagnetism, chemistry, nuclear energy, and information.

CONCLUSIONS

1. In the first-order bending vibration of the timber cantilever plate, the absolute value of the ratio between the transverse (ε_y) and longitudinal strains (ε_x) increased with the increase in distance to the cantilever end (x); however, when x increased, the absolute value of the ratio between the transverse stress (σ_y) and longitudinal stress (σ_x) decreased from a positive to a negative value. Thus, there was a position where the transverse stress (σ_y) was equal to zero. At this position, the absolute value of the ratio between the transverse (ε_y) and longitudinal strains (ε_x) is the Poisson’s ratio of the material.
2. For timber, the ratio of transverse stress to longitudinal stress was very low within the entire cantilever plate. For example, the maximum ratio was 0.043 for beech and approximately 0.02 for balsa, spruce, Scots pine, and ash. The characteristics of stress distribution in the timber cantilever plate are different from those in isotropic materials, such as low-carbon steel and aluminum. Although the ratio of transverse stress to longitudinal stress in timber was very low within the entire cantilever plate, there was a significant difference in elastic modulus between the main directions of timber. Therefore, such a ratio should not be ignored when measuring Poisson’s ratio.
3. In the dynamic measurement of the Poisson’s ratio of timber, the cross strain rosette should be pasted at the position where the transverse stress (σ_y) is equal to zero. For the tangential-section cantilever plate, the pasting position of the cross strain rosette had a relationship with the width-to-length ratio and density of the plate, while for the radial-section and transverse-section cantilever plate, the pasting position of the cross strain rosette was only affected by the length-to-width ratio.
4. The accuracy of the measurements of the dynamic Poisson’s ratio of timber was verified by axial tension and four-point bending tests.
5. In the first-order bending vibration of the cantilever plate made of isotropic materials, there also existed a position where the transverse stress (σ_y) was equal to zero. Thus, the position of the cross strain rosette was only affected by the length-to-width ratio. The accuracy of the measurements of the dynamic Poisson’s ratio of steel, rolled aluminum, and pure copper was verified by axial tension and static tests.

ACKNOWLEDGEMENTS

This study was funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), the Special Scientific Funding Program for North Jiangsu (BN2015143), and the Undergraduate Training Program for Innovation of Jiangsu Province (201510298111X).

REFERENCES CITED

Bouderba, B., Houari, M. S. A., and Tounsi, A. (2013). “Thermomechanical bending response of FGM thick plates resting on Winkler–Pasternak elastic foundations,” Steel and Composite Structures 14(1), 85-104. DOI:10.12989/scs.2013.14.1.085

Brancheriau, L., and Bailleres, H. (2002). “Natural vibration analysis of clear wooden beams: A theoretical review,” Wood Science and Technology 36(3), 347-365. DOI: 10.1007/s00226-002-0143-7

Fu, Z. F. (2002). Textbook of Modal Analysis of Vibration and Parameter Identification, Chinese Machine Press, Beijing, China.

Hebali, H., Tounsi, A., Houari, M. S. A., Bessaim, A., and Adda Bedia, E. A. (2014), “A new quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates,” ASCE J. Engineering Mechanics 140, 374-383. DOI: 10.1061/(ASCE)EM.1943-7889.0000665

Liu, H. W. (1983). Textbook of Material Mechanics,Higher Education Press, Beijing, China.Ma, G. X. (1996). “Dynamic (static) measurement of the elastic constants in uniaxially-reinforced composite sheet,” Acta Materiae Compositae Sinica13(2), 117-123.

Sun, Y. F. (1999). Textbook of Lumber Manufacturing Technology, China Forestry Press, Beijing, China.Tan, S. X., and Zhou, D. G. (2007). Wood Industry Handbook, China Forestry Press, Beijing, China.

Wang, Z. (2007). “Dynamic measurement of elastic modulus and damping ratio of HDF and OSB,” Journal of Nanjing Forestry University, 31(3), 147-149.

Wang, Z., Gu, L. L., Gao, Z. Z., Liu, B., and Wang, Y. L. (2015). “Experimental study on Poisson’s ratio of lumber by dynamic testing,” Scientia Silvae Sinicae 51(5), 102-107.

Wang, Z., He, J. L., and Wang, X. D. (2008). “Test of natural frequency of woodworking band saw blade structure,” Journal of Vibration, Measurement & Diagnosis 28(2), 159-163.

Wang, Z., Li, L., and Gong, M. (2012). “Dynamic modulus of elasticity and damping ratio of wood-based composites using a cantilever beam vibration technique,” Construction & Building Materials 28(1), 831-834. DOI: 10.1016/j.conbuildmat.2011.09.001

Wang, Z. H., Gao, Z. Z., Wang, Y. L., Cao, Y, Wang, G. G., Liu, B and Wang, Z. (2015). “ A new dynamic testing method for elastic, shear modulus and Poisson’s ratio of concrete,” Construction & Building Materials 100, 129-135. DOI:10.1016/j.conbuildmat.2015.09.060

Article submitted: January 14, 2016; Peer review completed: March 18, 2016; Revised version received: April 1, 2016; Accepted: April 9, 2016; Published: May 5, 2016.

DOI: 10.15376/biores.11.3.5703-5721