Integration of Taguchi-Grey relational analysis technique in parameter process optimization for rice husk composite

Abstract

Injection molding is a widely used manufacturing process operation that generates polymer products. The selection of optimal injection molding process settings is essential due to the distinct influences of process parameters on polymeric material behavior and quality, particularly during the injection process. Therefore, it is vital to determine the optimized process parameters to enhance the mechanical properties of the products and ensure the most favorable performance. This paper examined the integration of Taguchi’s method with grey relational analysis (GRA) to determine the effects of varied injection molding parameters on the mechanical properties such as tensile strength and hardness values. The experiments were designed using Taguchi’s L9 orthogonal array after weighing in control factors, such as melting temperature, injection pressure, injection speed, and cooling time. The GRA revealed that the multiple responses correlation was successfully established. Finally, an analysis of variance was performed to validate the test outputs. The results revealed that the most influential factor was injection pressure, sequentially followed by melting temperature, cooling time, and injection speed.

Full Article

Integration of Taguchi-Grey Relational Analysis Technique in Parameter Process Optimization for Rice Husk Composite

Sity Ainy Nor Mohamed,^a,* Edi Syams Zainudin,^a,b S. M. Sapuan,^a,b Mohd Azaman Md. Deros,^c and Ahmad Mubarak Tajul Arifin ^d

Injection molding is a widely used manufacturing process operation that generates polymer products. The selection of optimal injection molding process settings is essential due to the distinct influences of process parameters on polymeric material behavior and quality, particularly during the injection process. Therefore, it is vital to determine the optimized process parameters to enhance the mechanical properties of the products and ensure the most favorable performance. This paper examined the integration of Taguchi’s method with grey relational analysis (GRA) to determine the effects of varied injection molding parameters on the mechanical properties such as tensile strength and hardness values. The experiments were designed using Taguchi’s L9 orthogonal array after weighing in control factors, such as melting temperature, injection pressure, injection speed, and cooling time. The GRA revealed that the multiple responses correlation was successfully established. Finally, an analysis of variance was performed to validate the test outputs. The results revealed that the most influential factor was injection pressure, sequentially followed by melting temperature, cooling time, and injection speed.

Keywords: Integration; Injection molding; Natural composite; Optimization

* Corresponding author: sityainy@gmail.com

INTRODUCTION

Based on recent developments in the manufacturing sector, plant fibers are being used as an amplifier in thermoset and thermoplastic products to replace synthetic materials. Such usage of plant fibers is particularly motivated by reductions in manufacturing costs, natural fiber capabilities to enhance the performance of engineering component applications, and concerns over environmental pollution due to disposal constraints (Sanjay et al. 2018). Therefore, cutting-edge research and development efforts have led to new products based on natural resources. Plant fibers, such as hemp, jute, flax, and kenaf, are the primary choices in generating plant fiber composites for various industry sectors (Lau et al. 2018).

Research on composites has shifted its focus to a variety of agricultural waste as fillers and reinforcements in composites; these include rice and wheat husks, as well as straw, bagasse, and corn stalks (Madurwar et al. 2013). Rice husk (RH) is an agricultural waste that has vast product advantages. During the rice milling process, approximately 78% of the outcome is identified as rice, broken rice, and bran. Meanwhile, the remaining 22% of the weight is identified as RH. Similar to other plant fibers, RH is a lignocellulosic fiber that is composed of cellulose (35%), hemicellulose (25%), and lignin (20%) (Arjmandi et al. 2017). However, RH is hydrophilic and absorbs moisture, which suggests a drawback in its mechanical properties. The combination of a hydrophobic thermoplastic matrix, such as polypropylene (PP), polyethylene, and polystyrene, produces a composite that has the strength of a fiber-matrix interface that enhances mechanical properties.

Natural fiber composites are derived from various manufacturing techniques, including press molding, extrusion, injection molding, compression molding, and resin transfer molding (Ho et al. 2012). To mass produce thermoplastic composites, injection molding is an easy and effective method. However, essential process parameters need to be optimized for ideal outcomes, such as injection speed, injection pressure, melting temperature, holding time, and cooling time (Muthuraj et al. 2016). Hence, investigations have been conducted to improve or optimize quality characteristics to generate high-quality commercial plastic products, apart from maximizing service capabilities for the products. Studies have omitted the interaction effects between the fixed parameters and the mechanical properties of the products, although these aspects may have substantial implications.

This paper describes the influence of optimizing the parameters involved in the injection molding process to obtain maximum performing mechanical properties (tensile, strength, and hardness) in the composite polymer. The method applied in this study refers to the integration between the Taguchi’s method and the grey relational analysis (GRA), which is a simultaneous optimization process of varied parameters to display the impacts of multiple reaction combinations on the mechanical properties of RH composites. The tested parameters were injection pressure, injection speed, melting temperature, and cooling time. The GRA results indicated that injection pressure had the dominant effect on the mechanical properties of RH composites, followed by the melting temperature, cooling time, and injection speed. Additionally, characterization via an analysis of variance (ANOVA) was performed in this study to verify the values obtained from the integrated Taguchi-GRA method.

THEORY

Taguchi Method

The Taguchi method has been widely applied in the engineering design sector. It is comprised of system design, parameter design, and tolerance design procedures to achieve a robust process and produce the best quality products (Mitra et al. 2016). The primary application of the Taguchi method is for parameter design, which refers to an engineering method to generate products or to devise a process design with the focus placed on optimizing the integral parameters to establish good quality production with minimal variation. The Taguchi design works as a dominant and efficient method to design processes that operate consistently and optimally in numerous situations. Table 1 presents the required number of experiments based on orthogonal array. This process devises a strategic set of required arrangements, apart from determining the best design.

Table 1. Orthogonal Array Selection (Karna and Sahai 2012)

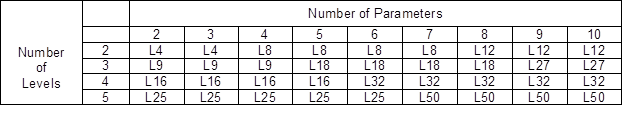
The Taguchi method employs a signal-noise (S/N) ratio as a quality feature. The S/N ratio refers to a measurable value in place of the standard deviation value. This is because when the mean value decreases, the standard deviation will most likely decrease as well and vice versa. Therefore, the quality characteristics are classified into three categories which are named “the larger the better”, “the smaller the better”, and “nominal is the best” (Lal and Vasudevan 2013).

Grey Relational Analysis (GRA)

The Grey system theory, which was initiated by Deng in 1982 (Raju et al. 2017), has been successfully applied in the engineering industry for prediction and control, as well as social, economic, and agricultural systems. In fact, the development and application of the Grey system theory is ongoing. The concept of GRA originated from the Grey system theory, which reflects a measurement method that determines the correlation between sequences using a certain amount of data. The GRA is based on geometrical mathematics in compliance with the principles of normality, symmetry, entirety, and proximity. The measure of relevance between two systems or two sequences can be defined as the relational grade that depicts the trend correlation between reference (objective sequence) and comparative sequences within a system (Prayogo and Lusi 2016). If both the reference and comparative sequences lean toward concordance, then the relational grade approaches one. In contrast, if the reference and comparative sequences do not lean toward concordance, then the relational grade approaches zero. In comparison to conventional statistical procedures, GRA only requires small amounts of data and the data are not limited to a certain statistical distribution. Generally, GRA gives desirable information on the similarity among sequences. The following equations (Eqs. 4 to 7) present the GRA algorithm.

Data Pre-processing for Normalized Values

The data pre-processing step is essential in GRA because the range and unit in a data sequence may vary from the rest. This step is also necessary when the range of sequence scatter is too large, or when the target direction in the sequence differs. This data pre-processing step refers to a process of transferring the original sequence to one that is comparable (Sreenivasulu and Rao 2012; Ali et al. 2018). Thus, the experimental outputs are normalized in a range between zero and one. The original sequence, and the first characteristic, “the larger, the better,” is shown in Eq. 4,

where (k) and xi(k) refer to the sequence after data pre-processing and the comparability sequence, respectively, and k = 1 for i = 1, 2, 3, … for experiment numbers 1 to 9. The deviation sequence of the reference sequence and the comparability sequence (k) can be calculated using Eq. 5:

Computing the Grey Relational Coefficient (GRC) and Grey Relational Grade (GRG)

The correlation between the ideal and the actual normalized experimental outputs can be expressed via the GRC and the GRG. The GRC is defined in Eq. 6,

where denotes the deviation sequence of the reference sequence, , and the comparability sequence is for the identification coefficient, which is fixed at 0.5.

After obtaining the GRC, the GRG is computed by averaging the GRC corresponding to each performance characteristic. The overall evaluation of the multiple performance characteristics is based on the GRG, as presented in Eq. 7,

where yi refers to the GRG for the ith experiment, while n reflects the number of performance characteristics. Therefore, a higher GRG showed that the corresponding experimental result was closer to the ideally normalized value.

Validation Test Using ANOVA

The main purpose of an ANOVA is to evaluate experimental error (Sufiyanto 2017). In the Taguchi method, the interaction between factors has been regarded as part of the experimental error. A factor effect is considered meaningful when its value exceeds the experimental error. Based on this method, a process adjustment approach in optimizing parameter sets or process specifications is applied after considering a particular limit and maintaining the other factors. The main objective of this method is to reduce cost and enhance efficiency. In fact, this approach is a quantitative technique related to making decisions, especially within the manufacturing industry (Shivapragash et al. 2013). Studies have attempted to associate process parameters with the mechanical properties of polymers. During the injection molding process, the fiber orientation varied substantially across mold thicknesses, hence causing the polymer to be anisotropic, which affected the main features of the product. However, the mechanical properties of the product can be improvised by determining the fiber orientation during the injection process. In addition, the impacts of various parameters, such as the melt and mold temperatures, flow rate, matrix, fiber properties, volume fraction of fibers, molding geometry, gate type, and gate location, on detailed distribution and fiber orientation in the final product have been investigated (Graupner et al. 2016).

The fabrication of polymer products through injection molding processes is similar to the Taguchi method for optimizing process parameters. The effects of integral processing parameters, such as injection velocity, packing pressure, mold and melt temperatures, and cooling time, on the mechanical properties and failure behavior of the polymer have been thoroughly examined (Kc et al. 2016). Based on the observation of the polycarbonate (PC) polymer study, the mold and melt temperatures display considerable impacts when compared to other parameters. The combination of higher mold temperatures with moderate melt temperatures decreases the viscosity of PC while increasing the flow speed in the molds. As a result, more organized molecular orientation and stronger molecular bonds can be generated (Dar et al. 2017), resulting in an improvement of the mechanical properties. Studies investigated optimizing the shrinkage and warpage impacts on polymer products. Numerous approaches have been proposed to address this problem. The review by Radhwan et al. (2015) states that the most important parameters that may affect the shrinkage and warpage are melt temperature, packing time, mold temperature, and packing pressure.

Kumar et al. (2014) applied the Taguchi method to determine the mechanical properties of epoxy-based wood dust composites. Optimization of the three varied tensile speed tests was performed. The main factor that affected both the load and tensile strength values was speed, in which higher speeds led to shorter time for the filler to become oriented. In contrast, the bending stress was only influenced by the filler content in the composite. The bending involved load action on the material thickness. The Taguchi method was also employed for parameter design to identify the optimum surface roughness performance on the aluminum material with cutting parameters of depth of cut, cutting speed, feed rate, and tool diameter (Razavykia et al. 2015). As a result, the tool diameter was an irrelevant cutting factor for surface roughness. In another study, the Taguchi method was combined with ANOVA to correlate the cutting speed and feed rate with delamination in a composite laminate (Sreenivasulu and Rao 2013). Prayogo and Lusi (2016) used the GRA to evaluate the current, pulse on time, pulse off time, and discharging time as the electrical discharge machining (EDM) process parameters with the aim of minimizing material removal rate and overcut.

The optimization method is important to determine the ideal mechanical properties of composite materials by using efficient, precise, and robust experimental layout approaches with adequate orthogonal array. However, some aspects must be considered, in particular, parameter design and optimum condition (optimum level for each parameter). Additionally, this method saves time and money, as the number of experiments can be minimized when compared to conventional approaches. The Taguchi method has been widely applied to determine the influential factors that dictate the quality characteristics in the manufacturing process. The combination of the Taguchi method with another optimization technique appears to be effective in investigating the impacts of multiple factors on performance, aside from identifying the factors that exert more influence than the rest.

EXPERIMENTAL

Materials

The RH-PP pellet preparation was performed via an extrusion process with a compatibilizer agent. A 35 wt% filler loading was designed for this study. The RH fibers with sizes ranging between 100 µm and 500 µm were used as the filler content with Struktol TR016 (Rhetech, Whitmore Lake, MI, USA) as the compatibilizer agent. The compatibilizer agent functioned as an effective binder with good adhesion. It is important for polymers to have filler content with uniform blending to maintain their physical properties (Borůvka et al. 2015). Its low molecular weight reduced the viscosity during the process, hence enhancing flow characteristics. The PP with 0.90 gm/cm3 to 0.91 gm/cm3 gravity (Polypropylene Malaysia Sdn Bhd, Pahang, Malaysia) was selected as the polymer matrix because it is environmentally friendly, cost-effective, and fulfills technical requirement.

Methods

Mixing and processing

In this study, the RH-PP composites were prepared via an injection molding technique at the SIRIM Green Laboratory, Shah Alam (Selangor, Malaysia). Experimental ground RH was dried at 105 °C in an air dryer oven for 24 h to expel any moisture trapped to a content of 1% to 2%, and then stored over desiccant in a sealed container. The RH was then mixed with PP using a tumbler mixer for better dispersion of the RH and PP. Later, the mixed compounds were melt-blended with a twin-screw extruder (ZE-25; KraussMaffei Berstorff, Munich, Germany) at 160 °C and 190 °C for the feed zone and die zone, respectively. The twin-screw extruder was a co-rotating type (L/D ratio = 33). The compounds were extruded and pelletized at 100 rpm screw speed. The pellets were stored in a sealed container and dried for approximately 3 h to 4 h before being injection-molded. The temperatures applied for injection-molded samples were 170 °C and 190 °C for the feed zone and die zone, respectively. The samples were injected at an injection pressure between 45 kg/m2 and 50 kg/m2 with a 30 s cooling time. At the end of the procedure, composites with varied filler loading composed of RH, PP, and a coupling agent were prepared.

Specimen preparation

After the extrusion process, the pellets were injected using a 60-tonne Haitian MA600 II/130 machine (Haitan Precision, Ningbo, China) (Fig. 1) into the shape shown in Fig. 2 based on the test standard ASTM D638-03 (2004). The experiments were run at the National Energy University laboratory located at Selangor, Malaysia.

Fig. 1. 60-tonne injection molding machine

Fig. 2. Test specimen

Process parameters (e.g., injection pressure and speed, melt and mold temperatures, cooling and holding time, and holding pressure) can strongly affect the mechanical properties, such as tensile strength and hardness (Gaaz et al. 2016). In this optimization process, three different levels were employed to determine four notable molding parameters that affected the tensile strength and hardness values, which were melting temperature, injection pressure, injection speed, and cooling time, as presented in Table 2 (Ibrahim et al. 2014). These parameters were chosen based on the machine setting capabilities. The design parameters combination (orthogonal array) was integrated to increase the experimental efficiency. The arrangements of the experimental runs for the L9 orthogonal array are displayed in Table 3.

Table 2. Factors and Levels Selection

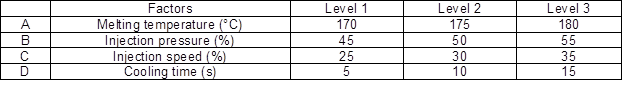
Table 3. Values of Orthogonal Array (Vignesh et al. 2016)

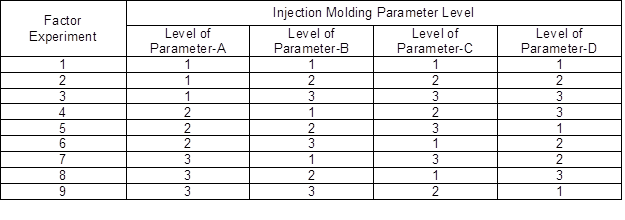
Methods

Tensile test

Mechanical tests have an important role in evaluating the fundamental nature of engineering materials. This aspect is essential in generating new materials with controlled material quality for use in designing and constructing sectors. Furthermore, it is important to determine the strength of a material to bear the burden placed on the material. As such, tensile tests were conducted by adhering to the ASTM D638-03 (2004) standard using a universal testing machine (Instron 3365; Instron Malaysia, Selangor, Malaysia), as illustrated in Fig. 3. Dog bone-shaped geometry specimens were tested at a crosshead speed of 5 mm/min to maintain a constant stress rate and a gauge length of 80 mm. Additionally, an extensometer device was employed to measure its elongation during the tests. The specimens were tested in each experimental run based on the orthogonal array arrangement.

Fig. 3. Tensile machine, Instron 3365

Fig. 4. The specimen placed on the Rockwell hardness machine

Hardness test

Hardness tests were conducted using a Rockwell hardness tester (Yakin Maju, Jakarta, Indonesia). The specimens were carefully placed on the machine, as portrayed in Fig. 4. The tests adhered to test standard ASTM D785-08 (2008) and were recorded based on the R scale. During the experiments, 0.5 in (12.7 mm) bends were applied with a major load fixed at 60 kg. The pointer was rotated clockwise until the pointer tip touched the surface of the specimen. This experiment was held for 30 s until the machine screen displayed the specimen hardness readings. The experiments were repeated at various spots on the specimens to obtain the mean value of the hardness aspect. The Rockwell experiments were performed mainly because the accuracy of hardness readings can be obtained directly via machine display, hence dismissing special preparation on various specimens.

RESULTS AND DISCUSSION

The Taguchi method introduced the assessment of the S/N ratio to measure the quality characteristic used in the process of optimizing injection molding parameters. The best tensile strength and hardness values were retrieved and the acquired values​​ from the experiments are tabulated in Table 4. The main reason for calculating the S/N ratio was to evaluate the impacts of design parameter changes upon the composite mechanical properties of both responses. Both responses represented the optimum level of the set of changes that occurred. In this experiment, “the larger, the better” characteristic was selected as the reference level in calculating the S/N ratio values. This characteristic represented a smaller variation of both response values and a smaller error, which gave the quality characteristic and target value higher consistency (Kuo et al. 2015). Table 4 shows that the best parameter set combination was determined by the level that contributed to the highest value for each factor. The highest tensile strength value was obtained during the 7th experiment (A3, B1, C3, and D2), while the highest hardness value was retrieved at the 5th experiment (A2, B2, C3, and D1).

Table 4. Responses for the Experimental Sets and S/N Ratios

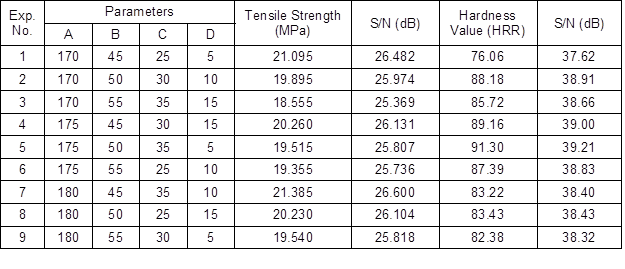
In general, the GRA is applied to measure the correlation level between sequences through the GRG value. Based on the GRA application with the Taguchi method, the optimization of various reaction characteristics was converted to single feature optimization, in which the GRG was considered an objective function (Puh et al. 2016). Tables 5 and 6 present the steps of pre-processing raw data towards normalizing S/N ratios using Eqs. 1 and 3. This pre-processing stage was performed to prevent the effects of varied unit (non-dimension) uses, as well as to minimize the aspect of variability due to the diverse factors that had been considered (Raghuraman et al. 2013).

Table 5. Data Pre-processing for Normalized S/N Ratio Values

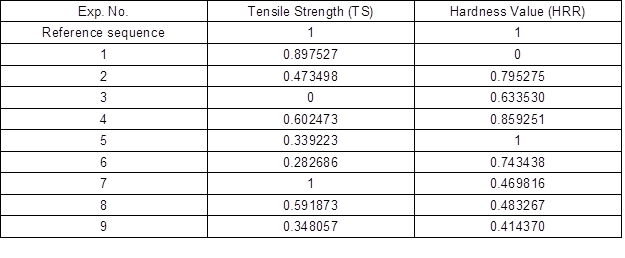
Table 6. Deviation Sequence

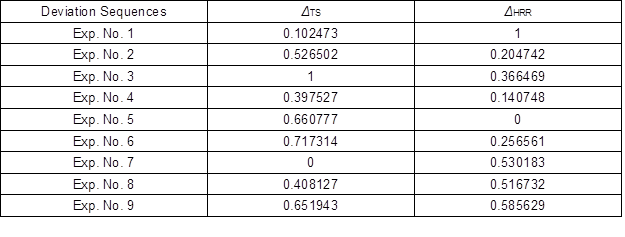
Based on the normalized experimental data, the GRC was calculated using Eq. 3. This was performed to select “the larger, the better” category that reflected the correlation between the desired test data and the actual data. Next, the GRG was calculated using Eq. 4, which refers to the average corresponding to each feature performance. Hence, a combination of optimal process parameters was rated based on the highest GRG via the Taguchi method. Both the GRC and GRG values ​​are displayed in Table 7. The values that exceeded the GRG represented stronger levels of correlations between the referral and given sequences. The referral sequence was the best process response obtained from the experimental arrangement. The highest GRG value was obtained at the 7th sequence of the experiment, which signified that the experiment sequence at this level was closer to the desired optimum value. In contrast, the optimum parameters were determined based on the GRG presented in Table 8. This study revealed that injection pressure, followed by melting temperature, injection speed, and cooling time had the most substantial impacts on tensile strength and hardness. Overall, these experiments suggested that the optimization of multiple reaction processes can be converted into a single coefficient optimization.

Table 7. GRC and GRG Values

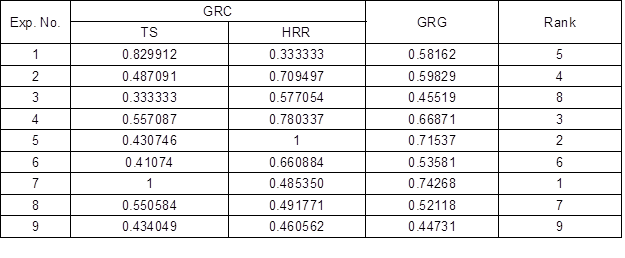
Table 8. Responses for GRG

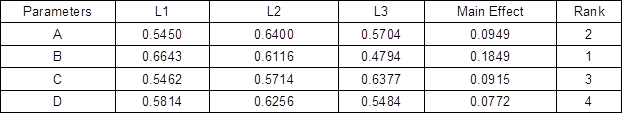
Table 9 summarizes the outcomes obtained from the ANOVA analysis. The ANOVA analysis determined the parameters that gave the most substantial impact on the performance characteristic. The injection pressure exhibited the highest percentage of contribution (59.59%), followed by the melting temperature (15.87%), injection speed (14.68%), and lastly the cooling time (9.86%). Based on the combination of the Taguchi-Grey method, the optimal parameters identified were the melting temperature at 2nd level, injection pressure at 1st level, injection speed at 3rd level, and cooling time at 2nd level, as showcased in Fig. 5.

Table 9. ANOVA for Responses

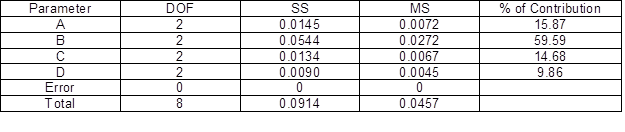
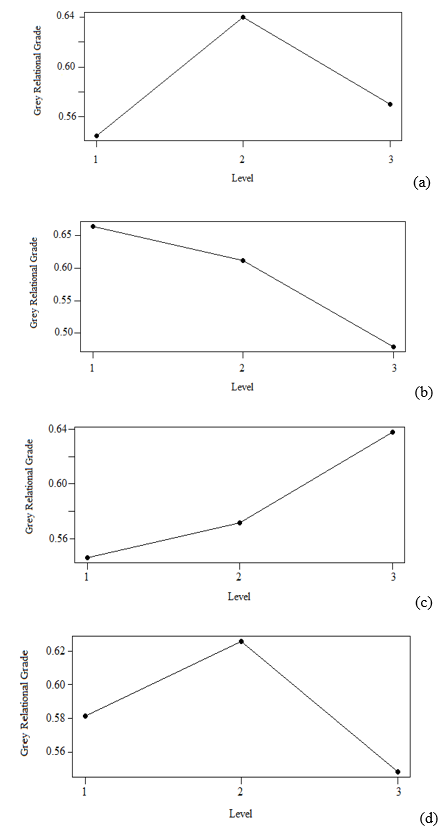
Fig. 5. Control factor of GRG response values for: a) melting temperature, b) injection pressure, c) injection speed, and d) cooling time

Studies have investigated the formation of core structures in injection molding products. Mechanical properties reflect the mechanical structure of a product resulting from the effects controlled by molecular orientation, free volume, chemical nature, and molecular weight. During the injection process, the outer layer of the product structure is exposed to high pressure, tensile stress, and a substantial cooling rate, which affects various structural core morphologies that constitute the mechanical properties of the product. Meanwhile, the outer core structure is influenced by the melting temperature and injection pressure (Kuzmanović et al. 2016). Increments in temperature during this process further reduce molecular orientation, which causes a decrease in both the strain and enthalpy of cold crystallization. When the injection pressure reaches a certain point, the density of the product drastically increases, which results in low porosity and a more compacted structure (Hu 2016).

It is important for the specified parameter value for the injection speed to be adequate. The molten material should completely fill the cavity, both rapidly and efficiently, to hinder glitches while removing the component from the mold (Raos and Stojsic 2014). In contrast to the listed effects, low injection speed results in larger temperature variations between the parts near the gate and those at a further distance. This happens because the molten material starts to cool while the mold is still being filled (Kuram et al. 2014). Cold molten material has higher viscosity and demands higher injection pressure to generate a good quality product. Consequently, the strength of the product’s properties increases when the molecular movement is increased.

The semicrystalline polymers are composed of multi-layer configurations (e.g., skin-core), mainly due to the presence of high-pressure fields and cooling rates imposed during the processing stages. The crystallized polymer generates a typical configuration layer that consists of an amorphous and oriented fiber dispersion in the skin layer, an intermediate shear crystallized layer, and an internal amorphous core (O’Dowd et al. 2006). The diversity of these structural layers signifies the importance of crystallization due to the shear stress that occurs during the injection process (Liparoti et al. 2017). In conclusion, the composite polymer morphology highly relied on the rate of cooling time and shear stress imposed during the processing stages because the cooling rate has a notable influence on the crystallinity (Suplicz et al. 2013).

CONCLUSIONS

In this study, the Grey relational analysis (GRA), which served as the multi-criteria optimization technique, was applied to optimize the injection molding parameters to exert an effect on the mechanical properties of natural fiber composites. Conclusions are as follows:

The combination of GRA based on the response table derived from the Taguchi method successfully assessed the feasibility of each process parameter in injection molding towards the mechanical properties of RH composites.
The multiple responses performance characteristic was converted to an optimization of a single performance characteristic from the stance of the correlations between melting temperature, injection pressure, injection speed, and cooling time to obtain enhanced outcomes for the tensile strength and hardness properties.
The optimal combination revealed that the injection pressure generated the highest percentage of the most affected parameter for injection molding process (59.6%), while melting temperature gave 15.9%, injection speed was 14.7%, and cooling time was 9.9%.

ACKNOWLEDGMENTS

The present work is supported by research grant UPM/700-2/1/GP-IPS/2017/9538700 and the Ministry of Higher Education.

REFERENCES CITED

Ali, M. A. M., Idayu, N., Izamshah, R., Kasim, M. S., Salleh, M. S., and Sivarao. (2018). “Multi objective optimization of injection moulding process parameters on mechanical properties using Taguchi method and grey relational analysis,” International Journal of Engineering & Technology 7(3.7), 14-16. DOI: 10.14419/ijet.v7i3.7.16196.

Arjmandi, R., Hassan, A., and Zakaria, Z. (2017). “Rice husk and kenaf fiber reinforced polypropylene biocomposites,” in: Lignocellulosic Fibre and Biomass-Based Composite Materials, M. Jawaid (ed.), Woodhead Publishing Ltd., Cambridge, UK, 77-94. DOI: 10.1016/B978-0-08-100959-8.00005-6

ASTM D638-03 (2004). “Standard test method for tensile properties of plastics,” ASTM International, West Conshohocken, PA.

ASTM D785-08 (2008). “Standard test method for Rockwell hardness of plastics and electrical insulating materials,” ASTM International, West Conshohocken, PA.

Borůvka, V., Zeidler, A., and Holeček, T. (2015). “Comparison of stiffness and strength properties of untreated and heat-treated wood of Douglas fir and alder,” BioResources 10(4), 8281-8294. DOI: 10.15376/biores.10.4.8281-8294

Dar, U. A., Xu, Y. J., Zakir, S. M., and Saeed, M. U. (2017). “The effect of injection molding process parameters on mechanical and fracture behavior of polycarbonate polymer,” Journal of Applied Polymer Science 134(7), Article ID 44474. DOI: 10.1002/app.44474

Gaaz, T. S., Sulong, A. B., Kadhum, A. A. H., Nassir, M. H., and Al-Amiery, A. A. (2016). “Optimizing injection molding parameters of different halloysites type-reinforced thermoplastic polyurethane nanocomposites via Taguchi complemented with ANOVA,” Materials 9(11), 947-966. DOI: 10.3390/ma9110947

Graupner, N., Ziegmann, G., Wilde, F., Beckmann, F., and Müssig, J. (2016). “Procedural influences on compression and injection moulded cellulose fibre-reinforced polylactide (PLA) composites: Influence of fibre loading, fibre length, fibre orientation and voids,” Composites Part A: Applied Science and Manufacturing 81, 158-171. DOI: 10.1016/j.compositesa.2015.10.040

Ho, M. P., Wang, H., Lee, J. H., Ho, C. K., Lau, K. T., Leng, J., and Hui, D. (2012). “Critical factors on manufacturing processes of natural fibre composites,” Composites Part B: Engineering 43(8), 3549-3562. DOI: 10.1016/j.compositesb.2011.10.001

Hu, Z. (2016). “Injection parameters optimization and artificial aging of automotive die cast aluminum alloy,” Materials and Manufacturing Processes 31(6), 787-793. DOI: 10.1080/10426914.2015.1004706

Ibrahim, M. H. I., Zainol, M. Z., Othman, M. H., Amin, A. M., Asmawi, R., and Sa’ude, N. (2014). “Optimisation of processing condition using Taguchi method on strength of HDPE-natural fibres micro composite,” Applied Mechanics and Materials 660, 33-37. DOI: 10.4028/www.scientific.net/AMM.660.33

Karna, S. K., and Sahai, R. (2012). “An overview on Taguchi method,” International Journal of Engineering and Mathematical Sciences 1(1), 1-7.

Kc, B., Faruk, O., Agnelli, J. A. M., Leao, A. L., Tjong, J., and Sain, M. (2016). “Sisal-glass fiber hybrid biocomposite: Optimization of injection molding parameters using Taguchi method for reducing shrinkage,” Composites Part A: Applied Science and Manufacturing 83, 152-159. DOI: 10.1016/j.compositesa.2015.10.034

Kumar, R., Kumar, K., and Bhowmik, S. (2014). “Optimization of mechanical properties of epoxy based wood dust reinforced green composite using Taguchi method,” Procedia Materials Science 5, 688-696. DOI: 10.1016/j.mspro.2014.07.316

Kuo, C. F. J., Lan, W. L., Chen, C. Y., and Tsai, H. C. (2015). “Property modification and process parameter optimization design of polylactic acid composite materials. Part I: Polylactic acid toughening and photo-degradation modification and optimized parameter design,” Textile Research Journal 85(1), 13-25. DOI: 10.1177/0040517514540766

Kuram, E., Timur, G., Ozcelik, B., and Yilmaz, F. (2014). “Influences of injection conditions on strength properties of recycled and virgin PBT/PC/ABS,” Materials and Manufacturing Processes 29(10), 1260-1268. DOI: 10.1080/10426914.2014.941481

Kuzmanović, M., Delva, L., Cardon, L., and Ragaert, K. (2016). “The effect of injection molding temperature on the morphology and mechanical properties of PP/PET blends and microfibrillar composites,” Polymers 8(10), 355-371 DOI: 10.3390/polym8100355

Lal, S. K., and Vasudevan, H. (2013). “Optimization of injection moulding process parameters in the moulding of low density polyethylene (LDPE),” International Journal of Engineering Research and Development 7(5), 35-39.

Lau, K. T., Hung, P. Y., Zhu, M. H. and Hui, D. (2018). “Properties of natural fibre composites for structural engineering applications,” Composites Part B: Engineering 136, 222-233. DOI: 10.1016/j.compositesb.2017.10.038

Liparoti, S., Speranza, V., Sorrentino, A., and Titomanlio, G. (2017). “Mechanical properties distribution within polypropylene injection molded samples: Effect of mold temperature under uneven thermal conditions,” Polymers 9(11), 585-602. DOI: 10.3390/polym9110585

Madurwar, M. V., Ralegaonkar, R. V., and Mandavgane, S. A. (2013). “Application of agro-waste for sustainable construction materials: A review,” Construction and Building Materials 38, 872-878. DOI: 10.1016/j.conbuildmat.2012.09.011

Mitra, A. C., Jawarkar, M., Soni, T., and Kiranchand, G. R. (2016). “Implementation of Taguchi method for robust suspension design,” Procedia Engineering 144, 77-84. DOI: 10.1016/j.proeng.2016.05.009

Muthuraj, R., Misra, M., Defersha, F., and Mohanty, A. K. (2016). “Influence of processing parameters on the impact strength of biocomposites: A statistical approach,” Composites Part A: Applied Science and Manufacturing 83, 120-129. DOI: 10.1016/j.compositesa.2015.09.003

O’Dowd, F., Levesque, M., and Gilchrist, M. D. (2006). “Analysis of fibre orientation effects on injection moulded components,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture 220(12), 1909-1921. DOI: 10.1243/09544054JEM332

Prayogo, G. S., and Lusi, N. (2016). “Application of Taguchi technique coupled with grey relational analysis for multiple performance characteristics optimization of EDM parameters on ST 42 steel,” in: AIP Conference Proceedings 1725(1), 020061(1)-020061(7). DOI: 10.1063/1.4945515

Puh, F., Jurkovic, Z., Perinic, M., Brezocnik, M., and Buljan, S. (2016). “Optimization of machining parameters for turning operation with multiple quality characteristics using Grey relational analysis,” Tehnički Vjesnik 23(2), 377-382. DOI: 10.17559/TV-20150526131717

Radhwan, H., Mustaffa, M. T., Annuar, A. F., Azmi, H., Zakaria, M. Z., and Khalil, A. N. M. (2015). “An optimization of shrinkage in injection molding parts by using Taguchi method,” Journal of Advanced Research in Applied Mechanics 10(1), 1-8.

Raghuraman, S., Thiruppathi, K., Panneerselvam, T., and Santosh, S. (2013). “Optimization of EDM parameters using Taguchi method and Grey relational analysis for mild steel IS 2026,” International Journal of Innovative Research in Science, Engineering and Technology 2(7), 3095-3104.

Raju, B. S., Sekhar, U. C., and Drakshayani, D. N. (2017). “Grey relational analysis coupled with principal component analysis for optimization of stereolithography process to enhance part quality,” in: IOP Conference Series: Materials Science and Engineering 225(1), 012228(1)-012228(13).

Raos, P., and Stojsic, J. (2014). “Influence of injection moulding parameters on tensile strength of injection moulded part,” Journal of Manufacturing and Industrial Engineering 13(3-4), 1-3. DOI: 10.12776/mie.v13i3-4.412

Razavykia, A., Yusof, N. M., and Yavari, M. R. (2015). “Determining the effects of machining parameters and modifier on surface roughness in dry turning of Al-20% Mg2Si-PMMC using design of experiments (DOE),” Procedia Manufacturing 2, 280-285. DOI: 10.1016/j.promfg.2015.07.049

Sanjay, M. R., Madhu, P., Jawaid, M., Senthamaraikannan, P., Senthil, S., and Pradeep, S. (2018). “Characterization and properties of natural fiber polymer composites: A comprehensive review,” Journal of Cleaner Production 172, 566-581. DOI: 10.1016/j.jclepro.2017.10.101

Shivapragash, B., Chandrasekaran, K., Parthasarathy, C., and Samuel, M. (2013). “Multiple response optimizations in drilling using Taguchi and Grey relational analysis,” International Journal of Modern Engineering Research 3(2), 765-768. DOI: 10.1.1.300.5681

Sufiyanto, S. (2017). “Optimization of injection molding parameters using the Taguchi method to maximize biocomposite material tensile strength,” Journal Teknik Mesin 7(2), 81-87.

Sreenivasulu, R., and Rao, C. S. (2012). “Application of Grey relational analysis for surface roughness and roundness error in drilling of Al 6061 alloy,” International Journal of Lean Thinking 3(2), 67-78.

Sreenivasulu, R., and Rao, C. S. (2013). “Design of experiments based Grey relational analysis in various machining processes – A review,” Research Journal of Engineering Sciences 2(1), 9472(21)-9472(26).

Suplicz, A., Szabo, F., and Kovacs, J. G. (2013). “Injection molding of ceramic filled polypropylene: The effect of thermal conductivity and cooling rate on crystallinity,” Thermochimica Acta 574, 145-150. DOI: 10.1016/j.tca.2013.10.005

Vignesh, K., Ramasivam, G., Natarajan, U., and Srinivasan, C. (2016). “Optimization of process parameters to enhance the mechanical properties of bone powder and coir fiber reinforced polyester composites by Taguchi method,” APRN Journal of Engineering and Applied Sciences 11(2), 1224-1231.

Article submitted: October 5, 2018; Peer review completed: November 26, 2018; Revised version received and accepted: November 27, 2018; Published: December 13, 2018.

DOI: 10.15376/biores.14.1.1110-1126